Technology and Investment
Vol.1 No.2(2010), Article ID:1764,8 pages DOI:10.4236/ti.2010.12016
Discrete Time Markov Reward Processes a Motor Car Insurance Example*
1Università “G. D’Annunzio” di Chieti, Dip. di Scienze del Farmaco, via dei Vestini, Chieti, Italy
2Jacan &, EURIA, Université de Bretagne Occidentale, 6 avenue le Gorgeu, Brest, France
3Università “La Sapienza”, Dip. di Matematica per le Decisioni Economiche, Finanziarie ed Assicurative, via del Castro Laurenziano, Roma, Italy
E-mail: g.damico@unich.it, jacques.janssen@skynet.be, raimondo.manca@uniroma1.it
Received December 11, 2009; revised December 20, 2009; accepted December 22, 2009
Keywords: Markov rewards processes, higher order moments, bonus-malus systems
Abstract
In this paper, a full treatment of homogeneous discrete time Markov reward processes is presented. The higher order moments of the homogeneous reward process are determined. In the last part of the paper, an application to the bonus-malus car insurance is presented. The application was constructed using real data.
1. Introduction
In the sixties and seventies, Markov reward processes were developed, mainly in the engineering fields in discrete and continuous time [1]. In [2] an application of Continuous Time Markov Reward Processes in life insurance was presented.
In this paper, we present the Discrete Time Markov Reward Processes (DTMRWP) as given in [3]. The evolution equation of the expected value of the DTMRWP is presented with different reward structures. Furthermore, the relations useful for the computation of the higher order moments of the Markov reward process are presented and they are given in matrix form too. To the authors’ knowledge, it is the first time that higher moments of a discrete time Markov reward process and the matrix approach for the first n moments are given. The matrix approach facilitates the algorithm construction as for example it is explained in [4] for semi-Markov reward processes.
We believe that DTMRWP can describe any kind of premiums or benefits involved in a generic insurance contract then they represent tool to approach in a general way actuarial problems.
In the last section an example on the application of DTMRWP in the motor car insurance is given using real data applied to the bonus-malus Italian rules.
2. Reward Structure, Classifications and Notation
The association of a sum of money to a state of the system and to a state transition assumes great relevance in the study of financial phenomena. This can be done by linking a reward structure to a stochastic process. This structure can be thought of as a function associated with the state occupancies and transitions [1].
In this paper the rewards are considered as amounts of money. These amounts can be positive, if they are benefits for the system and negative if they are costs.
A classification scheme of different kinds of DTM RWP is reported in [5] page 150.
2.1. Discounting Factors
The following notations will be used:
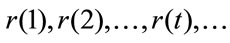 , for the discrete time homogeneous interest rates and
, for the discrete time homogeneous interest rates and
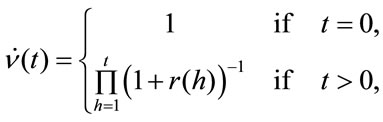 for the discrete time discount factors.
for the discrete time discount factors.
See [6] or [7] for further details on this topic.
2.2. Reward Notation
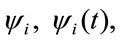 denote the reward that is given for the permanence in the i-th state; it is also called rate reward, see [8]; the first is paid in the cases in which the period amount in state i is constant in time, the second when the payment is a function of the state and the time of payment.
denote the reward that is given for the permanence in the i-th state; it is also called rate reward, see [8]; the first is paid in the cases in which the period amount in state i is constant in time, the second when the payment is a function of the state and the time of payment. 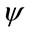 represents the vector of these rewards.
represents the vector of these rewards.
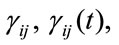 denote the reward that is given for the transition from the ith state to the jth one (impulse reward).
denote the reward that is given for the transition from the ith state to the jth one (impulse reward). 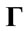 is the matrix of the transition rewards.
is the matrix of the transition rewards.
The different kinds of 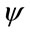 rewards represent an annuity that is paid because of remaining in a state. This flow is to be discounted at starting time. In the immediate case, the reward will be paid at the end of the period before the transition; in the due case the reward will be paid at the beginning of the period. On the other hand,
rewards represent an annuity that is paid because of remaining in a state. This flow is to be discounted at starting time. In the immediate case, the reward will be paid at the end of the period before the transition; in the due case the reward will be paid at the beginning of the period. On the other hand, 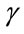 represents lump sums that are paid at the instant of transition. As far as the impulse reward
represents lump sums that are paid at the instant of transition. As far as the impulse reward 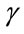 is concerned, it is only necessary to compute the present value of the lump sum paid at the moment of the related transition.
is concerned, it is only necessary to compute the present value of the lump sum paid at the moment of the related transition.
Reward structure can be considered a very general structure linked to the problem being studied. The reward process evolves together with the evolution of the Markov process which it is linked. When the studied stochastic system is in a state then a reward of type 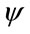 is paid; once there is a transition an impulse reward of
is paid; once there is a transition an impulse reward of 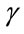 type is paid.
type is paid.
This behaviour is particularly efficient at constructing models which are useful to follow, for example, the dynamic evolution of insurance problems e.g. [9] and [10].
2.3. Matrix Operations
We give some matrix operation notation useful to describe the equations of the moments of the Markov reward processes in matrix form.
Given the two matrices A, B with the notations
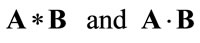
are denoted, respectively, the usual row column product and the element by element product.
Definition 2.1 Given two matrices 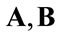 that have row order equal to m and column order equal to n, the following operation is defined:
that have row order equal to m and column order equal to n, the following operation is defined:
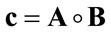
where c is the m elements vector in which the i-th component is obtained in the following way:
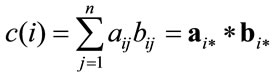
3. Homogeneous DTMRWP
Markov reward processes are a class of stochastic processes each of them with different evolution equations. The differences from the analytic point of view can be considered irrelevant but from the algorithmic point of view they are very significant and must be taken into account in the construction of the algorithms.
Let consider a discrete time homogeneous Markov chain with state space 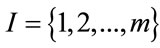 and transition probability matrix
and transition probability matrix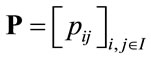 . As it is well known the n-step transition probability matrix is given by
. As it is well known the n-step transition probability matrix is given by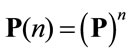 .
.
Definition 1: Let denote by 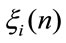 the discounted rewards accumulated in n periods given that at time 0 the system was in the state i and the reward are paid in the immediate case. It is defined recursively as follows:
the discounted rewards accumulated in n periods given that at time 0 the system was in the state i and the reward are paid in the immediate case. It is defined recursively as follows:
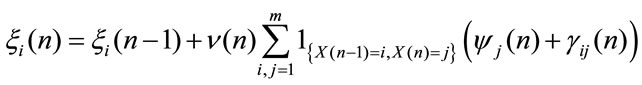 (1)
(1)
where 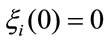
Similar relations can be easily written for discounted homogeneous due cases. We denote by:
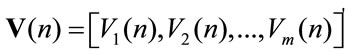
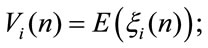
With 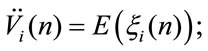 the mean present value of the rewards paid in the investigated horizon time in the due cases is represented. In this case, in the definition of the
the mean present value of the rewards paid in the investigated horizon time in the due cases is represented. In this case, in the definition of the 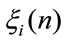 process we put
process we put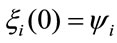 .
.
For the sake of understanding, first we present the simplest case in immediate and due hypotheses after only the general relations in the discrete time environment will be given.
The immediate homogeneous Markov formula in the case of fixed permanence and without transition rewards is the first relation presented. The DTMRWP present value after one payment is:
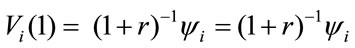
after two payments,
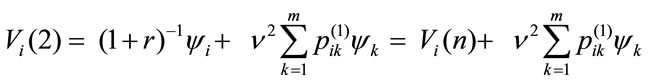
and in general, taking into account the recursive nature of relations, at n-th period it is:
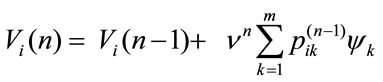
that in matrix form becomes:
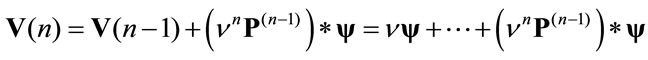
The general case with variable permanence, transition rewards and interest rates is presented. The present value after one period is:
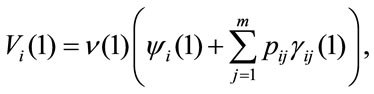
after two payments,
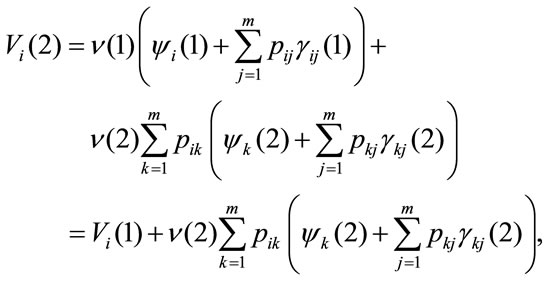
and in general, taking into account the recursive nature of relation, at n-th period it is:
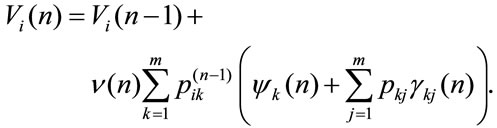 (2)
(2)
This relation can be written in matrix notation in the following way:
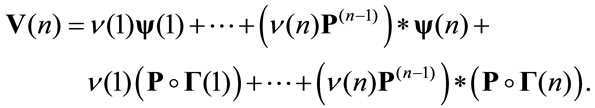
In the case of payment due the permanence reward is paid at beginning of the period and the transition reward at the end. It results:
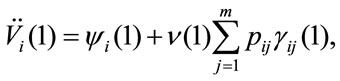
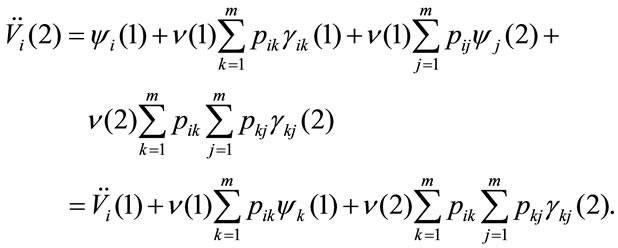
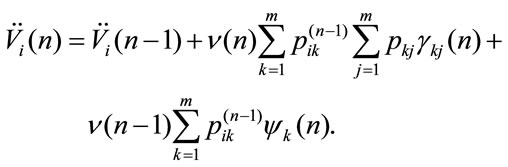 (3)
(3)
That in matrix notation is:
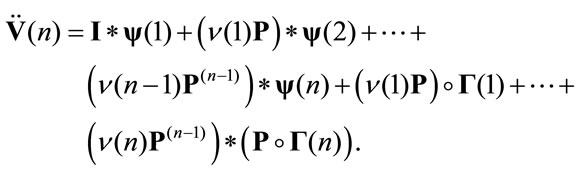
Remark 3.1 In this section, general formulas were presented. In the construction of the algorithms the differences between the possible cases should be taken into account. For example in the non-discounting case the following can be stated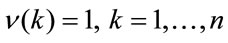 .
.
4. The higher Order Moments of Markov Reward Processes
In [11] relations for higher order moments of the integral of a generic function that evolves following a semiMarkov process were given. In more recent works (see [4] and [12]), the relations for higher moments of rewards associated to a semi-Markov backward system were presented.
In this section, following the methodology used in the last two quoted papers, the recursive relations useful for computing the higher moments in a Markov reward environment are provided.
It should be stated that the equations of this paper are different from that of [4] and [12] because we consider the conditioning on the starting state but also on the arriving state.
We will give only the discounted case.
According to Section 3 let us define the following stochastic process:
Definition 2: Let denote by 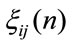 the accumulated discounted rewards in n periods given that at time 0 the system was in the state i and at time
the accumulated discounted rewards in n periods given that at time 0 the system was in the state i and at time 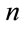 it will be in state j:
it will be in state j:
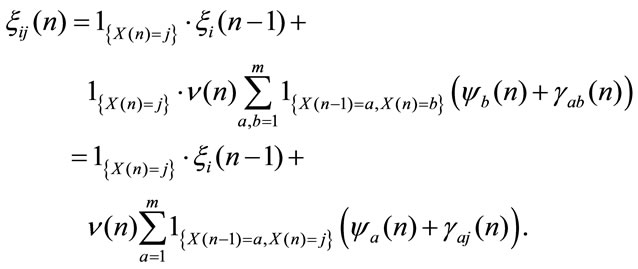 (4)
(4)
Moreover we denote
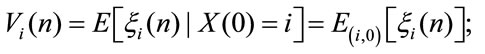
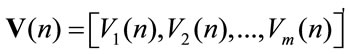
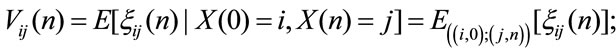
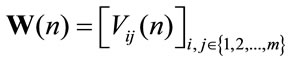
and the higher order moments are defined as
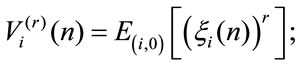
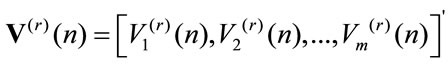
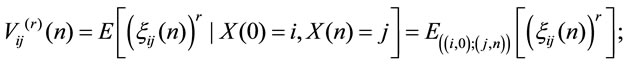
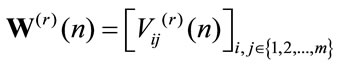
and it results for all r that 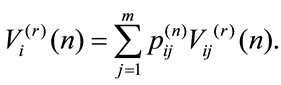
Similar relations can be easily written for non discounted cases Theorem 4.1 The moments of 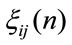 in the discounted immediate case, in matrix form, are given by:
in the discounted immediate case, in matrix form, are given by:
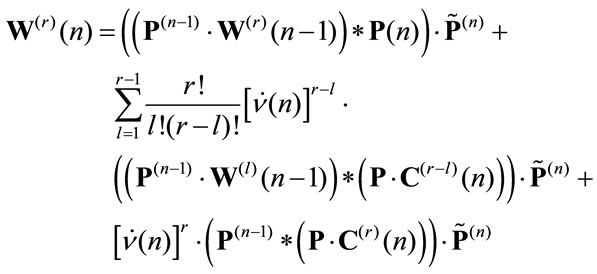 (5)
(5)
where:
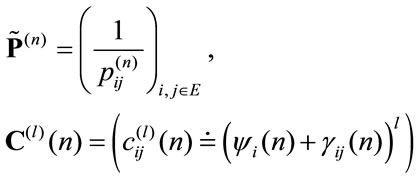
Proof From (4.1) it results:
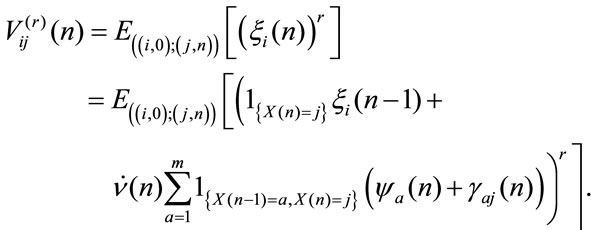
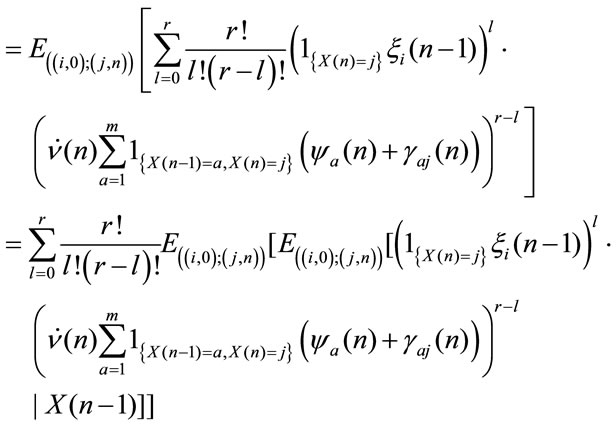
The random variables 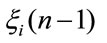 and
and 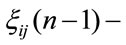
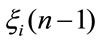 are independent given
are independent given 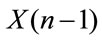 then we get in:
then we get in:
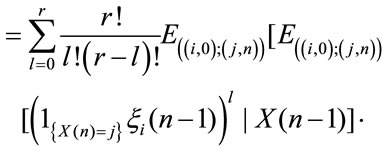
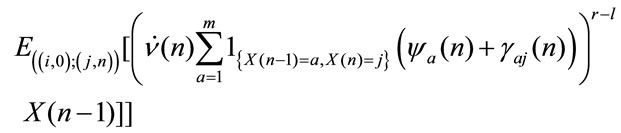
by independence between 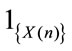 and
and 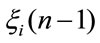 given
given 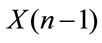 and by measurability of
and by measurability of 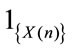 with respect to the information set
with respect to the information set 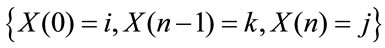 it results:
it results:
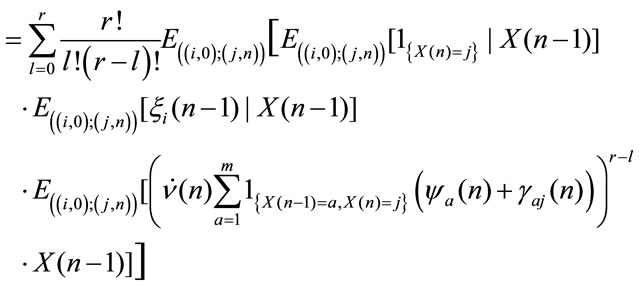
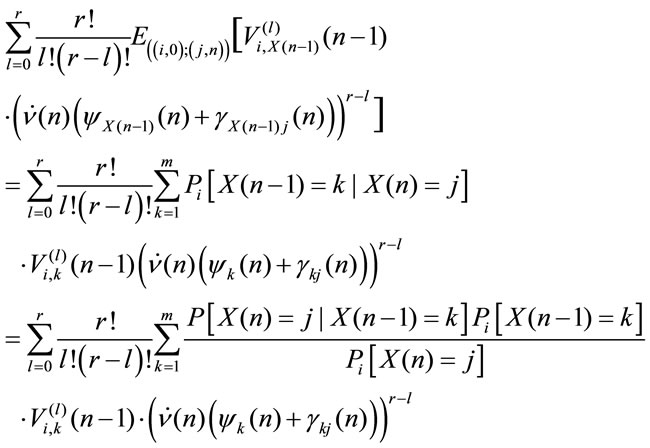
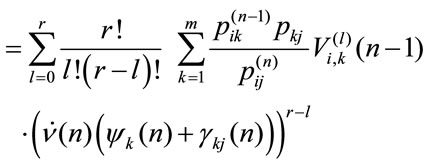
Consequently we obtain:
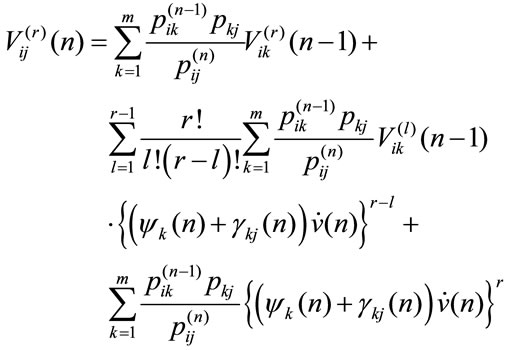
that in matrix form gives (5)
Now since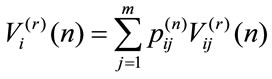 , by direct computation we get
, by direct computation we get 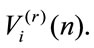
Corollary 4.1 The evolution equation of the higher order moment of the 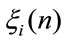 process in the discounted immediate case, in matrix form is:
process in the discounted immediate case, in matrix form is:
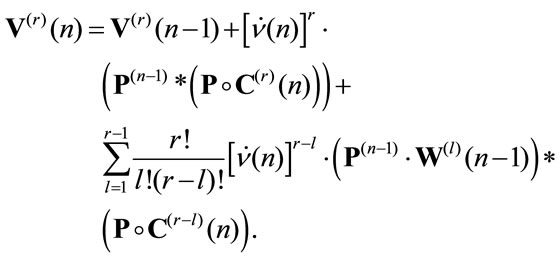 (6)
(6)
By means of similar procedures, the following corollaries can be obtained.
Corollary 4.2 The higher moments of 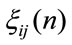 in the discounted due case, in matrix form, are given by the following relation:
in the discounted due case, in matrix form, are given by the following relation:
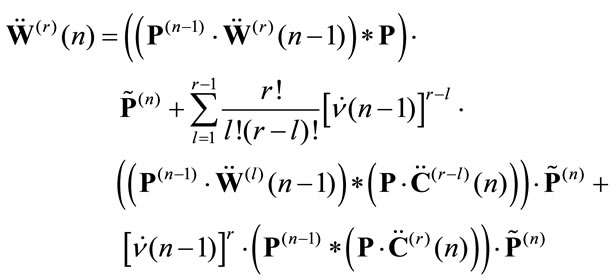 (7)
(7)
where: 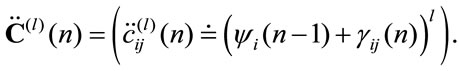
Remark 4.2 The possibility of computing the second order moments permits the obtaining of the variance and the sigma square, having in this way the opportunity to have a risk measure.
5. Motorcar Insurance Application
As it is well known, the bonus-malus motor car insurance model can be studied by means of Markov chains, see [13] for a complete description of bonus-malus systems. As far as the authors know, the premiums received and the benefits paid by the insurance company have never been studied simultaneously inside the evolution equation of the model as we propose here. In this way it is possible to have information on the future evolution of cash flows of the insurer and the possibility of computing higher order moments permits the obtaining of risk measures.
In order to apply DTMRWP we will construct a bonus-malus Markov reward model.
It should be noted that, as explained in [14], motor car insurance premiums could be a function of many factors such as type of car, mileage, age of the driver, region, sex and so on.
In Italy the only official distinctions are the province in which the car is insured and the power of its engine.
This example will use a transition matrix related to the motor car bonus-malus insurance rules that apply in Italy. In this case, the Markov model fits quite well because:
1) the position of each insured person is given at the beginning of each year2) there are precise rules that give the change of states in function of the behaviour of the policyholder person during the year3) the future state depends only on the present one.
The Italian bonus-malus rules are expressed by the function 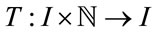 that to each rating class
that to each rating class  and number of accidents
and number of accidents 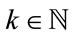 associates a new rating class
associates a new rating class 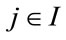 by means of the following law:
by means of the following law:
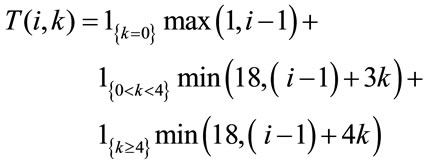 (8)
(8)
The range of values of T is 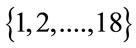 expressing the classes of risk in which all drivers are classified. The stochastic process
expressing the classes of risk in which all drivers are classified. The stochastic process 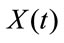 describing the rating risk class evolution of the policyholder is assumed to be a Markov chain with state space
describing the rating risk class evolution of the policyholder is assumed to be a Markov chain with state space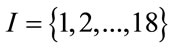 . This choice is determined by the fact that the next risk class is determined through rule (5.1) as a function of the current risk class
. This choice is determined by the fact that the next risk class is determined through rule (5.1) as a function of the current risk class 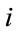 and the number of accidents
and the number of accidents 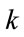 the policyholder carried out in the current year.
the policyholder carried out in the current year.
The authors are in possession of the history of 105627 insured persons over a period of three years. This means that it was possible consider 316881 real or virtual transitions. The data are related to the years 1998, 1999 and 2000. The estimated Markov transition matrix obtained from the available data taking into account the bonus-malus Italian rules is given in the Table 1. In this table we report only the transition probability that are possible to be observed, the remaining are impossible due to the Italian BMS rules. Then for example, in one step, from state 1 it is possible to migrate only towards state 1 (0 accident), to state 3 (1 accident), to state 6 (2 accident), to state 9 (3 accident) and to state 12 (4 or more accident). The other transitions are not allowable and then their probabilities are zero and then not reported in the table.
The payment of a claim by the insurance company can be seen as a lump sum (impulse or transition reward) paid by the insurer to the insured person.
In Figure 1 the premiums (they can be seen as permanence rewards) that are paid in Naples for a car of 2300 c.c. and in Oristano (a small Sardinian province) for a small car (about 1000 c.c.) are reported.
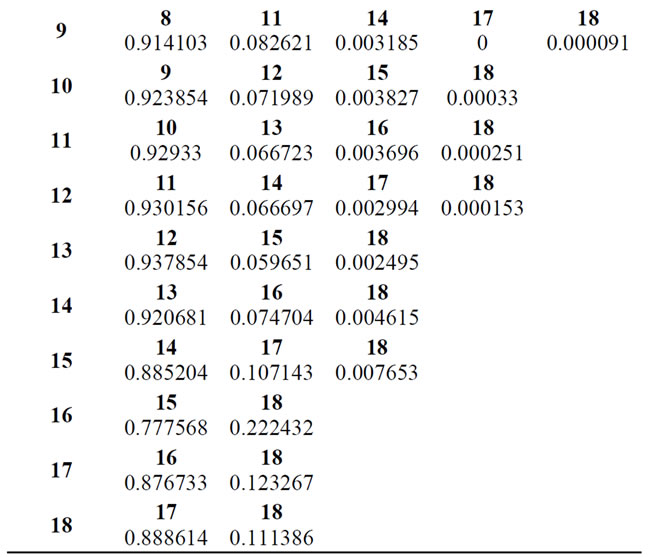
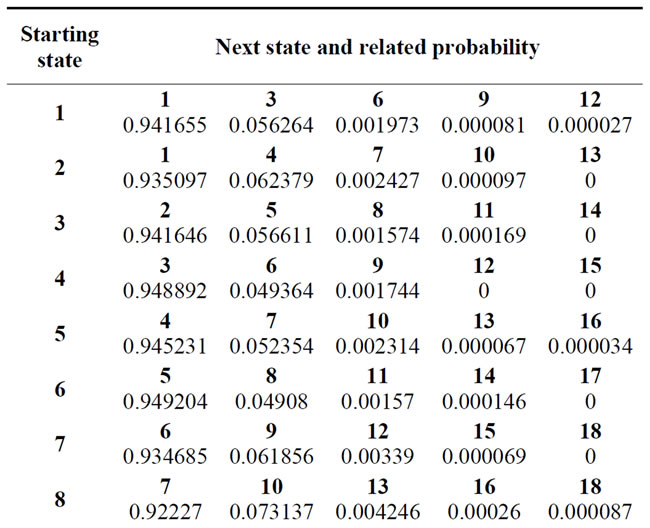
Table 1. One step transition probability matrix.
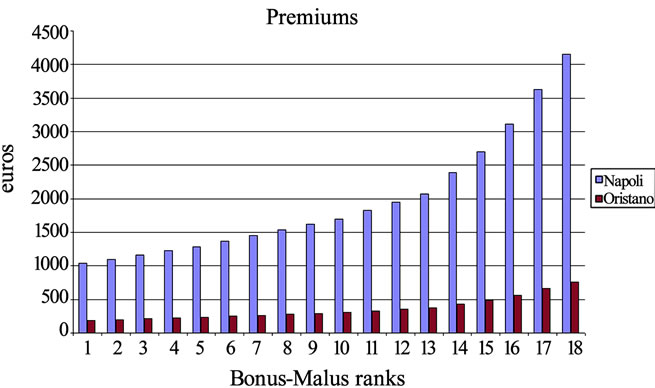
Figure 1. Naples and Oristano premiums.
The example is constructed from the point of view of the insurance company and premiums are an entrance for the company. It is to precise that these values correspond to the real premiums (that is loaded premiums covering costs and risk) paid by an insured in the year 2001 and officially given in the internet site of Assicurazioni Generali for that year.
In the example we suppose that the rewards are fixed in the time. Furthermore we suppose to have a yearly fixed discount factor of 1/1.03.
Table 2 gives the mean values of the expenses that the insurance company should pay for the claims made by the insured person.
More clearly stated, the element –7772.51 represents the expenses that, on average, the company has to pay for the two accidents that an insured person that was in the state 1 (lowest bonus-malus class) had and which then took him to state 6.
This table was constructed starting from the observed data in the authors’ possession.
From the point of view of the model, the elements of this table are transition rewards. More precisely, as already mentioned, they can be seen as lump sums (impulse rewards) paid by the company at the time of the accident. In this case, being expenses for the company, they result negative.
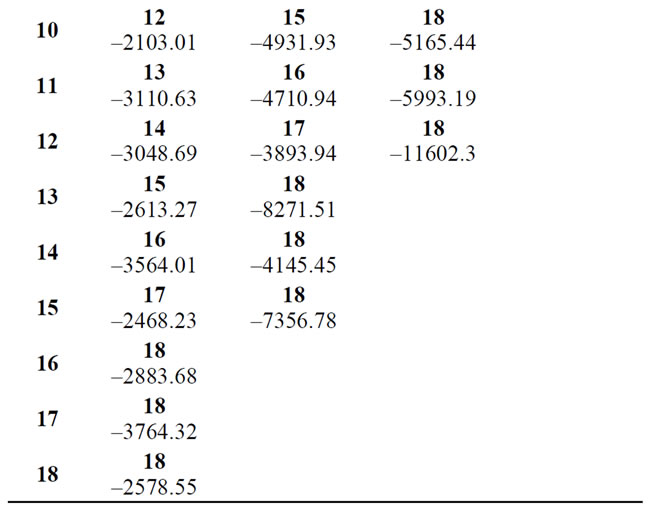
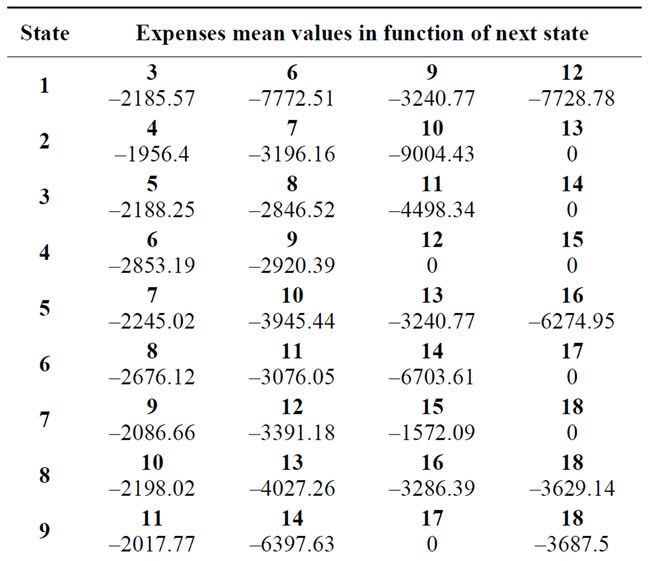
Table 2. Mean insurance payments.
In Figure 2 are resumed in the first part the reward mean present values and in the second the related sigma square.
The permanence reward (insurance premium) increases in function of the state and, therefore, the money earned by the company increases in function of the starting state too. It is to observe that the Insurance company always earns. Only in one case in Oristano (the first year of the 16th rank) it looses some small sum.
The illustrated case is very particular. In Naples the premiums are higher than in the other part of Italy, the car is big and also for this reason the premiums are very high. In Oristano the premiums are among the lowest in Italy and we consider a small car.
6. Conclusions
The description of homogeneous Markov reward processes was presented. For the first time, at author knowledge, the relations useful to compute the higher moments for homogeneous Markov reward processes conditioned on the starting and arriving states are given. By means of the higher order moments it is possible to obtain variability indices.
The model was applied to motor car insurance regulations in Italy. The mean present values of rewards were computed. The results related to Naples and Oristano provinces were shown.
The authors hope to get a wider data set to construct a more reliable example and to understand if these first results that were obtained by the available data could be confirmed.
7. Acknowledgements
The authors are grateful to colleagues and friends Patrizia Gigante, Liviana Piceh and Luciano Sigalotti that
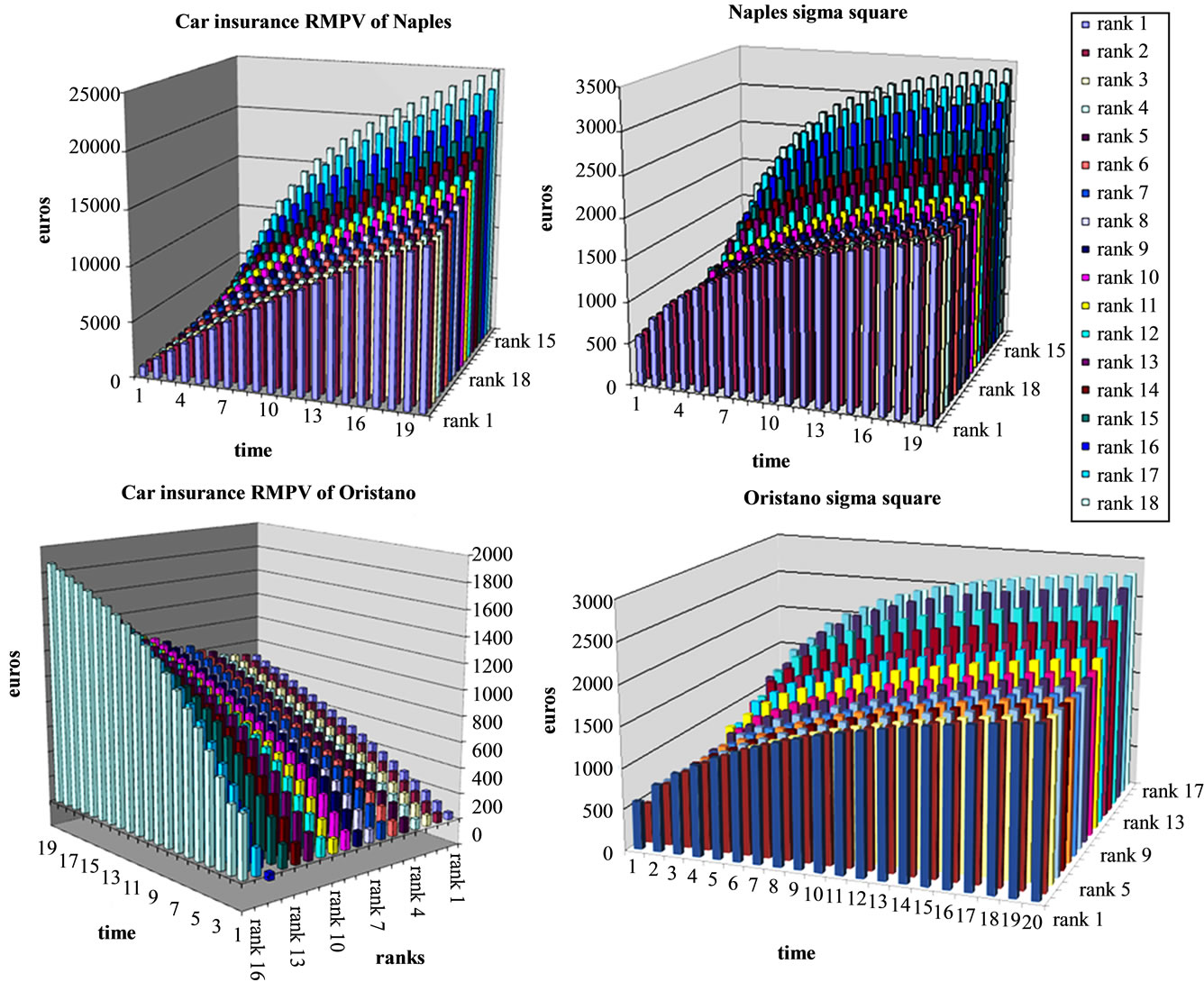
Figure 2. Mean present values and variances of Naples and Oristano rewards.
gave the data for the applications. The work was supported by a PRIN-MIUR and a Università di Roma “La Sapienza” grants.
8. References
[1] Howard R, “Dynamic Probabilistic Systems,” vol. 1-2, Wiley, New York, 1971.
[2] R. Norberg, “Differential Equations for Moments of Present Values in Life Insurance,” Insurance: Mathematics and Economics, Vol. 17, No. 2, 1995, pp.171-180.
[3] J. Janssen and R. Manca, “Applied Semi-Markov Processes,” Springer, New York, 2006.
[4] F. Stenberg, R. Manca and D. Silvestrov, “An Algorithmic Approach to Discrete Time Non-Homogeneous Backward Semi-Markov Reward Processes with an Application to Disability Insurance,” Methodology and Computing in Applied Probability, Vol. 9, No. 4, 2007, pp. 497-519.
[5] J. Janssen and R. Manca, “Semi-Markov Risk Models for Finance, Insurance and Reliability,” Springer, New York. 2007.
[6] J. Janssen, R. Manca and di P. E. Volpe, “Mathematical Finance: Deterministic and Stochastic Models,” STE and Wiley, London, 2008.
[7] S. G. Kellison, “The Theory of Interest,” 2nd Edition, Homewood, Irwin, 1991.
[8] M. A. Qureshi and H. W. Sanders, “Reward Model Solution Methods with Impulse and Rate Rewards: An Algorithmic and Numerical Results,” Performance Evaluation, Vol. 20, No. 4, 1994, pp. 413-436.
[9] J. M. Hoem, “The Versatility of the Markov Chain as a Tool in the Mathematics of Life Insurance,” Transactions of the 23rd International Congress of Actuaries, vol. 3, 1988, pp. 171-202.
[10] H. Wolthuis, “Life Insurance Mathematics (the Markovian Model),” 2nd Edition, Peeters Publishers, Herent. 14, 2003.
[11] E. Çinlar, “Markov Renewal Theory,” Advances in Applied Probability, Vol. 1, 1969, pp. 123-187.
[12] F. Stenberg, R. Manca and D. Silvestrov, “Semi-Markov Reward Models for Disability Insurance,” Theory of Stochastic Processes, Vol. 12, No. 28, 2006, pp. 239-254.
[13] J. Lemaire, “Bonus-Malus Systems in Automobile Insurance,” Kluwer Academic Publisher, Boston, 1995.
[14] B. Sundt, “An Introduction to Non Life Insurance Mathematics,” Veroffentlichungen des Istitute fur Versich-erun gswissenschaft der Universitat Mannheim, 3rd Edition, 1993.
NOTES
*Work supported by a MURST grant.

