Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 4 (2010) , Article ID: 1683 , 6 pages DOI:10.4236/jemaa.2010.24035
Investigation of Electric Fields Inside & Outside a Magnetized Cold Plasma Sphere
![]()
1Institute of Radio Wave Propagation & Scattering, Xianyang Normal University, Xian Yang, China; 2School of Science, Xidian University, Xian, China.
Email: liyinglexidian@yahoo.com.cn
Received January 8th, 2010; revised February 17th, 2010; accepted February 20th, 2010.
Keywords: Magnetized Cold Plasma, Scales Transformation, Electric Field
ABSTRACT
The analytical expressions of electric fields inside and outside a magnetized cold plasma sphere are presented by reforming the spherical electromagnetic parameter based on the scales transformation of electromagnetic theory. The obtained results are in good agreement with that in literatures. The angle between the direction of inside field and that of outside field is derived. In S wave band, numerical calculations of effects induced on the inner field by parameters are established. Simulations show that the angle between incident field and the outside magnetic field influences the inner field remarkably. The inner field will decrease as the electron density increasing, however, this density has a great affect on the inner field’s direction. The magnitude of the inner field is proportional to the incident wave’s frequency.
1. Introduction
The investigations both for electromagnetic (EM) scattering features and their applications of spherical target have been of a great interest. The electric fields inside and outside a single isotropic dielectric sphere have been researched [1-4]. The scattering features of an isotropic dielectric sphere and a conducting sphere, which are irradiated by an EM wave propagating in the z-direction and polarizing in the x-direction, have been studied [5,6]. By using method of rotating coordinate system, the scattering properties of spherical targets that are irradiated by a wave from an arbitrary direction is studied [6]. In [7-10], the EM scattering features for an isotropic dielectric ellipsoidal target and the power to seize radiation for a coated sphere in the Gaussian beam were separately investigated by the well-known Mie theory. In a word, the subjects of electromagnetic scattering and their applications of an isotropic dielectric sphere have been discussed in detail. However the scattering features for the magnetized cold plasma have not been fully understood in theory. There may be two main reasons for this, the first is the lack of analytical expression of electric field inside the magnetized cold plasma being irradiated by a wave from an arbitrary direction, the second is that some wave equations and functions derived in the isotropic space are now invalid in the anisotropic space.
Many particles are practically anisotropic and much smaller than the wave length in size, such as raindrops, sand-dust storm particulates, fog droplets, etc. Therefore the problems relative to electromagnetic field may be approximately considered as an electrostatic one [3]. If the inside electric field is known, the absorption cross section and the scattering cross section of the anisotropic sphere will be obtained accurately [11], so knowing the inside field existing the target is of great importance. In the present paper, the expression of the electric field inside a magnetized cold plasma spherical target is presented first based on the scale transformation theory of the electromagnetic field by reforming the anisotropic electromagnetic parameters into an isotropic one. Then the angle between the field inside the magnetized plasma sphere and that outside the sphere is calculated. Finally the influences induced by the fundamental parameters such as electric density, outside magnetic filed and the azimuth angle on the inner field are simulated. The method used has the features of briefness in computation and distinctness in physical significance.
2. Electric Fields inside and outside a Magnetized Cold Plasma Sphere
2.1 Foundation of Potential Differential Equation
Assume a magnetized cold plasma sphere to have radius R0 and its centre to be located at the origin of the primary coordinate system Σ. The outside magnetic field 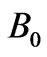 is in z-axis. The dielectric constant tensor of this plasma is given as
is in z-axis. The dielectric constant tensor of this plasma is given as
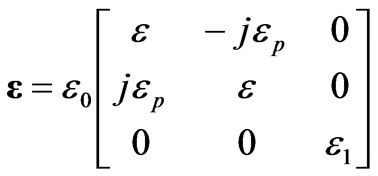 (1)
(1)
where
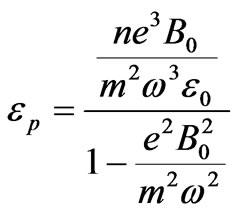 ,
, 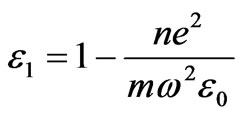 ,
, 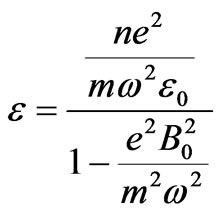
n is electron density and 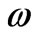 the frequency of incident wave. When the frequency is low, Raleigh criterion
the frequency of incident wave. When the frequency is low, Raleigh criterion 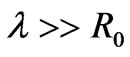 is valid, it is so approximately think that the magnetized cold plasma sphere locates in the electrostatic field [1,3]. The plasma has not electric charge in whole. According to
is valid, it is so approximately think that the magnetized cold plasma sphere locates in the electrostatic field [1,3]. The plasma has not electric charge in whole. According to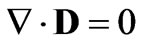 ,
, 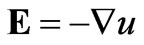 and considering that the differential of potential u is not relative to the differential order for x and y, the potential differential equation is obtained in the primary coordinate system as
and considering that the differential of potential u is not relative to the differential order for x and y, the potential differential equation is obtained in the primary coordinate system as
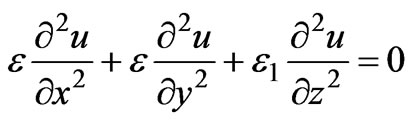 (2)
(2)
Now, a scale coordinate system Σ’ is introduced as a new coordinate system. The coordinates of this system are indicated with x′, y′ and z′. The relation of coordinates between the two systems is written as
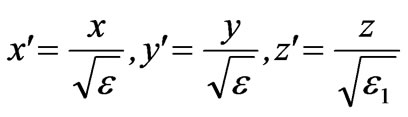
The differential equation of the potential in the scale coordinate system is derived by substituting the above expressions into Equation (2) and using the condition u = u′ [12,13] at any spatial point, Equation (2) may be expressed as
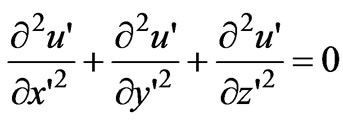 (3)
(3)
The condition u = u′ is understandable, for the potential is defined as the work done by the electric field to move a unit charge from one point to the reference point, namely W/q, so both the numerator and the denominator are scale invariants. Equation (3) shows that a magnetized cold plasma sphere in the primary coordinate system is transformed into an isotropic sphere in the scale coordinate system. This manipulation may greatly simplify the electromagnetic scattering problems.
2.2 Expressions of Electric Fields outside and inside a Magnetized Cold Plasma Sphere
The solution of Equation (3) can be obtained by using the method of separation of variables as follows:
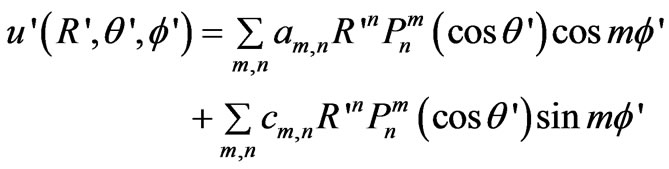 (4)
(4)
Equation (4) is a general solution in the scale coordinate system. The parameters in the two coordinate systems are related, their relationships [12,13] are
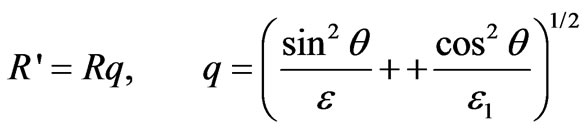
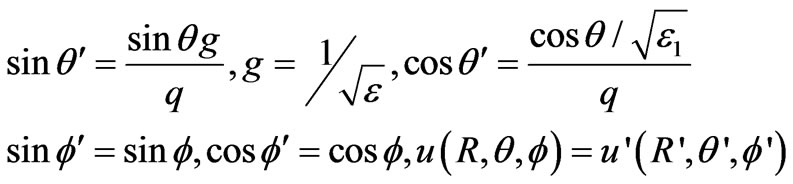
In Equation (4), the term that may produce a finite potential in the sphere centre is considered. It is concluded that the expression of potential in the primary coordinate system can be obtained only by substituting the relations above into Equation (4). By utilizing the relation between D and E and the relation between the vectors in right angle system and spherical system, we may also obtain the expression of the dielectric constant tensor in spherical coordinate system as
 (5)
(5)
where
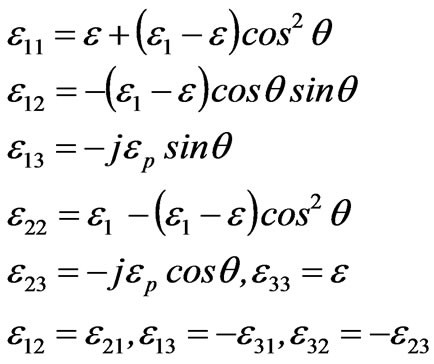
We suppose that E0 is the magnitude of incident electric field, and that θ0 and φ0 are its directional parameters in the primary coordinate system. As shown in Figure 1, since the outside electric potential is not symmetrical, we can write the potential as [2]
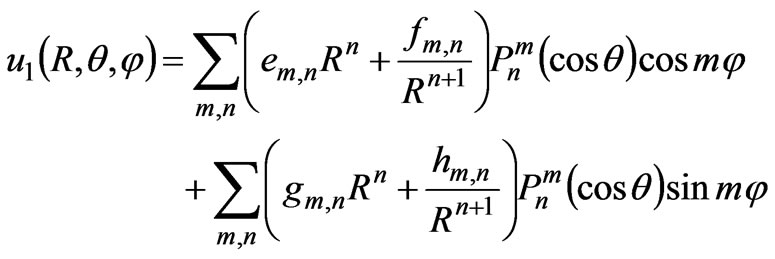 (6)
(6)
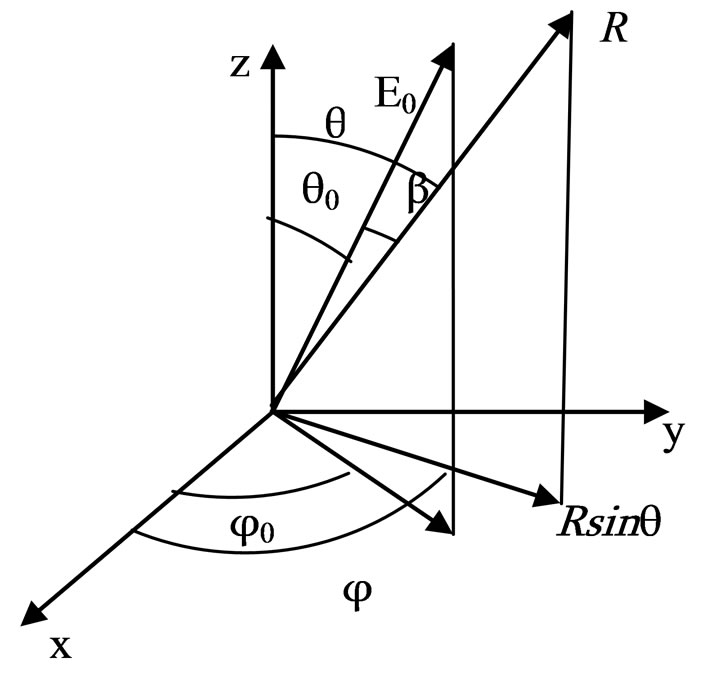
Figure 1. Relation between the observing point and the outside electric field E0
When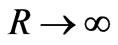 ,the electric potential near to
,the electric potential near to
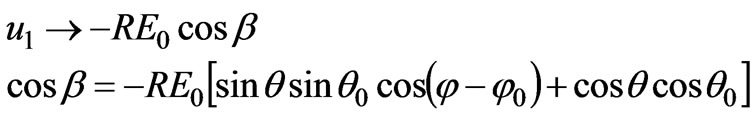
Comparing the coefficients of the above expression with those in Equation (6) yields
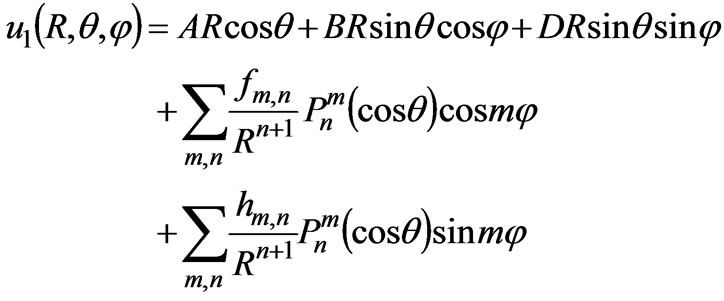
where 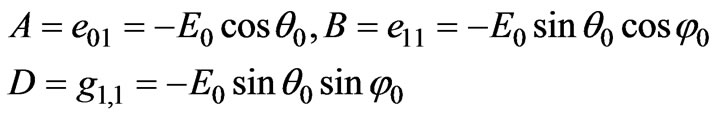
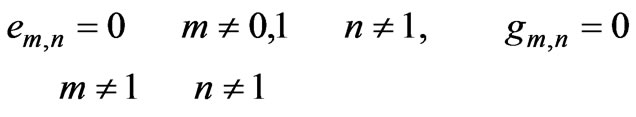
Equations (4) and (6) are the electric potentials inside and outside the magnetized cold plasma sphere respectively. On the surface of the sphere, the electric potential inside the sphere is equal to that outside the sphere and the electric displacement D0 is continuous in the normal direction, namely
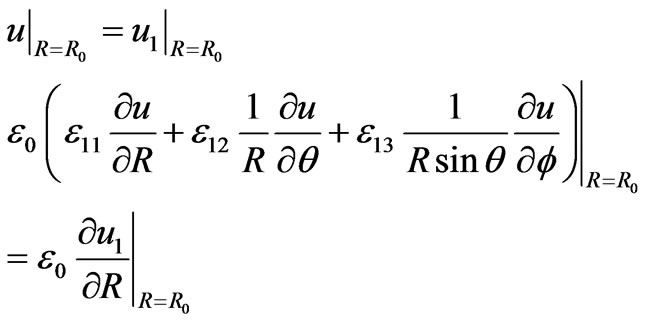 (7)
(7)
Inserting Equations (4)-(6) into the above conditions yields
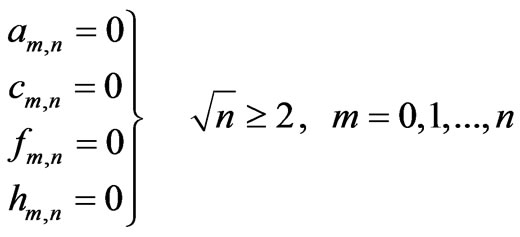
There are three types of trigonometric functions in the above expressions, namely
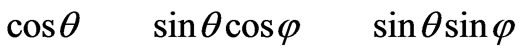
Comparing their coefficients, we may obtain the following matrix equation
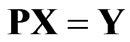 (8)
(8)
where

The solution of Equation (8) is easy derived as
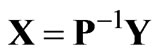 (9)
(9)
Namely

We thus obtain the solution of electric potential inside and outside a magnetized cold plasma sphere as
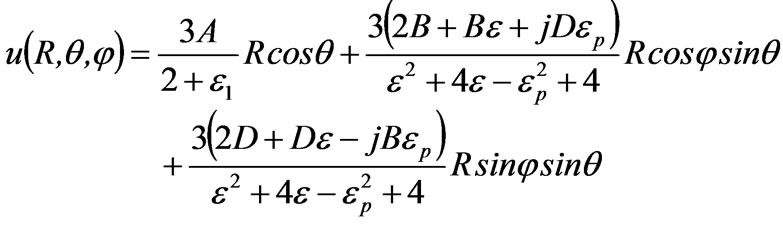 (10)
(10)
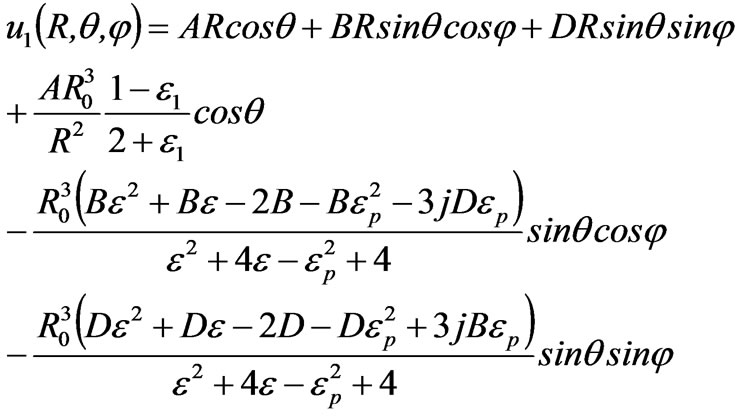 (11)
(11)
2.3 Discussions
From Equation (6) it follows that when θ0 = φ0 = 0, the incident electric field E0 is in the z-direction, B = D = 0,and A = –E0. If we suppose that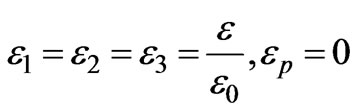 ,now the problem of the electric field in a magnetized cold plasma medium has been changed into a question in the isotropic medium. Equations (10) and (11) are transformed, respectively, into the following expressions:
,now the problem of the electric field in a magnetized cold plasma medium has been changed into a question in the isotropic medium. Equations (10) and (11) are transformed, respectively, into the following expressions:
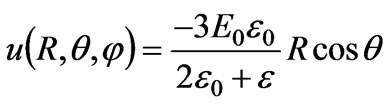
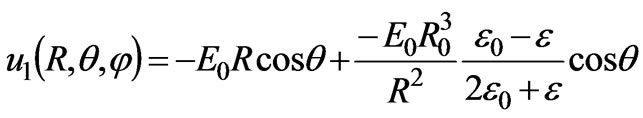
From [3,4,14], we obtain the solutions of an isotropic dielectric sphere in electric field E0. These solutions may be given as
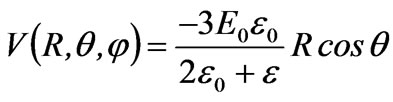
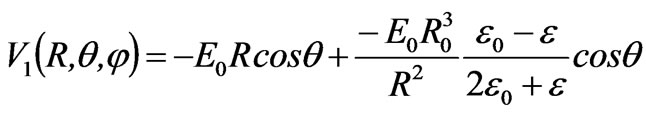
It can be seen that the results are consistent entirely with those in the literature. The correctness of the obtained results is therefore tested. Let 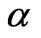 and
and 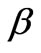 be the angles between E0 and the x-axis and between E0 and the y-axis, respectively, then it will be easily proved that
be the angles between E0 and the x-axis and between E0 and the y-axis, respectively, then it will be easily proved that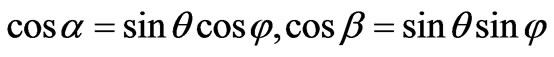 . So the second term and the third term in Equation (10) are the potential produced by the polarizing electrical dipole moment respectively in x-direction and in y-direction. In the scattering of small particles, for example, Raleigh scattering, the electric field inside the target is of great importance. So we must discuss the distribution of the inside electric field in detail. The electric field is obtained by making a gradient from Equation (10) and utilizing the transformation between a vector respectively in the spherical coordinate system and the right angle coordinate system as follows:
. So the second term and the third term in Equation (10) are the potential produced by the polarizing electrical dipole moment respectively in x-direction and in y-direction. In the scattering of small particles, for example, Raleigh scattering, the electric field inside the target is of great importance. So we must discuss the distribution of the inside electric field in detail. The electric field is obtained by making a gradient from Equation (10) and utilizing the transformation between a vector respectively in the spherical coordinate system and the right angle coordinate system as follows:
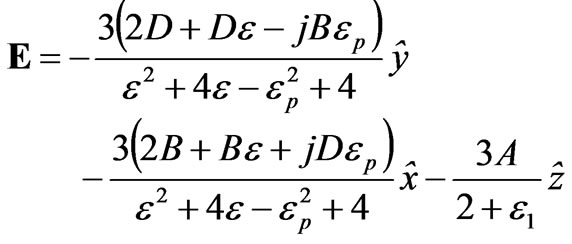 (12)
(12)
Equation (12) demonstrates that the electric field inside a magnetized cold plasma sphere is a uniform field which is a complex function of the incident azimuth angle, outside magnetic field, the electric density and the frequency etc. This field makes an angle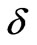 with respect to the incident field E0. This cosine function for this angle is easily derived by taking the scalar product of vectors as follows:
with respect to the incident field E0. This cosine function for this angle is easily derived by taking the scalar product of vectors as follows:
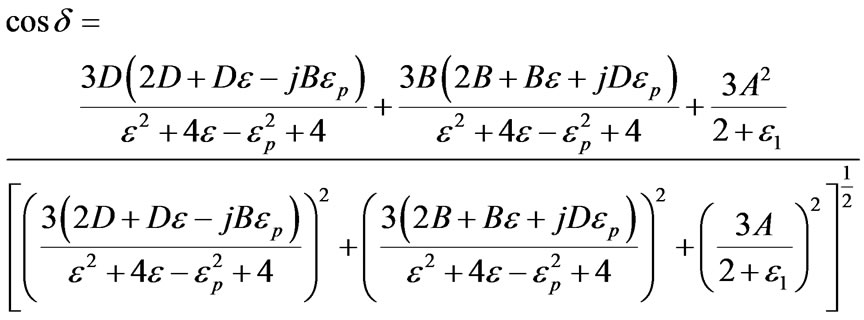 (13)
(13)
where 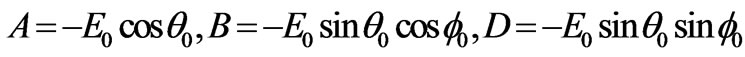
It is a function of the azimuth angle. The displacement D is easy obtained from Equations (1) and (12), it is not presented here in detail. Followings are partial numerical results:
According to the literature [15], the parameters used in simulations are f = 3 GHz,n = 4.5 × 1017 m-3. It is con-
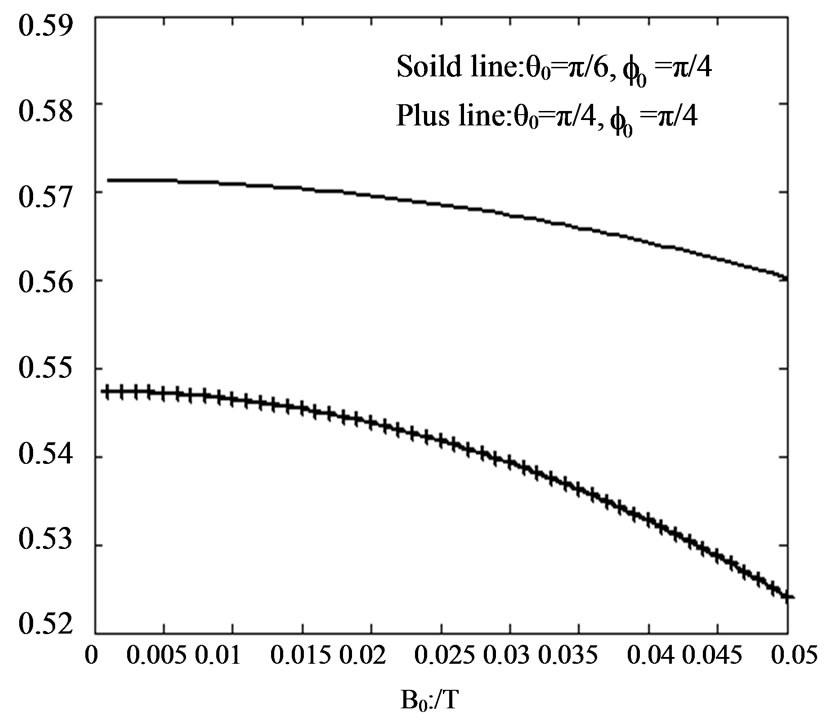
Figure 2. Electric field changes with outside magnetic field
cluded from Figure 2 that the inner field will decrease when the outside magnetic field increase. The angle 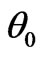 between the outside electric field and the outside magnetic field has a great effect on the field inside the plasma and further simulations show that angle
between the outside electric field and the outside magnetic field has a great effect on the field inside the plasma and further simulations show that angle 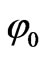 has not affect on the inner field. This is because that the anisotropic property in plasma is caused by the outside magnetized field, the components of outside electric field are relative to the angle
has not affect on the inner field. This is because that the anisotropic property in plasma is caused by the outside magnetized field, the components of outside electric field are relative to the angle 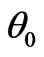 and angle
and angle 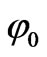 has a good symmetry to outside magnetic field, so the inner field does not varying with angle
has a good symmetry to outside magnetic field, so the inner field does not varying with angle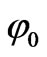 . In Figure 3, the azimuth angles are
. In Figure 3, the azimuth angles are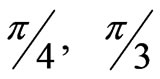 . It is demonstrated that the inner electric field decrease as the electron density increasing. This is caused by the reason that when the electron density increases, the electrical conductivity is also strong, so the shield of electric field is enhanced. It is also can be seen from Figure 4 that the inner field is proportional to the operating frequency. This is due to the reason that the variety of electric charges inside plasma not agreement with that of outside electric field and the shielding effect is thus debased. Figure 5 had conducted the change of angle
. It is demonstrated that the inner electric field decrease as the electron density increasing. This is caused by the reason that when the electron density increases, the electrical conductivity is also strong, so the shield of electric field is enhanced. It is also can be seen from Figure 4 that the inner field is proportional to the operating frequency. This is due to the reason that the variety of electric charges inside plasma not agreement with that of outside electric field and the shielding effect is thus debased. Figure 5 had conducted the change of angle 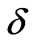 versus the frequency. The solid line and dotted line are nearly superposed in which the density n = 4.5 × 1017 m-3 and outside magnetic fields B0 are respectively 0.004T and 0.005T. Another density of n = 8 × 1017 m-3 is used in the second dotted line. It obviously demonstrates that the outside magnetic field has not a great influence on the angle and however the electron density has a great effect on it. The angle is proportional to the frequency. It is well known that in isotropic medium, the angle
versus the frequency. The solid line and dotted line are nearly superposed in which the density n = 4.5 × 1017 m-3 and outside magnetic fields B0 are respectively 0.004T and 0.005T. Another density of n = 8 × 1017 m-3 is used in the second dotted line. It obviously demonstrates that the outside magnetic field has not a great influence on the angle and however the electron density has a great effect on it. The angle is proportional to the frequency. It is well known that in isotropic medium, the angle 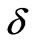 is zero, so in the time varying electromagnetic field, the electric charges, negative and positive, in the cold plasma can not agreement with outside field as the frequency being augment which causes the angle’s accretion.
is zero, so in the time varying electromagnetic field, the electric charges, negative and positive, in the cold plasma can not agreement with outside field as the frequency being augment which causes the angle’s accretion.
3. Conclusions
In this paper, the electric fields inside and outside a magnetized cold plasma sphere are investigated. We use the scale transformation theory of the electromagnetic field to reconstruct the Laplace equation and then obtain two analytical expressions of the electric potentials inside and outside the magnetized cold plasma sphere in detail. The obtained results are consistent with those in the literature when the dielectric constant tensor becomes that in an isotropic medium. The angle between the total fields inside and outside the magnetized cold plasma sphere is derived. The effects induced by the incident direction, outside magnetic field, frequency etc. on the direction and the magnitude of the inside electric field are simulated. Due to many particles such as sand-dust storm particulates, atomy particles and raindrops are generally anisotropic, so the results obtained can provide
Figure 3. Electric field changes with electron density
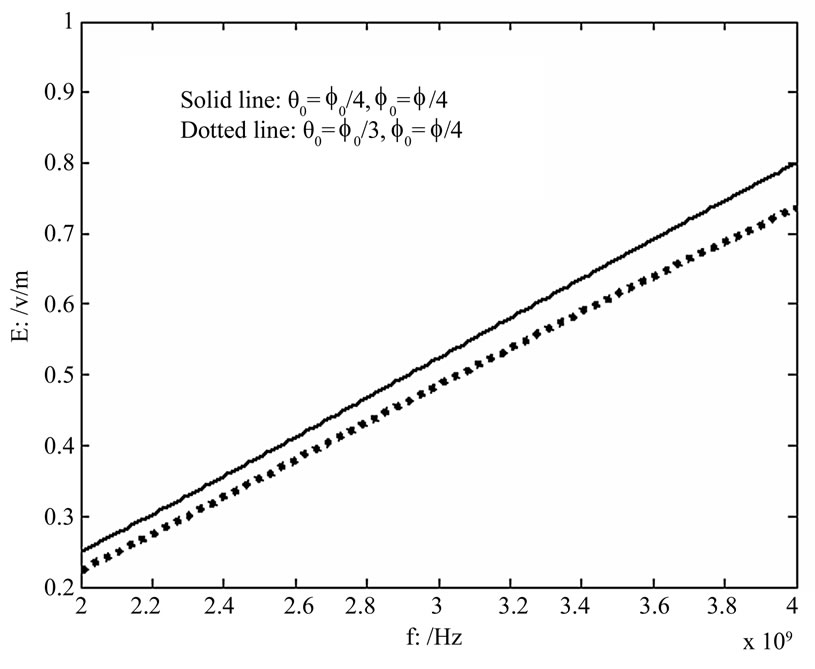
Figure 4. Electric field changes with frequency
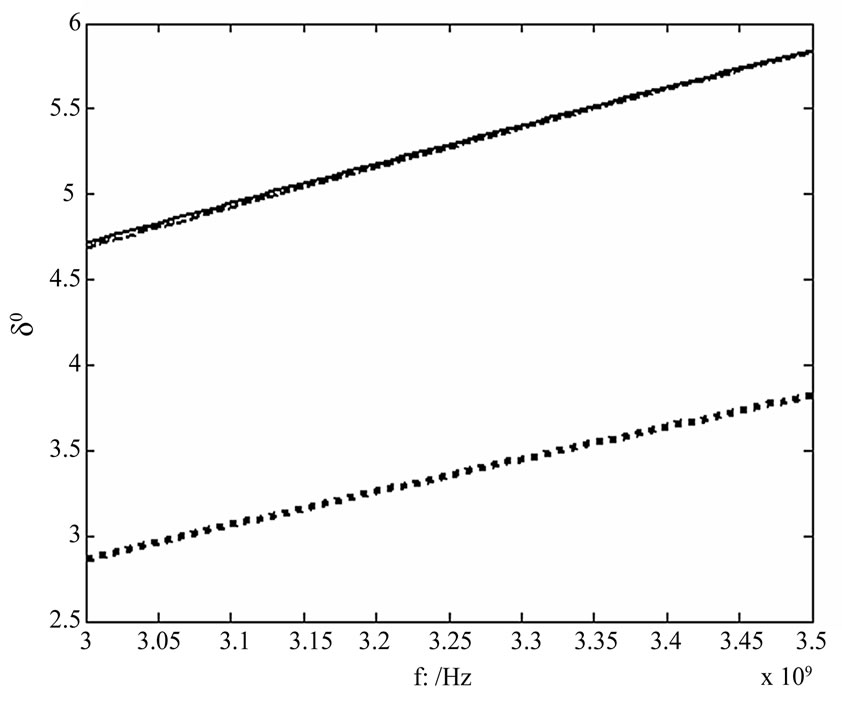
Figure 5. Angle δ changes with frequency
a good theoretical foundation for studying the scattering features of small particles and magnetized cold plasma. How to use the scale transformation theory to study the electromagnetic fields inside and outside a magnetized cold plasma target irradiated by the time-varying electromagnetic wave is our next research subject.
4. Acknowledgments
This project was supported by the National Natural Science Foundation of China (Grant No. 60971079, 60801047), the Natural Science Foundation of Shaanxi Province (Grant No. 2009JM8020) and Natural Science Foundation of Shaanxi Educational Office (Grant No. 09JK800).
REFERENCES
- D. K. Cheng “Field and Wave Electromagnetics,” Pearson Education Addison-Wesley, Massachusetts, 2006.
- J. A. Stratton “Electromagnetic Theory,” McGraw-Hill, New York, 1941.
- A. Ishimaru, “Wave Propagation and Scattering in Random Medium,” Part I, Academic Press, New York, 1978, pp. 27-30.
- A. K. Jin, “Electromagnetic Wave Theory,” Electronics Industry Press, Beijing, 2003, pp.305-312.
- Y. P. Wang and D. Z. Cheng, “Engineer Electrodynamics,” Press of Xidian University, Xian, 1985.
- Y. L. Li and J. Y. Huang, “The Scattering Fields for a Spherical Target Irradiated by a Plane Electromagnetic Wave in an Arbitrary Direction,” Chinese Physics, Vol. 15, No. 2, 2006, pp. 281-285.
- H. Huang, Y. Fan, B. Wu, F. Kong and J. A. Kong, “Surface Modes at the Interfaces Between Isotropic Media and Uniaxial Plasma,” Progress in Electromagnetics Research, Vol. 76, 2007, pp. 1-14.
- Y. P. Han, Y. G. Du and H. Y. Zhang, “Radiation Trapping Forces Acting on a Two-Layered Spherical Particle in a Gaussian Beam,” Acta Physica Sinica, Vol. 55, No. 9, 2006, pp. 4557-4560.
- L. Bai and Z. S. Wu, “Scattering of Fundamental Gaussian Beam from On-Axis Cluster Spheres,” Acta Physica Sinica, Vol. 54, No. 5, 2005, pp. 2025-2030.
- J. R. Bottiger, Y. L. Fan, B. Stout, J. C. Auger and S. Holler, “Observations and Calculations of Light Scattering from Clusters of Spheres,” Applied Optics, Vol. 39, No. 36, 2000, pp. 6873-6887.
- L. Tsang, J. A. Kong and K. H. Ding, “Scattering of Electromagnetic Waves,” John Wiley & Sons, New York, 2000, pp. 9-26.
- Y. L. Li and J. Y. Huang, “The Scale-Transformation of Electromagnetic Theory and its Applications,” Chinese Physics, Vol. 14, No. 4, 2005, pp. 646-656.
- Y. L. Li and J. Y. Huang, “Scales Transformation Theory of Electromagnetic Field and its Applications,” Press of Xidian University, Xian, 2006.
- L. Q. Xu and W. Cao, “Electromagnetic Field and Electromagnetic Theory,” Science Press, Beijing, 2006, pp. 88-90.
- S. B. Liu, J. J. Mo and N. C. Yuan, “Research on the Absorption of EM-Wave by Inhomogeneous Magnetized Plasmas,” Acta Electronica Sinica, Vol. 31, No. 3, 2003.

