Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 2 (2010) , Article ID: 1394 , 4 pages DOI:10.4236/jemaa.2010.22017
3D Diffractive Focusing THz of In-Plane Surface Plasmon Polarition Waves
![]()
Novosibirsk State Technical University, Russia.
Email: igor.minin@ngs.ru, prof.minin@gmail.com
Received September 11th, 2009; revised October 22nd, 2009; accepted October 28th, 2009.
Keywords: Diffractive Optical Element, Surface Plasmon Polarition Waves, Three Dimension
ABSTRACT
Demonstrated that analog of diffractive and refractive 3D optics in free space can be developed to manipulate surface waves such as surface plasmon polaritons (SPPs). It has been shown that an air-gap control of a floating dielectric block can generate the dynamic phase and amplitude modulation of the SPP transmission coefficient. Unlike conventional bulk optics, the nano-scale surface optics for SPP processing contains several unexpected and interesting features in addition to the physical features described. Dynamic plasmonic information processing on the nano-scale using air-gap control may be an effective mechanism for building a dynamic plasmonic information processing system.
1. Introduction
THz and optical information processing on the nano-scale is considered to be a main objective in the field of nanophotonics. Recently, THz and optical information processing on the nano-scale has become a reality because of the exploitation of the full potential of surface plasmon polaritons (SPPs) [1–3]. SPPs are electromagnetic surface waves formed through strong interaction between electromagnetic field and free electron oscillations at a metal-dielectric interface. It is strongly desired to excite and control propagating SPP fields in a systematic fashion as is possible with optical fields both in free space and dielectric waveguides. One of unique properties of the SPPs is that SPPs wavelength can be shorter than the wavelength of radiation in surrounding media, leading to applications in sub-diffraction-limited techniques.
Discovering this effect birthed many new research areas in SPP/subwavelength optics or other spectral band fields. To realize the promise of SPP technologies, a comprehensive arsenal of optical elements for launching, detecting, guiding, imaging, focusing, and otherwise transforming SPP waves must be readily available. Once the basic optical manipulation of SPP has become routine, it will pave the way for more sophisticated devices, including different wavebands, possibly including confocal microscopes with sub-diffraction limited resolution obtained by focusing of SPP fields [4].
Surface electromagnetic effects could enhance the efficiency of numerous physical and chemical processes [7], as these effects lead to an increase of the electromagnetic fields at the surface, giving rise to an improved experimental sensitivity. In particular, the excitation of surface plasmons (SP) [8] at the metal surface may increase by three orders of magnitude the intensity of optical beams generated at the surface, like Raman or second harmonic signals [9].
A SP corresponds to the quantum of energy associated to a harmonic oscillation of the free charges at the metal surface (the SP wave), which is mostly perpendicular to the surface and which propagates along the surface. Solving Maxwell equations (homogeneous problem) for this interface leads to the SP dispersion relation:
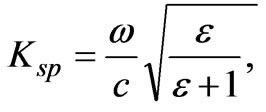
where ε is the dielectric constant of the metal, Ksp—wave number of SP, ω=2π/λ, λ is a wavelength in free space. So we solved the material problem, but to match the moments, we can choose one of three main techniques. The first technique uses a prism and total internal reflection; the second one involves scattering from a topological defect like small holes in a thin film. The third technique makes use of periodic corrugations in the metal’s surface.
In the far infrared, this dielectric constant takes large values, thus:
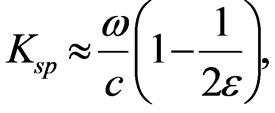
The energy coupled to the SP is diffracted by the grating while SP propagates along the grating surface.
2. Diffractive Focusing Element Design
Several parabolic lens structures for SPPs have been demonstrated [10,11]. Recently, a double slit experiment of SPPs [12] was reported to show that the lowdimensional diffraction theory analogue to Fresnel diffraction theory is applicable to SPPs.
We propose a novel SPP focusing approach using an in-plane SPP 3D conical Fresnel zone plate [5] (FZP) in which the designed rules are strictly following traditional Fourier Optics. The possibilities of SPP focusing using in-plane traditional FZP was demonstrated in [6].
Figure 1 represents an adaptation of a free-space quasioptical component known as the 3D Fresnel zone plate (conical FZP) for focusing SPP waves.
A conventional free-space flat conical FZP comprises quasi-concentric structure. From the geometric consideration for the FZP on a cone surface the boundaries (a,y) of n-th zone is determined from the quadratic equation [5]:
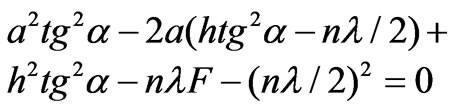 (1)
(1)
 , (2)
, (2)
where (a,y) is function of the n, h – the height of the cone.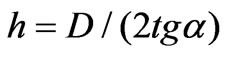 , D – is the diameter of the FZP. The design of flat cone FZP is based on a phase modulation of the surface plasmon provided by dielectric block deposited on the interface. The modulation can be realized by changing height or width of the dielectric block. We compare the focusing properties of the flat FZP, and the cone FZPs with different h=(F/3, F/2, F-10
, D – is the diameter of the FZP. The design of flat cone FZP is based on a phase modulation of the surface plasmon provided by dielectric block deposited on the interface. The modulation can be realized by changing height or width of the dielectric block. We compare the focusing properties of the flat FZP, and the cone FZPs with different h=(F/3, F/2, F-10 ). The diameter of the FZP lenses is 30 mm with a focal length of F=2.5 cm at 1 THz.
). The diameter of the FZP lenses is 30 mm with a focal length of F=2.5 cm at 1 THz.
Planar diffractive elements have a number of specific features [5,13–14], the main of them being: one-dimen-

Figure 1. Diffractive planar element on a conical surface
sional nature of the element and the need to take into account the properties of the substrate on which the element is placed. From the mathematics standpoint, the first of these factors is easy to take into account: for this, integration over angle in calculating the diffraction integral is replaced with a sum of two values of the integral for j = 0 and j = p (in the symmetric case). In other words, it is not necessary to compute the double integral but the sum of two single integrals.
Thus, for the planar analogue of the zone plate it will be sufficient to calculate the sum of two single integrals of the following type [5]:
U(p2) =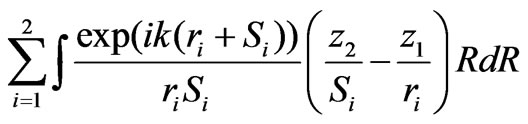 where p2 = (х2,0,z2) are the coordinates of the observation point; p1 = (х1,0,z1) are the coordinates of the radiation source;
where p2 = (х2,0,z2) are the coordinates of the observation point; p1 = (х1,0,z1) are the coordinates of the radiation source;
А = -z1; B = z2; r21 = (z1 - z)2 + (x1 - R)2;
S21= (z2 - z1)2 + (x2 - R)2
and r22 = (z1 - z)2 + (x1 + R)2;
S22 = (z2 - z)2 + (x2 + R)2.
The frequency and focusing properties of diffractive elements fabricated on a curvilinear surface are determined, among other things, by the degree of convexity (concavity) of the surface. We can expect, therefore, that placing of planar elements of integral optics on non-flat curves will provide the possibility of controlling both the frequency and the focusing properties. As an example, consider the main properties of a “conical” diffractive element (Figure 1) [5]. The initial data for such “planar conical” diffractive element were: D/l ~ 35, D/A ~ 0.4, D/B ~ 0.8; the number of phase quantization levels was two; the element of phase inversion type was chosen. Its pro-perties were investigated numerically and experimentally in the 4 mm wavelength band.
3. Experimental and Simulation Results
The method of computing simulation is described in detail in the book [5]. The detailed description of experimental set-up and the technique of researches are also described in [5].
Figure 2 shows the distribution of field intensity in the focal region of a diffractive element transversally to its optical axis; it was obtained experimentally and by numerical computation of the diffraction integral. The transition from three-dimensional element to two-dimensional structures increases the level of side lobes. Further investigation of the properties of such elements showed that the frequency and focusing properties are maintained in a wide spectral interval, just as they are for three-dimensional diffractive elements. As it follow from the Figure 2, the proposed focusing element allow to focus SPP with limiting space resolution according Airy criterion [5].
Therefore, the investigation of the planar two-dimensional diffractive element fabricated on a conical surface and a comparison of the results obtained with the characteristics of similar three-dimensional diffractive elements (Figure 3) allow us to draw a conclusion that such planar elements possess adequate frequency characteristics, sustain focusing ability in a wide spectral range on wavelengths that differ from the nominal wavelength, and are diffraction-constrained systems. It could be noted that the focal length of the conical FZP is less influenced by changes in air-gap, i.e., a change in the effective refractive index, since the focal length is mainly determineed by the spatial diffractive profile, which is fixed. The confined field distribution is characterized in detail by the method of Finite-Difference Time-Domain (FDTD). Calculations were performed by the software package, XFDTD 6.2, from REMCOM.
Also we have shown that an air-gap control of a floating dielectric block can generate the dynamic phase and amplitude modulation of the SPP transmission coefficient. As an application of this property, we have demonstrated the variable-focusing properties of an SPP floating dielectric parabolic lens using numerical simulations and compared the focusing properties of SPP parabolic lenses and SPP Fresnel lenses. Unlike conventional bulk optics,

Figure 2. Field intensity distribution transversally to the optical axis of a planar diffractive element: __________theory; _ _ _ _ _ experiment
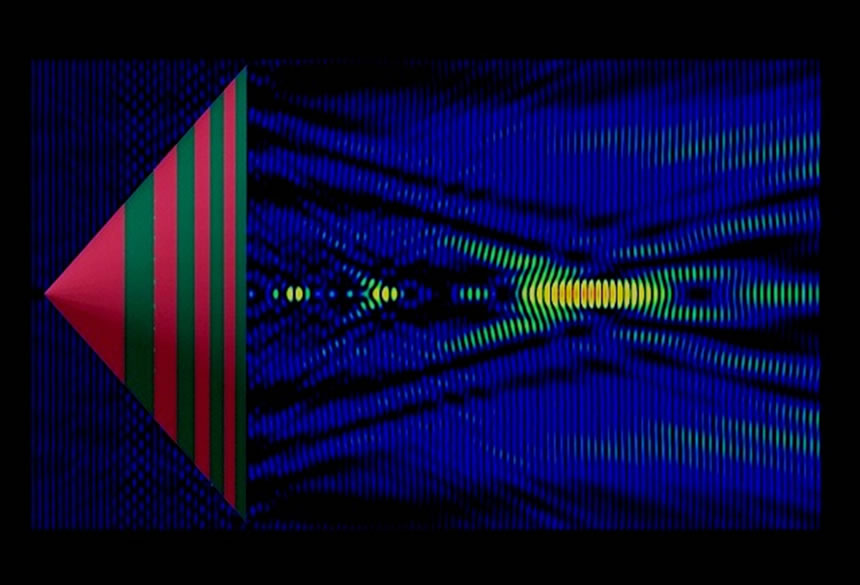
Figure 3. The field intensity distribution along the optical axis of 3D conical FZP calculated by FDTD method
the nano-scale surface optics for SPP processing contains several unexpected and interesting features in addition to the physical features described in this paper. Dynamic plasmonic information processing on the nano-scale using air-gap control may be an effective mechanism for building a dynamic plasmonic information processing system.
4. Conclusions and Discussion
The successful adaptation of free-space 3D conical Fresnel Zone Plate for operation on SPP waves demonstrates that analogues of Fourier diffractive components can be developed for SPP 3D optics. As in free-space, the basic SPP optical components are the necessary enablers for more sophisticated future devices.
So we have demonstrated that analogs of diffractive and refractive 3D optics in free space can be developed to manipulate surface waves such as SPPs and focusing electromagnetic waves with diffraction limit.
The possibility of manipulating SPP-like light beams, but in 2D and 3D, will provide many new possibilities. For example, the implementation of optical digital computers mostly depends on the creation of optical logic elements (optical analogues of electronic gates) that carry out various logical operations (AND, OR etc) that would go beyond the speed of microelectronic devices and their degree of integration, also reducing cost and power consumption [5,13,14]. Diffractive (dispersive) elements can be used for spectrally selective addressing of signals, can be applied in polychromatic optical processors, serve as a basis for polychromatic logic elements or multiplexer or a focusing element with selectivity in the multimode regime etc. [5]. It has been shown by detailed simulation results obtained using a parallel FDTD method that novels diffractive element in the THz waveband offers the potential to realize novel types of devices for communications, sensing, integrated optics, networks, transmission lines, and so on [15–18]. To this end, diffractive planar elements fabricated on non-flat surfaces make it possible to enrich the “pool of devices” for applications including integrated optics at different waveband, including THz, and to design elements with novel properties and potentials.
Another application of new SPP 3D FZP is to focusing surface plasmon polariton trapping of colloidal particles. The in-plane 3D FZP focus area releases a significant amount of energy to the liquid, particularly in the center region where an enhancement of the near-field intensity is observed. Thus, the localized convection streams, which result from this off-equilibrium process, are enhanced when the SPP resonates. The resulting contrast leads to an in-plane electromagnetic intensity gradient, which can be engineered to form a stable potential well able to trap particles located in its vicinity.
REFERENCES
- X. Wu, D. Li, W. H. Sun, F. Gao, Z. J. Zhang, and R. W. Peng, “Coupling of terahertz surface plasmon polaritons in corrugated stacks of dielectric and semiconductor,” PIERS Online, Vol. 5, No. 2, pp. 101–104, 2009.
- M. Rajarajan, C. Themistos, B. M. A. Rahman, and K. T V Grattan, “Plasmonics in metal-clad terahertz waveguides,” PIERS Online, Vol. 3, No. 3, pp. 294–299, 2007.
- J. G. Han, X. C. Lu, A. K. Azad, M. F. Gong, and W. L. Zhang, “The role of non-resonant effect in terahertz transmission through subwavelength holes,” PIERS Online, Vol. 4, No. 4, pp. 481–484, 2008.
- S. C. Chen, T. M. Chang, and D. P. Tsai, “Focusing the enhanced near-field by manipulating the nano-plasmon-driving intensifiers,” PIERS Online, Vol. 1, No. 4, pp. 445–447, 2005.
- I. V. Minin and O.V. Minin, “Diffractional quasioptics,” Moskow: InformTei, pp. 180 (in Russian), 1992. See also: O. V. Minin and I. V. Minin, “Diffraction optics of millimeter waves,” London: IOP Publisher, pp. 396, 2004.
- L. Feng., K. Tetz, B. Slutsky, V. Lomakin, and Y. Fainman, “Fourier plasmonics: Diffractive focusing of in-plane surface plasmon polarition waves,” Applied Physics Letters, 91, 081101, 2007.
- Schatz G. C. and R. P. van Duyne (Eds.), “Electromagnetic mechanism of surface-enhanced spectroscopy,”
- Wiley, New York, 2002.
- R. F. Wallis and G. I. Stegeman (Eds.), “Electromagnetic surface excitations,” Springer Series on Wave Phenomena, Springer, Berlin, 1988.
- D. B .Ostrowsky and R. Reinisch (Eds.), “Guided wave nonlinear Optics,” Kluwer Academic Publishers, Dordrecht, 1992.
- I. P. Radko, S. I. Bozhevolnyi, A. B. Evlyukhin, and A. Boltasseva, “Surface plasmon polariton beam focusing with parabolic nanoparticle chains,” Opt. Express 15, 6576–6582, 2007.
- W. Nomura, M. Ohtsu, and Yatsui T, “Nanodot coupler with a surface plasmon polariton condenser for optical far/bear-field conversion,” Applied Physics Letters, 86, 181108, 2005.
- R. Zia and M. L. Brongersma, “Surface plasmon polariton analogue to Young’s double-slit experiment,” Nature Nanotech, 2, pp. 426–429, 2007.
- I. V. Minin, O. V. Minin, C. Chen, J. Mititu, and D. W. Prather, “Novel type of the elements of integrated diffractive optics,” Terahertz for Military and Security Applications IV, Novel Terahertz Devices and Concepts III. Proc. SPIE 6212, pp. 17–21, April 2006, Gaylord Palms Resort and Convention Center Orlando (Kissimmee), Florida, USA
- I. V. Minin, O. V. Minin, D. Prather, S. Shi, “The potential of flat curvilinear DOE as a key element of future integrated diffractive optics and information protected element,” In Proceeding of the 5th IEEE-Russia Conference “Microwave electronics: measurements, identification, applications,” MEMIA 2005, pp. 13-15, December 2005, Novosibirsk, Russia, pp. 186–193.
- Y. Y. Feng and M. Willatzen, “Plasmonic effects in dynamic tunable metal-dielectric composites,” PIERS Online, Vol. 4, No. 6, pp. 625–630, 2008.
- R. Blaikie, L. Lin, and R. Reeves, “Surface-plasmonenhanced optical transmission through planar metal films,” PIERS Online, Vol. 1, No. 6, pp. 634–637, 2005.
- T. Suyama, Y. Okuno, and T. Matsuda, “Plasmon resonance-absorption in a metal grating and its application for refractive-index measurement,” PIERS Online, Vol. 1, No. 6, pp. 659–663, 2005.
- P. Wang, X. J. Jiao, L. Tang, D. G. Zhang, Y. H. Lu, J. P. Xie, and M. Hai, “A planar metallic collimator based on controlling surface plasmons's phase,” PIERS Online, Vol. 1, No. 3, pp. 369–371, 2005.

