Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 11 (2012) , Article ID: 24685 , 11 pages DOI:10.4236/ijcns.2012.511081
On the Computing of the Minimum Distance of Linear Block Codes by Heuristic Methods
SIME Lab, National School of Computer Science and Systems Analysis (ENSIAS), Mohammed V-Souisi University, Rabat, Morocco
Email: askali11@gmail.com
Received August 27, 2012; revised September 30, 2012; accepted October 8, 2012
Keywords: Minimum Distance; Error Impulse Method; Heuristic Methods; Genetic Algorithms; NP-Hardness; Linear Error Correcting Codes; BCH Codes; QR Codes; Double Circulant Codes
ABSTRACT
The evaluation of the minimum distance of linear block codes remains an open problem in coding theory, and it is not easy to determine its true value by classical methods, for this reason the problem has been solved in the literature with heuristic techniques such as genetic algorithms and local search algorithms. In this paper we propose two approaches to attack the hardness of this problem. The first approach is based on genetic algorithms and it yield to good results comparing to another work based also on genetic algorithms. The second approach is based on a new randomized algorithm which we call “Multiple Impulse Method (MIM)”, where the principle is to search codewords locally around the all-zero codeword perturbed by a minimum level of noise, anticipating that the resultant nearest nonzero codewords will most likely contain the minimum Hamming-weight codeword whose Hamming weight is equal to the minimum distance of the linear code.
1. Introduction
The Minimum distance of a linear error correcting code has a practical and theoretical interest. It provides a great deal of information on the code capability in detecting and in correcting errors or erasures.
Since, to date, these problems cannot be solved mathematically because it is in general a NP-hard problem, it becomes necessary to physically search the codewords of a code in order to find the codeword with the minimum weight. Unfortunately, as the size of the code increases, the size of the search space becomes prohibitively large. The number of information bits in a code, k, defines the size of a search space. Note that k is also the number of basis vectors in the code and thus the size of the search space is 2 k. Thus, an exhaustive search is not feasible, but a heuristic search may provide valuable information and, in some cases, perhaps a solution. We propose several different algorithms and heuristic search techniques such as Genetic Algorithm (GA) [1-4], and search local error using a Soft-In decoder when applied to the problem of determining the true minimum distance of a linear block code [5].
In the past, many excellent studies have found the minimum weight for Quadratic Residue (QR) codes or its extended codes were presented in [6-10], in [11] we have estimated the minimum distance of Double Circulant Codes (DCC) using genetic algorithm, and Wallis et al. [12] have presented a different genetics techniques applied to find an estimate of the minimum distance for some Bose-Chaudhuri-Hocquenghem (BCH) codes, In [13], Nouh et al. have used genetic algorithms for finding a likelihood weight enumerator of some linear block codes, in particular their minimum weights.
Other works interest to the distance measurement methods have been introduced: Garello’s true distance spectrum method [14], Berrou’s error-impulse method [15], Garello’s all-zero iterative decoding method [16] and Crozier’s double (and triple) impulse method(s) [17].
Furthermore, there are also other works [18-20] based on artificial intelligence, trying to solve problems related to coding theory.
In this paper, we deal with finding a good estimate of minimum distance of linear block codes using genetic algorithms to BCH, QR, and DCC codes and which we denote dt, and we compare our results to previous works. Finally, we present results obtained by using our search local error method published in a previous work [5], where we use a Soft-In Ordered Statistics decoder (OSD).
The remainder of this paper is organized as follow: in Section 2, we introduce the genetic algorithms; Section 3 describes the proposed heuristic methods to find a tight minimum distance, Section 4 reports the simulation results and discussions. Finally, Section 5 presents the conclusion and future trends.
2. Genetic Algorithms
Genetic Algorithms was first proposed by John Holland’s, as a means to find good solutions to problems that were otherwise computationally intractable. Holland’s schema theorem [21], and the related building block hypothesis, provided a theoretical and conceptual basis for the design of efficient GA. It also proved straight forward to implement GA due to their highly modular nature. As a consequence, the field grew quickly and the technique was successfully applied to a wide range of practical problems in science, engineering and industry. GA theory is an active and growing area, with a range of approaches being used to describe and explain phenomena not anticipated by earlier theory. In tandem with this, more sophisticated approaches for directing the evolution of a GA population are aimed at improving performance on classes of problem known to be difficult for GA, [21]. The development and success of GA contributed greatly to a wider interest in computational approaches based on natural phenomena. It is now a major stand of the wider field of computational intelligence, which encompasses techniques such as neural networks, and artificial immunology. Genetic algorithms are search methods that can be used for both solving problems and modelling evolutionary systems.
Since it is heuristic (it estimates a solution), GA differs from other heuristic methods in several ways. The most important difference is that it works on a population of possible solutions, while other heuristic methods use a Another important difference is that GA is not a deterministic but a probabilistic one.
A genetic algorithm is defined by (see Figure 1):
Individual or chromosome: a potential solution of the problem, it’s a sequence of genes.
Population: a set of points of the research space.
Environment: the space of research.
Fitness function: the function to maximize/minimize.
Encoding of chromosomes: it depends on the treated problem, the famous known schemes of coding are: binary encoding, permutation encoding, value encoding and tree encoding.
Stochastic Operators:
• Selection: replicates the most successful solutions found in a population at a rate proportional to their relative quality.
• Crossover: Decomposes two distinct solutions and then randomly mixes their parts to form novel solutions.
• Mutation: Randomly perturbs a candidate solution. In the selection process, some individuals are selected to be copied into a tentative next population. Individual with higher fitness value is more likely to be selected. The selected individuals are altered by the mutation and crossover and form a new population of solutions. The GA is simple yet provides an adaptive and robust optimization methodology [22].
3. Estimation Methods for Finding the Minimum Distance
3.1. Methods Based on Genetic Algorithms
In the sequel of this paper, we use the following nota-
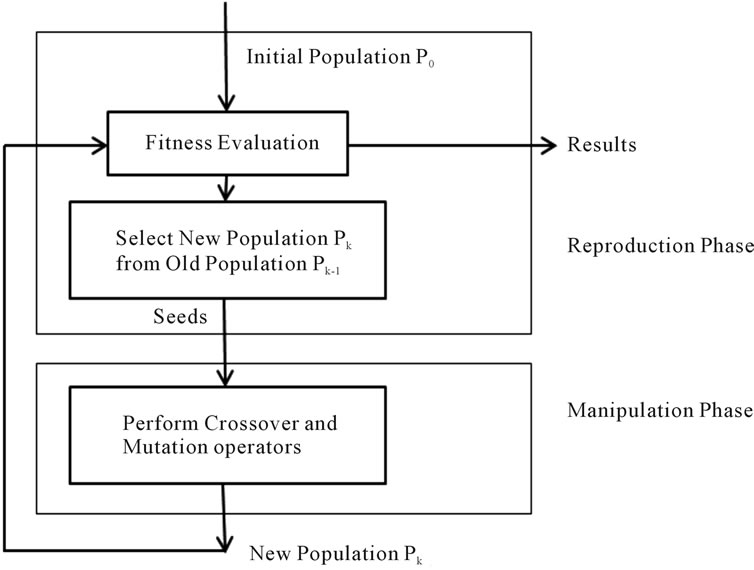
Figure 1. The basic structure of the genetic algorithm.
tions:
• Ni the cardinal of the population.
• Coding the encoding function.
• Ng the number of generations.
• Ne the number of elites (better parents).
• Ngmax is the maximum number of generations and C(I) is the codeword obtained by coding the information vector I.
In order to use genetic algorithms, in our work, we use binary encoding which consists to treat an individual as a binary sequence. We proposed Two GA variants A and B.
3.1.1. Genetic Algorithm: Variant A
This algorithm permits to find a minimum weight in a linear code C. It is known in field of coding theory that there exists always a linear systematic code equivalent to C. For the purposes of this paper we suppose that the generator matrix G of the code C is systematic; this chose permits to initialize the initial population by words of weight less than the global upper bound corresponding to the length n and the dimension k. the algorithm expects as inputs the probability of mutation pm of a single bit, and the crossover probability pc.
• Algorithm Steps
The steps of the algorithm are organized as follow:
Step 1: randomly generate an initial population
Seed uniformly, randomly the initial population with a Ni, and where each individual is a word of length k with a random weight. We initiate the number of generation Ng to 1.
Step 2: while (Ng < Ngmax) do
Step 2.1: Compute the fitness of each individual in the population
An individual i represents an information vector of k bits which is encoded by the code generator to an n-bit code vector. The fitness is the weight of the encoded individual if this last is different to zero otherwise, the fitness is equal to n as a maximum value.
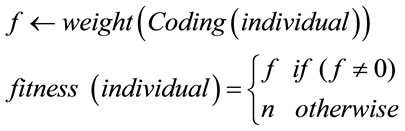
Step 2.2: Sort population in increasing order of fitness
Step 2.3: Insert the best Ne = 50% individuals in the intermediate population
Step 2.4: For i = Ni/2 to Ni
Step 2.4.1: Randomly select two individuals p1 and p2 for reproduction
Step 2.4.2: 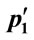 = mutate (p1) and
= mutate (p1) and 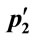 = mutate (p2): Flip each bit of p1 and p2 with probability pm
= mutate (p2): Flip each bit of p1 and p2 with probability pm
Step 2.4.3: Cross (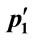 ,
,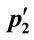 ) with probability pc to produce two children ch1 and ch2
) with probability pc to produce two children ch1 and ch2
Step 2.4.4: f1 ( weight (Coding (ch1)); f2 ( weight (Coding (ch2))
Step 2.4.5: if (f1 < f2) then insert ch1 in the intermediate population else insert h2
End For
End while
Step 3: output the first individual in the last population
• Description of the Algorithm
In this entire paper, the crossover and the mutation stochastic operators operate only on the information bits represented as k-dimensional vectors. An alternative strategy is to represent individuals as n bit codewords.
In Step 2.1, to evaluate the fitness of an individual, it is necessary to first encode it by multiplying it with generator matrix G or by the generator polynomial if the code is cyclic as in some cases of our study. If the weight of the encoded vector is not null, the fitness is equal to weight (Coding (vector)) otherwise the fitness is equal to n. An individual is better than another if its weight is the smallest.
In Step 2.2 and Step 2.3, we use a Linear Ranking Selection strategy where individuals in population are sorted by non-decreasing order of weight of encoded individual vector, and we select the best Ne = 50% individuals to yield the intermediate population.
In Step 2.4, we use a single crossover point strategy, in which both parents organism strings is selected. All data beyond that point in either organism string is swapped between the two parents organisms. The resulting organisms are the children (see Figure 2).
Concerning selection, we use the random selection, in that only Ne individuals are preserved in the next generation, and we select randomly two parents to reproduce a best offspring that is more likely to contain good schema. The mutation step is done bit-wise on offspring with probability pm.
3.1.2. Genetic Algorithm: Variant B
• Algorithm Steps
The steps of the algorithm are organized as follow:
Step 1: randomly generate an initial population
Seed uniformly, randomly the initial population with a Ni, and where each individual is a word of length k with a random weight. We initiate the number of generation Ng to 1.

Figure 2. The single crossover structure.
Step 2: while (Ng < Ngmax) do
Step 2.1: Compute the fitness of each individual in the population
An individual i represents an information vector of k bits which is encoded by the generator code to an n-bit code vector. The fitness is the weight of the encoded individual if this last is different to zero otherwise, the fitness is equal to n as a maximum value.
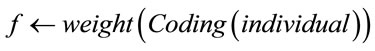
Step 2.2: Sort population in increasing order of fitness
Step 2.3: select the best Ne individuals in the intermediate population
Step 2.4: i = Ne to Ni
Step 2.4.1: tournament select of two parents p1 and p2 for reproduction
Step 2.4.2: If (rand_value < pc) {Cross p1 and p2 to generate ch1 and ch2; Mutate ch1 and ch2 and introduce them in the next population} Else introduce p1 or p2 into the next population with equal probability.
End For
Step 2.5: Let currbest = fittest of the intermediate population. If (fitness (best) < fitness (currbest)) best = currbest
End while
Step 3: output best
• Description of the Algorithm
There are many differences between variant A and this variant in strategies of selection, order of stochastic operators, and the method of offspring reproduction.
In Step 2.4.1, we use the tournament selection, in that only one of two possible parents is preserved to reproduce two children whose will be inserted in the next generation.
Step 2.4.2, in this variant, the crossover operation depends on pc, and it is done before the mutation step which is done bit-wise on offspring with probability pm. In case of no-cross we insert the two initials parents in the next generation. We have used three strategies of crossover: a single crossover point (depicted in Figure 2), two point crossover, and uniform crossover. The twopoint Crossover that randomly selects two crossover points within a chromosome then interchanges the two parent chromosomes between these points to produce two new offspring (see Figure 3). The Uniform Crossover uses a fixed mixing ratio between two parents. Unlike oneand two-point crossover, the Uniform Crossover enables the parent chromosomes to contribute the gene level rather than the segment level. An example of this operation is depicted in Figure 4.
3.2. A New Algorithm Based on Error Impulse Method
This method is not based on the analysis properties of the
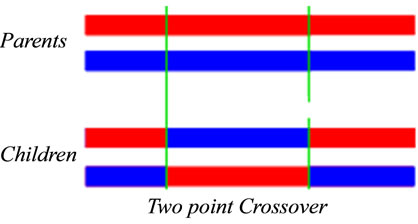
Figure 3. Two-point crossover structure.

Figure 4. Uniform crossover structure.
code but on the correction capability of the decoder. To obtain a good estimate of the minimum distance of a code, it is critical to apply a noise as possible to the all-zero codeword, so that the noise energy brings the decoder marginally away from the all-zero codeword.
The nature of the noise is so important, and it depends on the decoder used, for this, Berrou has proposed in [15] the Error impulse Method to excite the MLD decoder for turbo codes, and Xiao et al. [23] has proposed the Bit Reversing to excite the iterative decoder IRB proposed by Fossorier for LDPC codes. Another recent approach, by Garello et al. [24], is called the “all-zero iterative decoding algorithm”. Here, this approach will be referred to as the “single impulse method” for reasons that will become apparent. This approach is similar to the error impulse method in that an impulse is again placed at a specific data index in the all-zero codeword. The main difference is that the amplitude of the impulse is intentionally set very high so that the decoder cannot correct it, but rather is forced to converge to (or at least select) a non-zero data pattern.
We denote by 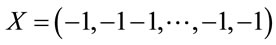 the word associated to the “all-zero” codeword modulated by the BPSK.
the word associated to the “all-zero” codeword modulated by the BPSK.
3.2.1. Berrou’s Algorithm
The noise pattern proposed by Berrou et al. in [15] called Error Impulse, which was originally proposed for computing the minimum distance of Turbo codes.
In [15] C. Berrou developed and justified an algorithm with the MLD decoder to compute the minimum distance especially for Turbo codes, the principle of the idea is to send an “all-zero” codeword and adding gradually the level of noise and watch the capability of the decoder to return the “all-zero” codeword. Otherwise, this approach is based on inserting a (low-amplitude) error impulse into the all-zero codeword at a specific data index to see if the Turbo decoder can correct it. The amplitude of the error impulse is increased until the decoder fails. The highest amplitude that could be corrected provides an estimate of the minimum distance associated with that specific data index. An estimate of the overall minimum distance is obtained by testing all of the data indices in this manner. It was shown in [15] that this approach is guaranteed to find the true dt if the decoder is a true maximum likelyhood (ML) decoder. Of course, Turbo decoders are not true ML decoders. Thus, there is no guarantee that the error impulse method will find the true dt. Further, although this approach is usually pessimistic, there is no guarantee that the result will be a true lower bound on dt.
3.2.2. The Proposed Multiple Impulse Method (MIM)
The proposed algorithm produces a tight minimum distance based on true (low-weight) codewords found by a fine-tuned local search.
We assume that dt is in the range [d0, d1] where d0 and d1 are two integers. Then dt can be determined as follows:
Step 1: set Amin = d1 + 0.5 and dt = n − k1; nb_test.
Step 2: For i = 1 to nb_test
Step 2.1: A = d0 – 0.5;
Step 2.2: Set [(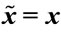 ) = TRUE];
) = TRUE];
Step 2.3: While [(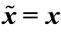 ) = TRUE] & [A ≤ Amin – 1.0]
) = TRUE] & [A ≤ Amin – 1.0]
Step 2.3.1: A = A + 1.0
Step 2.3.2: For nb_error = error_max to 1
Step 2.3.3: Subdivide A randomly on nb_error positions
Step 2.3.3.1: OSD decoding of Y →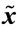
Step 2.3.3.2: If (weight (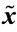 7925 />) ≤ dt) then dt = weight (
7925 />) ≤ dt) then dt = weight (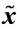 )
)
Step 2.3.3.3: If (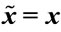 ) then [(
) then [(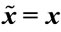 ) = TRUE]
) = TRUE]
End for
End while
Step 2.4: Amin = A;
End for
Output: dt is the minimum distance
We changed the Soft-In MLD decoder used in Berrou’s [15] Algorithm by a Soft-In OSD decoder which is very fast, by injecting a noise iteratively in a random positions, the decoder word will be mostly near than the “all-zero” codeword, and the minimum distance of the code will be the minimum weight of the decoded words and is not the magnitude 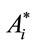 of the noise as we have in Error Impulse Method.
of the noise as we have in Error Impulse Method.
4. Results and Discussions
4.1. Parameters Optimization of Genetic Algorithms
In Tables 1-4, we analyze the impact of genetic operators on the minimum distance.
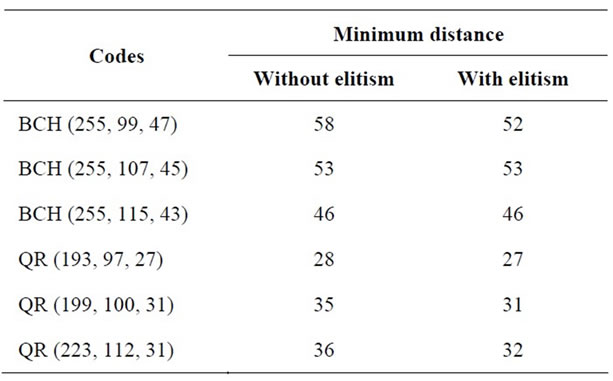
Table 1. Effect of elitism operator.
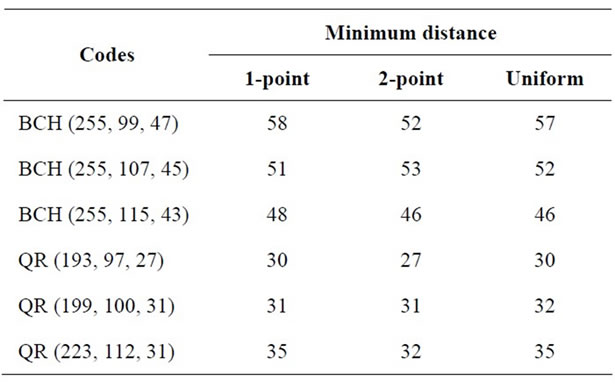
Table 2. Effect of crossover operator types.
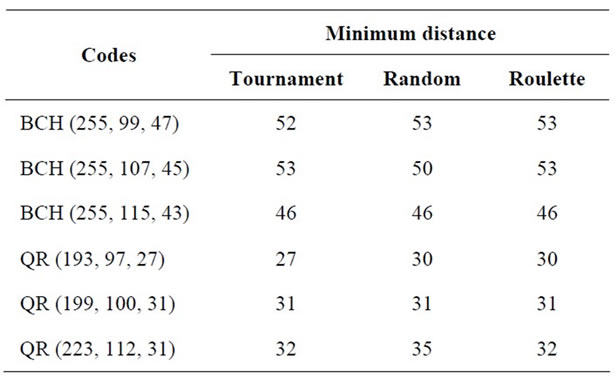
Table 3. Effect of selection types.
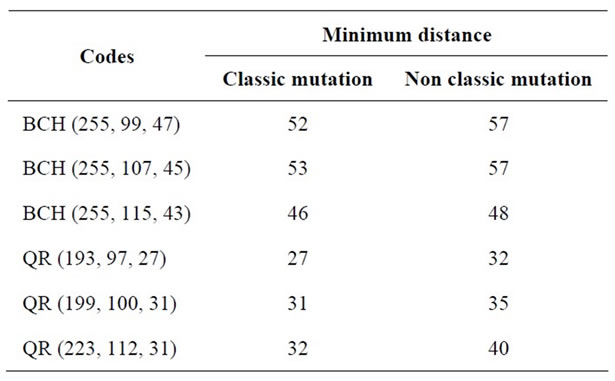
Table 4. Effect of mutation operator types.
4.1.1. Effect of Elitism
It appears that elitism significantly improves the performance of genetic algorithm for QR codes and BCH codes.
4.1.2. Effect of Crossover
These results explain that 2-point crossover seems to perform significantly better than uniform and 1-point crossover for QR codes and BCH codes.
4.1.3. Effect of Selection
As shown results in the Table 3, in general, the tournament selection gives a very close upper bound to the minimum distance for QR codes and BCH codes.
4.1.4. Effect of Mutation
In this paragraph, we compare the impact of the classic mutation with other type of mutation. This last alters an individual by bit inversion of chromosome. However, such an inversion takes place only in one bit and only when an improvement in the individual’s fitness is achieved. If it is not possible to improve the individual‘s fitness, then no alteration is performed. The algorithm simply goes through every chromosome’s gene to determine which of them must be changed in such a way as to improve individual’s fitness.
According to the results of this study, we concluded that the best parameters for this algorithm are: Elitism operator, tournament selection, 2-point crossover, and classical mutation.
4.2. Results of Various Genetic Algorithms
All simulations were made with default GA parameters outlined in the Table 5.
The Table 6 shows that the proposed algorithms out
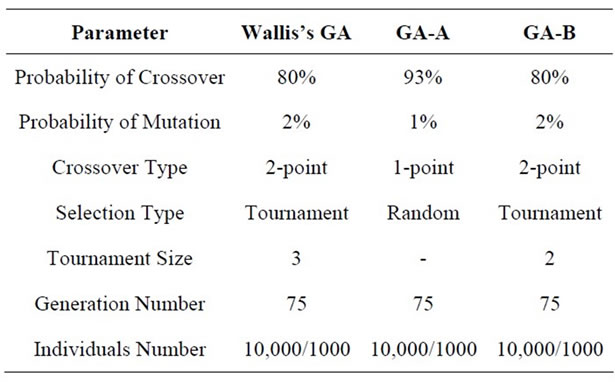
Table 5. Parameters of implementation of genetic algorithms.
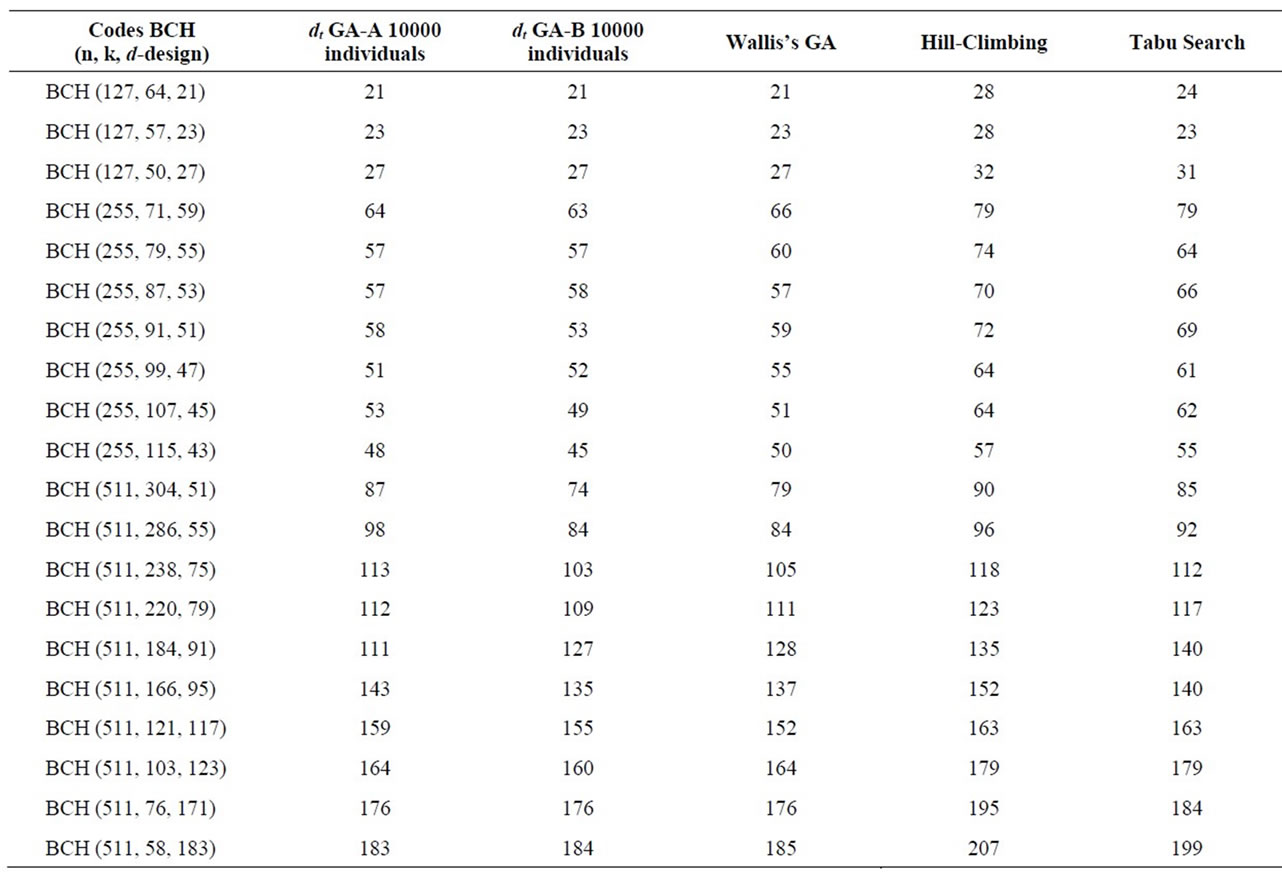
Table 6. Comparaison of our GA algorithms with other works for some BCH codes.
performed the other optimization techniques.
The Table 7 shows the computational results of minimum distance via GA-A, GA-B, and the Simulated Annealing (SA) developed by authors in [25].
In the Table 7, for the three first BCH codes listed, these algorithms found the true minimum distance. However, for the two last BCH codes, the gap between the minimum distance obtained by the SA algorithm and the true value is still large, while our genetic algorithms found this true minimum distance.
The Table 8 shows that our two variants of GA give the same estimate of the minimum distance for Quadratic residue codes where the length is less than 223.
The Table 9, we validate our estimate minimum distance by the exhaustive method for some random DCC defined by their binary header.
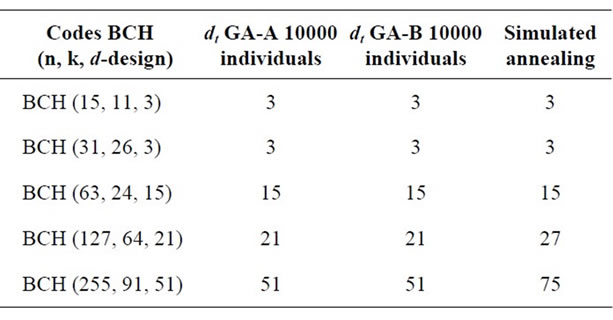
Table 7. Comparaison between our two GA variants with simulated annealing.
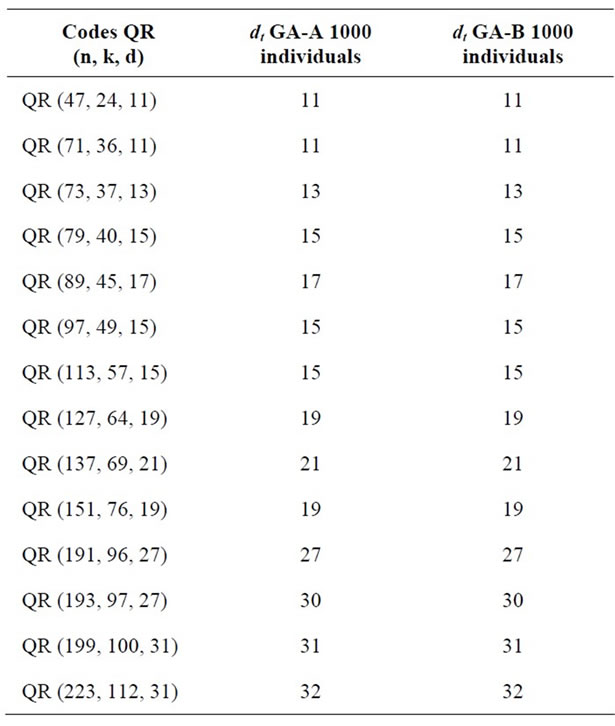
Table 8. Comparaison between our two variants applied to QR codes.
4.3. Validation and Results of Multiple Impulse Method
4.3.1. Validation of the Multiple Impulse Method
All simulations have been done using a simple configuration machine: Intel® CoreTM 2 CPU T5600 @ 1.83 GHz, RAM: 2.00 GHz.
As a first step, we validated the algorithm by verifying the minimum distance for some linear codes: BCH codes, Quadratic residue Codes, and Quadratic Double-Circulant Codes in their Bordered form, for which the minimum distance is known.
The results are summarized in the Tables 10-12, in which “OSD_EI” denotes the Order Statistic Decoding with Error impulse and “TTE” denotes the Time of execution in seconds. As it is shown in these tables our algorithm is successfully validated.
Let p be a prime that is congruent to ±3 modulo 8. A binary [2(p + 1), p + 1] quadratic double-circulant code (QDC) [26], denoted by B, can be constructed using the following defining polynomials:
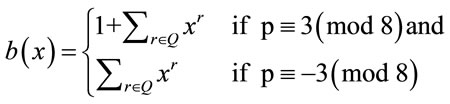 (1)
(1)
Q is the set of quadratic residues modulo p.
The generator matrix G of B can be written as described in Figure 5.
We find exactly what Tomlinson has found in [26].
4.3.2. New Experimental Results
In this section we present an application of the proposed algorithm to find the true unknown minimum distance of some residue quadratic codes (QR and QDC see Tables 14-16) and some BCH codes (see Table 13) comparing respectively to some known upper bounds, and to the designed distance or comparing to the Grassl table [27].
By MacWilliams and Sloane in [28], for QR codes, we compare our estimation by this inequality 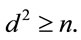
By the Pless’s identity [29], the minimum weight in Quadratic Residue codes is always odd. This means that when we find a codeword with a pair weight w, it is necessary to have a codeword with an odd weight w-1.
In the Table 14 we give some QR codes where the length is like the form n = 8 m + 1.
In our knowledge the Krasikov Bound [30] is the best upper bound for comparing our estimation of the minimum distance. In the Table 15 we give some QR codes
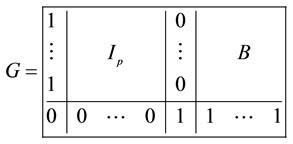
Figure 5. The quadratic double circulant form.
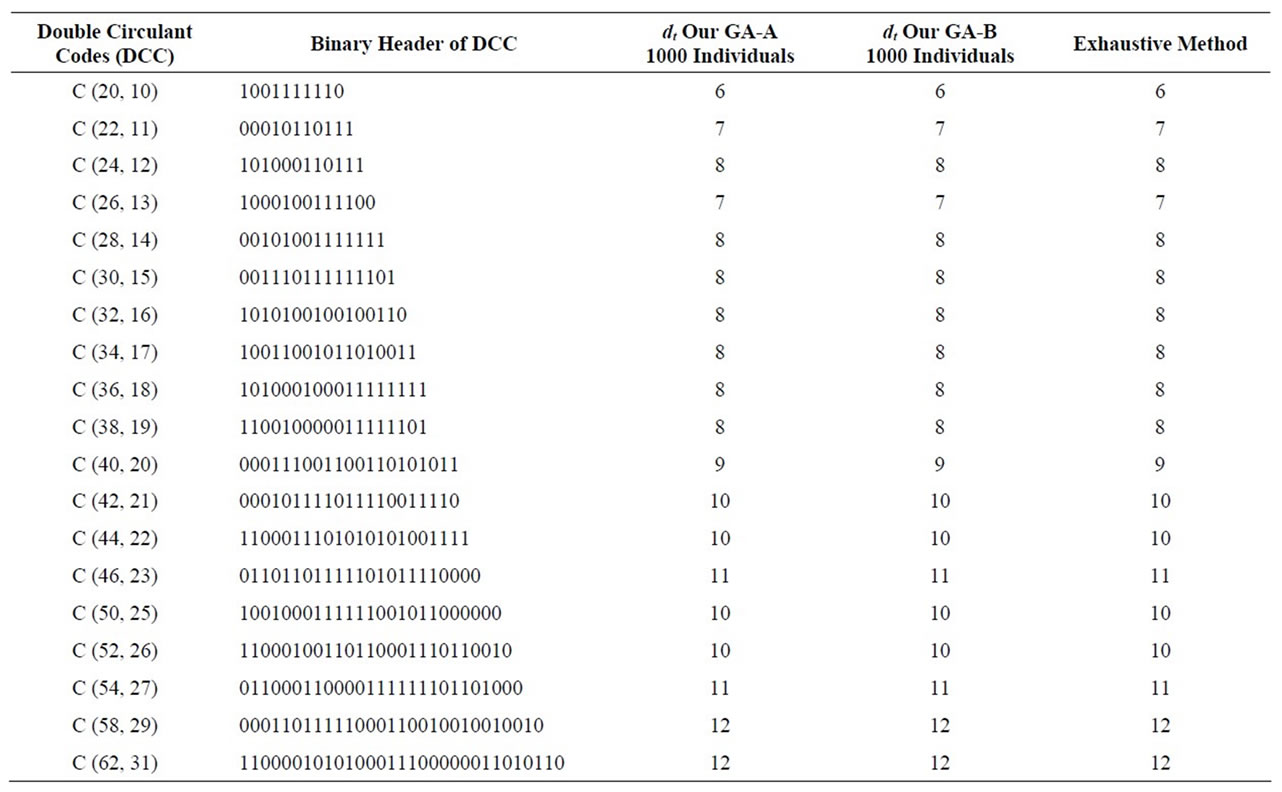
Table 9. Comparaison between our two variants applied to QR codes.
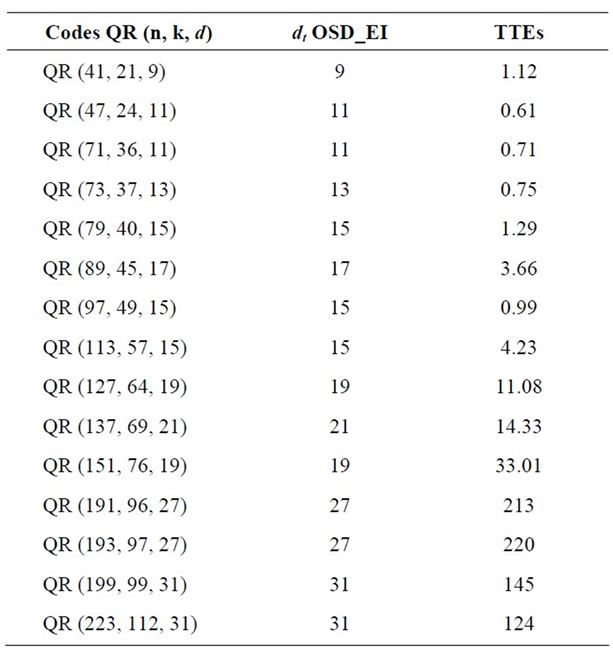
Table 10. Validation of some QR codes with known minimum distance.
where the length is like the form n = 8m − 1, and we have: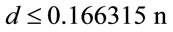 .
.
For the class of QDC codes we give in the next table some codes with unknown minimum.
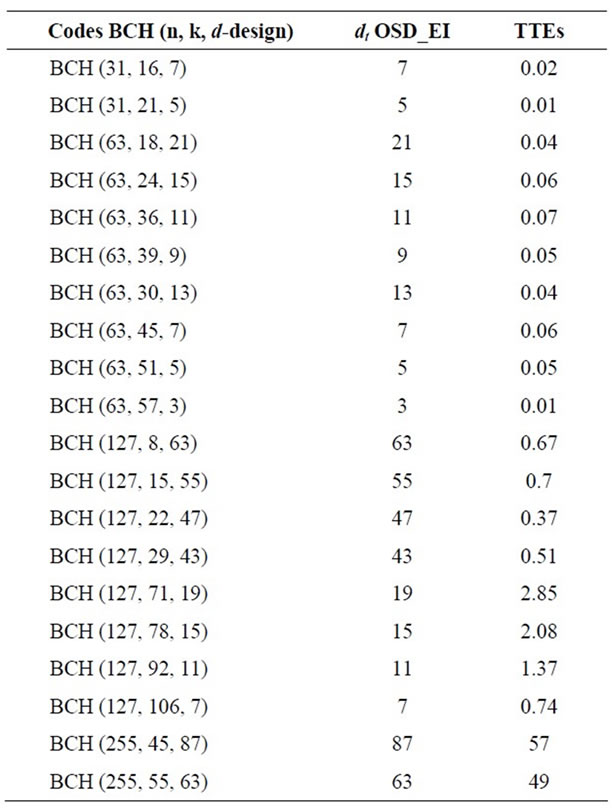
Table 11. Validation of some BCH codes with known minimum distance.
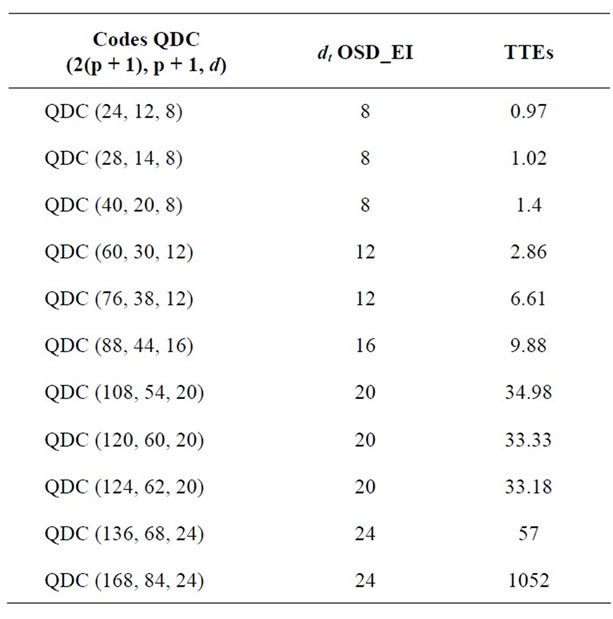
Table 12. Validation of some QDC codes with known minimum distance.
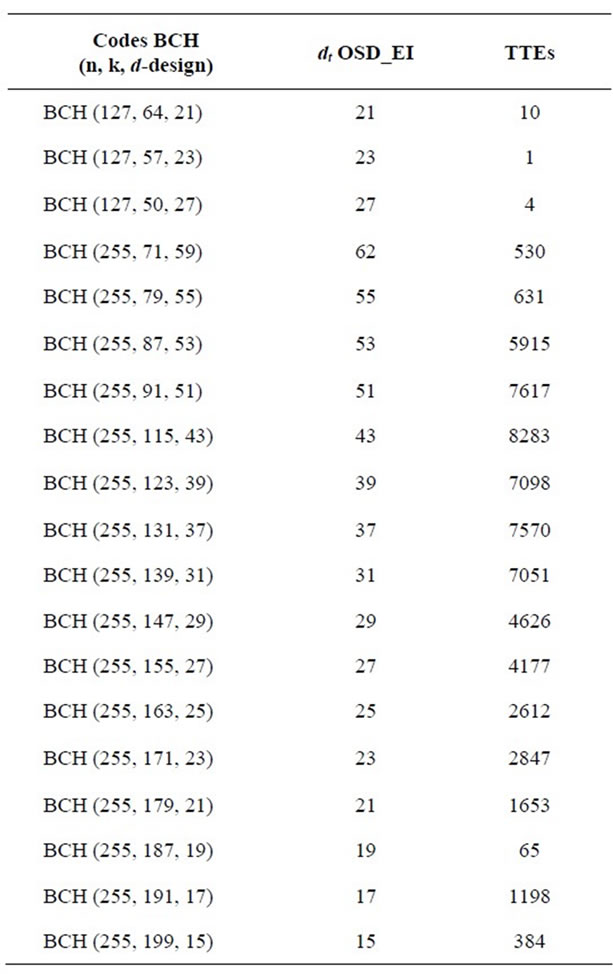
Table 13. Tight bound for unknown minimum distance of some BCH codes.
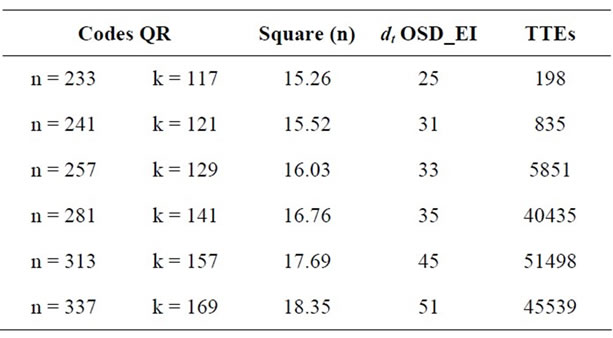
Table 14. Tight bound of the unknown minimum distance of some QR codes.
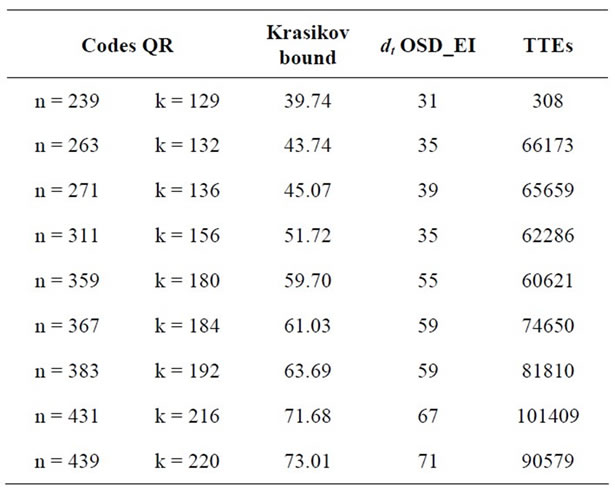
Table 15. Tight bound of the unknown minimum distance of some QR codes.
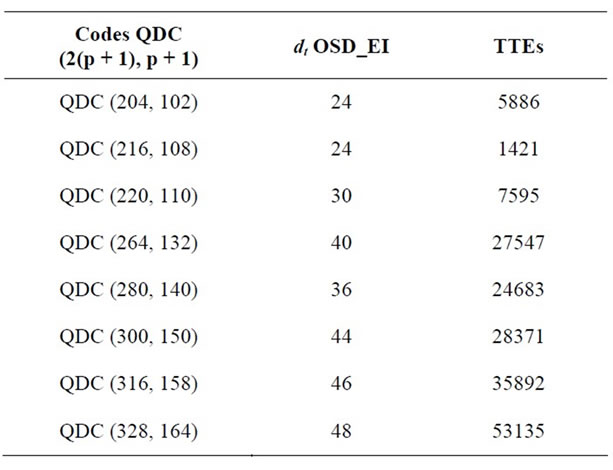
Table 16. Tight bound of the unknown minimum distance of some QDC codes.
5. Conclusion and Perspectives
In this paper we have used genetic algorithms to find a good estimate of minimum distance for BCH, DCC, and QR codes. The implementation of proposed genetic algorithms shows that they are more efficient comparing to competitor genetic algorithm developed by Wallis.
For the same goal, we have proposed the Multiple Impulse Method based on Soft-In OSD decoding algorithm by generalization of the method proposed initially by Berrou et al. The MIM technique is highly performing as a good tool for computing the minimum distance of linear codes, especially for a large code where the length is so long. In the perspectives of this work, we have to apply these powerful tools to construct good linear block codes, and to test the effect of other Soft-In decoders in terms of complexity and performances.
REFERENCES
- H. Chen, N. S. Flann and D. W. Watson, “Parallel Genetic Simulated Annealing: A Massively Parallel SIMD Algorithm,” IEEE Transactions on Parallel and Distributed Systems, Vol. 9, No. 2, 1998, pp. 126-136. doi:10.1109/71.663870
- C. Cotta, E. Alba and J. M. Troya, “Utilising Dynastically Optimal Forma Recombination in Hybrid Genetic Algorithms,” In: A. Eiben, T. BÄack, M. Schoenauer and H. Schwefel, Eds., Parallel Problem Solving from Nature, Springer-Verlag, Berlin, 1998, pp. 305-314.
- J. M. Daida, S. J. Ross and B. C. Hannan, “Biological Symbiosis as a Metaphor for Computational Hybridization,” In: L. Eshelman, Ed., Proceedings of the 6th International Conference on Genetic Algorithms, Pittsburgh, 15-19 July 1995, pp. 328-335.
- K. Dontas and K. De Jong, “Discovery of Maximal Distance Codes Using Genetic Algorithms,” Proceedings of the 2nd International IEEE Conference on Tools for Artificial Intelligence, IEEE Computer Society Press, Los Alamitos, 1990, pp. 905-811.
- M. Askali, S. Nouh and M. Belkasmi, “An Efficient Method to Find the Minimum Distance of Linear Block Codes,” IEEE International Conference on Multimedia Computing and Systems Proceeding, Tangier, 10-12 May 2012, pp. 185-188.
- D. Coppersmith and G. Seroussi, “On the Minimum Distance of Some Quadratic Residue Codes,” IEEE Transactions on Information Theory, Vol. 30, No. 2, 1984, pp. 407-411. doi:10.1109/TIT.1984.1056861
- N. Boston, “The Minimum Distance of the [137, 69] Quadratic Residue Code,” IEEE Transactions on Information Theory, Vol. 45, No. 1, 1999, p. 282. doi:10.1109/18.746813
- D. Kuhlmann, “The Minimum Distance of the [83, 42] Quadratic Residue Code,” IEEE Transactions on Information Theory, Vol. 45, No. 1, 1999, p. 282. doi:10.1109/18.746814
- Markus Grassl, “On the Minimum Distance of Some Quadratic Residue Codes,” Proceedings IEEE International Symposium on Information Theory, Sorrento, 25-30 June 2000.
- W.-K. Su, P.-Y. Shih, T.-C. Lin and T.-K. Truong, “On the Minimum Weights of Binary Extended Quadratic Residue Codes,” Proceedings of the 11th International Conference on Advanced Communication Technology, Vol. 3, IEEE Press, Piscataway, 2009.
- A. Azouaoui, M. Askali and M. Belkasmi, “A Genetic Algorithm to Search of Good Double-Circulant Codes,” IEEE International Conference on Multimedia Computing and Systems Proceeding, Ouarzazate, 7-9 April 2011, pp. 829-833.
- J. Wallis and K. Houghten, “A Comparative Study of Search Techniques Applied to the Minumum Distance of BCH Codes,” Conference on Artificial Intelligence and Soft Computing, Banff, 17-19 July 2002.
- S. Nouh and M. Belkasmi, “Genetic Algorithms for Finding the Weight Enumerator of Binary Linear Block Codes,” International Journal of Applied Research on Information Technology and Computing, Vol. 2, No. 3, 2011, pp. 557-568.
- R. Garello, P. Pierleoni and S. Benedetto, “Computing the Free Distance of Turbo Codes and Serially Concatenated Codes With Interleavers: Algorithms and Applications,” IEEE Journal on Selected Areas in Communications, Vol. 19, No. 5, 2001, pp. 800-812. doi:10.1109/49.924864
- C. Berrou, S. Vaton, M. Jezequel and C. Douillard, “Computing the Minimum Distance of Linear Codes by the Error Impulse Method,” Proceedings of IEEE Globecom, Taipei, 17-21 November 2002, pp. 10-14.
- R. Garello and A. Vila, “The All-Zero Iterative Decoding Algorithm for Turbo Code Minimum Distance Computation,” IEEE International Conference on Communications, Paris, 20-24 June 2004, pp. 361-364.
- S. Crozier, P. Guinand and A. Hunt, “Computing the Minimum Distance of Turbo-Codes Using Iterative Decoding Techniques,” Proceedings of 22nd Biennial Symposium on Communications, Kingston, Ontario, 31 May-3 June 2004, pp. 306-308.
- P. Praveenkumar, R. Amirtharajan, K. Thenmozhi and J. B. B. Rayappan, “Regulated OFDM-Role of ECC and ANN: A Review,” Journal of Applied Sciences, Vol. 12, No. 4, 2012, pp. 301-314. doi:10.3923/jas.2012.301.314
- R. Sujan, et al., “Adaptive ‘SOFT’ Sliding Block Decoding of Convolutional Code Using the Artificial Neural Net-Work,” Transactions on Emerging Telecommunications Technologies, Vol. 23, No. 7, 2012, pp. 672-677. doi:10.1002/ett.2523
- A. Azouaoui, M. Belkasmi and A. Farchane, “Efficient Dual Domain Decoding of Linear Block Codes Using Genetic Algorithms,” Journal of Electrical and Computer Engineering, Vol. 2012, 2012, Article ID: 503834. doi:10.1155/2012/503834
- K. Dontas and K. Dejong, “Discovery of Maximal Distance Codes Using Genetic Algorithms,” Proceedings of the 2nd International IEEE Conference on Tools for Artificial Intelligence, Herndon, 6-9 November 1990.
- D. Coley, “An Introduction to Genetic Algorithms for Scientists and Engineers,” World Scientific, Singapore City, 1999.
- X. Y. Hu, M. P. C. Fossorier and E. Eleftheriou, “On the Computation of the Minimum Distance of Low-Density Parity-Check Codes,” IEEE International Conference on Communications, Paris, 20-24 June 2004, pp. 767-771.
- R. Garello and A. Vila, “The All-Zero Iterative Decoding Algorithm for Turbo Code Minimum Distance Computation,” IEEE International Conference on Communications, Paris, 20-24 June 2004, pp. 361-364.
- M. Zhang and F. Ma, “Simulated Annealing Approach to the Minimum Distance of Error-Correcting Codes,” International Journal of Electronics, Vol. 76, No. 3, 1994, pp. 377-384.
- C. Tjhai, M. Tomlinson, R. Horan, M. Ahmed and M. Ambroze, “Some Results on the Weight Distributions of the Binary Double Circulant Codes Based on Primes,” Proceedings of 10th IEEE International Conference on Communication Systems, Singapore City, 30 October-1 November 2006.
- M. Grassl, IAKS, “Fakultät für Informatik,” Universität Karlsruhe, Karlsruhe, 2006.
- F. J. McWilliams and N. J. A. Saloane, “The Theory of Error-Correcting Codes,” North Holland, Amsterdam, 1977.
- V. Pless, et al., “Handbook of Coding Theory,” North Holland, Amsterdam, 1998.
- I. Krasikov and S. Litsyn, “An Improved Upper Bound on the Minimum Distance of Doubly-Even Self-Dual Codes,” IEEE-IT, Vol. 46, No. 1, 2000, pp. 274-278. doi:10.1109/18.817527

