Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 1 (2012) , Article ID: 16691 , 6 pages DOI:10.4236/ijcns.2012.51008
Secure Cooperative Spectrum Sensing Based on the Distance between Bodies of Evidence
1Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, Hefei, China
2Key Laboratory of Wireless Sensor Network & Communication, Shanghai Institute of Microsystem and Information Technolgy, Chinese Academy of Sciences, Shanghai, China
Email: ricky198324@yahoo.com.cn
Received September 21, 2011; revised November 6, 2011; accepted November 29, 2011
Keywords: Cognitive Radio; Spectrum Sensing; Multiple Thresholds; Energy Detection; Evidence Theory
ABSTRACT
In cognitive radio (CR) networks, unlicensed secondary users need to conduct spectrum sensing to gain access to a licensed spectrum band. And cooperation among CR users will solve the problems caused by multipath fading and shadowing. In this paper, we propose a multi-threshold method at local nodes to cope with noises of great uncertainty. Functions of distance between bodies of evidence are used at fusion centre to make synthetic judgment. To guarantee security which is an essential component for basic network functions, we will take selfish nodes into account which try to occupy channels exclusively. The proposed technique has shown better performance than conventional algorithms without increase the system overhead.
1. Introduction
Cognitive radio is able to fix concurrent problems of scarce spectrum resources and low utilization rate. As an indispensable part of cognitive radio, spectrum sensing can be applied to search for spectrum “space holes” and determine whether to make use of the frequency range, making itself the mostly studied section at present.
Spectrum sensing technologies can be sorted into single user and cooperative spectrum sensing [1]. When the primary user’s information is unknown, utilizing cooperative sensing technologies of multi-CR users exceeds single node algorithm [2] in terms of energy consumption and accuracy. Based on different ways of fusing sensing knowledge, regular fusion algorithms are usually divided into two methods consisting of hard information-combining (HIC) [3] and soft information-combining (SIC) [4]. HIC has relatively smaller communication flow. SIC includes methods based on likelihood ratio detection and linearity. Besides, there are two other special fusion algorithms, one of which relies on relaying protocol and is suited to distributed systems, while the other of which relies on cluster tree[5], which actually is classified as hybrid fusion algorithm. MAC layer detection algorithm focuses on multi-channels and detection time [6]. The spectrum security with regards to malicious nodes gradually becomes the centre of attention [7].
With low SNR and interfering energy of relatively great uncertainty [8], most of the sensing methods cannot lead to correct results. Once every sensing node is in a disparate noise environment, the performance of HIC will be unstable and the capabilities of SIC will also be sharply decreased. The Dempster-Shafer theory [9] of evidence has been proposed for decision making [10] [11]. However, the existing conflict between various CR users is not managed properly by the conventional combination rules [12]. Considering the relevance between CR users, the article will propose an adaptive multithreshold sensing method based on the distance between bodies of evidence on condition that flow load and algorithm complexity are not excessively augmented. The proposed sensing method achieves better performance in terms of such indexes as probability of false alarm and probability of missdetection.
2. System Description
Assuming there is a sensing network consisting of a fusion centre and N sensing nodes in the complex electromagnetic environment, as is shown in Figure 1.
Sensing nodes receive the noises, interferences and information from primary user simultaneously. Each one reflects as to its own surroundings, and then sends results to fusion centre which makes the final decision after receiving judgment results from all sensing nodes: primary user exists (H1) or primary user does not exist (H0):
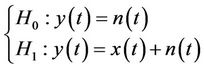 (1)
(1)

Figure 1. System model.
where y(t) denotes mixed signal, x(t) represents received signal from primary user, and n(t) represents received noise.
For local nodes, energy detection is a simple and efficient method. It accumulates energy in a certain range of frequency. When the energy exceeds a certain threshold value VT, it can be concluded that signal from primary user exists. After nyquist sampling, received signal energy can be expressed as:
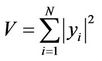 (2)
(2)
The signal with duration of T and bandwidth of W can be represented by N sampling points, while N = 2TW is two times product of duration and band width.
If output sampling points are approximately regarded as independent gaussian variables, output energy meets chi square distribution. On the condition of H0 and H1, output statistics are subject to central and non-central chi square distribution with freedom degree of N respectively. When N stands at a certain large value, detection statistics can approximately be regarded in accordance with gaussian distribution [13]:
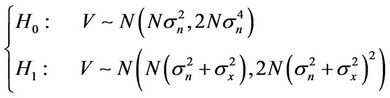 (3)
(3)
where 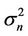 represents noise variance,
represents noise variance, 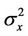 represents signal average power.
represents signal average power.
3.1. New Spectrum Sensing Methods
3.1. Multi-Threshold Detection Methods of Local Nodes
Noise uncertainty will lead to energy fluctuation. When the fluctuation goes up to a certain level, just a threshold value would not be enough to judge primary users accurately, since regular fluctuation can also lead to excessive uncertainty around the threshold. The article will adopt an adaptive multi-threshold detection method at local nodes to adjust to different SNR.
When the SNR is relatively small, if the noise fluctuation during a detection time appears to be large, it will raise probability of false-alarm or probability of missdetection:
 or
or 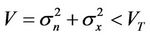 (4)
(4)
Thus, this algorithm enables every CR user to utilize energy detection methods of two thresholds (TH2) or four thresholds (TH4) that corresponds to relatively large or small SNR respectively. The two thresholds of the former one are named as T1 and T2 and the detected energy is divided into three ranges, while the four thresholds of the later one are named as Tl, Tn2, Tn1 and Th and the detected energy is divided into five ranges. The eight ranges are just demonstrated by three bits value, as is shown in Figure 2.
In four-threshold detection method of low SNR, the credibility of energy range 001 and 011 is relatively higher than that of the other three. 001 tends to represent that primary users do not exist while 011 represents the existence of primary users. When the SNR is high, two threshold detection methods should be used. In this situation, 101 and 111 have higher credibility than 110.
Before putting nodes into service, they need to go through an establishing stage when to get familiar with noises in the surroundings based on which the SNR can be determined, and then the threshold mode would be chosen to use. During the working process, the threshold mode can be switched if the SNR changes or sensing performance turns to be undesirable.
CR users are allowed to measure the noise energy received in the establishing stage when primary user does not send signals. The total measuring time is set as nT which can be divided into n stages, with the time for each stage set as T. Thus, peaks and valley values for n stages can be obtained. Average these n groups of data and multiply the average number by necessary coefficients so that Tl and Th can be approximately obtained. Through multiplying all the measured values by their corresponding coefficients, such as 0.9 and 1.1, we can get Tn2, T2 and Tnl, T1.
After the fusion centre receives N groups of binary number ri from CR users, the following evidence theory will be used to decide: R1 primary user exists, R0 it does not exist.
3.2. Evidence Theory Determination of Fusion Centre
The information delivered from different CR users might
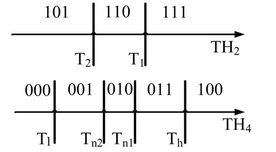
Figure 2. Multiple thresholds based energy detection.
be diverse but undoubtedly related. The article will adopt the functions of distance between two bodies of evidence [14] in evidence theory, and use parameters like the similarity of information transferred among nodes to judge synthetically.
In view of basic belief assignment , m(A) represents the credibility level evidences have in event A. A few basic belief assignments are organized into a belief function to make all-rounded judgment on events. mi represents the basic belief assignment of the ith user, and A, B, C represent three focal elements respectively; therefore, mi(A), mi(B) and mi(C) represent the credibility the ith user has in the existence of primary user, non-existence of primary user and uncertainty. Each of the eight conditions for energy detection corresponds to one probability combination respectively, and these data are stored in fusion centre from the start. In view of the analysis of Equation (3), take the following energy range 010 as example to obtain belief assignment with q-function. Likewise, other seven conditions can be deduced:
, m(A) represents the credibility level evidences have in event A. A few basic belief assignments are organized into a belief function to make all-rounded judgment on events. mi represents the basic belief assignment of the ith user, and A, B, C represent three focal elements respectively; therefore, mi(A), mi(B) and mi(C) represent the credibility the ith user has in the existence of primary user, non-existence of primary user and uncertainty. Each of the eight conditions for energy detection corresponds to one probability combination respectively, and these data are stored in fusion centre from the start. In view of the analysis of Equation (3), take the following energy range 010 as example to obtain belief assignment with q-function. Likewise, other seven conditions can be deduced:
 (5)
(5)
The distance between two bodies of evidence for the ith and jth nodes is:
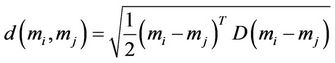 (6)
(6)
where D is a matrix of ,
,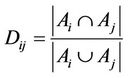
 . Thusthe specific computing method of the distance between two bodies of evidence is as follows:
. Thusthe specific computing method of the distance between two bodies of evidence is as follows:
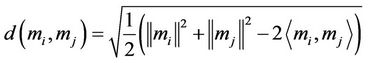 (7)
(7)
where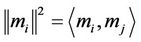 ,
, 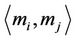 is the inner product of mi and mj.
is the inner product of mi and mj.
Then, the similarity between two nodes can be achieved with the distance between two bodies of evidence:
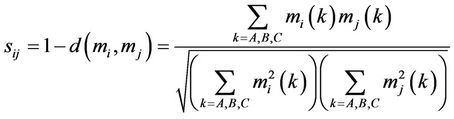 (8)
(8)
sij=sji and sii=1 can be easily drawn. All sij can be indicated in one matrix to obtain the support of wholly sensing network to node CRi
 (9)
(9)
The bigger the value of Sup(mi), the more supported the node CRi, and the more the fusion centre relying on it. All Sup(mi)s need to be normalized to get the weight of nodes when combining:
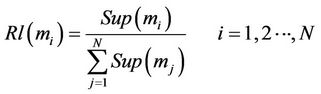 (10)
(10)
The probability distribution after combination can be achieved through Equation (5) and (10):
 (11)
(11)
When m(A)/m(B) > 1, the probability of primary user’s existence is relatively higher; Or according to the objective probability of false alarm and probability of missdetection, a certain proportion value p should be set up, and then when m(A)/m(B) > p, primary user exists.
CRi in Figure 1 might be a selfish node to occupy channels exclusively to claim the existence of primary user. In this algorithm, selfish nodes would try to send the message of “011” or “111”. Thus, common work of primary user would be dramatically influenced, and the sensing abilities of other nodes would be seriously weakened. The safety coefficient sci will be used to avoid such a phenomenon as follows:
if 

else if
 ,
,
 (12)
(12)
New weight is drawn through Formula (10):
 (13)
(13)
This enables the whole system to identify selfish nodes to lower adverse influences to the greatest extent. A certain test result can also be set up, so when the safety coefficient is less, fusion centre would ditch the information of the relevant node.
4. Simulation Results
This section will test the performance of the algorithm (SCS) through simulation. To make the experimental results more universal, relatively small product of duration and bandwidth TW = 5 is chosen. Primary user sends BPSK modulating signal the existence probability of which is 50%, assuming channel noises are gaussian white noise.
Comparison algorithms select the classical algorithms of “OR” and “AND” that all belong to HIC methods. In the algorithm of “OR”, as long as one of the sensing nodes detects primary user, it would be regarded as exists. In the algorithm of “AND”, only if all sensing nodes detect primary user, can it be regarded as exists.
As in Figures 3 and 4, the SNR is set up as 1dB and there are 3 and 6 sensing users respectively, two technical indexes including probability of false alarm and probability of missdetection are utilized. From the comparison with two classical algorithms, the algorithm in the article is with better performance and from two pictures lower probability of missdetections can all be gained under the same probability of false-alarm. When the number of CR users raises from 3 to 6, the three algorithms’ curves all move downwards but the capabilities of this algorithm increase more obviously.
Taken the complex physical background into consideration, every CR user might be in an environment with distinct SNR. In Figure 5, assuming there are five nodes, the SNR are –3, –1, 0, 1 and 3 dB respectively. It is easily seen that due to the existence of nodes with high SNR, the algorithm of “OR” is better than “AND”, but in comparison, the algorithm in the article is still able to achieve better performance.
Figure 6 plays the role to investigate safety coefficient, in which ten users are involved and comparisons are made with 0 ~ 5 selfish nodes. The same local thresholds are used and the probability of missdetection turns to be less than 10%. The results demonstrate that when the number of selfish nodes surpasses two, the safety coefficient still guarantees the probability of false alarm to
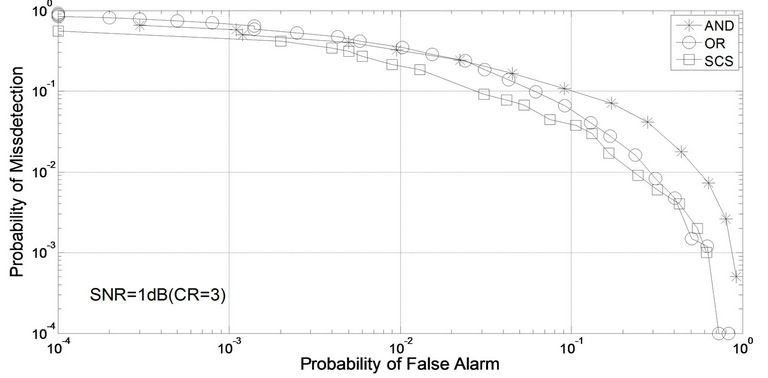
Figure 3. Complementary ROC curves (CR = 3, SNR = 1 dB).
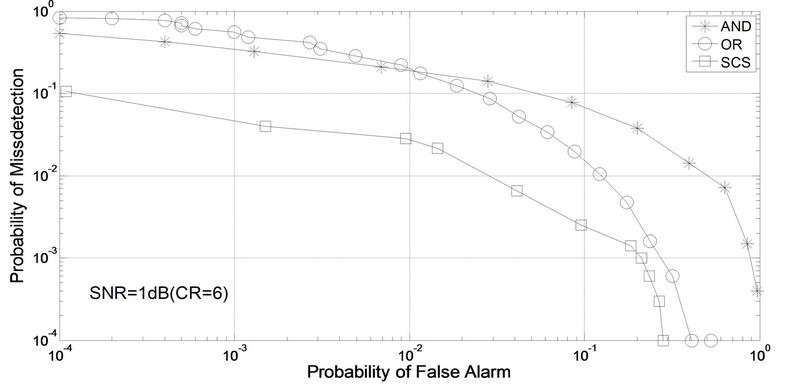
Figure 4. Complementary ROC curves (CR = 6, SNR = 1 dB).
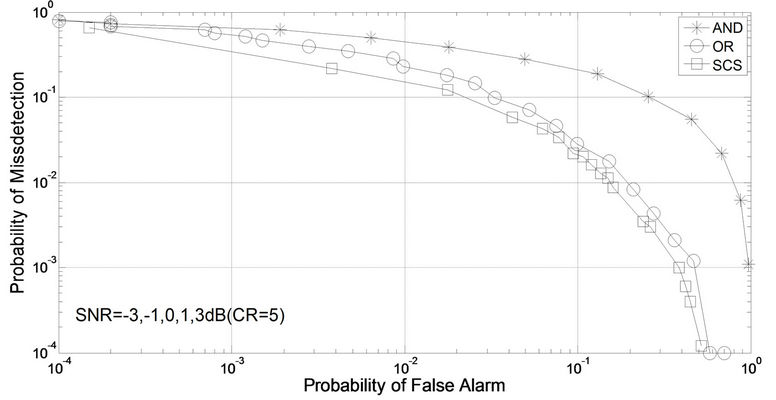
Figure 5. Complementary ROC curves (CR = 5, SNR = –3 ~ 3 dB).

Figure 6. Performance of sensing with selfish nodes.
remain at the quite low level.
5. Conclusion
We have proposed a secure spectrum sensing method based on functions of distance between two bodies of evidence. The simulation results have shown that the proposed sensing technique achieves good performance on condition that no excessive communication flow is added. With the growth of CR users, the probability of detection will also be enhanced. When all CR users are with disparate SNR, primary user can still be precisely detected. The proposition of safety coefficient also gives the system the capability to deal with the assault of several selfish nodes to improve the reliability. However, the study also indicates that when there are not so many nodes and SNR is relatively low, probability of false alarm will not be very high. We will discuss this issue in the future.
6. Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 61071168) and the 211 Project of Anhui University.
REFERENCES
- T. Yucek and H. Aralan, “A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications,” IEEE Communications Surveys & Tutorials, Vol. 11, No. 1, 2009, pp. 116-130. doi:10.1109/SURV.2009.090109
- S. Hussain and X. Femando, “Spectrum Sensing in Cognitive Radio Networks: Up-to-Date Techniques and Future Challenges,” IEEE International Conference on Science and Technology for Humanity, Toronto, 26-27 September 2009, pp. 736-741.
- N. Nguyen-Thanh and I. Koo, “Log-likehood Ratio Optimal Quantizer for Cooperative Spectrum Sensing in Cognitive Radio,” IEEE Communications Society, Vol. 15, No. 2, 2011, pp. 317-319.
- Z. Quan, S. G. Cui and A. H. Sayed, “Optimal Linear Cooperation for Spectrum Sensing in Cognitive Radio Networks,” Selected Topics in Signal Processing, Vol. 2, No. 1, 2008, pp. 28-40. doi:10.1109/JSTSP.2007.914882
- C. M. Qi, J. Wang and S. Q. Li, “Weighted-Clustering Cooperative Spectrum Sensing in Cognitive Radio Context,” WRI International Conference on Communications and Mobile Computing, Yunnan, 6-8 January 2009, pp. 102-106. doi:10.1109/CMC.2009.303
- X. Y. Wang, A. Wong and P. H. Ho, “Extended Knowledge-Based Reasoning Approach to Spectrum Sensing for Cognitive Radio,” IEEE Mobile Computing, Vol. 9, No. 4, 2010, pp. 465-478. doi:10.1109/TMC.2009.148
- R. L. Chen, J. M. Park and K. Bian, “Robust Distributed Spectrum Sensing in Cognitive Radio Networks,” The 27th Conference on Computer Communication, Phoenix, 13-18 April 2008, pp. 1876-1884.
- M. Z. Win, P. C. Pinto and L. A. Shepp, “A Mathematical Theory of Network interference and Its Applications,” Proceedings of the IEEE, Vol. 97, No. 2, 2009, pp. 205-230. doi:10.1109/JPROC.2008.2008764
- G. Shafer, “A Mathematical Theory of Evidence,” Princeton University Press, Princeton, 1976.
- N. Nguyen-Thanh and I. Koo, “Evidence-Theory-Based Cooperative Spectrum Sensing with Efficient Quantization Method in Cognitive Radio,” Vehicular Technology, Vol. 60, No. 1, 2011, pp. 185-195. doi:10.1109/TVT.2010.2086501
- Q. H. Peng, K. Zeng, J. Wang and S. Q. Li, “A Distributed Spectrum Sensing Scheme Based on Credibility and Evidence Theory in Cognitive Radio Context,” IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications, Helsinki, 11-14 September 2006, pp. 1-5.
- E. Lefevre, O. Colot, P. Vannoorenberghe and D. de Brucq, “A Generic Framework for Resolving the Conflict in the Combination of Belief Structures,” Proceedings of the Third International Conference on Information Fusion, Paris, Vol. 1, 10-13 July 2000, pp. 11-18.
- H. Urkowitz, “Energy Detection of Unknown Deterministic Signal,” Proceedings of the IEEE, Vol. 55, No. 4, 1967, pp. 523-531. doi:10.1109/PROC.1967.5573
- A. Jousselme, D. Grenier and E. Bosse, “A New Distance between Two Bodies of Evidence,” Information Fusion, Vol. 2, No. 2, 2001, pp. 91-101. doi:10.1016/S1566-2535(01)00026-4

