Journal of Water Resource and Protection
Vol.6 No.4(2014), Article ID:44264,25 pages DOI:10.4236/jwarp.2014.64032
Geostatistical Methods for Lithological Aquifer Characterization and Groundwater Flow Modeling of the Catania Plain Quaternary Aquifer (Italy)
Enrico Guastaldi1, Andrea Carloni1, Giovanna Pappalardo2, Jacopo Nevini3
1CGT Center for GeoTechnologies, University of Siena, Arezzo, Italy
2Biological, Geological, and Environmental Sciences Department, Section of Earth Sciences, University of Catania, Italy
3Hydrodrilling International S.p.A., Ravenna, Italy
Email: guastaldi@unisi.it, an.carloni@libero.it, pappalar@unict.it, jacoponevini@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 January 2014; revised 5 February 2014; accepted 3 March 2014
ABSTRACT
Sedimentary heterogeneity conditions of Catania Plain quaternary aquifer (CPQA), the wider alluvial multi-aquifer system of Sicily, were rebuilt to simulate and quantify groundwater flow. Transition probabilities based on a Markov Chain (MC) and Sequential Indicator Simulation (SIS) are the structure-imitating simulators utilized for generating stochastic distributions of hydraulic conductivity fields of CPQA, basing on borehole data: plausible equiprobable solutions of the complex geological structure of the CPQA were simulated. This study highlights that the choice of geostatistical simulation method plays a fundamental role in predictive scenarios for groundwater resources managing of CPQA. Indeed, simulated characteristics of the sedimentary heterogeneity constituted the basis of finite difference models for simulating the groundwater flow of CPQA. In heterogeneous systems such as CPQA, SIS may be inadequate for reproducing the macrostructures. Instead, MC adequately reproduced spatial connection of lithofacies, representing a more realistic solution dealing to the proposed geological model of CPQA. MC and SIS models were utilized to both assess the uncertainty of the generated hydraulic conductivity fields of CPQA and predictions about its behavior under normal stress conditions induced by urbanization. The calibration of CPQA groundwater flow models based on MC and SIS simulations allowed to achieve a realistic feedback about the quality of the geostatistical reconstructions of the geological heterogeneity field.
Keywords:Alluvial Aquifer; Lithological Simulation; Geostatistics; Numerical Modeling; Sicily

1. Introduction
The Catania Plain Quaternary Aquifer (CPQA) is the wider alluvial multi-aquifer system of Sicily, Italy (Figure 1). The system is a 428 km2 plain a few kilometers to the South of Mt. Etna, where the town of Catania, its international airport and industrial area, other highly populated villages and specialized agriculture are located. The urbanization of this area in the last decades induced an increased water demand for several activities (drinking water and domestic, agricultural and industrial uses). Water use was not efficiently planned and resulted in the overexploitation of the groundwater, which led to seawater intrusion and aquifers salinization as a result of the concomitant negative effects induced by agriculture and industrial plants [1] [2] .
The aim of this work is to recreate the heterogeneity conditions of depositional systems of the CPQA sedimentary complex by means of stochastic simulations to both simulate and quantify the aquifer groundwater flow. The CPQA consists of geological units that are formed by heterogeneous assemblages from highly to lowly permeable lithofacies, which are generally characterized by large contrasts of hydraulic conductivity. The lithological and spatial heterogeneity at the hydrofacies scale of the alluvial sediments that constitute the CPQA (clay, clay and sand, fine sand, coarse sand, sand and gravel, gravel), as well as other sedimentary deposits studied by several authors, significantly affects groundwater flow, transport and groundwater-surface interactions due to the high variability of the hydraulic conductivity values [3] -[9] . Thus, the uncertainty accompanying the qualitative-quantitative description of lithofacies tends to preclude the possibility for deterministic modeling of subsurface heterogeneity.
A fundamental goal of this work is to recreate the heterogeneity of by means of spatial statistical methods. In general methods to characterize geological heterogeneity can be grouped into three macro sets: 1) structure-imitating methods, which seek to model the subsurface geometry respecting the relationships among geological strata and layers; 2) process-imitating methods, which seek to build the processes that generated the observable layer thicknesses; and 3) descriptive methods, which synthesize a more complex hydrogeological conceptual model by analyzing each lithofacies only utilizing the collected data [10] .
The structure-imitating method was utilized in this study although random field generators could yield a large number of different equiprobable solutions that not always deal with the geological conceptual model. Geostatistical interpolators (spatial statistical methods) could be subdivided on the basis of assumptions about the initial distribution of the studied variables as either Gaussian or non-Gaussian methods. Several authors compared Gaussian and non-Gaussian methods performance, either in real case studies or simplifying the analysis by means of theoretical fields: for instance [11] compare sequential Gaussian simulation and transition probability indicator simulation (or Transition probabilities based on a Markov Chain, hereafter called MC); [12] compare Gaussian and multi-Gaussian simulations; [13] generate permeability distributions by means of Sequential Indicator Simulations (hereafter called SIS), Gaussian/Fractal Simulations and Truncated Gaussian Simulations; [14] compare MC, SIS and Multiple Point Simulation. They showed that all methods lead to significant differences in spatial distributions of simulated lithologies. This work represents not just another comparison between well-known simulation techniques, but, after a new detailed geological conceptual model of CPQA, it assesses also the performances of stochastic heterogeneity reconstructions of a real sedimentary system by means a numerical model, to be provided to the local Authorities for the shrewd management of CPQA groundwater resources.
MC and SIS methods were here utilized to simulate lithofacies heterogeneities in CPQA, the results were statistically post-processed. These methods are well known and widely applicable. Other methods, like for instance Multiple Points Simulation, could have been applied, however the selected methods, here were applied to an important real case, then their results validated with several groundwater flow models and calibrations. A MC provides a stochastic model for spatial variability that is theoretically robust, easily interpretable, mathematically compact, and conceptually simple for quantitative analysis, representing spatial relationships among categorical variables, such as lithological or geological units [15] -[17] . In fact, MC models can consider interclass relationships by means of transition probabilities, even by conditional simulation models [18] -[21] . The interpretation of probabilities in a MC occurs through a transition probabilities matrix, which is derived from the Bayesian concept of conditional probability. Stochastic conditional simulations of facies data coming from both analyzing geognostic logs and interpreting geological conceptual model were performed by means of the T-PROGS package (Transition PRObability Geostatistical Software [15] ), through the calculation of vertical transition probability plots, or transiogram. Following [22] a transiogram is a diagram of 1-D Markov transition probabilities measuring the spatial correlations versus the distance (lag), represented as by the following two-point conditional probability function (Equation (1)):
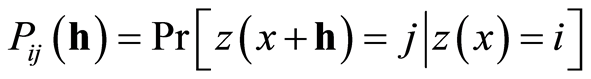 (1)
(1)
where pij(h) is the transition probability of a second-order stationary random variable z from states i to j over a lag distance h; pij(h) of Equation(1) depends on lags (similarly to variograms). Transiograms are organized in transition probability matrix, which each diagonal cell represents the experimental auto-correlation of any individual class (data from same facies), while the other cells are occupied by cross-correlations that quantify the relationships between couples of classes (two different facies correlated on the distance). Experimental transiograms are subjected to mathematical model fitting procedure as well as experimental variograms, and they constitute the basis of MC simulation.
The SIS method [23] -[27] is the other stochastic approach utilized to simulate the geological categorical data. The presence or absence of a particular category is translated into a new data set consisting of either 1 where the thesis is confirmed (the indicator) or 0 elsewhere. The relationships between these two types of values for each threshold, or, in this case, for each present lithofacies, are quantified by experimental variograms. In this sense, each category is studied independently to the others [23] . According to [24] , experimental semi-variogram is defined as expressed by the following Equation (2):
 (2)
(2)
where Z(xi) is the i-th sample value of the regionalized variable z sampled at xi location, and N(h) is the number of sample pairs participating to the calculation of semi-variogram γ(h) for each lag distance h.
The quasi-casualness of lithology distribution in an alluvial depositional system does not allow understanding the way a facies transition appears in a single location (along a vertical drilling hole). For this reason, geostatistical (stochastic) methods were utilized in this study for simulating the geological conditions affecting the flow phenomenon in the aquifer. These geostatistical realizations were the basis of the further stochastic groundwater flow simulations on a three-dimensional multilayer grid by means of the finite difference MODFLOW-2000 code [28] . The numerical model simulates flow through the subsurface hydraulic system and flowing cause-effect relationships by solving spatial differential equations associated with specific boundary conditions. The partial differential equation governing groundwater flow used in MODFLOW is the following Equation (3):
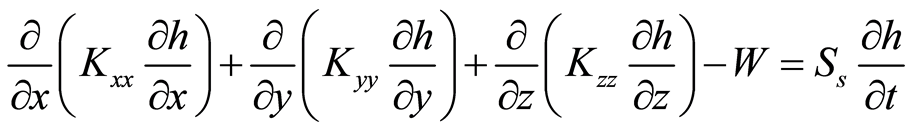 . (3)
. (3)
where Kxx, Kyy and Kzz are the values of hydraulic conductivity along the x, y, and z coordinate axes; h is the potentiometric head; W is a volumetric flux per unit volume representing sources and/or sinks of water, where negative values are extractions, and positive values are injections; Ss is the specific storage of the porous material; t is the time. MODFLOW is the US Geological Survey modular finite-difference flow model, which is a computer code that solves the groundwater flow equation.
The hydraulic head is the unknown variable in the system for simulating groundwater flow in CPQA aquifer, assumed as saturated. Uncertainty of the achieved solutions principally depends on both the quantity of the available data and the hydrogeological conceptual model, secondarily on the requested simplifications for solving the flow equation (see Equation (3)).
Thus, quantitative analysis of the lithology heterogeneity effects on the hydraulic conductivity spatial variability is a fundamental step for numerical flow modeling. In fact, this aspect facilitates the conceptualization of structures that define the preferential groundwater flow paths. Errors in the geological conceptual model framework could lead to simulating scenarios significantly different from one another, especially in alluvial aquifers. One way to encompass this criticality is to verify several plausible scenarios by formulating and applying possible alternative spatial geological models to provide a multi-predictive model. Differences among model forecasts based on the conceptualizetion alternatives are a measure of the model structure’s uncertainty. Therefore, both the model predictions adaptability to geological conceptual model and the reliability of simulating geological heterogeneity (process imitating) will be tested by solving the flow equation (Equation (3)).
2. Study Area
The quaternary aquifer of the Plain of Catania (CPQA) is located between Mt. Etna and the Hyblean Foreland (Plateau) (Figure 1) and represents the portion of the Plio-Quaternary foredeep [29] -[31] that originated from the northern margin of the Hyblean Plateau collapse due to extensional faulting [32] . The geological and geophysical data suggest that the collapse occurred after the Late Pliocene [33] as a result of the progressive migration of the Maghrebian thrust wedge (the Gela Nappe front) toward the foreland [34] . The CPQA is bounded northward by the Terreforti Hills and southward by the S. Demetrio High, which separates CPQA by the coeval Plio-Quaternary sedimentary basin of the Lentini Graben [33] (Figure 1).
The CPQA’s stratigraphy is characterized by four depositional sequences from the Pliocene to now [1] [33] [35] . These sequences are characterized by different depositional settings and differ in location, particle size, and genesis [2] .
The oldest sequence (DS1) is characterized by submarine marly clay of the Lower-Middle Pleistocene [36] -[39] and represents the CPQA’s bedrock (Figure 1 and Figure 2). According to the oil drilling data (boreholes “Catania 012”, “Rizzo 002” and “Rizzo 003” [40] ), the marly clay in the central part of the Catania Plain exceeds 700 m in thickness.
The bottom of this clay has been crossed by submarine basaltic lava-flow deposits [2] . The Sicilian marly clay is folded and faulted [41] . The marly clays are exposed along the northern and western margins of the CPQA, at the base of the Terreforti Hills (Figure 1) [2] .
Upward from DS1 is DS2, which has an unconformity on DS1 and outcrops along the Terreforti Hills. It is made of sandstones and gravel belonging to the middle Pleistocene S. Giorgio Formation ([39] ), which is a coastal shallow-marine sedimentation [42] and fan delta [43] .
The third depositional sequence (DS3), the Mt. Tiritì Formation [2] [39] , consists of gravel with sandy conglomerate intercalations that are weakly cemented. The boundary with the lower S. Giorgio Formation is eteropic. The latter formation represents a middle Pleistocene alluvial-deltaic deposit.
The described sequences (DS1, DS2 and DS3) are marine and fan delta regression quaternary deposits, which partly outcrop, constituting the Terreforti Hills, and are partly under the alluvial Simeto River. The latter is set inside a graben created during the Plio-Quaternary tectonic phase [44] [45] . This graben is filled by the DS2 and DS3 Middle Pleistocene depositional sequences and represents the most productive part of the CPQA; the industrial and commercial districts of the town of Catania are in this area (Figure 1).
The topmost succession of the Plain of Catania is represented by the youngest depositional sequence (DS4, Figures 1 and 2), which is alluvial, created in a period from the Holocene to the present. It fills the Plain of Catania’s quaternary morpho-structural depression, and consist of fine sands, silts and gray muds, with lenticular gravel bodies.
With 133 stratigraphic observations coming from water wells and geognostic drillings, two sections have been realized to highlight the existing relations between the four described depositional sequences. Sections A-A’ and B-B’ (Figure 2) show the tectonic contact between the DS1 Hyblean volcanic formations (HF in Figure 1) and the sedimentary ones (DS2, DS3 and DS4). The southern part of section A-A’ highlighted that DS4’s finest sediments lie directly on the clay basement (DS1), demonstrating that there are no coarse sediments South of the Simeto river. Section B-B’ (Figure 2) shows the aquifer’s longitudinal development, particularly emphasizing how the eastern part of the plain is affected by a thickening of sediments and a subsequent tectonic rise moving coastward, represented by a structural high, due to the collision of the Hyblean Plateau and the Maghrebian thrust front [33] .
The CPQA, because of the vertical and horizontal distribution of the clastic deposits within the stratigraphic succession, exhibits extreme variability in aquifer productivity. The alluvial deposits composed of silty clay, sands and gravel are characterized by discontinuous levels of clayey silts that reduce permeability. The filling quaternary clastic deposits (the San Giorgio and Mt. Tiritì sequences), which consist of sands, gravel and conglomerates, exhibit higher permeability, having lower levels of silty clay, and represent the main aquifer [2] .
The quaternary aquifer system consists of two macro layers, each having distinct hydraulic properties. The upper layer includes silty clay from recent deposits (DS4 in Figure 2) and has a reduced thickness, whereas the
 (a) (b)
(a) (b)
Figure 1. (a) Location of the study area and geological sketch of Eastern Sicily (red lines with triangles: main thrusts. red lines: main faults); (b) Depositional units of the Plain of Catania. Coordinate System: ED50 UTM zone 32 North.
deep layer, consisting of DS3 and DS2 (Figure 2), is more productive and exhibits high hydraulic conductivity. This layer is located inside the Simeto Graben and in the Terreforti Hills. The deep aquifer is under pressure from the overlying aquitard. The top and bottom surfaces of the two aquifers have been reconstructed by combining two interpolations: a linear geostatistical interpolation (ordinary kriging, see, for instance [24] ) and a polynomial regression [46] applied to 123 boreholes for the superficial aquifer and 133 for the deep one. The thicknesses were calculated by utilizing the DEM of the area (spatial resolution of 10 meters). The two aquifer’s portions reach a maximum thickness of 40 m for the sediments inside the superficial aquifer and a maximum of 80 m for the deep one.
Hydrostratigraphic surface reconstruction was carried out using the original borehole data integrated with the geological sections and literature data [1] [33] [47] [48] [49] . The processing produced two surfaces, with some interconnected water volumes identified (Figure 3), given by deposits whose thicknesses vary from East to West and, to a greater extent, from North to South. The deep aquifer in the northern part of the CPQA (Terreforti Hills) becomes phreatic in contact with Etna’s volcanic rocks. The deep aquifer’s greatest thicknesses, estimated at approximately 80 meters, are located in the eastern sector below the industrial area (Figure 1) [1] [2] . This result supports the previous reconstruction of [44] based on geoelectrical investigations.
The superficial aquifer’s piezometric surface is between 5 m a.s.l. to over 50 m a.s.l. in the southeastern part of the basin, whereas the deep aquifer’s reaches a depth of −30 m a.s.l. in the central part of the plain (Figure 4). The groundwater flow path has a W-E direction [1] and coincides with the depocenter axis of the CPQA basin.
The aquifer is partially fed by the water contributions coming from the main rivers’ valleys, the quantification of these outflows is hardly determinable because of the lack of reliable data on superficial outflows and, as a

Figure 2. Geological-interpretative vertical sections of the alluvial deposits of the CPQA, with wells and drilling hole localizations (see Figure 1 for locating of section traces).



Figure 3. Three-dimensional reconstruction of geometry and volumes of alluvial aquifer: high-conductivity deeper aquifer in yellow; low-conductivity upper aquifer in dark green; bedrock (assumed aquiclude) in gray.

Figure 4. Estimation of static potentiometric surface of the CPQA, main groundwater flow paths, and grade of relative permeability of lithologies related to different depositional units.
consequence, the exchange between rivers and aquifers; this aspect justifies the apparent balance deficit against the total volume of withdrawals, which is estimated at approximately 22.5 × 106 m3/year [48] .
The CPQA is connected to more complex structures towards the North and South. In these boundary areas of the CPQA, it was not possible to quantify the groundwater volumes that concern all the hydrogeological structures using the available data. The rainfall data used in the water balance calculation are related to the average annual values regarding the ten closest weather stations available in the studied area [50] . It is important to note that although steepness decreases considerably inside the plain, the effective infiltration is rather scarce because of the superficial fine alluvial deposits, which do not allow infiltration. The hydrological balance estimations show how the aquifer presents a water deficit due to the overexploitation resulting from the withdrawals for irrigation and industrial activity [48] .
3. Materials and Methods
Reconstructions of geological heterogeneity were realized using two different geostatistical approaches for the simulation of categorical variables, i.e. means the lithologies that constitute the CPQA basin.
3.1. Stochastic Reconstruction of Sedimentary Heterogeneities
The spatial statistical methods, either MC or SIS, were considered in this study and tested in terms of reliability. The results of these simulations will be utilized later as the geological basis for the numerical groundwater flow model. In particular, both methods are non-Gaussian simulators and useful for interpolating categorical data such as the lithological composition of drilling holes. The methods were utilized for studying either the spatial variography or facies transition probabilities. Both methods, one covariance model based (SIS) and the other based on transition probabilities (MC), utilize geological information, taking into account eventual spatial anisotropies and transition frequencies among different lithologies. The simulation solutions of these methods respect the frequency distribution of the original data, honor the value at the sampling location, and utilize the hydrostratigraphic cross sections are used to infer the parameters for the horizontal components of the variogram (SIS) and of the transition probabilities (MC).
Stratigraphic data (lithofacies) from geognostic drilling holes were simplified and normalized in terms of hydrogeological units (HGU) for conceptual modeling of the CPQA. This led to subdividing the reservoir into two portions with the aim of achieving two smaller but more homogeneous aquifer volumes according to genetic sedimentation and hydrodynamics properties (Figure 3). Descriptions of the main lithologies analyzed using the available drilling holes are summarized in Table 1. These facies categories, hereafter considered geostatistical categorical variables, are afferent to lithofacies previously described in the study area paragraph.
The spatial distribution of punctual data (drilling holes) is homogeneous in the study area, even if a denser sampling is located in both the central part of the CPQA (Catania’s industrial area) and in the Terreforti Hills, where the phreatic aquifer is intensively exploited (Figure 4).
The depths of the drilling holes generally range from 40 to 60 m deep from the ground surface: the maximum depth reached by wells is greater than 300 m (see Table 1). The measured lithologies did not provide any indication about passing from one lithofacies to another in both aquifer’s portions (Table 2).
Considering the available data for implementing the MC method, the variability of the drilling holes structures, and the depositional history of the CPQA, the discrete lag approach ([15] ) was utilized as a favorable compromise between the complexity of stratigraphy and a time-consuming algorithm, as suggested by other studies [11] [51] [52] . The transition matrices in the simulated volumes of both portion of CPQA aquifer (i.e. two finite states) play the role of Markov kernel process.
Then, the vertical transition probabilities for passing from one state of the variable (i.e., a specific lithofacies) to another were propagated in the horizontal plan (3D MC) by utilizing the lens length-to-thickness ratio (LLR) as a multiplier for horizontal distances, which are equal to 10 times the vertical distances. This choice kept into account the typical alluvial sedimentary geometry according to the Walther law [53] . In fact, transition probabilities showed a sequential unconformity among the found lithologies. Conditional stochastic simulation of the spatial distributions of categorical variables, such as lithological differences found in drilling holes, were performed by calculating 30 three-dimensional equiprobable simulations.
SIS is an indicators geostatistical simulation, a stochastic approach honoring the spatial variability of original data [54] . Several authors (for instance, [14] [55] ) utilized SIS for simulating the sedimentary heterogeneity of alluvial deposits; SIS was performed in Isatis [56] .
This conditional simulation procedure utilized allowed to perform several simulations of a categorical variable honoring all the input data, yielding a simulation of the hydrogeological units (i.e. either HGUs of upper or lower aquifer). In particular, the variation range of input categorical variable was divided into a set of intervals, each one corresponding to a facies [56] . Conversely to a MC, this SIS model is fully 3D in all steps, and it follows the usual procedure of geostatistical analysis of data by variography analysis, even if it does not consider a Gaussian distribution for the studied variable.
Table 1. Main descriptive statistical parameters of lithologies in the CPQA drilling holes.
Table 2. Occurrence of simulated voxels belonging to both portions of the CPQA alluvial aquifer.
3.2. Groundwater Flow Model
The adaptability and reliability of the simulated heterogeneity models by both MC and SIS geostatistical methods were assessed through fundamental equations of flow numerical models in a saturated porous medium, then verified using calibration techniques. The equations describing the continuous groundwater flow movement system were solved using the MODFLOW-2000 numerical code [28] .
3.2.1. Numerical Model Implementation
The calculation domain was a 20 × 17 km rectangular area with the minor side parallel to the coastline. The horizontal plain was regularly discretized by 200 × 200 m cells in 100 columns and 85 rows. The deformed grid was subdivided into 12 layers, discretizing in six layer the upper portion of the aquifer volume, and in other six the lower portion of the reservoir, with the highest hydraulically conductive and a thickness ranging from 1 m to 10 m. The E-W grid orientation reflects the general path of the main groundwater flow direction (modeled area, dashed rectangle in Figure 4), whereas the chosen size of cells considers the extent of the CPQA plain regarding both the heterogeneity of hydrodynamic parameters and the minimum distance between original data. Unique hydraulic conductivity values were assigned to each lithofacies for implementing the model in a steady state according to literature, since both recent and reliable pumping tests are not available (Table 3).
The boundary conditions were specified for solving the flow equation. Precipitation recharge was assigned as imposing a flow in mm/year (Neumann condition, assigned by Recharge Package [60] ).
Three different recharge areas were individuated, the first in the Terreforti Hills in the North, the second occupying the whole plain area, and the last in the limestone-basaltic complex of Mt. Iblei in the southern part of the study area.
The recharge values of the three areas were calculated by comparing geological information, rainfall data from the ten closest stations, and by utilizing the runoff curve number method [61] : three recharge zones were individuated, with recharge values equal to 8, 180, 50 mm/year. The evapotranspiration was attributed to the model using the Evapotranspiration Package [60] . However, only one mean area of evapotranspiration was calculated by the method of [62] , due to the available scarce data of rainfall and temperature.
The influence of the Simeto, Dittaino and Gornalunga Rivers on the groundwater system was simulated by means of the River Package [60] by assuming for river bed sediments an hydraulic conductivity value equal to 10−3 m/s as clear gravel and a thickness of 1 m. River flow levels were inferred from the data of local hydraulic authorities for the period of 1990-2009. The Simeto River had an average riverbed width equal to 30 m, whereas its tributary rivers, the Dittaino and Gornalunga Rivers, were smaller (riverbed size of 10 m). However, the same square cells of 200 m, greater than the main riverbed, were utilized to discretize all riverbeds, accentuating the influence of the three main streams to the aquifer. Nevertheless, a grid refining would have produced a useless greater number of cells, without achieving better simulation results. The Well Package [60] was utilized to simulate the groundwater exploitation through the CPQA wells, mainly located in Catania’s industrial area, close to the coastline, and in the Terreforti Hills. Based on [48] , the estimated volume pumped per year was approximately 22 × 106 m3, half of which was used in the industrial area for productivity purposes and the other half of which was destined for agriculture and drinking purposes.
The hydrogeological model with boundary conditions of the first order (Dirichlet condition) was chosen in order to both minimize the solutions variation due to the effect of the input or output flows from the computational domain, and to reduce the calibration parameters. In this way, during calibration, it was possible to focus mainly on aspects related to various fields of hydraulic conductivity and reconstructed by sensitivity analysis to
Table 3. Lithofacies (HGU) and hydraulic conductivity values according to some authors [57] [58] [59] .
verify how the different numerical parameterizations of hydraulic conductivity may affect the numerical model solutions. A sea coast limit condition was assigned using a constant hydraulic head (Constant Head package [60] ); the same condition applied for incoming groundwater flows from the western part of the study area. Hydraulic heads were assigned on the basis of the monitored piezometric levels interpolated by means ordinary kriging.
Three different groundwater flow models in a steady state were implemented with the same spatial geometrical discretization (hereafter noted as A, B, C).
A simplified hydraulic conductivity field was assumed for Model A that had only two different layers with homogeneous hydraulic conductivity for each HGU, one assigned to the upper recent alluvial sediments and the other to the deeper portion according to the depositional conceptual model. Five different hydraulic conductivity values were assigned to the main lithofacies (HGU) for the B and C models, due to the stratigraphic interpretation of drilling holes and the three-dimensional reconstructions simulated, respectively by a MC and SIS.
3.2.2. Numerical Model Calibrating
Hydraulic conductivity values for each HGU were defined in the calibration step. Then, 5 possible conductivity configurations were chosen, from the minimum, Kmin, with hydraulic conductivity values lower than the literature range of each HGU, up to the maximum, Kmax (Table 4). In particular, calibration of the CPQA groundwater flow numerical model was performed to assess its reliability by means of a trial-and-error approach, starting from values utilized for implementing the model in a steady state (Table 3), then varying K values of some order of magnitude, ranging from 5 × 10−6 - 1 × 10−7 m/s for Silts to 1 × 10−7 - 1 × 10−11 m/s for clays (Table 4).
Uncertainty in the simulating hydraulic heads was evaluated starting from the descriptive statistical parameters of the function of errors between the calculated and observed heads in 75 wells homogeneously distributed in the CPQA (static levels monitored from 2006 to 2008, from [50]). This step was done to minimize the errors function (in terms of maximum, mean and minimum of residuals, standard errors, raw and normalized root mean squared, and correlation coefficient between original data and estimates, Table 5), by considering both the extent of the study domain and the spatial distribution of observation points, along with experimental and systematic errors in the measuring of groundwater levels.
4. Results and Discussion
The results of geostatistical simulations will be discussed by comparing them with the conceptual geological model, and then their performances as a basis for numerical models will be analyzed.
4.1. Analysis of Simulation Results Compared to the Geological Conceptual Model
For the MC method, the theoretical functions were fitted on the experimental data by means of lags equal to 20 m for the upper part of the CPQA’s aquifer and 10 m for the lower one, by inferring the 1-D vertical transition probability matrices of the two volumes (Figure 5). The achieved equiprobable simulations confirmed the field data that only some lithofacies were present in the sedimentary alluvial complex with similar occurrences in both the upper and lower portions of the CPQA (sands and silts, respectively, related to the hydrogeological units (HGUs) 4 and 5, Table 2). The large vertical variability, the approximation due to a LLR assumption, the large variability affecting the transiogram model fitted on experimental data (Figure 5) and the huge lateral lithofacies heterogeneity with regard to the sampling pattern affected the MC simulations results, yielding realizations less comparable to each other in terms of facies spatial distributions.
Theoretically, each realization could simulate the facies heterogeneity, however a post-processing solution was chosen for obtaining reliable results more representative of the sedimentary reality of the alluvial basin of CPQA. In fact, each equiprobable simulation honors both the frequency histogram and the spatial correlation of the original data. The statistical post-processing of simulations allows to assess the data uncertainty, without significant modification of the spatial correlation patterns of original simulation. In particular, each 3D cell (voxel) of reservoir volume contains several simulated lithofacies values: if the same facies value is simulated many times in one voxel, then this facies is probably the most representative of the true unknown facies of this voxel in the discretized CPQA volume.
On this basis each voxel was summarized through mode statistical parameter in order to obtain the grid of the most frequent facies per voxel, but no scale change were performed.
Table 4. Hydraulic conductivity test values assigned to HGUs for calibrating the CPQA numerical model.
Table 5. Descriptive statistical parameters of numerical calibration of 75 data points for A) homogeneous models, B) sedimentary heterogeneities simulated by a MC, and C) sedimentary heterogeneities simulated by SIS..
 (a)
(a) (b)
(b)
Figure 5. Transition probability matrices plots for (a) lower part of the CPQA aquifer and (b) upper part of the CPQA aquifer (dashed line: experimental data; green thick line: transiogram model).
However, even if it’s a statistical parameter statistically robust toward the outliers, the mode of the relatively small but consistent number of equiprobable simulations achieved is a statistical parameter that tended to underestimate the less measured lithofacies, such as silts and clays in the lower aquifer. Table 2 demonstrates that sands and gravels are more abundant in the lower part of aquifer than others lithofacies; however, the upper aquifer contains a large occurrence of finer facies, such as clays.
For the SIS method, the two parts of the CPQA reservoir were considered separate as well. Superficial aquifer data showed a not so evident spatial geometrical anisotropy, with the azimuth of the ellipsoid main axis oriented N70˚. This experimental condition of spatial variability was fitted by means of a three-dimensional variogram model (Figure 6). The variogram model was verified by means of the cross-validation procedure [63] . The statistical results were acceptable (mean of standard errors, MSE, = −0.002, variance of standard errors, VSE, = 0.97) even if the correlation between the single estimated data and the raw data was statistically low (rho = 0.474).
The same procedure was utilized for simulating the lower part of aquifer. In fact, a clear spatial geometrical anisotropy is evident, with the main axis N 65˚ oriented as shown in Figure 7(a). By contrast, in the vertical direction, the experimental variogram showed a smaller scale variability, even if it was lower than the variability for the upper part of aquifer (Figure 7(b)).
This is a direct effect of the different number of data in the two CPQA aquifer’s portions, larger in the deep part than in the superficial one.
Additionally, in this case, the cross-validation procedure provided good scores (MSE = −0.0077, VSE = 0.99) although the correlation coefficient was lower than the previous one (rho = 0.236), due to large spatial heterogeneity. SIS results were post-processed by mode like those for the MC method.
Preliminary evaluations of the geological models of sedimentary heterogeneities were performed to verify the quality of each simulation. The expected sedimentary characteristics (proportions, size, trends) were analyzed by means of a qualitative comparison between geostatistical simulations and the interpretative geological sections of the lithostratigraphic model shown in Figure 2. However, the simulations could not reproduce lithofacies relationships smaller than grid discretization, i.e. lower than 200 × 200 m on the horizontal plain and from 1 to 10 m on the vertical plain.
Moreover, the lower the initial geological knowledge is, the greater the probability of considered wrong assumptions in process imitating would be, then good qualitative coherence is not synonymous with quantitative realism [26] . Consequently, the main characteristics coming from the geological stratigraphic conceptual model, assumed as a reference image, were assessed.
In particular, two features were detected: 1) vertical lithostratigraphic anisotropy related to the depositional genesis of the sedimentary body, with various lithofacies frequency distributions in both the upper alluvial unit (DS4), characterized by a larger occurrence of gravel and sand HGUs, and the lower ones (DS2 and DS3), characterized mainly by clay and silt HGUs; 2) the horizontal asymmetric disposition of sedimentary structures has a major axis elongated in the E-W direction, coherent with the main groundwater flow direction, in the upper hydrostratigraphic unit (DS4) and in the N-S direction in the lower ones (DS2 and DS3).
Concerning to the vertical lithostratigraphic anisotropy, a larger presence of sands than other HGUs in the lower part of the aquifer for both geostatistical models was highlighted, even if the MC simulated this lithofacies more than the SIS did (Table 2). Analyzing the horizontal plain anisotropy of each lithofacies, the MC simulated realizations (Figure 8) with sands and gravels prevailed, with good connections, showing wide continuous structures that were mainly N-S elongated. This condition was mostly evident in the Terreforti Hills out-crops. Clays and silts were simulated in SIS realizations of the upper part of the alluvial reservoir with a high easternwestern anisotropy direction, distinctly lower than those obtained by means of the MC models and with more sands with respect to the geological conceptual model.
Therefore, MC simulations (Figure 8) were more coherent with the reference model, HGUs reproduced vertical lithostratigraphic anisotropy and the asymmetric horizontal one respected the genetic sedimentary pattern. Simulated lithofacies distributions yielded by SIS realizations (Figure 9) were less connected than those achieved by the MC; only in the horizontal plain clay and sand HGUs were organized in spatially continuous structures.
The frequency distributions of the raw data of the DS4 upper unit showed clay (43%) and sand (48%) lithofacies prevalent over gravels and silts, whereas in the lower units (DS2 and DS3), gravels (40%) and sands (42%) were the most prevalent.



Figure 6. Experimental semi-variogram and respective model of HGU #5 (Sand) for upper part of the CPQA aquifer: (a) global view and (b) the vertical direction only.



Figure 7. Experimental semi-variogram and respective model of HGU #5 (Sand) for lower part of the CPQA aquifer: (a) global view; (b) the vertical direction only.
Both the 1 and 5 HGUs simulated by SIS were more abundant than those resulting from the MC (Figure 8, Figure 10(a)). Moreover, the MC modal simulations showed good coherence with the input data (Figure 8, Figure 10(b)).
On the contrary, the SIS model overestimated clays (18%) and gravels (28%) in the lower part of the CPQA aquifer, whereas sand (58%) prevailed over clays (37%) in upper part (Figure 9(b), Figure 10(d)).
Mode post-processing of the equiprobable simulations of the categorical variables determines sensitive shifting with the frequency distribution of the input data. In fact, mode post-processing of a large number of simulations provides a decreasing percentage of low-frequency categories, and the simulated classes with higher fre-

Figure 8. Perspective views of sedimentary heterogeneity result, simulated by a MC, one model column (a) and one model row (b), comparable to vertical section of the geological sedimentary conceptual model shown in Figure 2.
quencies than the raw ones are emphasized.
In fact, the mode is a robust statistical parameter non-affected by outliers: another parameter, i.e., the mean, is advisable, even if it is less consistent than the median. However, both the average and median are meaningless in the statistical analysis of categorical variables. A unique modal representation statistically post-processed from several stochastic equiprobable simplifies the further hydrogeological modeling since tends to increase the simulated portions with the same facies, even if it could introduce errors in hydraulic conductivity modeling. However, we checked the good performances of post-processed simulations of heterogeneity by means of the calibration of groundwater flow model. On the contrary, the non-conformity with the input data distribution does not imply a shifting from reality because it is assumed, but not proved, that the surveyed data could correctly describe the variable in space.
The geological model-based method (MC) highlighted difficulties in transposing the 1D chains to 3D. The simulation method does not allow us to manage the uncertainty in the choice of the ratio between the size of the structures. Such criticality means that the relationship between the proportions of length and thickness of the structures (lens length proportions, LLP) are wrapped and strongly restricts the reconstruction of geological elements at a scale less than that of the same LLP. The field of heterogeneity evaluated by the covariance modelbased method (SIS) instead gives rise to small interconnected structures that, as is the case of the SIS model, give rise to very erratic patterns. This is attributable to the difficulty in modeling the experimental semi-variogram (ESV) for excessive anisotropy of scale between the x, y and z directions. In fact, the model fitted on the three-dimensional indicators ESV comes from 200 m lags in the xy plane, while few tens of centimeters lags in z plane. The calculation is complicated not only by the huge difference in scales between the planes xy and z but also by the use of a deformed grid, which introduces additional problems for spatial analysis.
4.2. Predictive Models Results
A process-imitating approach allowed us to verify the quality of the geostatistical reconstructions by comparing

Figure 9. Perspective views of sedimentary heterogeneity result, simulated by SIS, one model column (a) and one model row (b), comparable to the vertical section of the geological sedimentary conceptual model shown in Figure 2.
various heterogeneity models on the basis of groundwater flow phenomena. Different fields of hydraulic conductivity associated to groundwater flow have significantly influenced the numerical simulations solutions, producing distinct velocity fields with different approximations of the observed hydraulic heads.
The modeling calibration scores of the “A” models (homogeneous) highlighted that the best of five configuration is Kmean (Model A3, in Table 5), with hydraulic conductivity equal to 10−6 m/s in recent alluvial deposits (DS3 and DS4) and 10−3 m/s in deeper aquifer deposits (DS2). These conductivity values led to a correlation coefficient of simulated vs. observed piezometric data (residuals) equal to 0.72, with a normalized mean error of 28% and an absolute mean of residuals of 7.68 m (Figure 11(a)). The unimodal residual distribution shows that the calculated hydraulic heads over-predicted the observed ones. This condition was stressed by means of a less conductive configuration (Model A1), with RMS equal to 40.8%. In Model A3, only a few estimated values fell outside the 95% confidence interval, which is generally considered as one satisfactory solution for modeling. This result ensured a good representation of hydraulic heads on the CPQA’s edges, where groundwater flow model solutions are affected by boundary conditions, whereas hydraulic heads were scarcer in the central part of the plain, where wells were more exploited and both local confining and semi-confining phenomena were present (Figure 13(M1)).
“B” models, simulated by utilizing heterogeneity fields coming from a MC, determined a better approximation of the estimated hydraulic heads based on the observed ones, with the best fitting for Klow (Model B2), a correlation coefficient equal to 0.95, a normalized root mean squared error (NRMS) of 8%, and an absolute mean of residuals slightly greater than 2 m (Table 5).
Both the simulated versus observed heads scatter plot and the function of the residual distributions generally over-predicted the simulated head. The residual distribution of Models B4 showed clear bi-modality; the main population values were on the calibration line, whereas the other less representative values had the highest errors.
This subset of points over-predicted the hydraulic heads in the central part of the CPQA, close to Catania’s

Figure 10. Comparison between facies distribution in the CPQA alluvial reservoir, simulated by a MC (a and b) and SIS (c and d), shown in a horizontal section at −20 m a.s.l. and in both an East-West vertical section (a and c) and a North-South vertical section (b and d).
industrial area, where groundwater is unconfined due to a large clay lens in the upper part of reservoir. This was supported by the uncertain trend of Model B2’s potentiometric surface, due to the high contrast in hydraulic conductivity among gravels, sands and clays in this area. However, this trend was not detected in Model A5, the homogeneous case, which had a smooth water table without large potential contrasts.
For the “C” models, which are characterized by hydraulic conductivity simulated through SIS, Klow (Model C2) provided a good optimization of residuals in the calibration step compared to the K range of Table 5, with a correlation coefficient equal to 0.86, a NRMS of 14.7% and an absolute mean of residuals of 2.8 m. This model showed a sensitive increasing of residuals; the NRMS is almost twice that of the B models. This difficultly in model calibration was due to a lack of spatial continuity of HGUs, especially for both the horizontal plain and the lowly permeable simulated lithofacies (silts and clays). In this sense, the simulated hydraulic heads are largely approximated in the central part of the CPQA, where groundwater is confined (Figure 11(c)). The water table of Model C2 in the south-central part of study area (Figure 13(M3)) exhibited a behavior similar to Model B4, where in the low permeable sectors of the upper unit, the water table is more regular, a characteristic feature of homogeneous models.
Sensitivity analysis of the uncertainty of the model solutions was performed by varying K. The defined variations of hydraulic conductivity inside the imposed range for each HGU in Model A (homogeneous) determined substantial variations in the model solutions up to optimal calibrations, without reducing residuals (Figure 12(a)). K variations inside the reference ranges for both the “B” and “C” models (with heterogeneities) yielded
 (a)
(a)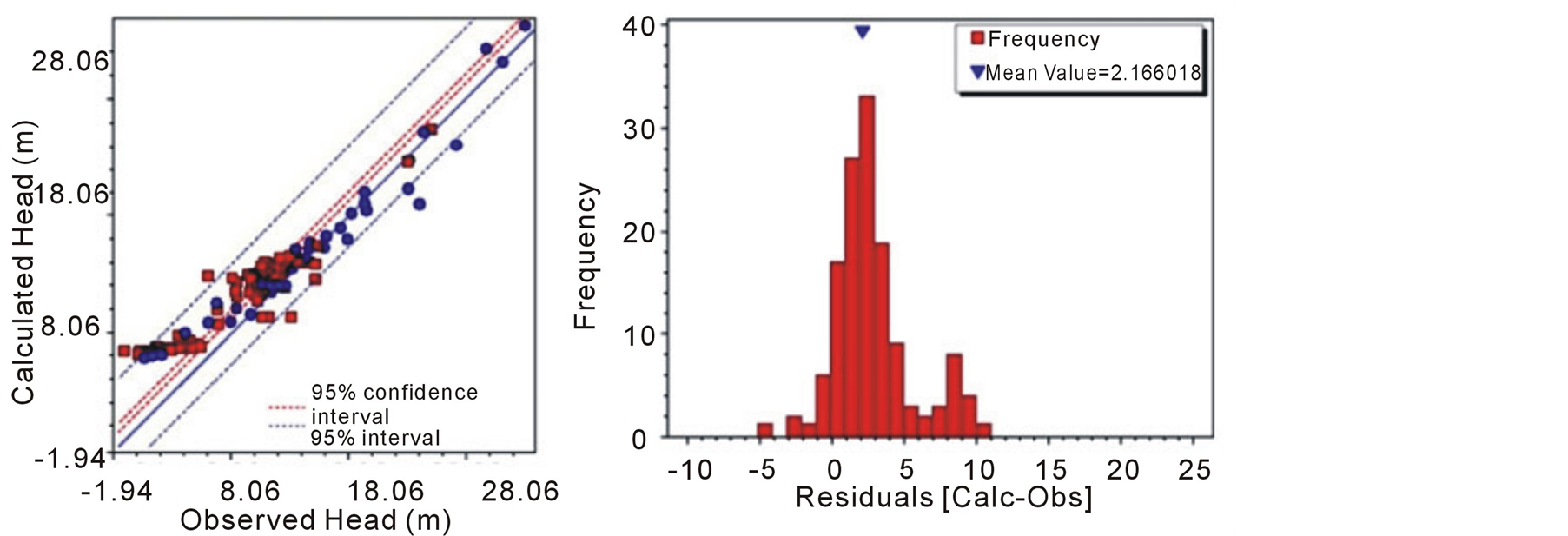 (b)
(b)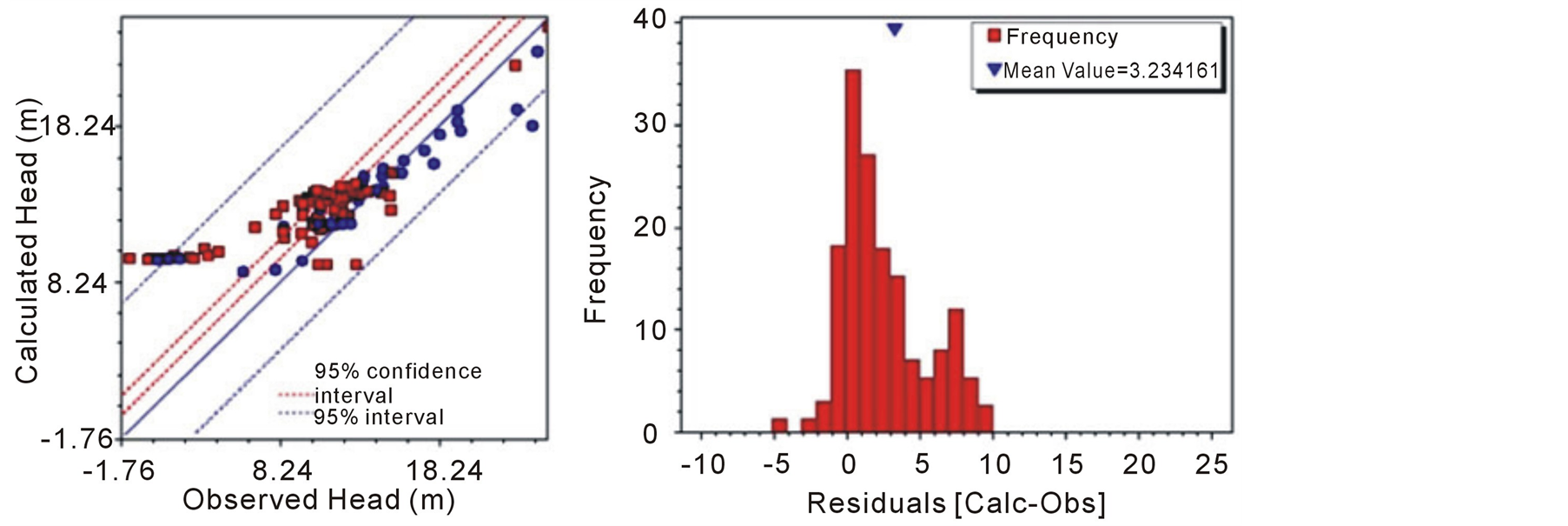 (c)
(c)
Figure 11. Calculated vs. Observed heads scatter plots (red squares: observed wells for lower aquifer; blue dots: observed wells in upper aquifer) and respective frequency histograms of calibration residuals of best calibrated models: (a) Model a-3; (b) Model b-2; (c) Model c-2.
sensitive variations for hydraulic heads in the observed wells (Figure 12(b) and Figure 12(c)). This restricted the set of possible hydrodynamic parameters for calibrating the models, minimizing the residual values. In particular, the “C” models were less sensitive to K variations than the “B” models, reducing the degrees of freedom of the parameters associated with acceptable model solutions (Figure 12(b)).
Finally, calibration issue is not so much due to a bias factor, related to the simulation model utilized, rather to the inability to represent the characteristics of geological heterogeneity at a larger scale. This limitation could be inherent to the numerical flow modeling since a homogeneous distribution of stratigraphic data is lacking, al-

Figure 12. Solutions of models (a) (Homogeneous), (b) (MC), and (c) (SIS) for different K values. Average water table data for the period 2006-2008 are plotted (observed values).




Figure 13. Groundwater flow simulation results for three different scenarios: S) facies classes simulation, M) groundwater flow model. Types of reservoir assumption: 1) homogeneous medium, 2) HGU simulated by a MC, 3) HGU simulated by SIS.
though abundant in the whole, but input data affect the quality of the solution in terms of calibration, as often happens in hydrogeological studies.
Analyzing the model solutions that produced the lowest residuals, the water table of Model A5 (Figures 13(S1)-(M1)) is West-East oriented. The main groundwater flow paths corresponded to the Simeto River’s palaeo-drainage, which corresponded to the main depocenter of sedimentary basin, whereas secondary paths came from both the Terreforti Hills and Mt. Iblei, as reconstructed by hydrogeological conceptual model.
Large continuous lithological bodies with different K values were simulated by the MC, highly affecting the groundwater flow simulation in Model B4 (Figures 13(S2)-(M2)) and creating equipotential lines that alternate phreatic and confined areas (Figure 13(M2)).
Model C3 (Figures 13(S3)-(M3)) highlighted that both the scarce continuity of the calculated sedimentary structures, especially the lowly permeable ones (clays), and clays and sands sediments interdigitating depositions smoothed the groundwater confining effect in the northern-central part of the aquifer, creating water table zones characteristic of homogeneous models (Figure 13(M3), eastern-central area).
All models showed a moderate hydraulic gradient in the central part of the CPQA, increasing up to 0.1% in the Terreforti Hills. For all the simulated scenarios, both the Simeto River and the Gornalunga River drained superficial groundwater in the central part of the CPQA, where the water table is deeper without streams interferences (Figure 13(M1)). The Dittaino River and the lower portion of the Simeto Rivers slightly recharged the groundwater (Figures 13(M2) and (M3)). All the simulated scenarios are equal at the Terreforti Hills, most likely due to the high hydraulic gradient that maintains constant groundwater flow paths independent of the lithofacies distribution.
5. Conclusions
A set of both plausible and equiprobable solutions of the complex geological structure of the alluvial reservoir of the Plain of Catania was achieved by means of different stochastic simulations techniques. In particular, starting from the same geognostic data, two spatial statistical interpolating methods based on alternative techniques of simulation were utilized. This work provides useful indications concerning both the limits and potentialities of these methods relating to their implications in hydrogeological mathematics. Hydraulic conductivity probabilistic fields were generated by means of two structure-imitating methods, MC and SIS. Moreover, the non-parametric simulation methods chosen allowed the handling of categorical variables such as HGUs without mathematical assumptions on the starting distributions (as other methods, like Gaussian-based ones, do) that would altered both the distribution of the raw data and the simulation result.
The solutions of the geostatistical models constituted de facto the range of possible equiprobable spatial models of the alluvial basin, but they were post-processed to synthesize the most probable heterogeneities configuration. Obviously, this statistical summary caused variations in the frequency distribution of the solutions, even if it was assessed how the post-processed result diverged from equiprobable solutions equally likely, and if the flow field could be simulated in spite of a simplification of the procedure that would have concerned a groundwater flow simulation for each geostatistical realization of the hydraulic conductivity field. Anyway, mode post-processing procedure leaded to reduce the complexity of the analysis by introducing, of course, a simplification and also a possible error, even if by analyzing the differences between the individual realizations and the post-processed only a slightly divergence of the mode configuration from the individual equiprobable was highlighted. In fact, these synthesized heterogeneity fields were utilized in implementing the CPQA groundwater flow model to assess the effects of uncertainty on hydraulic conductivity fields and then simulate predictions for groundwater behavior. The hydrodynamic parameter optimization of different geostatistical simulation methods was obtained by means of a calibration procedure (process imitating).
This study noted that the choice of geostatistical methods was fundamental for groundwater flow numerical simulation to represent, at best, both geological structure continuity and hydraulic conductivity at different scales. In fact, numerical model solutions could not be improved during calibration, especially in the heterogeneity models non-representative of continuous sedimentary structures, such as those produced by SIS. A geological system calculated with a poor hydraulic connection among structures at a macro-scale reference yielded groundwater flow models with erratic solutions similar to homogeneous systems.
The geometric features of the aquifer medium were not reproduced by different geostatistical methods at the same scale and detail. In particular, the SIS covariance model, although it fit the function of spatial variability, did not represent spatial continuity of the geological structures at a macro scale. By contrast, the geologic-based MC geostatistical model allowed the emphasis of geological macro-structures, generating continuous clay bodies in upper part of the CPQA aquifer and big sand lens in the lower one. Computations were not only complicated by huge scale difference between the horizontal and vertical planes but also by a deformed three-dimensional grid, which also made spatial analysis difficult. This framework is frequently simplified by choosing regular grids; however, this is inappropriate for representing complex geological volumes such as the CPQA sedimentary basin.
In real systems containing specific geological heterogeneity, such as more conductive layers and intercomnected networks and paleochannels, the application of models based on the spatial covariance (such as SIS) may be inadequate for reproducing the macrostructures. By contrast, the geostatistical geologic model-based methods (MC) allow reconstruction and emphasize the heterogeneity of geological characterizations, even if it neglects heterogeneity at the scale chosen to represent the CPQA heterogeneity, i.e. the cell size of the discretization grid. The MC geologic model can reproduce an adequate spatial connection of lithofacies. In addition MC simulations, yielded by T-PROGS, represent a more realistic solution dealing to the proposed geological model (reference image), and they determines a reduced uncertainty in the solution of the model flow.
A not regular volume such as the 12 layers deformed grid hosting both MC and SIS simulations complicates the calculation of solutions in the portions of the modeled volume where layers thicknesses decreased, with scarce vertical contiguousness between adjacent cells. Moreover, all the simulated models tended to over-predict the hydraulic heads. The correlation coefficients of the calculated heads and the observed ones were not close to the minimum values necessary to consider a model predictive, except with Model B. There were greater residuals close to the seacoast and in Catania’s industrial area due to the uncertainty of both the sample values and the measured heads. The large amount of pumping and geometrical complexity of the hydrogeological system in the coastal area introduce uncertainties in the implemented models, which can be improved only after performing new piezometric fieldwork and defining actual wells discharges.
Acknowledgements
The Authors are indebted to Prof. Vincenzo Ferrara (University of Catania, Italy), Prof. Luigi Carmignani and Prof. Gianluca Cornamusini (CGT Center for GeoTechnologies—University of Siena, Italy), which helped them in several parts of this work. This work was supported by grants MIUR 2005 (scientific responsible: Giovanna Pappalardo).
References
- Ferrara, V. and Pappalardo, G. (2004) Intensive Exploitation Effect on the Alluvial Aquifer of the Catania Plain, Eastern Sicily, Italy. Geofísica Internacional, 43, 671-681.
- Ferrara, V., Pappalardo, G. and Rapisarda, F. (2007) Salinization Factors Affecting the Coastal Aquifers in Eastern Sicily. In: Pulido Bosh, A., Lòpez Getay, J.A. and Ramos Gonzalez, G., Eds., Los acuiferos costeros: Retos y soluciones (TIAC ’07), Almeira, 16-19 October 2007, Instituto Geològico y Minero de Espana, Serie Hidrogeologia y Aguas Subterraneas, Vol. 23, 105-116, Madrid.
- Ababou, R., McLaughlin, D., Gelhar, L.W. and Tompson, A.F.B. (1989) Numerical Simulation of Three-Dimensional Saturated Flow in Randomly Heterogeneous Porous Media. Transport in Porous Media, 4, 549-565.
- Webb, E.K. and Anderson, M.P. (1996) Simulation of Preferential Flow in Three-Dimensional, Heterogenous Conductivity Fields with Realistic Internal Architecture. Water Resources Research, 32, 533-545. http://dx.doi.org/10.1029/95WR03399
- de Marsily, G., Delay, F., Teles, V. and Schafmeister, M.T. (1998) Some Current Methods to Represent the Heterogeneity of Natural Media in Hydrogeology. Hydrogeology Journal, 6, 115-130. http://dx.doi.org/10.1007/s100400050138
- Scheibe, T.D. and Yabusaki, S. (1998) Scaling of Flow and Transport Behavior in Heterogeneous Groundwater Systems. Advances in Water Resources, 22, 223-238. http://dx.doi.org/10.1016/S0309-1708(98)00014-1
- Labolle, E. and Fogg, G. (2001) Role of Molecular Diffusion in Contaminant Migration and Recovery in an Alluvial Aquifer System. Transport in Porous Media, 42, 155-179. http://dx.doi.org/10.1023/A:1006772716244
- Fleckenstein, J.H., Neiswonger, R.G. and Fogg, G. (2006) River-Aquifer Interactions, Geologic Heterogeneity and Low Flow Management. Groundwater, 44, 837-852. http://dx.doi.org/10.1111/j.1745-6584.2006.00190.x
- Eaton, T. (2006) On the Importance of Geological Heterogeneity for Flow Simulation. Sedimentary Geology, 184, 187- 201. http://dx.doi.org/10.1016/j.sedgeo.2005.11.002
- Koltermann, C.E. and Gorelik, S.M. (1996) Heterogeneity in Sedimentary Deposits: A Review of Structure-Imitating, Process-Imitating and Descriptive Approaches. Water Resources Research, 32, 2617-2658. http://dx.doi.org/10.1029/96WR00025
- Lee, S.Y., Carle, S.F. and Fogg, G.E. (2007) Geologic Heterogeneity and a Comparison of Two Geological Models: Sequential Gaussian and Transition-Probability-Based Geostatistical Simulation. Advances in Water Resources, 30, 1914- 1932. http://dx.doi.org/10.1016/j.advwatres.2007.03.005
- Gómez-Hernández, J.J. and Wen, X.H. (1998) To Be or Not to Be Multi-Gaussian? A Reflection on Stochastic Hydrogeology. Advances in Water Resources, 21, 47-61. http://dx.doi.org/10.1016/S0309-1708(96)00031-0
- Alabert, F.G. and Modot V. (1993) Stochastic Models of Reservoir Heterogeneity: Impact on Connectivity and Average Permeabilities. SEG Technical Program Expanded Abstracts, 340.
- Dell’Arciprete, D., Bersezio, R., Felletti, F., Giudici, M., Comunian, A. and Renard, P. (2012) Comparison of Three Geostatistical Methods for Hydrofacies Simulation: A Test on Alluvial Sediments. Hydrogeology Journal, 20, 299-311. http://dx.doi.org/10.1007/s10040-011-0808-0
- Carle, S.F. (1999) T-PROGS: Transition Probability Geostatistical Software. Version 2.1. University of California, Davis.
- Weissman, G.S., Carle, S.F. and Fogg, G.E. (1999) Three-Dimensional Hydrofacies Modeling Based on Soil Surveys and Transition Probability Geostatistics. Water Resources Research, 35, 1761-1770. http://dx.doi.org/10.1029/1999WR900048
- Granati, C. (2007) Ricostruzione degli acquiferi della Bassa Pianura Friulana e simulazione di flusso con approccio stocastico (Reconstruction of aquifers of Southern Plain of Friuli region and stochastic flow simulation). Ph.D. Thesis, University of Udine, Udine.
- Lou, J. (1996) Transition Probability Approach to Statistical Analysis of Spatial Qualitative Variables in Geology. In: Forster, A. and Merriam, D.F., Eds., Geologic Modeling and Mapping, Plenum Press, New York, 281-299.
- Elfeki, A.M. and Dekking, F.M. (2001) A Markov Chain Model for Subsurface Characterization: Theory and Applications. Mathematical Geology, 33, 569-589. http://dx.doi.org/10.1023/A:1011044812133
- Li, W., Zhang, C., Burt, J.E., Zhu, A.X. and Feyen, J. (2004) Two-Dimensional Markov Chain Simulation of Soil Type Spatial Distribution. Soil Science Society of America Journal, 68, 1479-1490. http://dx.doi.org/10.2136/sssaj2004.1479
- Li, W.D. and Zhang, C.R. (2008) A Single-Chain-Based Multidimensional Markov Chain Model for Subsurface Characterization. Environmental and Ecological Statistics, 15, 157-174. http://dx.doi.org/10.1007/s10651-007-0045-9
- Li, W.D. (2006) Transiogram: A Spatial Relationship Measure for Categorical Data. International Journal of Geographical Information Science, 20, 693-699. http://dx.doi.org/10.1080/13658810600607816
- Pardo-Igúzquiza, E. and Dowd, P.A. (2005) Multiple Indicator Cokriging with Application to Optimal Sampling for Environmental Monitoring. Computers & Geosciences, 31, 1-13. http://dx.doi.org/10.1016/j.cageo.2004.08.006
- Goovaerts, P. (1997) Geostatistics for Natural Resources Evaluation. Oxford University, Oxford.
- Deutsch, C.V. and Journel, A.G. (1998) GSLIB: Geostatistical Software Library and User’s Guide. 2nd Edition, Oxford University Press, New York.
- Seifért, D. and Jensen, J.L. (1999) Sequential Indicator Simulation as a Tool in Reservoir Description: Issues and Uncertainties. Mathematical Geology, 31, 527-550. http://dx.doi.org/10.1023/A:1007563907124
- Pardo-Iguzquizaa, E. and Dowd, P.A. (2005) Multiple Indicator Cokriging with Application to Optimal Sampling for Environmental Monitoring. Computers & Geosciences, 31, 1-13. http://dx.doi.org/10.1016/j.cageo.2004.08.006
- Harbaugh, A., Banta, E., Hill, M. and McDonald, M. (2000) MODFOLW-2000, The US Geological Survey Modular Ground-Water Model. User Guide to Modularization Concepts and the Ground-Water Flow Process. Open-File Report 00-92 U.S. Geological Survey, Reston.
- Lentini, F. (1982) The Geology of the Mt. Etna Basement. Memorie della Società Geologica Italiana, 23, 7-26.
- Ben-Avraham, Z., Boccaletti, M., Cello, G., Grasso, M., Lentini, F., Torelli, L. and Tortorici, L. (1990) Principali domini strutturali originatisi dalla collisione continentale neogenico-quaternaria nel Mediterraneo centrale (Main Structural Domains Deriving from Neogene-Quaternary Continental Collision in Central Mediterranean Sea). Memorie della Società Geologica Italiana, 45, 453-462.
- Lentini, F., Catalano, S. and Carbone, S. (1996) The External Thrust System in Southern Italy: A Target for Petroleum Exploration. Petroleum Geoscience, 2, 333-342. http://dx.doi.org/10.1144/petgeo.2.4.333
- Grasso, M. (1993) Pleistocene Structures along the Ionian Side of the Hyblean Plateau (SE Sicily): Implications for the Tectonic Evolution of the Malta Escarpment. UNESCO Reports in Marine Science, 58, 49-54, Paris.
- Torelli, L., Grasso, M., Mazzoldi, G. and Peis, D. (1998) Plio-Quaternary Tectonic Evolution and Structure of the Catania Foredeep, the Northern Hyblean Plateau and the Ionian Shelf (SE Sicily). Tectonophysics, 298, 209-221.
- Butler, R.W.H. and Grasso, M. (1993) Tectonic Controls on Base-Level Variations and Depositional Sequences within Thrust-Top and Foredeep Basins: Examples from the Neogene Thrust Belt of Central Sicily. Basin Research, 5, 137- 151. http://dx.doi.org/10.1111/j.1365-2117.1993.tb00062.x
- Longhitano, S. and Colella, A. (2002) Stratigraphy and Basin-Fill Architecture of a Plio-Pleistocene Foredeep Basin (Catania Plain, Eastern Sicily): A Preliminary Synthesis. Geoacta, 1, 111-130.
- Francaviglia, A. (1962) L’imbasamento sedimentario dell’Etna e il Golfo preetneo. Bollettino Servizio Geologico Italiano, 81, 593-684.
- Wezel, F.C. (1967) I terreni quaternari del substrato dell’Etna (Quaternary sediments of Mt. Etna bedrock). Atti dell’Accademia Gioenia di Scienze Naturali, Catania, 6, 279-293.
- Lanzafame, G., Neri, M., Coltelli, M., Lodato, L. and Rust, D. (1997) North-South Compression in the Mt. Etna Region (Sicily): Spatial and Temporal Distribution. Acta Vulcanologica, 9, 121-133.
- Carbone, S., Lentini, F., Branca, S., Barbano, M.S., Ferrara, V. and Pappalardo, G. (2010) Note illustrative della Carta geologica d'Italia alla scala 1:50.000 Foglio 633 Paternò (Description of Geological Map of Italy at 1:50.000 scale, Sheet No. 633 “Paternò”). ISPRA (Istituto Superiore per la Protezione e la Ricerca Ambientale SERVIZIO GEOLOGICO D’ ITALIA), Rome.
- ENI (1992) Acque dolci sotterranee: Inventario dei dati raccolti dall'AGIP durante la ricerca di idrocarburi in Italia. ENI Ente Nazionale Idrocarburi, Rome.
- Labaume, P., Bousquet, J.C. and Lanzafame, G. (1990) Early Deformations at a Submarine Compressive Front: The Quaternary Catania Foredeep South of Mt. Etna, Sicily. Tectonophysics, 177, 349-366.
- Accordi, B. and Francaviglia, A. (1960) La geologia del Bacino del Simeto (Geology of Simeto River Basin). Tecnica Agricola, 12, 221-244.
- Kieffer, G. (1971) Dépots et niveaux marins et fluviatiles de la région de Catane (Sicile). (Marine and Fluvial Deposits of Catania Area, Sicily). Méediterraneée, 2, 591-626. http://dx.doi.org/10.3406/medit.1971.1387
- Breusse, J. and Huot, G. (1954) Hydrogeological Survey in the Catania Area by Means of Electrical Soundings. Geophysical Prospecting, 2, 227-231.
- Bianchi, F., Carbone, S., Grasso, M., Invernizzi, G., Lentini, F., Longaretti, G., Merlini, S. and Mostardini, F. (1987) Sicilia orientale: Profilo geologico Nebrodi-Iblei (Eastern Sicily: Geological Profile of Nebrodi-Iblei Mountains Chain). Memorie della Società Geologica Italiana, 38, 429-458.
- Goodale, C.L., Aber, J.D. and Ollinger, S.V. (1998) Mapping Monthly Precipitation, Temperature and Solar Radiation for Ireland with Polynomial Regression and a Digital Elevation Model. Climate Research, 10, 35-49. http://dx.doi.org/10.3354/cr010035
- Bianca, M., Monaco, C., Tortorici, L. and Cernobori, L. (1999) Quaternary Normal Faulting in Southeastern Sicily (Italy): A Seismic Source for the 1693 Large Earthquake. Geophysical Journal International, 139, 370-394. http://dx.doi.org/10.1046/j.1365-246x.1999.00942.x
- Ferrara, V. (1999) Presentazione della carta di Vulnerabilità all’inquinamento dell'acquifero alluvionale della Piana di Catania (Sicilia NE). (Presentation of Vulnerability Map of Aquifer of Catania Alluvial Plain). Proceedings of 3rd National Conference on Protection and Management of Groundwater for the III Millenium, Parma, 13-15 October 1999, pp. 99-104
- Tortorici, G., De Guidi, G. and Sturiale, G. (2006) Evoluzione tettonica quaternaria del margine settentrionale del Plateau Ibleo (Sicilia sud-orientale). (Quaternary Tectonic evolution of Northern margin of Iblean Plateau, South-Eastern Sicily). Bollettino Società Geologica Italiana, 125, 21-37.
- Costa, N. (2008) Modello geologico-idrogeologico dell'acquifero della piana di Catania e valutazione delle risorse idriche sotterranee (Geological and Hydrogeological Model of Acquifer of Catania Plain and Groundwater Resources Evaluation). Ph.D. Thesis, University of Catania, Catania.
- Maji, R., Sudicky, E.A., Panday, S. and Teutsch, G. (2006) Transition Probability/Markov Chain Analysis of DNAPL Source Zone and Plumes. Groundwater, 44, 853-863. http://dx.doi.org/10.1111/j.1745-6584.2005.00194.x
- Ye, M. and Khaleel, R. (2008) A Markov Chain Model for Characterizing Medium Heterogeneity and Sediment Layering Structure. Water Resources Research, 44, 1-15. http://dx.doi.org/10.1029/2008WR006924
- Middleton, G.V. (1973) Johannes Walther’s Law of the Correlation of Facies. Geological Society of America Bulletin, 84, 979-987. http://dx.doi.org/10.1130/0016-7606(1973)84<979:JWLOTC>2.0.CO;2
- Goovaerts, P. (2000) Estimation or Simulation of Soil Properties? An Optimization Problem with Conflicting Criteria. Geoderma, 97, 165-186. http://dx.doi.org/10.1016/S0016-7061(00)00037-9
- Felletti, F., Bersezio, R. and Giudici, M. (2006) Geostatistical Simulation and Numerical Upscaling, to Model Ground- Water Flow in a Sandy-Gravel, Braided River, Aquifer Analogue. Journal of Sedimentary Research, 76, 1215-1229. http://dx.doi.org/10.2110/jsr.2006.091
- Geovariances (2010) ISATIS User’s Guide. Ecole des Mines & Geovariances. Geovariances, Avon.
- Civita, M. (2005) Idrogeologia applicata ed ambientale (Applied and Environmental Hydrogeology). Casa Editrice Ambrosiana, Milan.
- Cerbini, G. and Gorla, M. (2009) Idrogeologia applicata, principi metodi e misure (Applied Hydrogeology: Methods and Measures). Edizioni Geo-Impianti, Segrate, Milan.
- Spitz, K. and Moreno, J. (1996) A Practical Guide to Groundwater and Solute Transport Modeling. John Wiley & Sons, Inc., New York.
- MacDonald, M.G. and Harbaugh, A. (1988) A Modular Three Dimensional Finite-Difference Ground-Water Flow Model. Techniques of Water-Resources Investigations of the US Geological Survey, Vol. 6, Book 6, Ch. A1, US Government Printing Office, Washington DC.
- USDA-SCS (1985) National Engineering Handbook. Section 4-Hydrology. USDA-SCS, Washington DC.
- Turc, L. (1954) Le bilan d’eau des sols. Relation entre la précipitation, l'évaporation et l'écoulement. Annales Agronomiques, 5, 491-569.
- Webster, R. and Oliver, M.A. (2001) Geostatistics for Environmental Scientists (Statistics in Practice). John Wiley and Sons, Ltd., Chichester.


