Journal of Software Engineering and Applications
 Vol.5 No.4(2012), Article ID:18575,6 pages DOI:10.4236/jsea.2012.54034

Classification of Web Services Using Bayesian Network

Ramakanta Mohanty1*, V. Ravi2, M. R. Patra3

1Computer Science Department, MLR Institute of Technology, Hyderabad, India; 2Institute for Development and Research in Banking Technology, Hyderabad, India; 3Computer Science Department, Berhampur University, Berhampur, India.

Email: *ramakanta5a@gmail.com, rav_padma@yahoo.com, mrpatra12@gmail.com

Received December 17th, 2011; revised January 31st, 2012; accepted February 15th, 2012

Keywords: Web Services; Quality of Services (QoS); Bayesian Network; Naïve Based Bayesian; Markov Blanket and Tabu Search

ABSTRACT

In this paper, we employed Naïve Bayes, Markov blanket and Tabu search to rank web services. The Bayesian Network is demonstrated on a dataset taken from literature. The dataset consists of 364 web services whose quality is described by 9 attributes. Here, the attributes are treated as criteria, to classify web services. From the experiments, we conclude that Naïve based Bayesian network performs better than other two techniques comparable to the classification done in literature.

1. Introduction

Services are tendered and availed in almost all the business and industries. The growth and proliferation of IT across industries and business appear to have fuelled the requirement as well as the delivery of services profoundly. Delivering services has been an attractive business proposition for many industries lately. The latest development in the systems is a new paradigm, called web services [1]. Web Services heralded another significant mile stone in the history of IT. Earlier, Internet catered mostly to the business to Customer (B2C) category of the users on the web. As against this, Web Services enable B2B interaction as well Web. They are independent of platform and natural languages, which is suitable for accessing from heterogeneous environments. With the rapid introduction of web services technologies, researchers focused more on the functional and interfacing aspects of web services, which include HTTP and XMLbased messaging. They are used to communicate by employing pervasive standards based web technologies. Web services are based on XML and three other core technologies: WSDL, SOAP, and UDDI. WSDL is a document which describes the services’ location on the web and the functionality the service provides. Information related to the web service is to be entered in a UDDI registry, which permits web service consumers to find out and locate the services they required. With the help of the information available in the UDDI registry based on the web services, client developer uses instructions in the WSDL to construct SOAP messages for exchanging data with the service over HTTP attributes [2].

In this study, we address this problem of efficiently identifying a set quality attributes by employing Bayesian Networks vz. Naive Bayes, Markov blanket and Tabu search. Naive Bayes is special form of Bayesian network that is widely used for classification [3] and clustering [4], but its potential for general probabilistic modeling (i.e., to answer joint, conditional and marginal queries over arbitrary distributions) remains largely unexploited. Naive Bayes represents a distribution as a mixture of components, where within each component all variables are assumed independent of each other. The Markov blanket of a variable Y, (MB(Y)), by definition, is the set of variables such that Y is conditionally independent of all the other variables given MB(Y). A Markov Blanket Directed Acyclic Graph (MB DAG) is a Directed Acyclic Graph over that subset of variables. When the parameters of the MB DAG are estimated, the result is a Bayesian Network, defined in the next section. Recent research by the machine learning community [5-7] has sought to identify the Markov blanket of a target variable by filtering variables using statistical decisions for conditional independence and using the MB predictors as the input features of a classifier. However, learning MB DAG classifiers from data is an open problem [8]. There are several challenges: the problem of learning the graphical structure with the highest score (for a variety of scores) is NP hard [8] for methods that use conditional independencies to guide graph search, identifying conditional independencies in the presence of limited data is quite unreliable and the presence of multiple local optima in the Tabu search Enhanced Markov blanket Classifier space of possible structures makes the search process difficult.

Classification using the Markov blanket of a target variable in a Bayesian Network has important properties. It specifies a statistically efficient prediction of the probability distribution of a variable from the smallest subset of variables that contains all of the information about the target variable, it provides accuracy while avoiding over fitting due to redundant variables and it provides a classifier of the target variable from a reduced set of predictors. The TS/MB procedure proposed in this paper allows us to move through the search space of Markov blanket structures quickly and escape from local optima, thus learning a more robust structure.

The rest of paper is organized as follows: Section 2 presents the quality issues in web services and QWS dataset. Section 3 describes the overview of Bayesian Network Section 4 presents the results and discussions, and Section 5 concludes the paper.

2. Quality Issues in Web Services

QoS plays an important role in finding out the performance of web services. Earlier, QoS has been used in networking and multimedia applications. Recently, there is a trend in adopting this concept to web services [9]. The basic aim is to identify the QoS attributes [10-12] for improving the quality of web services through replication services [10], load distribution [13], and service redirection [14]. To measure the QoS of a web service, attributes like Response Time, Throughput, Availability, Reliability, Cost, and Response Time are considered.

2.1. QoS Attributes

According to Kalepu et al. [15], quality of service (QoS) is a combination of several qualities or properties of a service, such as: 1) Availability; 2) Reliability; 3) Price; 4) Throughput; 5) Response Time; 6) Latency; 7) Performance; 8) Security; 9) Regulatory; 10) Accessibility; 11) Robustness/Flexibility; 12) Accuracy; 13) Servability; 14) Integrity and 15) Reputation. QoS parameters determine the performances of the web services and find out which web services are best and meet user’s requirements.

Users of web services are not human beings but programs that send requests for services to web service providers. QoS issues in web services have to be evaluated from the perspective of the providers of web services (such as the airline-booking web service) and from the perspective of the users of these services (in this case, the travel agent site) [16]. There are other models available related to the quality of web services issues. A QoS model [16] represented in Table 1 shows that the main classification of QoS attributes is based on internal attributes, which are independent of the service environment, and external attributes that are dependent on the service environment. The attributes of the model in Table 1 are almost similar to the attributes of QWS Dataset used in this paper.

2.2. Description of QWS Dataset

QWS dataset [17] consists of different web service implementations and their attributes as presented in Table 2. The classification is measured based on the overall quality rating provided by all the attributes. The functionality of the web services can be helpful to differentiate between various services. The attributes G1 to G10 are used as explanatory variables and the attribute G11 is used as the target variable. However, attributes G12 and G13 are ignored as they do not contribute to the analysis.

The web services [1,2] in the QWS dataset are classified into four categories, such as: 1) Platinum (high quality); 2) gold; 3) silver and 4) bronze (low quality). The classification is measured based on the overall quality rating provided by WSRF. It is grouped into a particular web service based on classification. The functionality of the web services can be helpful to differentiate between various services [14].

3. Overview of Bayesian Networks

A Bayesian network is a directed acyclic graph model that represents conditional independencies between a set of variables [18,19]. It has two constituents: One is a network graphical structure which is a directed acyclic graph with the nodes of variables and arcs of relations. The other is the conditional probability table associated with each node in the model graph. Machine learning techniques are able to estimate the structure and the conditional probability table from the training data. Based on the Bayesian probability inference, the conditional probability can be estimated from the statistical data and propagated along the links of the network structure to the target label. By setting a threshold of confidence, the final probability value can be used as the indication for the classification decision. The Bayesian formula can be mathematically expressed as below:

(1)

According to the basic statistical theory, e.g., the Chain Rule and independency relation derived from the network structure, the joint probability of 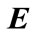can be

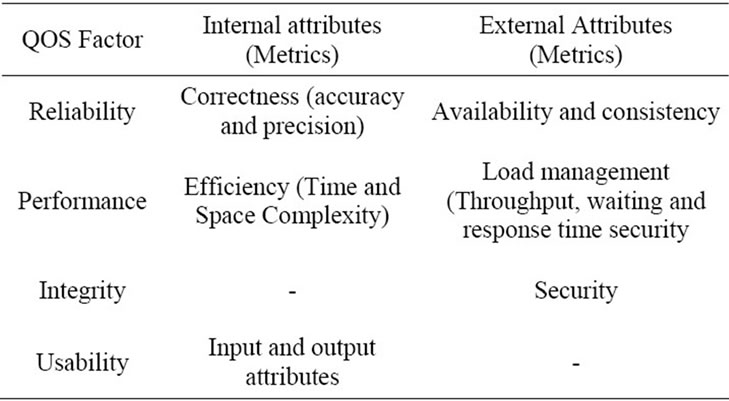
Table 1. QoS model of web services [4].

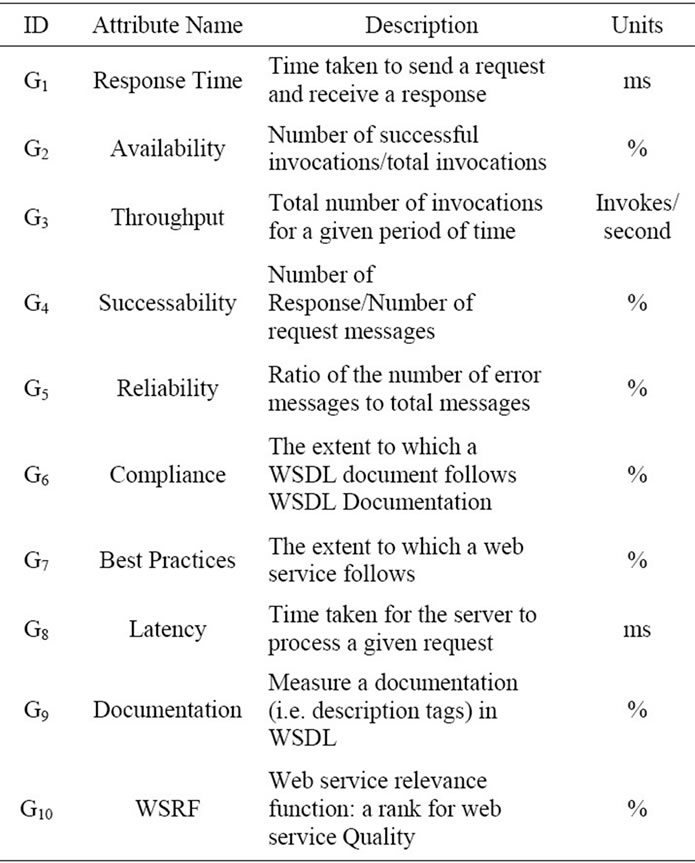
Table 2. Attributes of QWS dataset.

calculated by the production of local distributions with its parent nodesi.e.

(2)

In the above formulas, denotes a set of variable values, i.e. 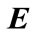= {E1, E2, ···,En}. H is termed as hypothesis. H is called the prior probability and is called posteriori probability of H given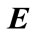. If Ei has no parent nodes, is equal to P(Ei).

3.1. Naïve Bayes

Naive Bayes models are so named for their “naive” assum-ption that all variables Xi are mutually independent given a “special” variable C. The joint distribution is then given compactly by P(C, X1, ···, Xn) =. The univariate conditional distributions P(Xi|C) can take any form (e.g., multinomial for discrete variables, Gaussian for continuous ones). When the variable C is observed in the training data, naive Bayes can be used for classification, by assigning test example (X1, ···, Xn) to the class C with highest P(C|X1, ···, Xn) [2]. When C is unobserved, data points (X1, ···, Xn) can be clustered by applying the EM algorithm with C as the missing information, each value of C corresponds to a different cluster, and P(C|X1, ···, Xn) is the point’s probability of membership in cluster C [14]. Naive Bayes models can be viewed as Bayesian networks in which each Xi has C as the sole parent and C has no parents. A naive Bayes model with Gaussian P(Xi|C) is equivalent to a mixture of Gaussians with diagonal covariance matrices. While mixtures of Gaussians are widely used for density estimation in continuous domains, naive Bayes models have seen very little similar use in discrete and mixed domains. However, they have some notable advantages for this purpose. In particular, they allow for very efficient inference of marginal and conditional distributions. To see this, let X be the set of query variables, Z be the remaining variables, and k be the number of mixture components (i.e., the number of values of C). We can compute the marginal distribution of X by summing out C and Z:

where the last equality holds because, for all j, 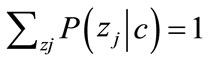Thus the non-query variables Z can simply be ignored when computing P(X = x), and the time required to compute P(X = x) is O(|X|k), independent of |Z|. This contrasts with Bayesian network inference, which is worst-case exponential in |Z|. Similar considerations apply to conditional probabilities, which can be computed efficiently as ratios of marginal probabilities:. A slightly richer model than naive Bayes which still allows for efficient inference is the mixture of trees, where, in each cluster, each variable can have one other parent in addition to C. The basic graph of Bayesian network is presented in Figure 1 and the graph of QWS dataset for naïve Bayes are depicted in Figure 3.

3.2. Markov Blanket

The Markov condition implies that the joint distribution P can be factorized as a product of conditional probabilities, by specifying the distribution of each node conditional on its parents [20]. In particular, for a given DAG S, the joint probability distribution for X can be written as

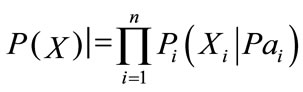(3)

where Pai denotes the set of parents of Xi in S; this is called a Markov factorization of P according to S. The set of distributions represented by S is the set of distributions that satisfy the Markov condition for S. If P is faithful to the graph S, then given a Bayesian Network (S, P), there is a unique Markov blanket for Y consisting of PaY , the set of parents of Y, chY , the set of children of Y, and Pa chY , the set of parents of children of Y .

For example, consider the two DAGs in Figures 1 and 2, above. The factorization of P entailed by the Bayesian Network (S, P) is

(4)

The factorization of the conditional probability p(Y |X1, ···, X6) entailed by the Markov blanket for Y corresponds to the product of those (local) factors in equation (2) that contain the term Y .

(5)

The graph of QWS dataset is depicted in Figure 5 for Markov blanket of Bayesian networks.

3.3. Tabu Search

A Heuristic is an algorithm or procedure that provides a shortcut to solve complex decision problems. Heuristics are used when you have limited time and/or information to make a decision. For example, some optimization problems, such as the travelling salesman problem, may take far too long to compute an optimal solution. A good heuristic is fast and able find a solution that is no more than a few percentage points worse than the optimal solution. Heuristics lead to good decisions most of the time, but not always. There have been several Meta-heuristic applications recently in Machine Learning, Evolutionary Algorithms, and Fuzzy Logic problems. Tabu Search is a meta-heuristic strategy that is able to guide traditional local search methods to escape the trap of local optimality with the assistance of adaptive memory [21]. Its strategic use of memory and responsive exploration is based

Figure 1. The Bayesian network (S, P).

Figure 2. A Markov blanket DAG for Y.

Figure 3. QWS dataset for Naïve Bayes bayesian network.

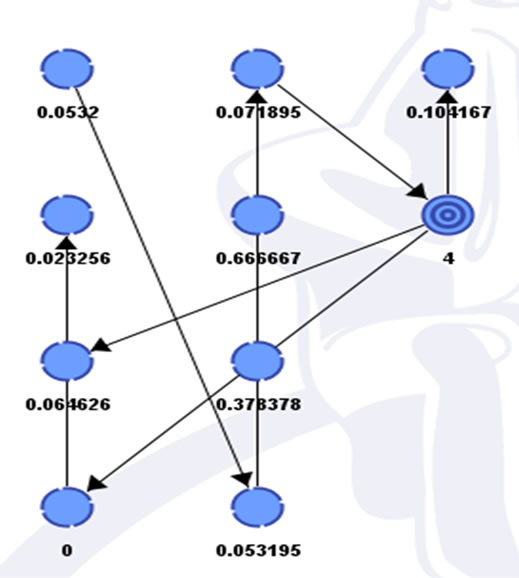
Figure 4. QWS dataset for Tabu search.

Figure 5. QWS dataset for Markov blanket bayesian network.

on selected concepts that cut across the fields of artificial intelligence and operations research.

Tabu list (TL) is given by

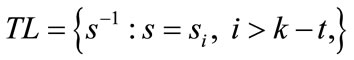(6)

where k is the iteration index and s−1 is the inverse of the move s; i.e., s−1(s(x)) = x. In words, TL is the set of those moves that would undo one of those moves in the t most recent iterations. t is called the Tabu tenure.

The use of TL provides the “constrained search” element of the approach, and hence the solution generated depends critically on the composition of TL and the way it is updated. Tabu search makes no reference to the condition of local optimality, except implicitly where a local optimum improves on the best solution. A best move, rather than an improving move is chosen at each step. This strategy is embedded in the OPTIMUM function. Tabu search analysis of QWS attribute is depicted in Figure 4.

4. Results and Discussions

We employed Naïve Bayes, Markov blanket and Tabu search techniques to classify web services. We note that the average accuracy of Naïve Bayes classifier is 85.62%, followed by Tabu search of 82. 45% and Markov blanket of 81.36% presented in Table 3. In this context, we employed Back propagation trained neural network to find the importance of different attributes in web services. We found that we found that WRRF plays a vital role for classifying the web services. We excluded the WSRF from dataset and experimented. We observe that the average accuracy of Naïve Bayes is 75.01% and Marcov Blanket is 65.48% and Tabu serach is 71.38% presented in Table 4. As Bayesian network is a very good classifier to classify classification type of problems. In this context, the result obtained by Bayesian classifier is not superior

Table 3. Accuracies of bayesian network without removing wsrf.

Table 4. Accuracies of bayesian nework after removing wsrf.

to the results obtained by [22] to classify the accuracy of web services. As Bayesian network has not been applied to classify web services, we employed this approach in the present study.

5. Conclusion

We presented Naïve Bayes, Markov blanket and Tabu search to classify web services. We observed that Naïve Bays approach predicted better accuracy than Markov blanket and Tabu search. Secondly, Bayesian belief network is employed first time to classify web services in the present study. Future directions include more exploration of Markov blanket approach for rule generation and quality of attributes to decide the classification of web services.

6. Acknowledgements

We are grateful to Dr. E. Al-Masri and Dr. Q. H. Mahmoud for providing us the dataset related to the web services classification.

REFERENCES

  1. L. Z. Zeng, B. Benatallah, M. Dumas, J. Z. Kalagnanam and Q. Z. Sheng, “Web Engineering: Quality Driven Web Service Composition,” Proceedings of the 12th International Conference on World Wide Web, Budapest, 2003, pp. 411-421. doi:10.1145/775152.775211
  2. A. Tsalgatidou and T. Pilioura, “An Overview of Standards and Related Technology in Web Services,” Distributed and Parallel Database, Vol. 12, No. 2-3, 2002, pp. 135-162. doi:10.1023/A:1016599017660
  3. P. Domingos and M. Pazzani, “On the Optimality of the Simple Bayesian Classifier under Zero-One Loss”, Machine Learning, Vol. 29, No. 2-3, 1997, pp. 103-130. doi:10.1023/A:1007413511361
  4. P. Cheeseman and J. Stutz, “Bayesian Classification (Auto Class): Theory and Results,” Advances in Knowledge Discovery and Data Mining, Vol. 180, 1996, pp. 153-180.
  5. D. Margaritis, “Learning Bayesian Network Model Structure,” Technical Report CMU-CS-03-153, 2003.
  6. I. Tsamardinos, C. F. Aliferis and A. Statnikov, “LargeScale Feature Selection Using Markov Blanket Induction for the Prediction of Protein-Drug Binding,” Technical Report DSL-02-08, Vanderbilt University, Nashville, 2002.
  7. I. Tsamardinos, C. Aliferis, and A. Statnikov, “Algorithms for Largescale Local Causal Discovery in the Presence of Small Sample or Large Causal Neighborhood,” Technical Report DSL-02-08, Vanderbilt University, Nashville, 2002.
  8. D. M. Chickering, “Learning Equivalence Classes of Bayesian-Network Structures,” Journal of Machine Learning Research, Vol. 2, 2002, pp. 507-554.
  9. S. Vinoski, “Service Discovery 101,” Proceedings of Internet Computing Conference on IEEE, Vol. 7, No.1, 2003, pp. 69-71. doi:10.1109/MIC.2003.1167342
  10. G. V. Bochmann, B. Kerherve, H. Lutffiyya, M.-V. M. Salem and H. Ye, “Introducing QoS to Electronic Commerce Applications,” Proceedings of the 2nd International Symposium on Electronic Commerce (ISEC), HongKong, 26-28 April, 2001 pp. 138-147.
  11. A. Mani and A. Nagarajan, “Understanding Quality of Services for Web Services,” 2002. http://www-106.ibm.com/developerworks/library/ws-quality
  12. S. Ran, “A Model for Web Services Discovery with QoS,” ACM SIGecom Exchange, Vol. 4, No. 1, 2003. doi:10.1145/844357.844360
  13. M. Conti, E. Gregori and F. Panzieri, “Load Distribution among Replicated Web Services A: QoS Based Approach,” Second Workshop on Internet Server Performance, ACM Press, 1999.
  14. O. Ardaiz, F. Freitag and L. Navarro, “Improving Service Time of Web Clients Using Server Redirection,” ACM SIGMETRICS Performances Evaluation Review, Vol. 29, No. 2, 2001, pp. 39-44. doi:10.1145/572317.572324
  15. S. Kalepu, S. Krishnaswamy and S. W. Loke, “Verity: A QoS Metric for Selecting Web Services and Providers,” Proceedings of the 4th International Conference on Web Mining System Engineering Workshops (WISEW’03), 2004, pp. 131-139. doi:10.1109/WISEW.2003.1286795
  16. S. Araban and L. Sterling, “Measuring Quality of Service for Contract Aware Web-Services,” First Australian Work- shop on Engineering Service-Oriented Systems (AWESOS 2004), Melbourne, 29 January 2004, pp. 116-127.
  17. QWS Datasets. http://www.uogue/ph.ca/~qmahmoud/qws/index.html
  18. E. AL-Masri and Q. H. Mahmoud, “Investing Web Services on the World Wide Web,” The 17th International Conference on World Wide Web, Beijing, 21-25 April 2008, pp. 795-804.
  19. E. AL-Masri and Q. H. Mahmoud, “QoS Based Discovery and Ranking of Web Services,” IEEE 16th International Conference on Computer Communications and Networks (ICCCN), Honolulu, 13-16 August 2007, pp. 529-534. doi:10.1109/ICCCN.2007.4317873
  20. J. Pearl, “Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference,” Morgan Kaufmann, 1988.
  21. F. Glover and M. Laguna, “Tabu Search,” Kluwer Academic Publishers, Amsterdam, 1997. doi:10.1007/978-1-4615-6089-0
  22. R. Mohanty, V. Ravi and M. R. Patra, “Web Services Classification Using Intelligent Techniques,” Expert Systems with Applications, Vol. 37, No. 7, 2010, pp. 5484- 5490. doi:10.1016/j.eswa.2010.02.063

NOTES

*Corresponding author.

Journal Menu >>