ABSTRACT

This article presents a new signcryption scheme which is based on the Schnorr digital signature algorithm. The new scheme represents my personal contribution to signcryption area. I have implemented the algorithm in a program and here are provided the steps of the algorithm, the results and some examples. The paper also contains the presentation of the original Signcryption scheme, based on ElGamal digital signature and discusses the practical applications of Signcryption in real life. The purpose of the study is to combine the public key encryption with Schnorr digital signature in order to obtain less computational and communicational costs. Signcryption primitive is a better approach then Encrypt-thenSign or Sign-then-Encrypt methods regarding the costs. All these algorithms offer the possibility to transmit a message over an insecure channel providing both authenticity and confidentiality.

1. Introduction

Signcryption is the primitive that has been proposed by Youliang Zheng in 1997 and combines public key encryption with digital signature in a single logical step, obtaining a less cost for both communication and computation [1].

Data confidentiality and data integrity are two of the most important functions of modern cryptography. Confidentiality can be achieved using encryption algorithms or ciphers, whereas integrity can be provided by the use of authentication techniques. Encryption algorithms fall into one of two broad groups: private key encryption and public key encryption. Likewise, authentication techniques can be categorized by private key authentication algorithms and public key digital signatures.

While both private key encryption and private key authentication admit very fast computation with minimal message expansion, public key encryption and digital signatures generally require heavy computation, such as exponentiations involving very large integers, together with message expansion proportional to security parameters (such as the size of a large composite integer or the size of a large finite field).

Signcryption has the intention that the primitive should satisfy “Cost (Signature & Encryption) Cost (Signature) + Cost (Encryption)” This inequality can be interpreted in a number of ways:

• A signcryption scheme should be more computationnally efficient than a native combination of public-key encryption and digital signatures.

• A signcryption scheme should produce a signcryption “ciphertext” which is shorter than a naive combination of a public-key encryption ciphertext and a digital signature.

• A signcryption scheme should provide greater security guarantees and/or greater functionality than a native combination of public-key encryption and digital signatures [1].

More recently, the significance of signcryption in realworld applications has gained recognition by experts in data security. Since 2007, a technical committee within the International Organization for Standardization (ISO/IEC JTC 1/SC 27) has been developing an international standard for signcryption techniques [2].

The shared secret key between the parties makes possible an unlimited number of applications. Among these applications, one can first think of the following three:

• Secure and authenticated key establishment,

• Secure multicasting, and

• Authenticated key recovery.

A number of signcryption-based security protocols have been proposed for aforementioned networks and similar environments. These include:

• Secure ATM networks

• Secure routing in mobile ad hoc networks

• Secure voice over IP (VoIP) solutions

• Encrypted email authentication by firewalls

• Secure message transmission by proxy, and

• Secure message transmission by proxy, and

• Mobile grid web services.

There are also various applications of signcryption in electronic commerce, where its security properties are very useful. Analyzing this security scheme from an application-oriented point of view, can be observed that a great amount of electronic commerce can take advantage of signcryption to provide efficient security solutions in the following areas:

• Electronic payment

• Electronic toll collection system

• Authenticated and secured transactions with smart cards, etc.

My personal contribution to the article is represented by the Schnorr Signcryption scheme which has been introduced here. Schnorr Signcryption scheme is made up of a combination between a public key encryption scheme and a digital signature scheme. On the base of the scheme that I present here stands the Schnorr digital signature. A Schnorr signature is a digital signature produced by the Schnorr signature algorithm. Its security is based on the intractability of certain discrete logarithm problems. It is considered the simplest digital signature scheme to be provably secure in a random oracle model. It is efficient and generates short signatures.

A signcryption scheme typically consists of five algorithms, Setup, KeyGenS, KeyGenR, Signcrypt, Unsigncrypt:

• Setup-takes as input a security parameter 1^ k and outputs any common parameters param required by the signcryption schemes. This may include the security parameter 1^ k, the description of a group G and a generator g for that group, choices for hash functions or symmetric encryption schemes, etc.

• Key Generation S(Gen) generates a pair of keys for the sender.

• Key Generation R(Gen) generates a pair of keys for the receiver.

• Signcryption (SC) is a probabilistic algorithm.

• Unsigncryption (USC) is a deterministic algorithm.

A signcryption scheme is a combination between a public key encryption algorithm and a digital signature scheme.

A public key encryption scheme consists of three polynomial-time algorithms (EncKeyGen, Encrypt, Decrypt).

EncKeyGen—Key generation is a probabilistic algorithm that takes as input a security parameter 1^ k and outputs a key pair (skenc, pkenc), written (skenc, pkenc)R←EncKeyGen (1^ k ). The public encryption key pkenc is widely distributed, while the private decryption key skebnc should be kept secret. The public key defines a message m ∈ M and a ciphertext ∈ C.

Encrypt—Encryption is a probabilistic algorithm that takes a message m ∈ M and the public key pkenc as input and outputs a ciphertext C ∈ C, written C ← Encrypt (pkenc, m).

Decrypt—Decryption is a deterministic algorithm that takes a ciphertext C ∈ C and the private key skenc as input and outputs either a message m ∈ M or the failure symbol ⊥, written m ← Decrypt (skenc, C).

The article is structured in seven parts, as follows. Signcryption and its properties definitions are contained in the first part. Also here, in introduction, are presented the practical applications of Signcryption in real life. In the second part is exposed the original signcryption primitive introduced by Youliang Zheng, which combines public key encryption and a derivation of ElGamal digital signature algorithm. Part three contains the presentation of the new sygncryption scheme, Schnorr Signcryption, as a result of the combination of public key encryption and Schnorr digital signature algorithm. The step-by-step implementtation of the Schnorr Signcryption scheme in a source code program is reflected in the fourth part. Strating with the fifth part begins the analyze of the security models on Schnorr Signcryption. The two-users security model is presented in the sixth part and multi-user security model is presented in the seventh part. In each of this models there is exposed another classification for security, the insider security and the outsider security.

2. Related Work

2.1. Elgamal Signcryption

The original signcryption scheme that has been introduced by Youliang Zheng in 1997 is created on a derivation of ElGamal digital signature standard, combined with a public key encryption scheme.

Based on discrete algorithm problem, ElGamal Signcryption cost is:

58% less in average computation time;

70% less in message expansion.

Here is the detailed presentation of the fifth algorithms that make up the ElGamal signcryption scheme.

1) Setup Signcryption parameters:

p = a large prime number, public to all;

q = a large prime factor of p − 1, public to all;

g = an integer with order q modulo p, in [1, , p − 1], public to all;

hash = a one-way hash function;

KH = a keyed one-way hash function = KHk(m) = hash (k, m);

(E, D) = the algorithms which are used for encryption and decryption of a private key cipher.

Alice sends a message to Bob.

2) KeyGen sender Alice has the pair of keys (Xa, Ya):

Xa = Alice’s private key, chosen randomly from [1, , q − 1]

Ya = Alice’s public key = mod p.

3) KeyGen receiver Bob has the pair of keys (Xb, Yb):

Xb = Bob’s private key, chosen randomly from [1, , q − 1]

Yb = Bob’s public key =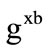 mod p.

4) Signcryption In order to signcrypt a message m to Bob, Alice has to accomplish the following operations:

Calculate

Split k in k1 and k2 of appropriate length.

Calculate r = KHk2(m) = hash(k2, m)

Calculate s = x/(r + Xa) mod q, if SDSS1 is used Calculate s = x/(1 + Xa ∙ r) mod q, if SDSS2 is used Calculate c = Ek1(m) = the encryption of the message m with the key k1.

Alice sends to Bob the values (r, s, c).

5) Unsigncryption In order to unsigncrypt a message from Alice, Bob has to accomplish the following operations:

Calculate k using r, s, g, p, Ya and Xb

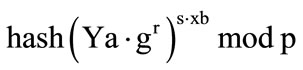, if is used SDSS1;

, if is used SDSS2;

Split k in k1 and k2 of appropriate length.

Calculate m using the decryption algorithm m = Dk1(c).

Accept m as a valid message only if KHk2(m) = r.

Using the two schemes SDSS1 and SDSS2, two signcryption schemes have been created, SCS1 and SCS2, respectively. The two signcryption schemes share the same communication overhead, (|hash(*)| + |q|). SCS1 involves one less modular multiplication in signcryption then SCS2, both have a similar computational cost for unsigncryption [1].

2.2. Rsa Signcryption

Rivest introduced for the first time in 1978 the publickey encryption scheme and digital signature scheme [3].

The RSA transform has been the basis of dozens of public-key encryption schemes and digital signature schemes, which have proven to be very successful and have been very widely deployed in industry. They are widely used in the design of public-key encryption and digital signature schemes.

The RSA transform was introduced by Rivest, Shamir, and Adleman in 1978 [3]. The exact definition of the problem depends upon the distribution from which the two prime numbers p and q are drawn. For our purposes, this is defined by a probabilistic, polynomial-time RSA parameter generation algorithm RSAGen, which takes as input a security parameter 1^ k and outputs two primes (p, q) with the property that N = pq is a k-bit integer [4].

Signcrypt ()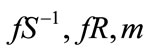

Bind ßpkS||pkR r ß

c ß H (bind, m||r)

d ß m||r w ß c s ß G (bind, c) ○ d C ß fR (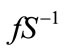 (w||s))

Return C Unsigncrypt ()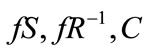

Bind ß pkS||pkR

(w||s) ß fS ()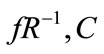

m||r ß G (bind, w) © s If H (bind, m||r) = w, return m Else return ⊥

2.3. Elliptic Curve Cryptography Signcryption

The first signcryption scheme was introduced by Yuliang Zheng in 1997 [1]. Zheng also proposed an elliptic curvebased signcryption scheme that saves 58% of computational and 40% of communication costs when it is compared with the traditional elliptic curve-based signaturethen-encryption schemes [5].

Here is presented the scheme for an elliptic curve based signcryption algorithm introduced by Mohsen Toorani and Ali Asghar Beheshti Shirazi in [6].

Signcryption (Alice)

Choosing r in [1, n − 1]

R = rG = (xR, yR)

K = rU = (xK, yK)

s =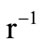 (H (M) + xRdA) (mod n)

e = H (M||s)

C = (M||e) © xK

Unsigncryption (Bob)

K = dB R = (xK, yK)

(M||e’) = C © xK e’ = H(M||s)

If e <> e’ then rejects M’

Else u =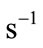H(M)

v =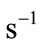xR uG + vU = (x’R, y’R)

Signature verification: Is xR = x’R ?

The elliptic curve-based schemes are usually based on difficulty of Elliptic Curve Discrete Logarithm Problem (ECDLP) that is computationally infeasible under certain circumstances [7]. The elliptic curve-based systems can attain to a desired security level with significantly smaller keys than those of required by their exponential-based counterparts. This can enhance the speed and leads to efficient use of power, bandwidth, and storage that are the basic limitations of resource-constrained devices [8].

Throughout the years, there have been proposed many other signcryption schemes, each with its own problems and limitations, while offering different level of security services and computational costs.

3. Implementation of the New Signcryption Scheme

A Schnorr signature is a digital signature produced by the Schnorr signature algorithm. Its security is based on the intractability of certain discrete logarithm problems. It is considered the simplest digital signature scheme to be provably secure in a random oracle model [9].

Choosing parameters

All users of the signature scheme agree on a group G with generator g of prime order q in which the discrete log problem is hard.

Key generation

Choose a private signing key x.

The public verification key is y = g^x.

Signing

To sign a message M:

Choose a random k.

Let r = g^k

Let e = H (M | | r), where || denotes concatenation and r is represented as a bit string. H is a cryptographic hash function.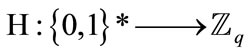

Let s = (k – xe).

The signature is the pair (s, e).

Verifying

Let r_v = g^sy^e

Let e_v = H (M | | r_v)

If e_v = e then the signature is verified.

Demonstration of correctness

It can be observed that e_v = e if the signed message equals the verified message:

, and hence e_v = H (M | | r_v) = H(M | | r) = e.

It has been considered that k < q and the assumption that the hash function is collision-resistant.

Public elements: G, g, q, y, s, e, r.

Private elements: k, x. [10]

A Schnorr Signcryption scheme is based on Schnorr digital signature algorithm.

Here is the detailed presentation of the fifth algorithms that make up the Schnorr signcryption scheme.

1) Setup Schnorr Signcryption parameters:

p = a large prime number, public to all;

q = a large prime factor of p-1, public to all;

g = an integer with order q modulo p, in [1, , p − 1], public to all;

hash = a one-way hash function;

KH = a keyed one-way hash function = KHk (m) = hash (k, m);

(E, D) = the algorithms which are used for encryption and decryption of a private key cipher.

Alice sends a message to Bob.

2) KeyGen sender Alice has the pair of keys (Xa, Ya):

Xa = Alice’s private key, chosen randomly from [1, , q − 1]

Ya = Alice’s public key = 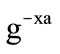mod p.

3) KeyGen receiver Bob has the pair of keys (Xb, Yb):

Xb = Bob’s private key, chosen randomly from [1, , q − 1];

Yb = Bob’s public key = mod p.

4) Signcryption In order to signcrypt a message m to Bob, Alice has to accomplish the following operations:

Calculate

;

Split k in k1 and k2 of appropriate length.

Calculate r = KHk2(m) = hash (h2, m);

Calculate s = x + (r* Xa) mod q;

Calculate c = Ek1(m) = the encryption of the message m with the key k1.

Alice sends to Bob the values (r, s, c).

5) Unsigncryption In order to unsigncrypt a message from Alice, Bob has to accomplish the following operations:

Calculate k using r, s, g, p, Ya and Xb

Split k in k1 and k2 of appropriate length.

Calculate m using the decryption algorithm m = Dk1 (c).

Accept m as a valid message only if KHk2 (m) = r.

Analyzing the two presented signcryption schemes, it can be observed that in case of Shnorr signcryption the computation of s, which is s = x + (r* Xa) mod q, is less consuming comparing with the formula used in ElGamal algorithm, where s is s = x/(r+Xa) mod q.

Another difference is on the level of unsigncryption step as k is computing differently, using this formula for Schrr and this formula for Elmal.

4. Security Models for Schnorr Signcryption Scheme

The first attempt to produce security models for signcrtion was given by Steinfeld and Zheng [11].

A family of security models for signcryption in both two-user and multi-user settings was presented by An [12] in their work on signcryption schemes built from blackbox signature and encryption schemes.

Defining the security of signcryption in the public-key setting is more involved than the corresponding task in the symmetric setting [13] due to the asymmetric nature of the former. The asymmetry of keys makes a difference in the notions of both authenticity and privacy on two major fronts which are addressed in this chapter.

The first difference for Schnorr signcryption is that the security of the signcryption needs to be defined in the multi-user setting, where issues with users’ identities need to be addressed. On the other hand, authenticated encryption in the symmetric setting can be fully defined in a much simpler two-user setting.

The case of Schnorr settings not only makes a difference in the multiuser and two-user settings but also makes a difference in the adversary’s position depending on its knowledge of the keys. There are two definitions for security of signcryption depending on whether the adversary is an “outsider” (a third party who only knows the public information) or “insider” (a legal user of the network, either the sender or the receiver, or someone that knows the secret key of either the sender or the receiver). In the first case the security model is named “outsider security” and in the latter “insider security”.

4.1. Two-Users Security Model

In the symmetric setting, there is only one specific pair of users who 1) Share a single key;

2) Trust each other;

3) “Know who they are”;

4) Only care about being protected from “the rest of the world.”

In contrast, in Schnorr signcryption setting, each user independently publishes its public keys, after which it can send/receive messages to/from any other user. In particular, 1) each user should have an explicit identity (associated with its public key); 2) each signcryption has to explicitly contain the (presumed) identities of the sender S and the receiver R; 3) each user should be protected from every other user.

The security goal is to provide both authenticity and privacy of communicated data. In the symmetric setting, since the sender and the receiver share the same secret key, the only security model that makes sense is one in which the adversary is modeled as a third party or an outsider who does not know the shared secret key. For Schnorr signcryption setting, the sender and the receiver do not share the same secret key but each has his/her own secret key. Due to this asymmetry of the secret keys, the data needs to be protected not only from an outsider but also from an insider who is a legal user of the system (the sender or the receiver themselves or someone who knows either the sender’s secret key or the receiver’s secret key) [4].

4.2. Multi-User Security Model

A central difference between the multi-user model and the two-user models is the extra power of the adversary. In the multi-user model, the attacker may choose receiver (resp. sender) public keys when accessing the attacked users’ signcryption (resp. unsigncryption) oracles. For signcryption schemes that share some functionality between the signature and the encryption components, such as are the case for Zheng’s Signcryption scheme and Schnorr Signcryption scheme, the extra power of the adversary in the multi-user model may be much more significant, and a careful case-by-case analysis is required to establish security of such schemes in the multi-user model.

As in the two-user setting, the multi-user setting also has two types of models depending on the identity of the attacker: an insider model and an outsider model.

5. Experimental Results

Here is provided an example from the execution of the program on small numbers.

Example:

p = 23, q = 11, g = 2, X=3 XA = 4 => YA=13 XB=5 => YB=18 k = 13 => hash(k) = vTB6PsMp4Qos/4+4dICCPaEU+ PQ=

k1 = vTB6PsMp4Qos/w==

k2 = j7h0gII9oRT49A==

hash(k2, m) = E2726583242AB5CCE58AE1151DB126208F17932F hash(k2, m) in base 10 = 1292783042124763369608714420962730428414981280- 559

(hash(k2,m) in base 10) mod p = 3 s mod q = x + (r*Xa) mod q = 4 Unsigncrypt k = 13 In Table 1 is presented the cost evaluation for the signature and verification in ElGamal and Schnorr signcryption schemes.

It is important the improvement for the cost consumption that has been made in the case of the proposed scheme, as at this step it is not necessary to be calculated the modular inverse.

• Texp: the time for a modular exponential computation.

• Tm: the time for a modular multiplication computation.

• Tinv: the time for a modular inverse computation.

• Th: the time for a one way hash function f(_) computation.

6. Conclusions and Future Work

This paper presents a new Signcryption scheme which is

based on Schnorr digital signature algorithm. This scheme is named Schnorr Signcryption and it implements in a single logical step both public key encryption and digital signature, offering less costs as using these two cryptographic functions individually.

In signcryption area, the following problems seem interesting in future research: 1) presenting a formal model for group signcryption, and proposing provably secure schemes; 2) Designing schemes to support dynamic group member management in the sense that group member can join or leave the group efficiently and dynamically; 3) Optimizing the open procedure so that it does not linearly depend on the number of group members, so that such schemes are suitable for large groups.

REFERENCES

Appendix

I created a source code program that verifies my algorithm. Executing this program I could generate examples. The step-by-step implementation of the algorithm is as follows:

1) Calculate Ya and Yb double powA = Math.Pow(g, xA);

int pow_intA = Convert.ToInt32(powA);

int invA = modInverse(pow_intA, p);

2) Calculate k int yB = Convert.ToInt32(textBox11.Text);

int x = Convert.ToInt32(textBox18.Text);

int p = Convert.ToInt32(textBox4.Text);

string cheie = (BigInteger.ModPow(yB, x, p)). ToString();

3) Calculate hash(k)

string HashDeCheie = _calculateHash(cheie);

textBox13.Text = HashDeCheie;

4) Split k in two keys k1 and k2 with the same lenght byte[] k = Convert.FromBase64String(textBox13.Text);

byte[] k1 = new byte[k.Length/2];

byte[] k2 = new byte[k.Length - k.Length/2];

Buffer.BlockCopy(k, 0, k1, 0, k.Length/2);

Buffer.BlockCopy(k, k.Length/2, k2, 0, k.Length - k.Length/2);

byte[] test = new byte[k.Length];

k1.CopyTo(test, 0);

k2.CopyTo(test, k1.Length);

5) Calculate r using k2; r = hash (k2, m)

BigInteger p = BigInteger.Parse(textBox4.Text);

System.Text.ASCIIEncoding encoding = new System.Text.ASCIIEncoding();

byte[] keyByte = encoding.GetBytes(key);

HMACSHA1 hmacsha1 = new HMACSHA1(keyByte);

byte[] messageBytes =encoding.GetBytes(message);

byte[] hashmessage = hmacsha1.ComputeHash(messageBytes);

6) Calculate r using k2; transform the value obtained from hash in base 10 textBox19.Text = fn16to10(textBox15.Text).ToIntString();

7) Calculate the modulo p of the number obtained in base 10 BigInteger nr = BigInteger.Parse(textBox19.Text);

BigInteger p = BigInteger.Parse(textBox4.Text);

BigInteger rest = 0;

BigInteger.DivRem(nr, p, out rest);

8) Calculate s BigInteger q = Convert.ToInt32(textBox5.Text);

BigInteger  r = Convert.ToInt32(textBox20.Text);

BigInteger XA = Convert.ToInt32(textBox9.Text);

BigInteger X = Convert.ToInt32(textBox18.Text);

BigInteger prod = BigInteger.Multiply(r, XA);

BigInteger sum = X + prod;

BigInteger rest;

BigInteger.DivRem(sum, q, out rest);

9) Encrypt m using the k1 10) Calculate k BigInteger rez2 = BigInteger.Pow(rez1, XB);

BigInteger invK = modInverseBI(rez2, p)