Journal of Biomedical Science and Engineering
Vol.7 No.4(2014), Article ID:43967,5 pages DOI:10.4236/jbise.2014.74026
A Contact Model for Establishment of Hip Joint Implant Wear Metrics
Mohammad Hodaei, Kambiz Farhang, Nazanin Maani
Department of Mechanical Engineering and Energy Processes, Southern Illinois University, Carbondale, USA
Email: mhodaei@siu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 12 January 2014; revised 17 February 2014; accepted 25 February 2014
ABSTRACT
Wear is an important issue in hip implants. Excessive wear can lead to toxicity and other implant associated medical issues such as patient discomfort and decreased mobility. Since implant wear is the result of contact between surfaces of femoral head and acetabulum implant, it is important to establish a model that can address implant surface roughness interaction. A statistical contact model is developed for the interaction of femoral head and acetabulum implant in which surface roughness effects are included. The model accounts for the elastic-plastic interaction of the implant surface roughness. For this purpose femoral head and acetabulum implants are considered as macroscopically spherical surfaces containing micron-scale roughness. Approximate equations are obtained that relate the contact force to the mean surface separation explicitly. Closed form equations are obtained for hysteretic energy loss in implant using the approximate equations.
Keywords:Contact Mechanics; Roughness; Hip Implant; Wear; Energy Loss; Toxicity

1. Introduction
Hip joint serves as one of the most important load bearing joints in human body. Studies have shown that up to 5.5 times the bodyweight is tolerated by femur and pelvis during daily activities [1] -[3] . These include normal activities such as walking, going up or down a set of stairs, getting up or sitting down, carrying groceries or other loads. A hip joint provides, in addition to its load bearing ability, the needed mobility that includes extension, rotation, and flexion. Most importantly, hip joints provide smooth articulation of limbs necessary for bi-pedal gait.
Hip joint malfunction may occur as a result of many factors. The most prevalent cause of hip joint surgical operation and hip joint replacement is osteoarthritis (OA). OA occurs when the cartilage fissuring is severe enough to a point where bone contact is initiated at the hip joint. OA is attributed to many causes [1] that include age, overuse, excessive loading, or flaw in the hip joint geometry referred to hip dysplasia. It is estimated that about 200,000 hip replacements occur in the United States due to hip joint OA. Other hip joint problems include osteolysis, avascular necrosis, neck fracture of femur [4] -[6] . The purpose of the present paper is not to address the causes of hip replacement, but it is to address the performance of a hip joint after surgery.
Hip joint implant is designed to provide the same mobility and stability of the original functioning hip joint. Certainly, the design of hip joint implant needs to investigate all parameters such as wear, roughness, erosion, tribology, materials, and also many problems caused by surgical procedure including bone replacement. Some of these factors have been studied since about 50 years ago. About 50 years ago, McLaurin [7] investigated the manufacturing of hip prostheses. At that time, the design encountered wear problems because of metal on metal contact. Smith and Nephew [8] made an experimental model of hip joint using oxidized zirconium alloy technology in femoral head of hip joint to reduce wear and improve longevity in comparison with using ceramics for femoral head. In the last two decades, advances in imaging technology have allowed better preoperative data generation and improved preparation and planning of surgery [9] -[12] . A more recent work by Shapi et al. [13] allows preoperative measurement of the size of acetabular implant in total hip replacement.
Hiroyuki et al. [14] evaluated the effect of RF heating on hip joint implant during MRI examinations. They used two types of different implants in material and shapes. They found that the electrical characteristics of metallic implants have influence on RF heating. Maximum temperature was found to occur at the tip of the implants, location of large curvature. Zhang et al. [15] compared stress distributions between silicon nitride and cobalt-chromium-alloy in hip prostheses. The results related to stress distributions with the implanted silicon nitride hip resurfacing prostheses are very close to the corresponding stresses for health, intact femur bone. Scifert et al. [16] developed a new design to reduce the tendency of dislocation in Hip implants in patients. The authors claim that their proposed design increases stability of total hip joint and decreases by fifty percent stress distributions around impingement zone of polyethylene. Phillips et al. [17] used an elasto-plastic material model to show constitutive behavior of morsellised cortico-cancellous bone graft. Three 3D load scenarios related to walking, sitting, and standing were applied at the center of femoral head to check migration and rotation of the acetabular cup. Walking causes superior migration and rotation in abduction of the acetabular cup while sitting down and standing up causes posterior migration and rotation of the acetabular cup. Jonathon et al. [18] investigated dangerous effects of metal release from hip prostheses on patients.
Metal-on-metal hip prostheses failed in some patients due to the release of metal debris resulting in revision surgery. Symptoms such as neurological impairment, cardiomyopathy, and hypothyroidism were reported in their study. Steens et al. [19] showed that the effect of ceramic-onceramic toxicity in the blood can lead to impairment of hearing, sight, numbness in feet, and dermatitis in head and neck. Tower [20] also showed the dangerous effects of metal debris in human blood pain such as onset of anxiety, major depression, tinnitus, high frequency hearing loss, peripheral neuropathy, and cognitive decline. Alan and Swarts [21] investigated the effect of modularity on tapered cone of Margron hip prosthesis. Their study found that increased modularity can cause corrosion and crack, debris of particles, and metal ion generation. Brodner et al. [22] investigated the levels of serum cobalt in patients before and after implantation of non-cemented total hip arthroplasties. As a result, they show that the metal-on-metal prostheses produce detectable levels of serum cobalt in comparison with the ceramic-polyethylene prostheses as metal-on-metal prostheses generate some systemic release of cobalt. Many more publications exist in the literature on hip implant. These can be categorized as those advocating the use of cemented joints for attachment of hip implant for reliable bonding with bone [23] -[34] . A number of papers delve into the experimental investigation of hip implants, whereas others present numerical simulation of hip joint implant using the finite element models [35] -[37] .
To address the issues related to wear and thereby potential toxicity effects of an implant, it is important to have a mathematical tool to predict the effect of implant surface finish. The use of FEM is impractical in this case since such an effort would involve a prohibitively large number of elements amounting to more than one million elements for a mere one square millimeter nominal area. This paper develops a statistically-based contact mechanics model of hip joint taking into account the effect of the surface roughness geometry of the implant. An elastic-plastic model of the spheres in contact representing the femoral and acetabular implants is developed.
The specific contribution of this paper includes: (1) inclusion of implant surface roughness in hip implant contact model, (2) approximate equations relating the contact force to minimum mean plane separation in an explicit form, (3) energy loss per load-unload cycle that includes macro and micro geometry of the implant surfaces, and (4) characterization of hip implant natural contact frequency and contact damping The results agree with the recent issues with hip implant failures when metal-on-metal is employed. The model presented is, therefore, a necessary first step in the prediction of possible wear in hip implants and issues related to wear borne toxicity in implant recipients.
Template, created in MS Word 2003 and saved as “Word 97-2003 & 6.0/95-RTF” for the PC, provides authors with most of the formatting specifications needed for preparing electronic versions of their papers. All standard paper components have been specified for three reasons: 1) ease of use when formatting individual papers, 2) automatic compliance to electronic requirements that facilitate the concurrent or later production of electronic products, and 3) conformity of style throughout a journal paper. Margins, column widths, line spacing, and type styles are built-in; examples of the type styles are provided throughout this document and are identified in italic type, within parentheses, following the example. Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.
2. Hip Contact Model
The schematic diagram of a hip joint is shown in Figure 1. Figure 1 shows that force transfer to hip gives rise to contact force between the femoral head and acétabulés, whose shapes are approximated using spheres. Let R1 and R2 be the radii of curvature of the femoral head and acetabulum, respectively. Figure 2 details the contact between two spheres of radii R1 and R2. When roughness of the surfaces is incorporated into the contact model, it is expected that the load-carrying zone be defined by a minimum separation with symmetrically distributed pressure about the minimum separation. Since the number of contact points and their respective pressure depend on the mean surface separation of the two spheres, it is necessary to develop the expression for mean separation as a function of minimum separation and the geometries of the two spheres. In contact of femoral head with acetabulum, we confront a conformal contact. This is represented by the sphere contact in Figure 1. The schematic drawing of the mean spheres of the femoral head and the acetabulum surface in Figure 2 shows that for a mean surface separation h0, the offset between sphere centers, δ, can be expressed in terms of h0.
 (1)
(1)
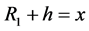 (2)
(2)
where, the triangle shown in Figure 2, clearly shows that the mean plane separation, h, can be found in terms of minimum separation, h0, radii of the two spheres, R1 and R2, and the angular location measured with respect to the inner (smaller) sphere.
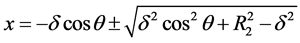 (3)
(3)
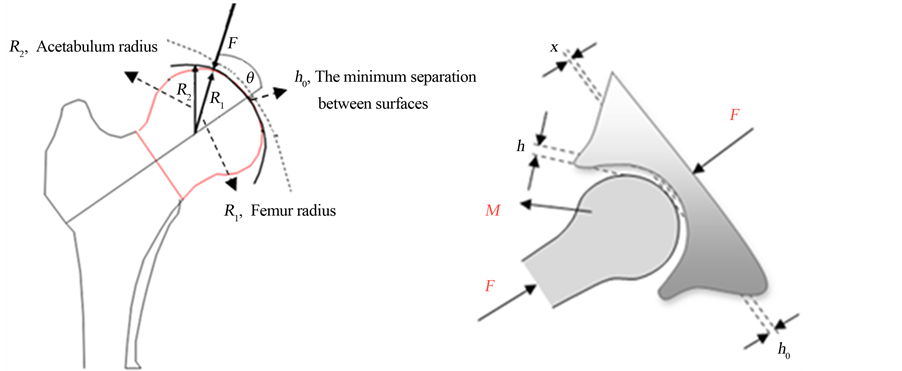
Figure 1. Schematic depiction of hip joint.
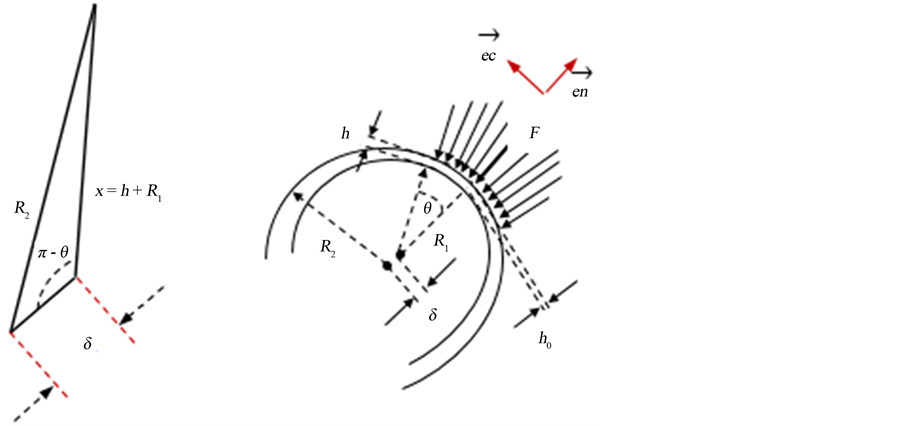
Figure 2. Spheres in internal contact.
An acceptable solution in Equation (3) must yield a positive x. Therefore,
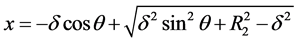 (4)
(4)
Substitute for x in terms of R1 and h and solve the resulting equation for h, the separation at location θ. We find from Equations (2) and (4),
 (5)
(5)
Substitute for δ from Equation (1) to find
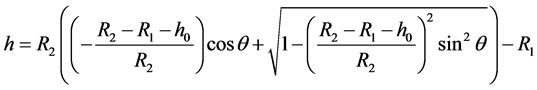 (6)
(6)
Since the mean surface separation is defined, we can proceed to derive the contact force per unit nominal area due to elastic-plastic interaction of the roughness of the femoral and acetabulum surfaces. The contact force per unit nominal area can be expressed as follows [23] ,
 (7)
(7)
where, Pe(h) is the elastic force per unit nominal area given by the following Equation, [38]
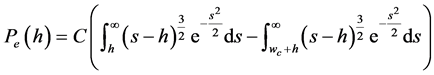 (8)
(8)
where,
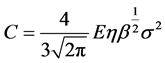 (9)
(9)
s and h are both dimensionless. s is the ratio of an asperity height over the standard deviation of asperity summit distribution, σ, and h is the ratio of the mean surface separation over σ. When the surfaces are pressed together, there may be locations within the contact zone where asperity interference results in onset of plastic deformation. Greenwood and Williamson [39] defines asperity critical interference to be the onset of plastic deformation. In following the CEB model [40] , the authors employed the definition of the critical interference to formulate the elastic-plastic model of contact. In Equation (8) wc represents the dimensionless critical interference. Greenwood and Williamson [39] defines plasticity index for a surface as follows:
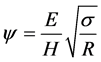
where, R is the average asperity summit radius of curvature, E is the equivalent modulus and H is the hardness of the softer material. They also define critical interference as
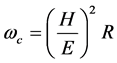
Letting  be the dimensionless critical interference, the plasticity index,
be the dimensionless critical interference, the plasticity index,![]() , is related to the wc as follows
, is related to the wc as follows
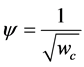 (10)
(10)
Equation (8) uses a constant C and the dimensionless force expression in integral form for the elastic part of the surface interaction. C is defined as given by Equation (9), in which E is the reduced modulus of elasticity of the two surfaces, b is the dimensionless equivalent average asperity radius of curvature. The reduced modulus of elasticity is derived from the properties of the material used in the implant. It is given by the following equation
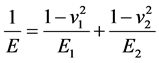 (11)
(11)
where, E1 and  are the modulus of elasticity and Poisson ratio of the femoral implant material and E2 and
are the modulus of elasticity and Poisson ratio of the femoral implant material and E2 and 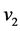 are those of the acetabulum implant. The equivalent asperity radius is found using
are those of the acetabulum implant. The equivalent asperity radius is found using
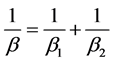 (12)
(12)
where, ![]() and
and  are the average asperity radius of curvature of the femoral and acetabulum implants, respectively. h is the asperity density per unit area. The force per unit normal area due to plastic interaction in an elastic-plastic contact is [40] .
are the average asperity radius of curvature of the femoral and acetabulum implants, respectively. h is the asperity density per unit area. The force per unit normal area due to plastic interaction in an elastic-plastic contact is [40] .
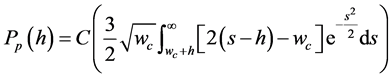 (13)
(13)
To obtain the contact force along a particular direction, one must sum the force components along that direction due to infinitesimal contact forces that occur over an infinitesimal area. Sum of the contact infinitesimal contact forces along the line of symmetry will be result in the total contact force, whereas those along the normal to the line symmetry vanish. Sum the force components parallel to the radial line of symmetry with respect to the nominal contact area to find
 (14)
(14)
where, R is the equivalent macro radius of curvature of the spheres representing femoral and acetabulum implants
 (15)
(15)
The integral in Equation (14) can be reduced to the following
 (16)
(16)
It will prove beneficial to express Equation (16) as an explicit function of the minimum separation, h0. Since h is a function of integration variable Ɵ, Equation (6), the integral in Equation (6) can only be found numerically. As a result, we set out to find an approximate relation between contact force F and the minimum separation h0. It will be shown in the next section that the contact force may be estimated using a function of the form 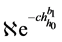 .
.
2.1. Dependence of Coefficients on Hip Radii
In this section acetabulum and femoral radii are used as parameters in the approximate expression relating contact force to minimum mean surface separation. It can be shown that the approximate equation is of the following form
 (17)
(17)
The values are generated for various femoral head radii, ranging from 5 mm to 25 mm. Where, the coefficients ℵ and c are expected to depend on the geometry of the hip and the plasticity index.
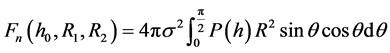 (18)
(18)
In obtaining the approximate equation, the femoral radius is varied, and the acetabulum radius is assumed to be 0.2 mm larger than the femoral radius. Femoral radius is varied from 5 mm to 25 mm [26] while in each case acetabulum radius is kept 0.2 mm larger. For a purely elastic contact this results in c = 1.99 and
![]() (19)
(19)
where,
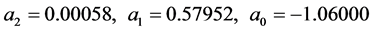 (20)
(20)
The maximum error between fitted and original function for purely elastic contact is less than 5% over the entire range of parameters considered.
2.2. Dependence of Coefficients on Plasticity Index ψ
In this section, approximate functional relationships between the coefficients and plasticity index are established for plasticity index ranging 0.3 to 1.3. Keep in mind that for surfaces characterized by ψ < 0.6 the surface is considered predominantly elastic, while for 0.6 < ψ < 1 the surface is viewed as elastic-plastic.
![]() (21)
(21)
![]() (22)
(22)
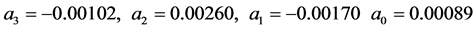 (23)
(23)
Likewise, the fitted function for b is
![]() (24)
(24)
with coefficients
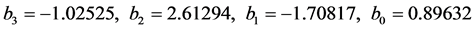 (25)
(25)
The function c(ψ) is defined as follows
![]() (26)
(26)
where,
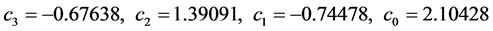 (27)
(27)
Finally, plasticity function with low percent error for a, b, and c is
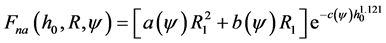 (28)
(28)
Figure 3 shows that the max error between the approximate and original elastic-plastic contact force is less
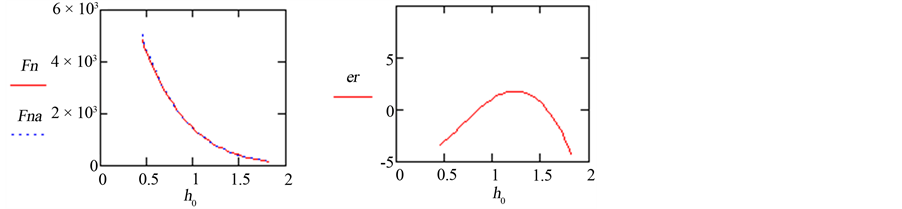
Figure 3. Approximation of normal force and associated percent error.
than 5% over the entire range of parameters considered.
2.3. Energy Loss in Hip Implant
The contact between femoral and acetabulum implant surfaces consists of asperities experiencing elastic and plastic deformation. A close look at the loading and unloading process reveals that both energy loss and elastic recovery are involved in the process. During the increase in contact load both elastic and plastic deformations can occur at asperity deformation level. However, during unloading asperities undergo only elastic recovery. Therefore, the load and unload process will follow different paths, resulting in hysteresis type energy loss in the hip joint contact.
We can employ the approximate equations for elastic-plastic contact and purely elastic contact to represent the loading and unloading process mathematically. The force during loading is denoted 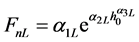 and that during unloading,
and that during unloading, 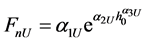 . Based on the results of the previous section, the respective coefficients of contact force during load and unload are as follows:
. Based on the results of the previous section, the respective coefficients of contact force during load and unload are as follows:
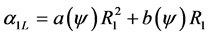 (29)
(29)
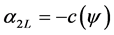 (30)
(30)
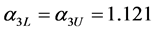 (31)
(31)
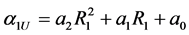 (32)
(32)
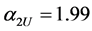 (33)
(33)
To study energy loss and storage in a hip joint, we consider an equilibrium contact force. For example this may correspond to an individual standing still and a contact force equal to the equilibrium force exists between femoral head and acetabulum. The equilibrium contact force is associated with an equilibrium minimum mean plane separation, h0. A disturbance from equilibrium is denoted x. Therefore, to study the behavior of the contact near an equilibrium state, we can use the contact force equations above. Depending on the nature of the disturbance, the load may increase from equilibrium or decrease from it. If the load is increasing from equilibrium then both elastic and plastic contacts must be included in the calculation of contact force. If the load is decreasing from the equilibrium state, then only elastic contacts contribute, since this is a load recovery process. The following expressions will be adequate to account for either load change scenarios.
 (34)
(34)
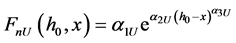 (35)
(35)
Here FnL denotes the normal contact load due to both elastic and plastic interaction of surface roughness, and FnU is the normal contact force due to only elastic interaction of the roughness. When the disturbance is small, the above force equations can be written in
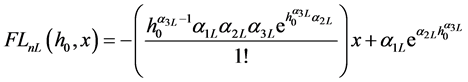 (36)
(36)
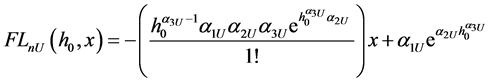 (37)
(37)
linear form using truncated Taylor series expansion of FnL and FnU about the equilibrium minimum separation. Figure 4 illustrated the contact forces along with their linear estimates about an equilibrium position for a relatively high plasticity index. The area between the load and unload forces represents energy loss per cycle. Figure 5 shows a similar force history corresponding to a lower value of the plasticity index. As expected the area between the load and unload phases are reduced to zero for a plasticity index of 0.5, since it corresponds to elastic behavior of contact. It is a simple task to estimate the energy loss per cycle. We can perform integration of force over displacement in the load and unload phases and obtain the energy loss in a single cycle. For amplitude of oscillation of xa from equilibrium, we can express the energy loss per cycle as follows.
![]()
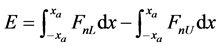 (38)
(38)
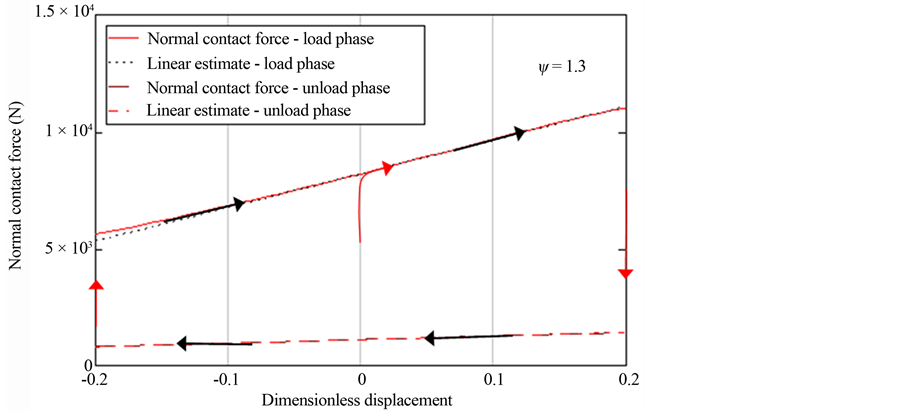
Figure 4. The schematic of load-unload phases in high plastic zone.

Figure 5. The schematic of load-unload phases in low plastic zone.
That can be simplified by using the linear approximation of each load function in Equations (36) and (37). We find
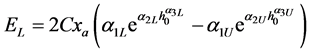 (39)
(39)
EL is the energy loss per cycle. The energy per cycle can be expressed in dimensionless form by dividing Equation (40) by Cxa. So the dimensionless energy loss per cycle is
 (40)
(40)
Figure 6 illustrates dimensionless energy per cycle and plasticity index as functions of dimensionless critical interference. When critical interference is low (high plasticity index), the interference enters the plastic regime for less contact load. Therefore, energy loss per cycle is higher for low critical interference. As critical interference increase, the number of asperities experiencing plastic interference decrease, thereby, reducing the energy per cycle. This is clearly shown to be the case in Figure 6. A similar plot, which directly relates energy loss per cycle to surface roughness, is shown in Figure 7. In this case the abscissa represents the dimensionless average radius of curvature. It is observed that as dimensionless asperity summit radius of curvature is increased (surface is made more smooth) the energy loss per cycle decreases.
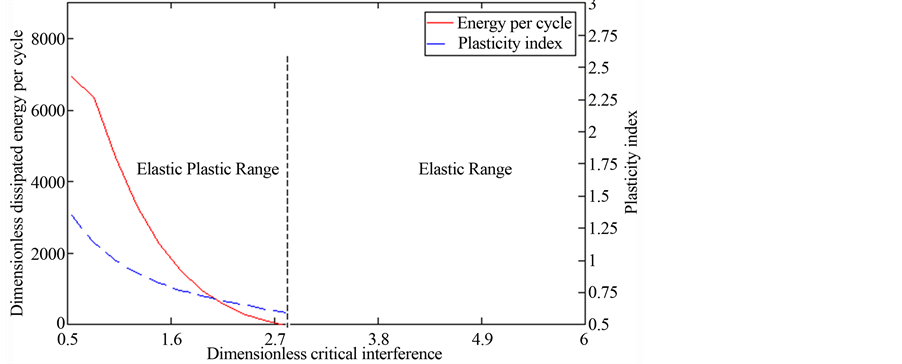
Figure 6. Dimensionless energy loss per and surface plasticity index versus critical asperity interference.

Figure 7. Dimensionless energy loss per cycle and surface plasticity index versus dimensionless average asperity summit radius of curvature.
Legal litigation regarding the use of similar implant material shed light on the difficulty faced in using similar material in hip implant replacement. Cobalt-Cobalt implant was alleged to result in excessive degradation of implant material, generating unacceptable amount of wear debris to the level of presenting toxicity in the patient. Based on the present study, use of Cobalt-Cobalt implant would require a very high level of surface finish to reduce plastic deformation. Consider, for example, the equation for plasticity index given by Greenwood and Williamson [39]
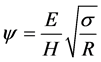
For Cobalt-on-Cobalt implant we can use the properties in Table 1 to find E = 62 GPa and H = 700 MPa. For average dimensionless asperity summit radius of curvature β =R/σ = 4600, we obtain a surface plasticity index of ψ = 1.3 which puts deformation in the plastic range. In fact to ensure that contact is in the elastic range, the surface finish must be enhanced to a degree that would result in β = 21,600, an unrealistically high number. This result is consistent with the latest news regarding the failure of many implants involving metal-on-metal material. Figure 7 corresponds to typical ranges when dissimilar materials are used in hip implant. For Cobalt-Polyethylene, we use E = 0.75 GPa, and H = 120 MPa (Table 1) for the Polyethylene, the softer material, and β = 25, the surface plasticity index ψ = 0.953, putting the contact in the elastic-plastic range, whereas for β = 112, the plasticity index reduces to ψ = 0.586, yielding elastic contact. The plot in Figure 8 well represents this range. The advantage of using dissimilar material is clearly shown in the above discussion. It is easy to obtain surface finish that would yield an elastic interaction at the contact of femoral head and acetabulum implant if one employs dissimilar material, while using similar material, such as Cobalt-Cobalt, is quite problematic since to guarantee elastic contact the surface finish requirement are not attainable.
3. Contact Frequency and Damping
It is possible to define contact frequency and damping if one is able to define an appropriate equivalent lumped mass near the interface of femoral head and acetabulum. Designating the lumped mass as m0, Equations (36) and (37) can be used in a nonlinear dynamic model of the contact to obtain contact frequency and damping ratio as follows:
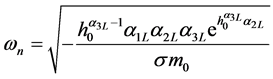 (41)
(41)
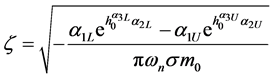 (42)
(42)
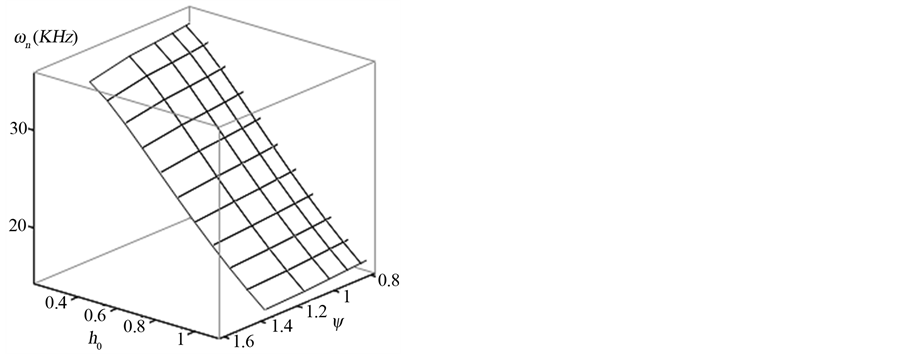
For an assumed m0 = 0.1 kg, Figure 8 depicts the resulting natural frequency and damping ratio versus the
Table 1. Material and surface properties used.
 (a)
(a)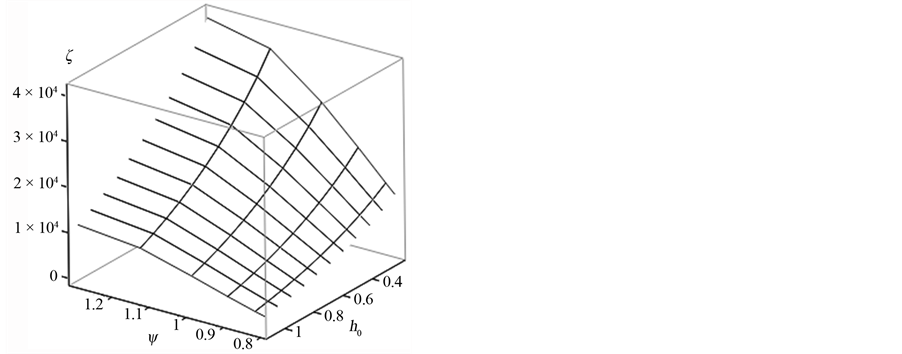 (b)
(b)
Figure 8. Contact natural frequency and damping ratio vs. minimum surface separation.
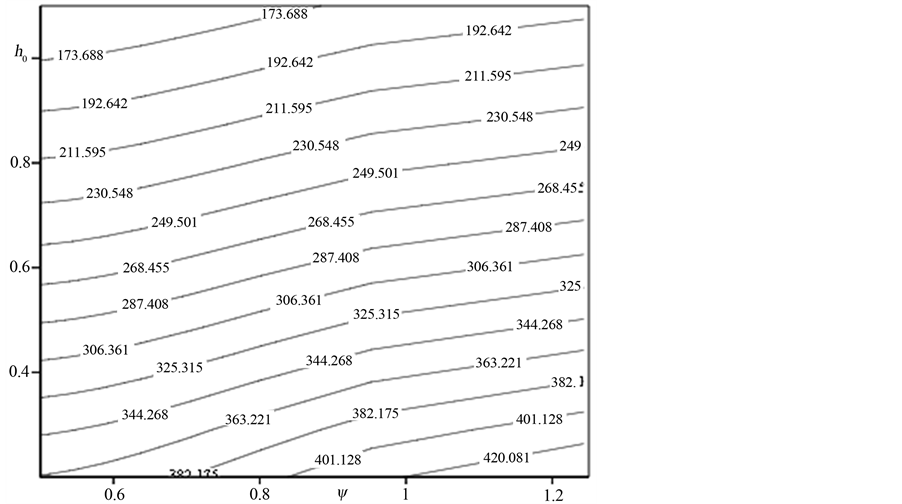
minimum dimensionless mean surface separation. Figure 9 shows the contour plots of the same. One should note that the dimensionless minimum separation corresponds to a certain contact load. Lower values of h0 correspond to higher contact force and vice versa. It is interesting to note that natural frequency primarily changes with contact load (or h0) and not the surface plasticity index. This is consistent with the fact that contact presents a nonlinear overall stiffness and therefore stiffness is increased with increase in contact load. Higher stiffness in turn means larger contact frequency. Figures 8 and 9(b) show contact damping ratio. It is clear that damping ratio depends on both applied contact force and surface plasticity index. It is noted here that the sensitivity of contact damping ratio to plasticity index increases for higher contact force (lower h0).
4. Closing Remarks
This paper has developed an elastic-plastic contact model of hip joint implant. The model treats femoral and acetabulum implants as spherical solids in internal conformal contact and accounts for the roughness effects of both surfaces. An equation relating force to minimum mean surface separation was derived using statistical integral over contact region of effective interaction. Approximate equation describing force explicitly in terms of minimum separation was obtained and used to find closed-form equation for contact energy loss per cycle. It is shown that energy loss per cycle varies with plasticity index of the surface of the weaker implant. For an assumed lump mass representation at contact of implant, the utility of the approximate equations was exemplified by deriving expressions for contact natural frequency and damping ratio.
The specific contributions of this paper include:
- Inclusion of implant surface roughness in hip implant contact model
- Explicit function for hip implant for a considerable range of hip implant joint sizes
- Energy loss per cycle related to macro and micro geometry of the implant surfaces o Closed-form equations for hysteretic energy loss per cycle were obtained using load/unload process at the hip implant surfaces. The energy per cycle was related explicitly to the material properties and surface statistics of the implant.
- Characterization of hip implant natural contact frequency and contact damping Simulation of load/unload process on hip implant using similar material, Cobalt-Cobalt, and dissimilar material, Cobalt-Polyethylene, for the femoral head and acetabulum showed that:
- Similar implant material was more prone to plastic deformation, thereby suggesting the increased possibility of wear. Cobalt-Cobalt contact required an unreasonably high surface finish to minimize plastic energy loss. Such high requirement of surface finish is impractical and even if possible would be highly costly.
- Dissimilar implant material was shown to be superior in that it is easier to guarantee elastic contact so that the plastic energy loss is minimized for a practical range of surface roughness.
The above result is consistent with recent issues related to the use of similar material in hip implant. Recent litigation won by an implant patient in California against Johnson and Johnson related to failed implant due to
 (a)
(a) (b)
(b)
Figure 9. Contour plot of natural frequency and damping ratio vs. minimum surface separation and plasticity index. (a) Contact frequency; (b) Contact damping ratio.
the generation of excessive wear and the resulting toxicity. According to the news, the reason was primarily due to the use of metal-on-metal in the hip implant. Many more lawsuits relating to the metal-on-metal contact in hip implants against Johnson and Johnson are being submitted to the courts.
The potential usefulness of the results on estimation of hip implant contact stiffness and damping can involve the issue of potential vibration and noise generation. These not only can result in accelerated fatigue wear of implant surfaces but also can relate to implant recipient’s comfort level.
References
- Hodge, W.A., Fijan, R.S., Carlson, K.L., Burgess, R.G., Harris, W.H. and Mann, R.W. (1986) Contact Pressures in the Human Hip Joint Measured in Vivo. Proceedings of the National Academy of Sciences, 83, 2879-2883. http://dx.doi.org/10.1073/pnas.83.9.2879
- Bergmann, G., Deuretzbacher, G., Heller, M., Graichen, F., Rohlmann, A., Strauss, J. and Duda, G.N. (2001) Hip Contact Forces and Gait Patterns from Routine Activities. Journal of Biomechanics, 34, 859-871. http://dx.doi.org/10.1016/S0021-9290(01)00040-9
- Bergmann, G. (1998) Data Collection of Hip Joint Loading on CD-Rom. Free University and Humboldt University, Berlin.
- Pramanik, S., Agarwal, A.K. and Rai, K.N. (2005) Chronology of Total Hip Joint Replacement and Materials Development. Trends in Biomaterials & Artificial Organs, 19, 15-26.
- Charbonnier, C., Schmid, J., Kolo-Christophe, F., Magnenat-Thalmann, N., Becker, C., and Hoffmeyer, P. 2009, “Virtual Hip Joint: from Computer Graphics to Computer-Assisted Diagnosis”, Eurographics,.
- Montecucchi, P.C. (2002) Total Anatomic Hip Prosthesis. Montegen, 540 Beverly Court, Suite1-Tallahassee FL 32301 USA, Via G. Dezza n. 24 - 20144 Milan, Italy.
- Mc Laurin, C.A. (1954) Hip Disarticulation Prosthesis. Report 15, Prosthetic Services Centre, Department of Veterans Affairs, Toronto.
- Richards, S. and Richards, N. (1994) Artificial Hip Joints. Applying Weapons Expertise to Medical Technology, E&TR.
- Klein, M. (2005) Using Data in Making Orthopedic Imaging Diagnoses. Advances in Experimental Medicine and Biology, 44, 104-111. http://dx.doi.org/10.1007/0-387-32025-3_10
- Yusoff, S.F. (2009) Knee Joint Replacement Automation Templates. M.sc Thesis, Universiti Kebangsaan Malaysia, Bangi.
- Arora, J., Sharma, S. and Blyth, M. (2005) The Role of Pre-Operative Templating in Primary Total Knee Replacement. Knee Surgery, Sports Traumatology, Arthroscopy, 13, 187-189. http://dx.doi.org/10.1007/s00167-004-0533-5
- Kosashvili, Y., Shasha, N., Olschewski, E., Safir, O., White, L., Gross A. and Backstein, D. (2005) Digital Versus Conventional Templating Techniques in Preoperative Planning for Total Hip Arthroplasty. Canadian Journal of Surgery, 52, 6-11.
- Shapi, A., Sulaiman, R., Hasan, M.K. and Kassim, A.Y.M. (2011) An Automated Size Recognition Teqnique for Acetabular Implant in Total Hip Replacement. International Journal of Computer Science & Information Technology (IJCSIT), 3, 2.
- Hiroyuki, M., Takayoshi, H., Yoshitake, U., Shuji, U., Nobuyoshi, T. and Osamu, N. (2010) Evaluation of RF Heating on Hip Joint Implant in Phantom during MRI Examinations. Japanese Journal of Radiological Technology, 66, 25- 733.
- Zhang, W., Titze, M., Cappi, B. and Writz, D.C. (2010) Improved Mechanical Long-Permrealiability of Hip Resurfacing Prostheses by Using Silicon Nitride. Journal of Materials Science: Materials in Medicine, 21, 3049-3057. http://dx.doi.org/10.1007/s10856-010-4144-z
- Scifert, C.F., Brown, T.D. and Lipman, J.D. (1999) Finite Element Analysis of a Novel Design Approach to Resisting Total Hip Dislocation. Clinical Biomechanics, 14, 697-703. http://dx.doi.org/10.1016/S0268-0033(99)00054-6
- Phillps, A.T.M., Pankaj, P., Howie, C.R., Usmani, A.S. and Simpson, A.H.R.W. (2006) 3D Non-Linear Analysis of the Acetabular Construct Following Impaction Grafting. Computer Methods in Biomechanics and Biomedical Engineering, 9, 125-133. http://dx.doi.org/10.1080/10255840600732226
- Jonathon, R., Campbell, P. and Mathew, P.E. (2013) Metal Release from Hip Prostheses: Cobaltand Chromium Toxicity and the Role of the Clinical Laboratory. Clinical Chemistry & Laboratory Medicine, 51, 213-220.
- Steens, W., Foerster, G.V. and Katzer, A. (2006) Severe Cobalt Poisoning with Loss of Sight after Ceramicmetal Pairing in a Hip”—A Case Report. Acta Orthopaedica, 77, 830-832. http://dx.doi.org/10.1080/17453670610013079
- Tower, S.S. (2012) Arthroprosthetic Cobaltism Associated with Metal on Metal Hip Implants. BMJ, 344-430.
- Alan, M.K. and Swarts, E. (2009) Corrosion of a Hip Stem with a Modular Neck Taper Junction: A Retrieval Study of 16 Cases. The Journal of Arthroplasty, 24, 19-23.
- Brodner, W., Bitzan, P., Meisinger, V. and Kaider, A. (1997) Elevated Serum Cobalt with Metal-on-Metal Articulating Surfaces. The Journal of Bone and Surgery, 79-B, 316-321. http://dx.doi.org/10.1302/0301-620X.79B2.7326
- Senapati, S.K. and Pal, S. (2002) Uhmwpe-Alumina Ceramic Composite, an Improved Prosthesis Materials for an Artificial Cementted Hip Joint. Trends in Biomaterials & Artificial Organs, 16, 5-7.
- Colombi, P. (2002) Fatigue Analysis of Cemented Hip Prosthesis: Damage Accumulation Scenario and Sensitivity Analysis. International Journal of Fatigue, 24,739-746. http://dx.doi.org/10.1016/S0142-1123(01)00204-3
- Lennon, A.B. and Prendergast, P.J. (2002) Residual Stress Due to Curing Can Initiate Damage in Porous Bone Cement: Experimental and Theoretical Evidence. Journal of Biomechanics, 35, 311-321. http://dx.doi.org/10.1016/S0021-9290(01)00216-0
- Zimmerman, S., Hawkes, W.G., Hudson, J.I., Magaziner, J., Hebel, J.R., Towheed, T., Gardner, J., Provenzano, G. and Kenzora, J.E. (2002) Outcomes of Surgical Management of Total Hip Replacement in Patients Aged 65 Years and Older: Cemented versus Cementless Femoral Components and Lateral or Anterolateral versus Posterior Anatomical Approach. Journal of Orthopaedic Research, 20, 182-191. http://dx.doi.org/10.1016/S0736-0266(01)00090-0
- Stolk, J., Maher, S.A., Verdonschot, N., Prendergast, P.J. and Huiskes, R. (2003) Can Finite Element Models Detect Clinically Inferior Cemented Hip Implants? Clinical Orthopaedics and Related Research, 409, 138-150. http://dx.doi.org/10.1097/01.blo.0000058882.03274.5e
- Waide, V., Cristofolini, L. and Toni, A. (2004) An Experimental Analogue to Model the Fibrous Tissue Layer in Cemented Hip Replacements. Journal of Biomechanical Materials Research (Part B Applied Biomaterials), 64B, 232-240. http://dx.doi.org/10.1002/jbm.b.30004
- Li, C., Granger, C., Schutte Jr., H.D., Biggers Jr., S.B., Kennedy, J.M. and Latour Jr., A.R. (2003) Failure Analysis of Composite Femoral Components for Hip Arthroplasty. Journal of Rehabilitation Research and Development, 40, 131-146. http://dx.doi.org/10.1682/JRRD.2003.03.0133
- Kowalczyk, P. (2001) Design Optimization of Cementless Femoral Hip Prostheses Using Finite Element Analysis. Journal of Biomechanical Engineering, 123, 396-402.
- Stolk, J., Verdonschot, N., Cristofolini, L., Toni, A. and Huiskes, R. (2002) Finite Element and Experimental Models of Cemented Hip Joint Reconstructions Can Produce Similar Bone and Cement Strains in Pre-Clinical Tests. Journal of Biomechanics, 35, 499-510. http://dx.doi.org/10.1016/S0021-9290(01)00213-5
- Ni, G.X., Lu, W.W., Chiu, K.Y. and Fong, D.Y. (2005) Cemented or Uncemented Femoral Component in Primary Total Hip Replacement? A Review from a Clinical and Radiological Perspective. Journal of Orthopaedic Surgery, 13, 96-105.
- Prendergast, P.J. (1997) Review Paper—Finite Element Models in Tissue Mechanics and Orthopaedic Implant Design. Clinical Biomechanics, 12, 343-366. http://dx.doi.org/10.1016/S0268-0033(97)00018-1
- Phillipsab, A.T.M., Pankajb, P., Howiec, C.R., Usmanib, A.S. and Simpsonac, A.H.R.W. (2006) 3D Non-Linear Analysis of the Acetabular Construct Following Impaction Grafting. Computer Methods in Biomechanics and Biomedical Engineering, 3, 125-133. http://dx.doi.org/10.1080/10255840600732226
- Stansfield, B.W. (2003) Direct Comparison of Calculated Hip Joint Contact Forces with Those Measured Using Instrumented Implants. An Evaluation of a Three-Dimensional Mathematical Model of the Lower Limb. Journal of Biomechanics, 36, 929-936. http://dx.doi.org/10.1016/S0021-9290(03)00072-1
- Kaddick, C., Stur, S. and Hipp, E. (1997) Mechanical Simulation of Composite Hip Stems. Medical Engineering & Physics, 19, 431-439.
- Hurwitz, D.E., Foucher, K.C. and Andriacchi, T.P. (2003) A New Parametric Approach for Modeling Hip Forces During Gait. Journal of Biomechanics, 36, 113-119.
- Sepehri, A. and Farhang, K. (2007) An Extension of CEB Elastic-Plastic Contact Model. Proceedings of the STLE/ ASME International Joint Tribology Conference, San Diego, 22-24 October 2007, 597-599.
- Greenwood, J.A. and Williamsom, J.B.P. (1966) Contact of Nominally Flat Surfaces. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 295, 300-319.
- Chang, W.R., Etsion, I. and Bogy, D.B. (1987) An Elastic-Plastic Model for the Contact of Rough Surfaces. Journal of Tribology, 109, 257-263. http://dx.doi.org/10.1115/1.3261348
Nomenclature
C a surface constant
E equivalent modulus of elasticity of the two surfaces
E1 modulus of elasticity of the femoral implant
E2 modulus of elasticity of the acetabulum implant
EL energy loss per cycle
F total contact force
FnL normal contact load due to elastic-plastic interaction of roughness
FnU normal contact load due to elastic interaction of roughness
h mean plan separation
h0 minimum separationm0 mass of femoral head
Pe(h) elastic force per unit nominal area
Pp(h) plastic force per unit nominal area
P(h) contact force per unit nominal area
R1 radius of femoral head
R2 radius of acetabulum
s ratio of an asperity height over the standard deviation
ωc critical interference
x a disturbance from equilibrium
xa amplitude of oscillation
α1L, α2L, and α3L coefficients in the approximate function for loading phase
α1U, α2U, and α3U coefficients in the approximate function for unloading phase
β dimensionless equivalent average asperity radius of curvature
β1 average asperity radius of curvature of the femoral implant
β2 average asperity radius of curvature of the acetabulum implant
δ offset between sphere centers
ζ damping ration
η the asperity density per unit area
θ angular location
υ1 Poisson ratio of the femoral implant
υ2 Poisson ratio of the acetabulum implant
σ standard deviation of asperity height
ψ plasticity index
ωn natural frequency


