Journal of Biomedical Science and Engineering
Vol.6 No.9(2013), Article ID:37152,11 pages DOI:10.4236/jbise.2013.69112
Aortic endovascular repair modeling using the finite element method
![]()
Université de Lyon, CNRS INSA-Lyon, LaMCoS, UMR5259, F-69621, Lyon, France
Email: ghizlane.mouktadiri@hotmail.fr, benyebka.bou-said@insa-lyon.fr
Copyright © 2013 Ghizlane Mouktadiri et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 16 July 2013; revised 25 August 2013; accepted 12 September 2013
Keywords: AAA; Endovascular Repair; FEA; Composite; Nonlinearity
ABSTRACT
Aim: The goal is to simulate different stages of the endovascular procedure in the preoperative phase. Methods: We have developed a numerical model of the endovascular treatment of abdominal aortic aneurysms (AAA) using finite element analysis (FEA), we took into account the geometry of the biological region reconstructed from scans, a local characterization of the guidewire/catheter mechanical properties, a mapping of material properties depending on the degree of calcification, a real behavior of the vascular walls, and a projection of the aorta environment. Results: Our results present the endovascular system navigation from the femoral artery to the neck of the aneurysm, predict the deformation of femoral, iliac and aortic arteries while driving flexible and stiff endovascular devices, and detect stress concentration due to tortuous and calcified artery zones. A given group of patients with very angulated and calcified arteries were validated, based on a tuning between clinical data and our endovascular simulation. Conclusion: Our model allows controlling with accuracy the delivery system rise during surgery, predicting the feasibility of the surgery with reliability as well as choose the best guide for each patient, taking into account the risk of rupture of calcified areas in the case of high angulations, and using planning simulated images with deformation of artery walls to propose stent sizing.
1. INTRODUCTION
The Abdominal Aorta Aneurysm (AAA) is a cardiovascular disease that affects 6% - 7% of the Western population and its incidence increases with age [1-3]. At least 90% of AAA is affected by atherosclerosis because of high cholesterol, inflammation, infection or tobacco [4]. Most of these aneurysms are located near bifurcation [5]. The rupture of the aneurysm is a dangerous and potentially fatal accident whose incidence is increased by arterial hypertension [2].
For over 50 years, open surgery was the only treatment of AAA. This is a major procedure with considerable risk of cardiac complications (myocardial infarction), respiratory problems, bleeding, renal difficulties, as well as infection and colic (risk of ischemic colitis) [2]. However, since 1991, a new mini-invasive surgical procedure has been introduced. The endovascular procedure involves dragging a stent through a release device of the femoral artery to the level of the aneurysm.
This technique has several advantages such as shorter hospital stay, smaller incisions, and faster recovery. However, current clinical results in the long term are not significantly different when compared to conventional surgery [6], and have failed to show that these procedures can be performed with lower morbidity and mortality [7].
However, due to complications arising from their implementation, the reliability of these new methods of treatment remains a subject for discussion [8]. The main complications that can occur are:
• During the surgery: difficulties of navigation of the guidewire and catheter, resulting from strong tortuous form of the arteries and significant calcification of the arterial walls…, may cause stress concentration and, consequently, a risk of rupture [9-11].
• After the surgery: the phenomena of migration and endoleaks [12-16] related to poor design of the stent are not yet fully mastered [17]. Not taking into account the deformation of the artery under the action of the release device may be the cause of poor sizing, positioning and choice of the stent [18-20].
Numerous research scientists have attempted to understand the biomechanics of the diagnosis or clinical treatment [21-23] and to make improvements to this intervention. Let us recall that it is minimally invasive and can treat complex arterial pathologies (aneurysms, stenosis, embolisms, etc.), using an endovascular guidewire, the catheter containing the stent and a sheath. Despite major progress in this technology (new devices and techniques), anatomical factors of specific patients make handling of the catheter very difficult and require considerable technical skill. The more we are confronted with complex cases, the more ambitious the endovascular procedure becomes, and mastering of endovascular skills becomes difficult [24].
For this purpose, we have developed a numerical simulation tool to assist the surgery. It contributes to the improvement of therapeutic endovascular procedures in terms of accuracy and optimizes the intervention strategy.
This tool takes into account: 1) the actual biological geometry reconstructed from preoperative clinical images on a specific group of patients with a tortuous artery surface and calcification, 2) local characterization of mechanical properties of the endovascular system, 3) mapping of mechanical properties of soft tissue based on its degree of calcification (safe, calcified, thrombus), 4) projection of the real environment of the artery on the simulated model for each patient, 5) pre-stress, and 6) the material and geometric non-linearity of the composite model for the wall artery.
The main objectives of this complete modeling of the endovascular procedure are:
• Simulation of all treatment steps using patient specific data.
• Specifying control of the endovascular system navigation and stent deployment during the surgery procedure.
• Detecting the risks of perforation due to tortuous and calcified areas while transporting the more rigid endovascular devices.
• Providing augmented reality tools to surgeons for the 3D geometry of deformed artery with calcified and tortuous walls for pre-operative treatment during surgery.
• Determining deformation of the anatomical structure under the action of the deployment device (stiff guidewire and catheter with stent).
• Verifying the presence of endoleaks and migration using planning images with and without deformation after stent deployment.
• Study of the biological tissue flexibility by the navigation of various surgical tools (flexible and rigid), for better choices of guidewire and catheter.
2. MATERIALS AND METHODS
2.1. Nano-Biomechanical Characterization of the Anatomical Structure
Numerical modeling of endovascular treatment of AAA requires knowing the biomechanical properties of arterial vessels throughout the path traveled by guidewire catheter device from the femoral to the abdominal aorta. Due to the lack of data on the mechanical properties due to the degree of calcification [25], we propose to perform mechanical testing of human arterial tissue that allows distinguishing calcified walls, pathological or healthy, and to integrate these mechanical characteristics according to the degree of calcification in numerical model.
Femoral, iliac and aortic samples of aged patients were tested after being stored and dissected Figure 1. The dissection is performed as a function of parietal quality: data scanners that contain indications as “grid level” on
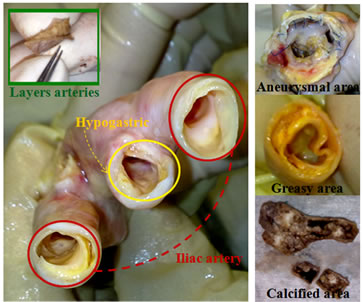
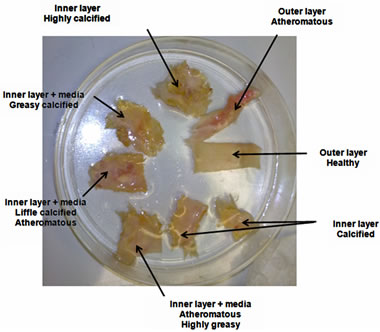
Figure 1. Clinical arterial samples of aged patients, cut according to the degree of calcification and immersed in conservation solution.
the state of arterial tissue were translated in terms of mechanical properties.
For this purpose, an atomic force microscope (AFM), a tribometer and rheometer were used to characterize the mechanical behavior in compression, shearing and friction of different layers of arteries Figure 2 as function of the degree of calcification. A large number of samples (474) were tested in a liquid environment (Phosphate buffered saline PBS pH 7.4) at room temperature.
Figure 3(a) depicts the number of events as a function of adhesion force to verify the low bond strength hypothesis in the theory of contact. Thereafter, for each sample, we measured the indentation force as a function of depth for different speeds. Compression and decompression paths do not always overlap. This explains the effect of some visco-plastic arterial walls properties Figure 3(b). Only the elastic part is retained for the measurement of mechanical properties, using AFM tools, we measured the normal load as function of the indentation. However, different theories of elastic contact have been proposed to improve the description of contact between two solid bodies: Hertz [26,27] [1889], Sneddon [1965], Johnson, Kendall and Roberts (JKR) in [1971], Derjaguin, Muller and Toporov (DMT) in [1975]. The Hertz model, in a liquid medium with the assumption of weak Vander-Waals intermolecular adhesion forces (capillarity), was adapted to characterize the tip-sample contact:
Thus, the relationship Equation (1) between force Fn and indentation δ for a sphere of radius R is:
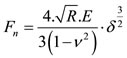 (1)
(1)
For a cone of half-tip angle ϕ, we find Equation (2):
 (2)
(2)
E: Elastic modulus and ν: Poisson coefficient.
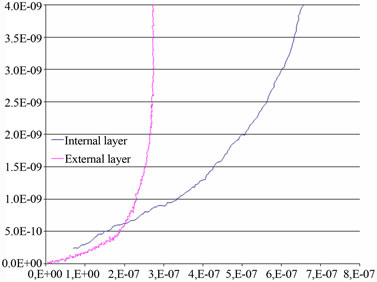
An example is shown below of test results on an internal and external layer of a fatty artery. We find that the outer layer is more rigid than the inner layer Figure 4(a), and that the viscoelastic effect at the nanoscale is negligible, because the modulus of elasticity is not strongly

Figure 2. Experimental device. Mechanical tests of the arterial samples on the AFM in the presence of the conservation fluid.
 (a)
(a)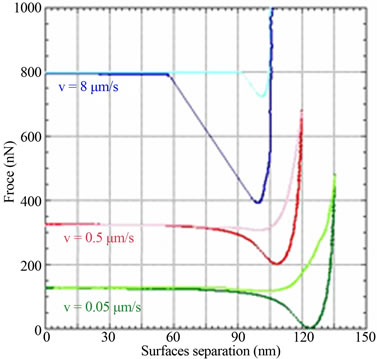 (b)
(b)
Figure 3. a) Samples treated as function of adhesion forces; b) Treatment of characteristic force-distance curves.
affected by the indentation velocity Figure 4(b).
One of the test results concerns measuring tangential forces and deducing the friction coefficient depending on the degree of calcification for the internal layer of a highly calcified artery. This coefficient is the ratio between the normal force that is imposed by gravity and the tangential force that is measured. The variation of this coefficient is recorded with time. Figure 5 represents the surface topography of the involved sample. Thus, the friction curve shows positive and negative parts, each corresponding to an alternating displacement. The friction coefficient remains stable over time. It is
 (a)
(a) (b)
(b)
Figure 4. a) The force (nN) as function of displacement (nm) for the inner and the outer layer of a very fatty artery; b) Normal force according to the indentation at different speeds.
about 0.5 for very calcified areas.
The assessment of tests on different human arterial samples has led to a determination of nano-mechanical properties of different layers as a function of the degree of calcification. This was done through preoperative images of the wall artery as shown in Figure 6. We connected each grid point to a mechanical property such as elastic modulus and friction coefficient.
• 2.2. Local Mechanical Characterization of the Guidewire and Catheter
• The guidewire In this section, our goal is to make a local characterization of the mechanical properties of the guidewire catheter device, as input to a numerical endovascular model predicting the deformation of the anatomical
 (a)
(a)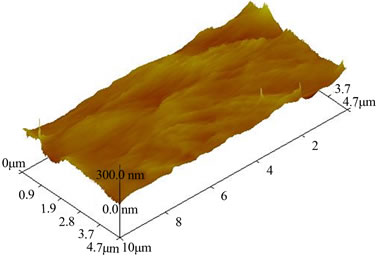 (b)
(b)
Figure 5. a) Coefficient of friction as function of time (s); b) Roughness of the arterial surface.
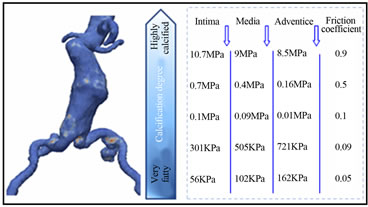
Figure 6. Mapping elastic modulus and friction coefficient depending on the degree of calcification.
structure under the action of this device.
• The folding stent: Catheter This system contains the stent; it has a 0.889 mm internal diameter, that allows its navigation in interaction with the guide. It is also composed of several areas: the tip with variable diameter, the area containing the stent, the tubular area, and the sheath. It is of variable construction (platinum-iridium, nickel, nitinol, polyester, etc.).
To create a model and to understand the mechanical behavior of the guidewire and catheter devices, tests were conducted for each region, considering the variation of mechanical properties according to various medical tools. The 3D image correlation was found to be the best tool to follow this variation.
The tests were performed on the tensile machine. A speckled black on white is applied to the tested sample. This is then subjected to uniaxial quasi-static tension and is fixed between the two jaws of the LFPlus machine, which is connected to an image acquisition system, lighting and 3D correlation Figure 7.
The results were obtained through a local characterization (3D correlation and extensometer) and global one. The curves in Figure 8 show one example of mechanical tests results on the catheter tip. We measured stress versus strain to obtain value of Young’s modulus. Figure 9 is an example of a summary of mechanical properties (elastic modulus and Poisson’s ratio) as a function of

Figure 7. Experimental device: Mechanical testing of endovascular tools (guidewire and catheter) using LFPlus machine.
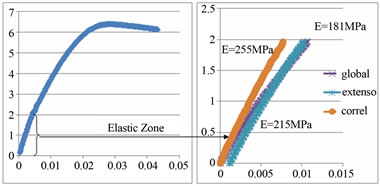
Figure 8. Stress (MPa) as function of strain.
 (a)
(a)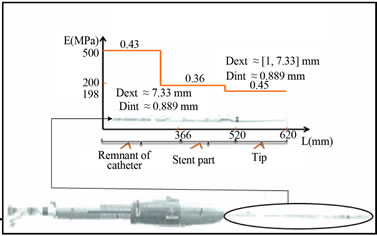 (b)
(b)
Figure 9. Summary of mechanical properties: a) Guidewire (Radiofocus); b) Catheter (Medtronic).
position on the endovascular system (guidewire and catheter).
We note a very significant stiffness gradient between the tip and the stiff zone of the guide, which is added gradually in the transition area. The tips of different guides used in the clinical setting have a stiffness between 700 to 2000 MPa. The purpose is to make easier the navigation of the guidewire in vessels without pain and improve the contact between the guide head and blood vessels, while the rigid part is in the range of 11,800 to 19,000 MPa to make the artery straight.
2.3. Finite Element Analysis Model
After creating a functional relation for the mechanical properties of biological tissues and surgical tools, a simulation is possible to predict all steps of endovascular treatment using patient specific data and the behavior of arterial walls under the action of the guidewire and the catheter system.
Creating a model of the complete system guidewire/ catheter/aortic/femoral/iliac/aneurysm/environment of the artery requires the separate modeling of its different components. The originality of this study is as follows:
Consideration of a realistic geometry of the biological system reconstructed from preoperative clinical images on a specific group of patients with high tortuosity and calcification.
Accounting for the environment of the artery, the degree of calcification, the reference geometry with preload, and the nonlinear behavior of materials and geometry.
Considering frictional contact behavior between arterial walls and the surgical tools, and between the tools themselves.
A composite model for biological tissue including fiber orientation.
The computer code used is Abaqus 6.10-1. We used Updated Lagrangian description due to large deformations. The arterial walls were modeled using thin shell theory with Kirchhoff approach. The delivery system was modeled using Timoshenko beam elements.
Considering the strong nonlinearity of the problem, the explicit time integration scheme is a relatively easy numerical scheme to implement and less expensive in terms of computation time [28,29]. Thus we adopted the method β-2, which allows the introduction of a numerical damping coefficient that removes the high frequencies [30]. The contact between the tools and biological tissues was managed by unilateral penalty conditions, which consist of increasing the functional of total energy by a penalty function [31]. This contact represents the interaction between tools and soft tissues by a spring with a stiffness depending on the penetration. Femoral, iliac, and aortic wall thickness models have been introduced, varying from 1 to 2 mm.
The models were created using preoperative individual patient data. A three-dimensional scan of the patient is performed with a contrast injection to reveal the arrangement of blood vessels located around the area of interest Figure 10.
Initially, a manual step is necessary. It consists of extracting the vessel centerline, the lumen of the artery by splines, and the planes orthogonal to the neutral line depending on the degree of curvature of the artery wall.
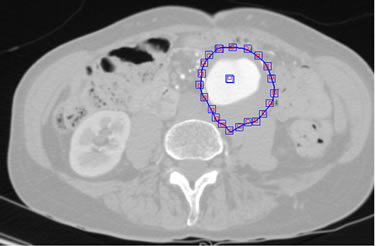
Figure 10. Creating splines and the centerline from a scan on a aged patient.
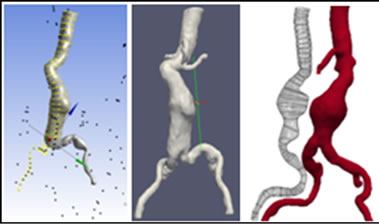
Then a reconstruction of the aneurysm is done, including bifurcations. The iliac and tortuous femoral artery is the final geometry to be used for simulation Figure 11.
This technique has the advantage of generating a geometry which is very close to the real one.
In order to overcome convergence difficulties due to the complex geometry, and problems arising from the contact between the endovascular tools and the arterial walls; only the aorta, femoral and internal iliac used for endovascular instruments navigation are included in the analysis. The external iliac and secondary vessels are taken into account using appropriate boundary conditions.
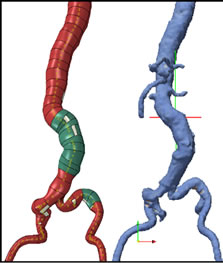
- The artery was modeled using composite materials. It is considered as a matrix material with three layers that are reinforced by two families of fibers. Therefore its mechanical properties depend on both directions of the fibers. The orientation of collagen fibers was observed by microscopy in the layers of the human aorta, on the order of 10˚ on average for the collagen fibers in the
 (a)
(a)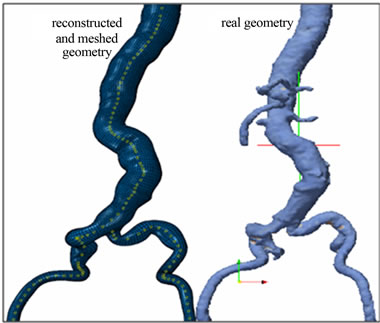 (b)
(b)
Figure 11. a) Geometric reconstruction from preoperative images; b) Real geometry; c) Projection of the reconstructed geometry on the real geometry, d) Mesh geometry.
media, and 40˚ in the adventitia have been found [32]. These results are in accordance with the histologic findings of a general human abdominal aortic media.
- Environmental information of the artery was taken into from the data of the scanner images. We extracted the list of the nearest points of the spline, the centerline and secondary branches of the artery. Thus, we have represented this environment by elastic supports Figure 12(a).
- Information on the condition of the arterial wall was described in the numerical model. Information related to the distribution of the degree of calcification, which can differentiate healthy areas from aneurysmal and calcified regions was projected in the numerical model Figure 12(b).
Environmental information of the artery was taken into
- Information on the condition of the arterial wall was described in the numerical model. Information related to the distribution of the degree of calcification, which can differentiate healthy areas from aneurysmal and calcified regions was projected in the numerical model Figure 12
Healthy and aneurysmal areas were modeled as a hyper-elastic material with Mooney-Rivlin constitutive Equation (3), while calcified areas have been considered as linear elastic Figure 13:
 (3)
(3)
where
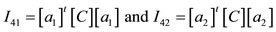 (4)
(4)
with W is the energy density of Mooney-Rivlin, I1, I2, I3 are the strain invariants, I41 and I42 describe the square
 (a)
(a) (b)
(b)
Figure 12. a) Projection artery environment of the scan in the corresponding numerical model; b) Projection parietal quality of data in the simulated model.
 (a)
(a)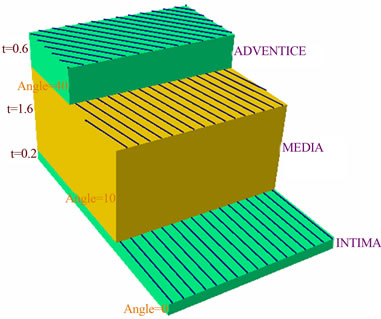 (b)
(b)
Figure 13. a) Representation of healthy and aneurysmal areas by hyper-elastic model, and calcified areas by linear elastic model; b) representation of layers and collagen fibers of the artery.
stretching fibers, characterized by the directions a1 and a2 (anisotropy terms), a01 and a10 are the constants parameters of Mooney-Rivlin, [C] Cauchy Green tensor, k1 and k3 are material parameters, k2 and k4 are dimensionless parameters, generated by two families of fibers and k is the bulk modulus.
The Mooney-Rivlin anisotropy terms present the energy stored in the fibers, they are described by exponential functions.
In their normal physiological condition, the arteries are in a state of longitudinal elongation and generally subject to internal pressure. This means that the stress straint is non-zero when the vascular smooth muscle is inactive. This hypothesis was justified by several experimental studies on normal and decellularized arteries and revealed the existence of significant residual stresses within the arterial wall [33,34]. In our model, we considered the reference state of the artery corresponding to the nonzero stress state when the intravascular pressure is zero. This pre-stress was estimated from a state of unknown geometry, subjected to a positive pressure that can reproduce the real reference geometry extracted from the preoperative data.
3. RESULTS AND DISCUSSIONS
The finite element simulation of endovascular aortic aneurysm treatment of a selected patients group with a very strong angulation and calcification has enabled 3D visualization of the guidewire and catheter navigation from the incision area to the neck of the aneurysm. Surgical tools are initially positioned at the entrance to the femoral, in the direction of the neutral line, and then a displacement is applied to the lower base of the guide and the catheter.
Here are the results of one insertion of the guidewire and the catheter within a guide, for a given position of the endovascular tools including wall deformation at all treatment steps Figure 14, movie1.
The main objective of this simulation is to control the navigation of the medical device, in order to have virtual 3D images in real time of the manipulation of the guide. The guide is interacting with the arterial walls. The catheter interacts with the entire system. Thus we obtain the stress state at each step of navigation. Therefore it is possible to locate the stress peaks, and predict the risk of rupture due to curvature and calcification of the iliac and femoral artery. Figure 15 shows the stress distribution throughout the endovascular procedure. It allows the evaluation of the critical areas at the time of the ascent of the device and analyzes the maximum stress value with reference to failure models already established in the literature.
The numerical model was also used to simulate various endovascular devices most commonly used in the clinical environment. However, this simulation provides
Figure 14. Sub-steps of the navigation of the guidewire and the catheter interacting with the guidewire.
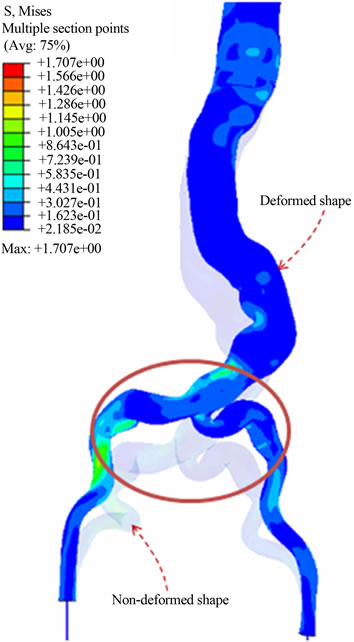
Figure 15. Stress distribution in blood vessels during the navigation of the endovascular system.
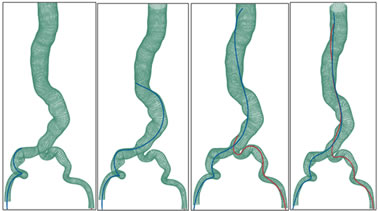
useful information for surgeons, to determine during the preoperative phase, the difficulties they may face. Thus, it allows refining the selection of a best guide for each patient. Figure 16 shows the flexibility of arterial walls under the action of different types of guide. It is observed that the behavior of blood vessels towards the flexible guide remains the same. The guide tends to warp and follow the path of the artery without distortion. As for the stiff guide, it stiffens and straightens the artery.
In order to get a biologically realistic simulation, the model has been validated by comparing the simulation results with preoperative clinical findings. Radiographs were performed to observe the final position of artery walls and deployment tools during injections of contrast. From these images, a projection of the simulation results in the same plane of the clinical images was used to compare the final geometry of the guide obtained by the simulation. The position of the guide in the preoperative phase obtained by surgeons is shown Figure 17(a). The
 (a)
(a) (b)
(b)
Figure 16. Flexibility of arterial walls under the action of different types of guidewires: a) flexible guide; b) stiff guide.
comparison between the results of the first simulation before tuning and clinical data show a significant difference.
However, the inaccuracy is due to not taking into account the environment of the artery. This is why other simulations were performed to gradually approach clinical reality. Elastic supports with the environment of the artery have been added in the numerical model Figure 17(b). Thus the final result is quite satisfactory Figure 17(c), and allows us to validate our numerical model of endovascular treatment of AAA.
The validation was done on a very specific group of patients, selected with a high degree of tortuosity and calcification. Thus, the clinical results match well with the simulated results.
4. CONCLUSIONS
The analysis of the results from endovascular treatment AAA using FEA for real patients-specific complicated geometry in terms of angulation and calcification demonstrates its potential impact:
• Precise control in real-time and with 3D visualization during the different stages of endovascular treatment of AAA.
• A feasibility study of endovascular surgery, and therefore an assessment of the state of stress in pre-
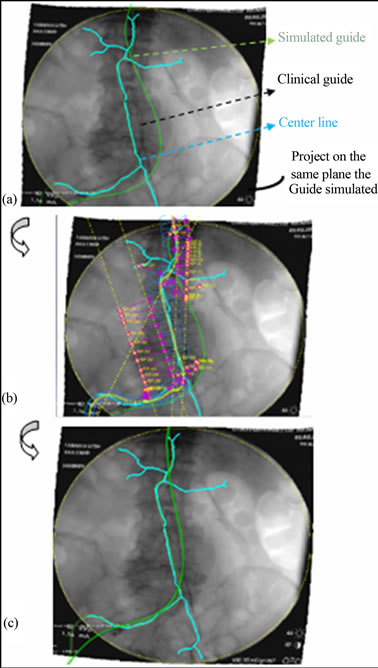
Figure 17. Projection of the simulated results on clinical outcomes. A) Before tuning between simulation results and preoperative data; (b)-(c) After tuning.
dicting the risk of damaging very tortuous and calcified arteries during simulation of the rise of endovascular tools.
• Assistance in the surgery, such as a better choice of surgical tools for each patient, and therefore a decrease in the number of endovascular tools used, and the radiation dose.
In addition, this model may be useful in the design of stents from the information given by the deformed state of the artery. At the current state of the technology, stent sizing using planning images without deformation does not take into account the morphological changes experienced by vessels during surgery, and therefore may bring an inaccuracy to the results. However, the present numerical model can contribute to understanding the causes of endoleaks and migration of stents and improving the outcome for many patients.
Future research should assess how this simulation can implement the present in vitro results to in vivo.
5. ACKNOWLEDGEMENTS
The authors would like to thank Dr Ana Maria Sfarghiu for her help to the experimental part. This work was supported by funds from the National Foundation of Research.
REFERENCES
- Rose, J.-L., Lalande, A., Bouchot, O., Bourennane, E.-B., Walker, P.M., Ugolini, P., Revol-Muller, C., Cartier, R. and Brunotte, F. (2010) Influence of age and sex on aortic distensibility assessed by MRI in healthy subjects. Magnetic Resonance Imaging, 28, 255-263. doi:10.1016/j.mri.2009.07.001
- Kasper, D.L., Braunwald, E., Fauci, A.S. and Hauser, S.L. (2006) Harrison: Principes de la médecine interne. 16th Edition.
- Mathieu Collette (2010) Les techniques de mesures: La rigidité artérielle. http://collettemathieu.blog.lemonde.fr/category/cours-sur-la-rigidite-arterielle/les-techniques-de-mesures/
- Wang, S., Zhang, C., Zhang, M., Liang, B., Zhu, H., Lee, J., Viollet, B., Xia, L., Zhang, Y. and Zou, M.-H. (2012) Activation of AMP-activated protein kinase α2 by nicotine instigates formation of abdominal aortic aneurysms in mice in vivo, nature medicine.
- Sonesson, B., Hansen, F. and Länne, T. (1997) Abdominal aortic aneurysm: A general defect in the vasculature with focal manifestations in the abdominal aorta? Journal of Vascular Surgery, 26, 247-254. doi:10.1016/S0741-5214(97)70185-X
- Schermerhorn, M.L., O’Malley, A.J., Jhaveri, A., Cotterill, P., Pomposelli, F. and Landon, B.E. (2008) Endovascular vs. open repair of abdominal aortic aneurysms in the Medicare population. The New England Journal of Medicine, 358, 464-474. doi:10.1056/NEJMoa0707348
- Sethi, K.V., Henry, A.J., Hevelone, N.D., Lipsitz, S.R., Belkin, M. and Nguyen, L.L. (2013) Impact of hospital market competition on endovascular aneurysm repair adoption and outcomes. Journal of Vascular Surgery.
- Smit, J.G.M. and Van Marle, J. (2012) Repair of abdominal aortic aneurysms with aorto-uni-iliac stentgraft and femoro-femoral bypass. South African Journal of Surgery, 50, 33-36.
- Cochennec, F., Becquemin, J.P., Desgranges, P., Allaire, E., Kobeiter, H. and Roudot-Thoraval, F. (2007) Limb graft occlusion following EVAR: Clinical pattern, outcomes and predictive factors of occurrence, European Journal of Vascular and Endovascular Surgery, 34, 59- 65. doi:10.1016/j.ejvs.2007.01.009
- Walraevens, J., Willaert, B., De Win, G., Ranftl, A., De Schutter, J. and Sloten, J.V. (2008) Correlation between compression, tensile and tearing tests on healthy and calcified aortic tissues. Medical Engineering & Physics, 30, 1098-1104. doi:10.1016/j.medengphy.2008.01.006
- Antoniou, G.A., Georgiadis, G.S., Antoniou, S.A., Kuhan G. and Murray, D. (2013) A meta-analysis of outcomes of endovascular abdominal aortic aneurysm repair in patients with hostile and friendly neck anatomy. Journal of Vascular Surgery, 57, 527-538. doi:10.1016/j.jvs.2012.09.050
- White, G.H., Yu, W., May, J., Chaufour, X. and Stephen, M.S. (1997) Endoleak as a complication of endoluminal grafting of abdominal aortic aneurysms: classification, incidence, diagnosis,and management. Journal of Endovascular Surgery, 4, 152-168. doi:10.1583/1074-6218(1997)004<0152:EAACOE>2.0.CO;2
- Chakfé, N., Dieval, F., Riepe, G., Mathieu, D., Zbali, I., Thaveau, F., Heintz, C., Kretz, J.-G. and Durand, B. (2004) Influence of the textile structure on the degradation of explanted aortic endoprostheses. European Journal of Vascular and Endovascular Surgery, 27, 33-41. doi:10.1583/1074-6218(1997)004<0152:EAACOE>2.0.CO;2
- Jacobs, T., Teodorescu, V., Morrissey, N., Carroccio, A., Ellozy, S., Minor, M., Hollier, L.H. and Marin, M.L. (2003) The endovascular repair of abdominal aortic aneurysm: An update analysis of structural failure modes of endovascular stent grafts. Seminars in Vascular Surgery, 16, 103-112. doi:10.1016/S0895-7967(03)00006-1
- De Bruin, J.L., Baas, A.F., Buth, J., Prinssen, M., Verhoeven, E.L.G., Cuypers, P.W.M., van Sambeek, M.R.H. M., Balm, R., Grobbee, D.E. and Blankensteijn, J.D. (2010) Long-term outcome of open or endovascular repair of abdominal aortic aneurysm. The New England Journal of Medicine, 362, 1881-1889. doi:10.1056/NEJMoa0909499
- Amblard, A. (2006) Contribution à l’étude du comportement d’une endoprothèse aortique abdominale: Analyse des endofuites de type I. Ph.D. Thesis, INSA-LYON.
- Son, B.-S., Chung, S.W., Lee, C., Ahn, H.Y., Kim, S. and Kim, C.W. (2011) Clinical efficacy of endovascular abdominal aortic aneurysm repair. The Korean Journal of Thoracic and Cardiovascular Surgery, 44, 142.
- Khanna, N. (2011) Endovascular repair of thoracic and abdominal aortic aneurysms/dissections. Apollo Medicine, 8, 217-227. doi:10.1016/S0976-0016(11)60077-X
- Kato, N., Dake, M.D., Semba, C.P., Razavi, M.K., Kee, S.T., Slonim, S.M., Samuels, S.L., Terasaki, K.K., Zarins, C.K., Mitchell, R.S. and Miller, D.C. (1998) Treatment of aortoiliac aneurysms with use of single-piece tapered stent-grafts. Journal of Vascular and Interventional Radiology, 9, 41-49.
- Willaert, W.I.M., Aggarwal, R., Van Herzeele, I., O’Donoghue, K., Gaines, P.A., Darzi, A.W., Vermassen, F.E. and Cheshire, N.J. (2011) Patient-specific endovascular simulation influences interventionalists performing carotid artery stenting procedures. European Journal of Vascular and Endovascular Surgery, 41, 492-500. doi:10.1016/j.ejvs.2010.12.013
- Treyve, F., Ohayon, J., Finet, G. and Rioufol, G. (2003) Modelling of the stress distribution in an artherosclerotic plaque in man using a Finite Element Analysis. Comptes Rendus Mecanique, 331, 449-454. doi:10.1016/S1631-0721(03)00089-5
- Li, Z.-Y., Howarth, S., Trivedi, R.A., U-King-Im, J.M., Graves, M.J., Brown, A., Wang, L. and Gillard, J.H. (2006) Stress analysis of carotid plaque rupture based on in vivo high resolution MRI. Journal of Biomechanics, 39, 2611-2622. doi:10.1016/j.jbiomech.2005.08.022
- Páez, J.M.G., Carrera, A., Jorge, E., Millán, I., Cordon, A., Maestro, M.A., Rocha, A. and Castillo-Olivares, J.L. (2004) Resistance to tearing of calf and ostrich pericardium: Influence of the type of suture material and the direction of the suture line. Journal of Biomedical Materials Research Part B: Applied Biomaterials, 69, 125-134. doi:10.1002/jbm.b.20014
- Martinez, A.W. and Chaikof, E.L. (2011) Microfabrication and nanotechnology in stent design. Wiley Interdiscplinary Reviews: Nanomedicine and Nanobiotechnology, 3, 256-268. doi:10.1002/wnan.123
- Walraevens, J., Willaert, B., De Win, G., Ranftl, A., De Schutter, J. and Sloten, J.V. (2008) Correlation between compression, tensile and tearing tests on healthy and calcified aortic tissues. Medical Engineering & Physics, 30, 1098-1104. doi:10.1016/j.medengphy.2008.01.006
- Dimitriadis, E.K., Horkay, F., Maresca, J., Kachar, B. and Chadwick, R.S. (2002) Determination of Elastic Moduli of Thin Layers of soft material using the atomic force microscope. Biophysical Journal, 82, 2798-2810. doi:10.1016/S0006-3495(02)75620-8
- Neumann, T. Determination the elastic modulus of biological samples using atomic microscope. JPK Instruments, Nanowizard.
- Sun, J.S., Lee, K.H. and Lee, H.P. (2000) Comparison of implicit and explicit finite element methods for dynamic problems. Journal of Materials Processing Technology, 105, 110-118. doi:10.1016/S0924-0136(00)00580-X
- Harewood, F.J. and McHugh, P.E. (2007) Comparison of the implicit and explicit finite element methods using crystal plasticity. Computational Materials Science, 39, 481-494. doi:10.1016/S0924-0136(00)00580-X
- Hughes, T. (1987) The finite element method—Linear static and dynamic, finite element analysis. Prentice Hall, Inc.
- Cook, R.D., Malkus, D.S., Plesha, M.E. and Witt, R.J. (2002) Concepts and applications of finite element analysis. 4th Edition, John Wiley & Sons, New York, 719.
- Holzapfel, G.A. and Gasser, T.C. (2001) A viscoelastic model for fiber-reinforced composites at finite strains: Continuum basis, computational aspects and applications, Computer Methods in Applied Mechanics and Engineering, 190, 4379-4403. doi:10.1016/S0045-7825(00)00323-6
- Saini, A., Berry, C. and Greenwald, S. (1995) Effect of age and sex on residual stress in the aorta. Journal of Vascular Research, 32, 398-405.
- Hong, M.K., Vossoughi, J., Mintz, G.S., Kauffman, R.D., Hoyt, R.F., Cornhill, J.F., Herderick, E.E., Leon, M.B. and Hoeg, J.M. (1997) Altered compliance and residual strain precede angiographically detectable early atherosclerosis in low-density lipoprotein receptor deficiency. Arteriosclerosis, Thrombosis, and Vascular Biology, 17, 2209-2217.

