Journal of Biomedical Science and Engineering
Vol. 5 No. 11 (2012) , Article ID: 24768 , 8 pages DOI:10.4236/jbise.2012.511083
Biomechanical prediction of abdominal aortic aneurysm rupture risk: Sensitivity analysis
![]()
1Department of Mechanical and Materials Engineering, University of Nebraska-Lincoln, Lincoln, USA
2Nebraska Center for Materials and Nanoscience, Lincoln, USA
Email: *lgu2@unl.edu
Received 30 July 2012; revised 13 September 2012; accepted 20 September 2012
Keywords: Abdominal Aortic Aneurysm (AAA); Response Surface Method; Central Composite Design (CCD); Regression; Peak Wall Stress; Finite Element Analysis (FEA)
ABSTRACT
Objectives: The purpose of this research is to determine the quantitative relationship between the peak wall stress of abdominal aortic aneurysm (AAA) and its clinical risk factors including its maximum diameter, asymmetry index, wall thickness and abnormal high blood pressure. Methods: The response surface experimental design with one response and four variables was used to design the experimental tests. Thirty experiments were performed through finite element analysis in order to obtain the designed response values. Results: A nonlinear multivariable regression function was developed based on the experimental data. Results demonstrated the inefficiency of traditional 5-cm criterion for estimating the rupture of AAA. The profound effect of wall thickness on the peak wall stress has been observed and validated by the existing publications. Conclusion: The conventional 5-cm criterion for estimating AAA rupture might induce biased prediction, and multiple clinical risk factors need to be considered in realistic clinical settings.
1. INTRODUCTION
Abdominal aortic aneurysm (AAA) rupture led to a mortality rate of 90%, which was rated as the 13th most common cause of death in US [1]. The mechanism of AAA rupture has not been fully understood. In clinical practice, the maximum diameter of the aneurysm larger than 5 cm is used as the criterion for deciding the elective repair of AAA [2]. However, clinical studies showed that this 5- cm diameter criterion might cause late decision of repair at least for a certain group of patients [2]. Darling et al. reported a rupture rate of 12.8% for AAAs with a maximum diameter less than 5 cm and 40% for AAAs with a diameter larger than 5 cm in an autopsy study [3]. Hall et al. observed that the rupture rate for AAAs with a maximum diameter less than 5 cm could be up to 23% [4].
The high mortality associated with the AAA rupture and the inaccuracy of the traditional 5-cm criterion need improved surgical decision criterion to predict the AAA rupture risk [2,5]. From the biomechanical standpoint, the rupture of AAA was initiated when the local mechanical stress on the aneurysm exceeds the failure strength of the local material [6]. Therefore, the mechanical stress of AAAs might serve as a criterion to predict or decide the AAA rupture [7]. Vorp et al. have investigated the relationship between the mechanical stress in AAAs and the factors of maximum diameter and asymmetric bulge through three-dimensional computational models in 1998 [8]. Since then, many experimental and computational studies have been conducted to investigate the effects of other characteristics of aneurysm on its mechanical stress, such as the thickness of aneurysm wall [5,9-11], the properties of material [12], and hypertension [13]. Although different mechanical variables leading to AAA rupture have been presented in the literature, the sensitivity analysis of these variables in determining the peak mechanical stress is lacking.
In this work, four different clinical risk factors of AAA, i.e. maximum diameter, asymmetry index, wall thickness and abnormal high blood pressure, were used to quantify the uncertainty in determining the peak wall stress through statistical modeling. A relationship between multiple inputs and the resulted peak wall stress of AAA was developed, which could be used to enhance the quantification or understanding of AAA rupture potential and its sensitivity to various risk factors.
2. MATERIALS AND METHODS
2.1. Experiment Design
A multivariate experimental design, referred to as response surface methodology (RSM), was adopted to investigate the relationship between an array of experimental factors under control and the measured response. One specific RSM, i.e., the central composite design (CCD), was used to build a quadratic polynomial model for the response variables. The four independent variables, including maximum diameter, wall thickness, asymmetry index of AAA shape, and abnormal high blood pressure, were chosen based on the previous publications [2,7,8,14]. The response variable was targeted as peak wall stress of AAA. Considering the classical 5-cm diameter criterion, the maximum diameter of AAA ranging from 3 to 6 cm was used for the sensitivity tests. Since the traditional hypertension threshold is 140 mmHg (18.6 KPa) [15], the input range of high blood pressure was chosen between 120 mmHg (15.9 KPa) and 160 mmHg (21.3 KPa) to include the quasi-hypertension as well. The asymmetry index of AAA, defined as the ratio of maximum posterior wall dimension rp to maximum anterior wall dimension ra as shown in Figure 1 [8], has a range from 0.3 to 1; while the wall thickness of AAA varies from 0.8 mm to 2.2 mm. When constructing the CCD, these natural variables are usually transformed into dimensionless coded variables.
For a CCD, the observations were first divided into two blocks: a factorial-points block which is composed of nf factorial points and n0f center points, and an axialpoints block composed of na axial points and n0a center points [16]. Figure 2 shows the scheme of CCD with two independent variables. Thus, the total number of experiments in a CCD will be . In the factorial design, each factor has the minimum number of levels, i.e. two levels. In these designs, +1 and −1 are usually used to denote the high and low level of each factor. For a full factorial design with k = 4 variables, there are total
. In the factorial design, each factor has the minimum number of levels, i.e. two levels. In these designs, +1 and −1 are usually used to denote the high and low level of each factor. For a full factorial design with k = 4 variables, there are total 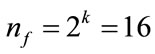 factorial points in this work. The axial points represent the tests where all factors except one are set at their mid-levels; thus, there are total
factorial points in this work. The axial points represent the tests where all factors except one are set at their mid-levels; thus, there are total
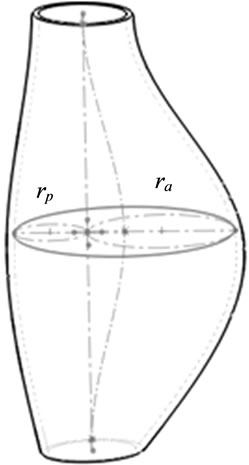
Figure 1. The 3-D solid model of AAA.
 axial points in this work. The distance between the axial points and center point is denoted by
axial points in this work. The distance between the axial points and center point is denoted by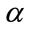 , which is defined based on coded values. Rotatability, which ensures the variance of the predicted responses rely solely on the distance from observation point to the center point (in terms of the coded variables), is one desirable property of CCD [16]. As for the choice of
, which is defined based on coded values. Rotatability, which ensures the variance of the predicted responses rely solely on the distance from observation point to the center point (in terms of the coded variables), is one desirable property of CCD [16]. As for the choice of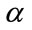 , the formula
, the formula 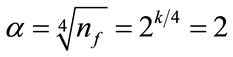 was used in order to guarantee the rotatability. These levels for the independent variables given in Table 1 are also used to establish the limits (ranges) for the optimization process of the objective quadratic polynomial function described below. As a rough guide line, approximately 3 to 5 center points should be added to the full factorial design, and n0f = 4 was the default value chosen by the software. For rotatability, the center points in both blocks should satisfy
was used in order to guarantee the rotatability. These levels for the independent variables given in Table 1 are also used to establish the limits (ranges) for the optimization process of the objective quadratic polynomial function described below. As a rough guide line, approximately 3 to 5 center points should be added to the full factorial design, and n0f = 4 was the default value chosen by the software. For rotatability, the center points in both blocks should satisfy
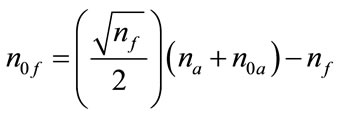 [16]. The relationship as n0f
[16]. The relationship as n0f
= 2n0a was obtained by substituting all actual numbers into the formula above. Thus, there are n0a = 2 axial center points. In summary, the completed experimental design in this work involves a total of 30 observations with 16 factorial points and 4 factorial center points, 8 axial points and 2 axial center points, as listed in Table 2.
The response variable of the CCD could be expressed as the following second-order polynomial equation using a multiple regression technique
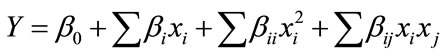 (1)
(1)
where Y represents the predicted response (Herein, it is peak wall stress), xi and xj denote the input variables using coded values, as listed in Table 1; β0 is the intercept
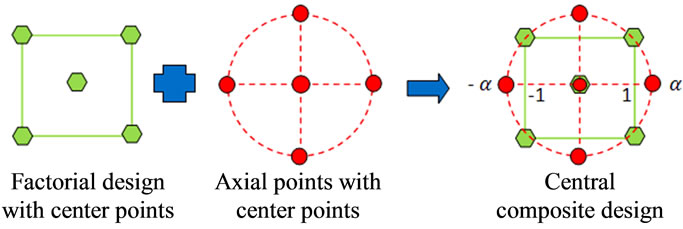
Figure 2. The design scheme of CCD with two variables [17].

Table 1. Coded factors and their corresponding actual values.
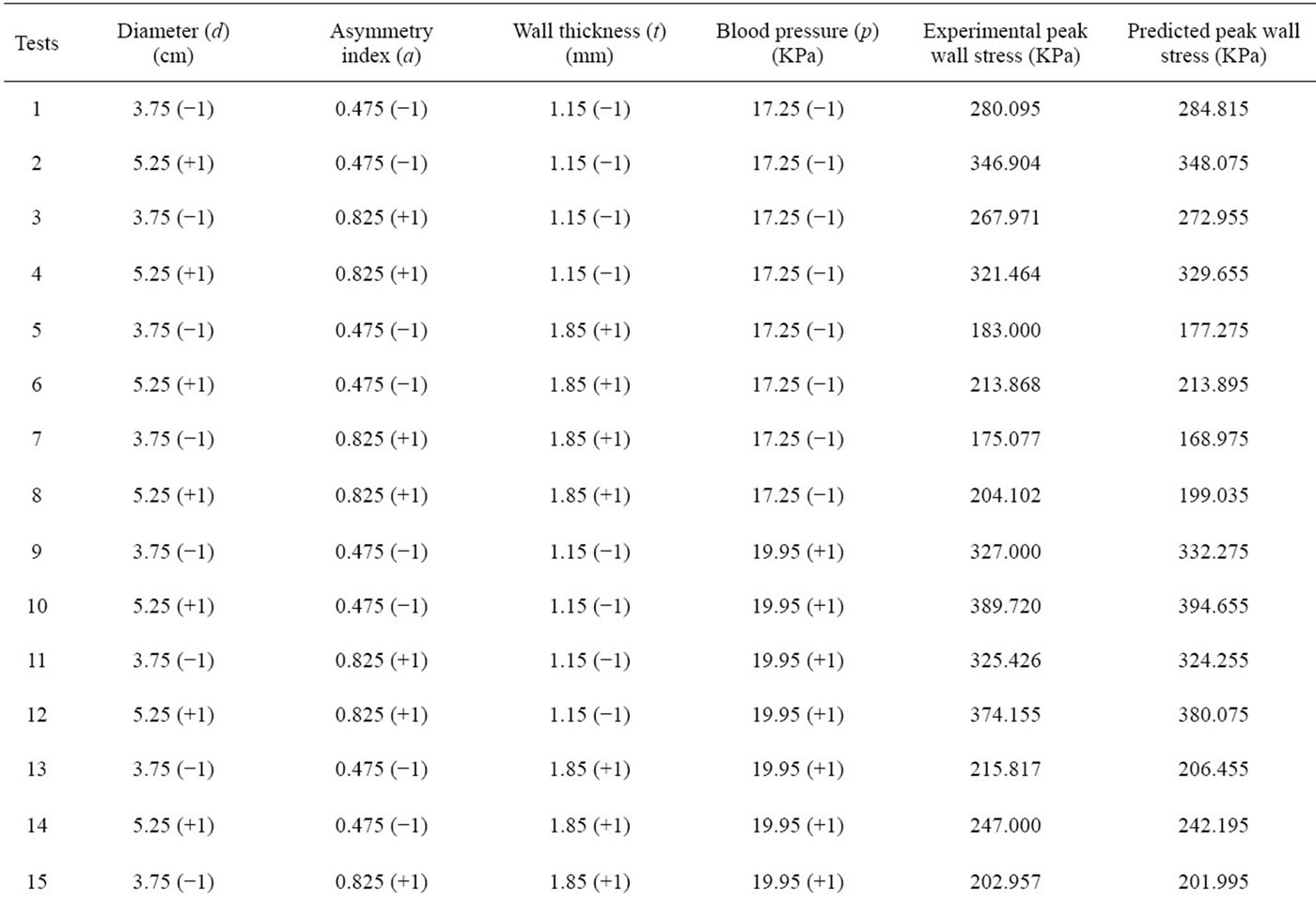
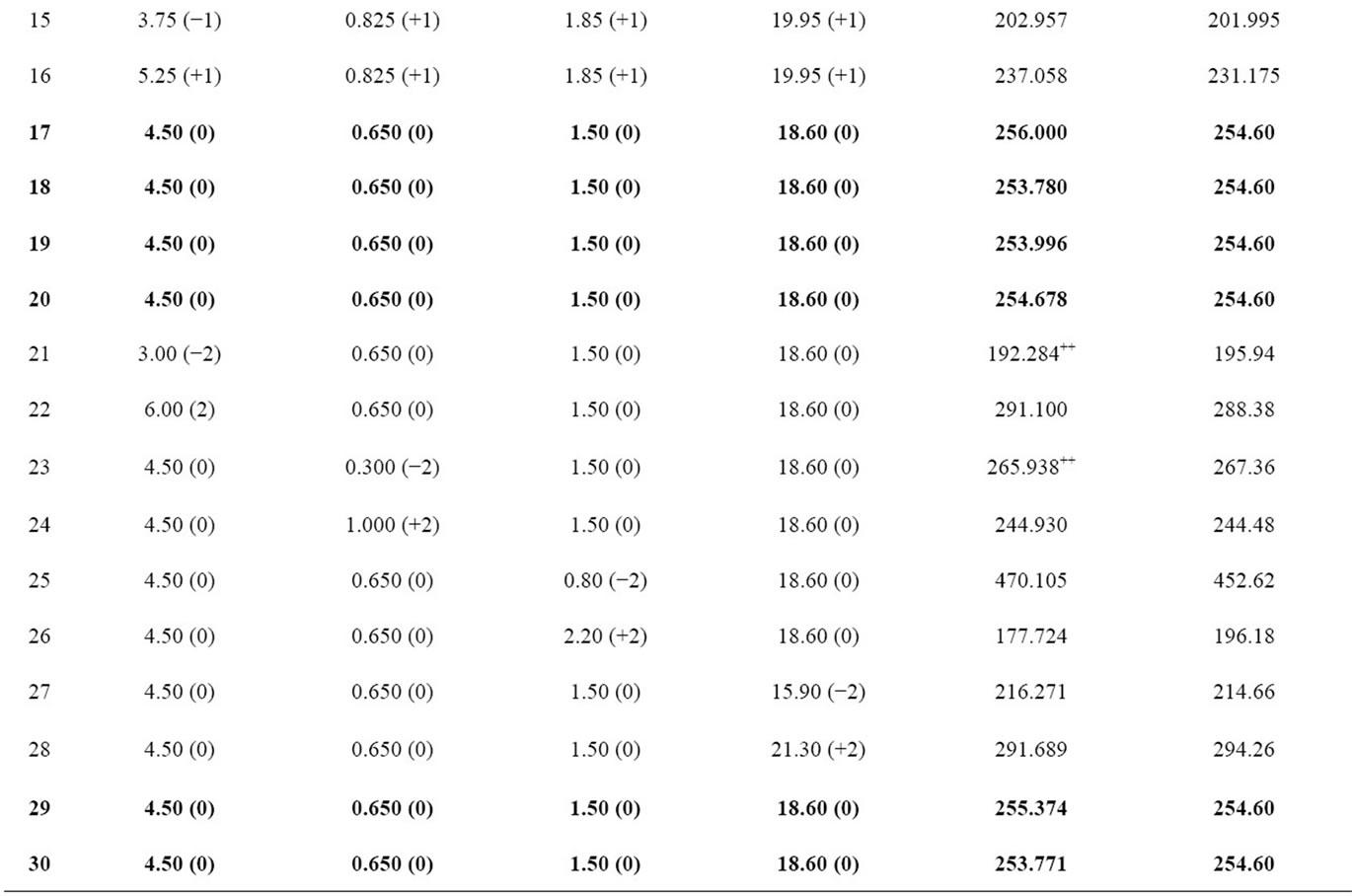
Table 2. The design matrix of the CCD and the corresponding experimental response data as well as predicted response data.
term, which is constant; βi quantify the linear effect of each factor; βii quantify the quadratic effect of each factor; βij quantify the interactive effects between two different factors [16].
Experimental designs and the polynomial coefficients were calculated and analyzed using a trial version of MiniTAB software-version 12.0 (Minitab Inc., state college, PA, USA). Statistical analysis of the model was performed to evaluate the analysis of variance (ANOVA).
2.2. Finite Element Model
The predicted response in this work is the peak wall stress of the AAA, and the finite element method was adopted to calculate the corresponding peak wall stress in each experimental test. The shape of the AAA at the central portion was controlled by the maximum diameter and the asymmetry index. In all 30 experimental tests listed in Table 2, there are 9 (4 for factorial design, 4 for axial points and 1 for central points) different geometrical models of AAA in total, which were developed in Solidworks 2011 (Dassault Systèmes SolidWorks Corp., Concord, MA, USA). As marked in Figure 1, the maximum inner diameter d = rp + ra, where the rp and ra were maximum posterior and anterior wall dimensions, respectively; and the asymmetry index β = rp/ra [8]. The axial length of AAA and its diameter at both ends were set as 120 mm and 20 mm, respectively. The wall thickness of aneurysm vessel was assumed uniform. The mechanical properties of the aneurysm wall is described with hyperelastic material model, and the second-order Mooney-Rivlin strain energy function was used
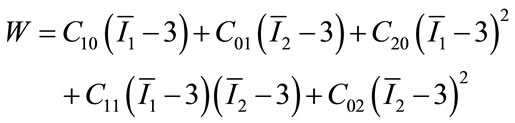 (2)
(2)
where C10, C01, C20, C11, C02 are material coefficients. Based on the published uniaxial tensile test data of AAA specimen [18], the non-zero coefficients C10 = −0.60908 MPa, C01 = 1.12033 MPa, C20 = −3.06279 MPa, C11 = 2.12802 MPa, C02 = 0.93689 MPa were adopted. As for the boundary conditions, the displacements along all directions at two ends were constrained, and the blood pressure was applied onto the inner wall of AAA uniformly.
3. RESULTS AND DISCUSSIONS
In order to investigate the linear, quadratic and interacttive influence of four risk factors related to AAA (maximum diameter, asymmetry index, wall thickness and abnormal high blood pressure) on its peak wall stress and optimize the coefficients, 30 experimental tests were required for four-factor CCD. The experimental design matrix and corresponding levels of the variables are shown in Table 2. The response (i.e. peak wall stress) was obtained by conducting finite element analysis on each experimental test, and all values related to each experimental test were listed in Table 2.
The analysis of variance (ANOVA) was performed to statistically evaluate the model, as shown in Table 3. The coefficient of determination R2 of the model was 0.9916, indicating that 99.16% variation in the peak wall stress of AAA could be explained by the statistical model. The p value for linear term and square term is 0.015 and 0.000, respectively. Both of them are less than 0.05, confirming the applicability of the model. According to the F test of ANOVA, the obtained quadratic regression function was significant (p < 0.05), indicating that the peak wall stress of AAA has a strong relationship with the selected four risk factors [19]. An insignificant lackof-fit (p > 0.05) indicates the goodness of the proposed model when fitting the data [20]. However, the lack-offit in this work was biased towards the side of signifycance (p < 0.05), this could be explained by the duplication of the central point tests due to the ideality of the computer simulation, which are not true replication of the experiment.
Based on the peak Von Mises stress on the wall of AAA (Table 2), which serve as the predicted response, the multi-variables regression analysis was performed using MiniTAB to obtain the quadratic response surface model and second-order equation was fitted as
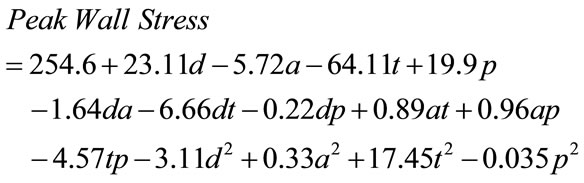 (3)
(3)
where a, d, p, and t are coded variables for asymmetry index, maximum diameter, abnormal high blood pressure, and wall thickness, respectively. The histogram of the residuals for all observations, which were calculated as the difference between the experimental value and the
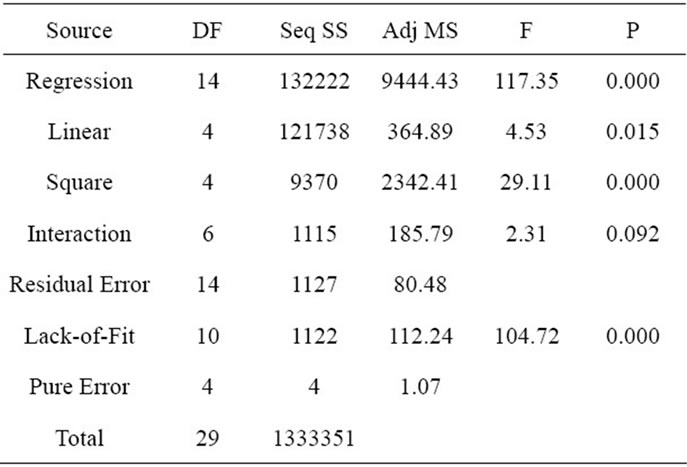
Table 3. ANOVA of the regression function.
predicted value from the regression model, was plotted in Figure 3. As can be seen, the histogram exhibited as approximate bell-shape, indicating the approximate normal distribution of the residuals. All residuals were found to fall in the range from −20 KPa to 20 KPa.
The comparison of stress distribution between two geometry models with diameters larger or less than 5 cm was shown in Figure 4. As can be seen, the peak wall stress in experimental test 2 was 346.9 KPa, while it is 470.1 KPa in experimental test 21. The corresponding maximum diameter in experimental test 2 is 5.25 cm, and it is 3.0 cm in experimental test 21, indicating the inadequacy of 5-cm criterion in predicting the rupture of AAA. In addition to the magnitude of the peak wall stress, their locations mainly concentrate on the posterior side in both cases, especially when the asymmetry of AAAs was patent (like experimental test 2). It indicates the correlation between potential rupture of AAA and the geometrical asymmetry of AAA. This statement keeps consistent with the conclusion achieved by Vorp et al., who investigated the relationship between the peak wall stress of AAA and asymmetry using ideal model, and concluded that stress and potential rupture were dependent on the asymmetric shape of AAA [8].
The regression model in this work showed that the peak wall stress on AAA is determined by multiple risk factors. The contribution of each risk factor to the response was determined based on the absolute value of coefficients at first order, and the sequence was wall thickness, maximum diameter, abnormal high blood pressure, and asymmetry index. The profound effect of wall thickness on the magnitude and location of peak wall stress has been confirmed by Xiong et al., though the stress pattern was least affected [21]. A contour plot, the projection of the response surface onto a two-dimensional plane, will illustrate the impact of variables and
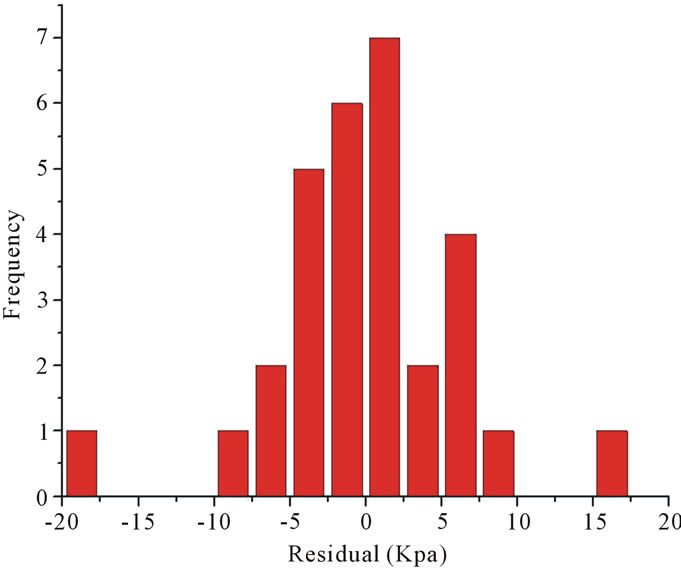
Figure 3. The histogram of residuals.
 (a)
(a)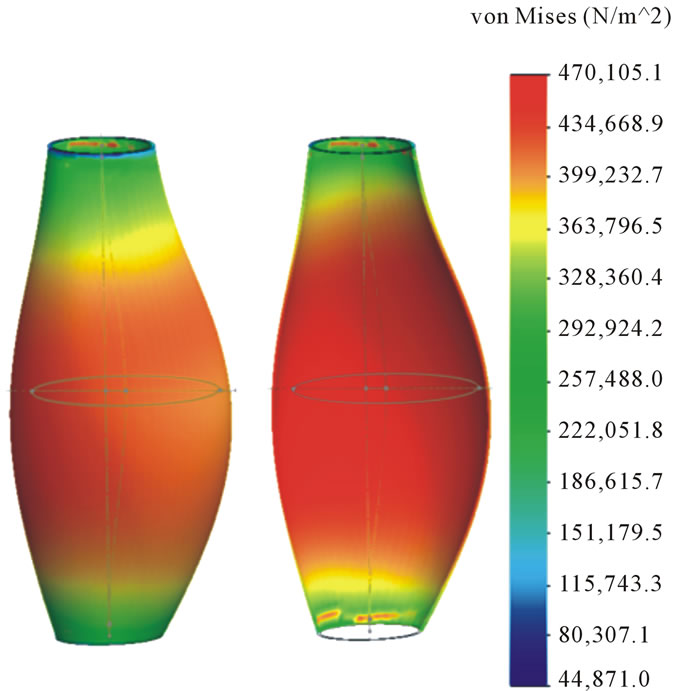 (b)
(b)
Figure 4. Comparison of wall stress distribution of AAA. (a) Experimental test 2; (b) Experimental test 21.
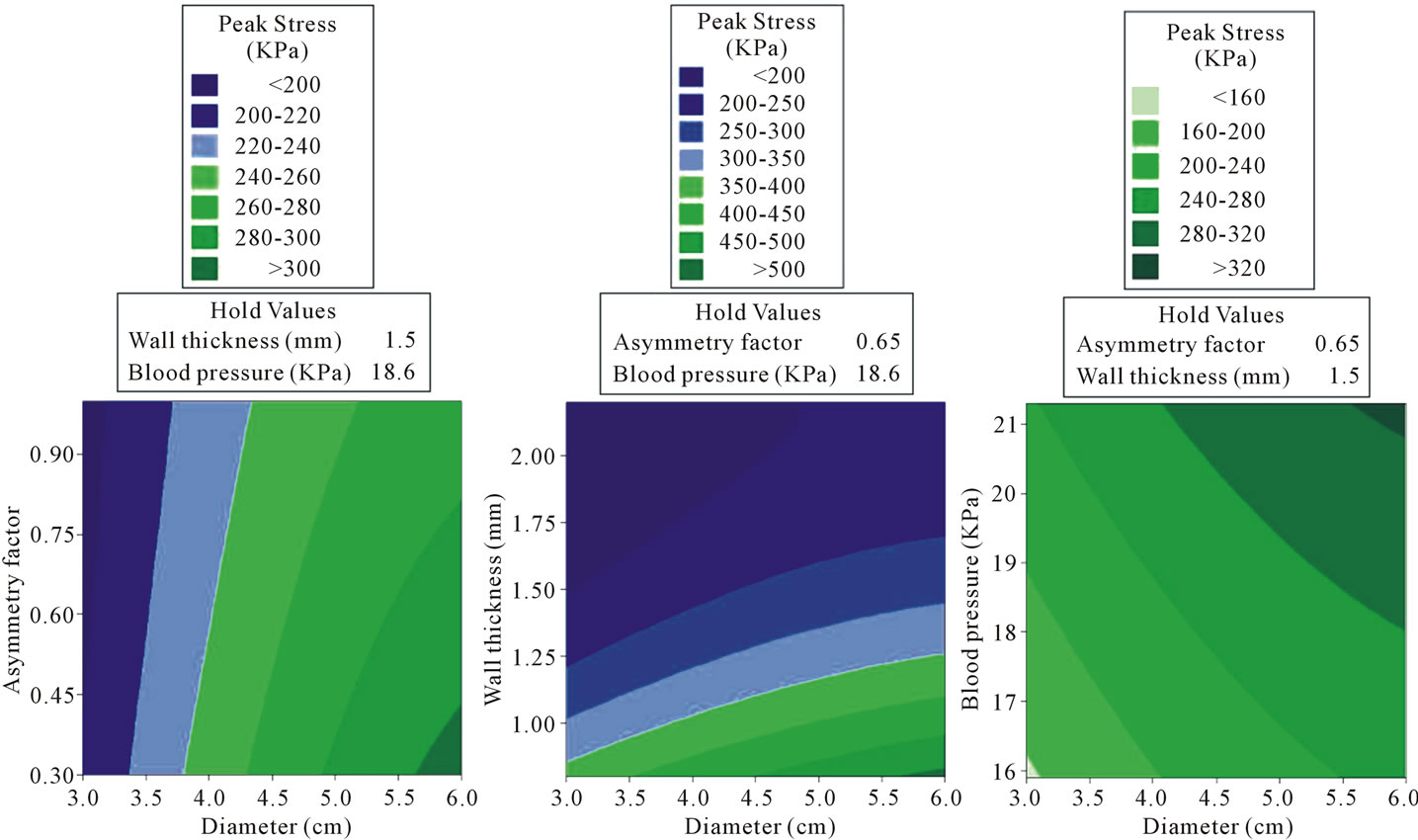
their interaction on the response [22]. In order to better understand the influence of the variables, especially the maximum diameter of AAA, the contour plots between the response (i.e. the peak wall stress) and the combined effects of maximum diameter and each of other three variables (i.e. asymmetric index, wall thickness, and blood pressure) were drawn, as shown in Figure 5. The figure shows that the peak wall stress increased with the increment in maximum diameter and blood pressure, decreased with the increment in asymmetry index and
 (a) (b) (c)
(a) (b) (c)
Figure 5. The contour plots of (a) the asymmetry factor and maximum diameter of AAA (cm); (b) the wall thickness (mm) and maximum diameter of AAA (cm); (c) the blood pressure (KPa) and maximum diameter of AAA (cm) on peak wall stress (KPa).
wall thickness. However, larger maximum diameter of AAA does not always lead to larger peak wall stress. Given that the asymmetry index is 0.3, the wall thickness is 0.8 mm and the blood pressure of hypertension is 21.3 KPa, the smallest maximum diameter of AAA in this work (3 cm) will lead to a peak wall stress of 432.06 KPa based on the obtained regression function. It is larger than the peak wall stress (291.1 KPa) obtained from the only experimental test when the maximum diameter of AAA is 6 cm. All of the considerations discussed above suggest that the prediction of potential rupture of AAAs based on the single factor of maximum diameter will be biased and the Law of Laplace has limitations in predicting the rupture of AAAs. Because the Law of Laplace usually assumes the wall stress is proportional to the diameter [11]; however, it may not be valid for complex geometrical features of the AAA walls [11,23]. The obtained regression function demonstrates the multivariate effects on peak wall stress, which is consistent with other previous observations [2].
In addition to the criterion of AAA rupture, the rupture location is also the area of interests. According to the clinical statistics, nearly 80% of all AAA ruptures are located in the posterior of AAAs [24]. The explanation is that the existence of spinal column constrains the posterior side and makes it expand only along the anterior direction, causing the stress concentrates in the posterior location [25]. This has been shown by Raghavan et al. through studying a large number of AAA rupture cases [24]. However, the presence of spinal column was not considered in this work, which will be incorporated in future works. Therefore, it was not reasonable to explain this phenomenon using the influence of spinal column. Through comparing the geometries between the posterior side and anterior side of AAA, we found that both the area and curvature of the posterior side were smaller than those of the anterior side. Under the boundary conditions of fixing two ends and loading conditions of uniform blood pressure, the stress on the AAA wall, especially the major stress component-circumferential stress, is proportional to the local radius of curvature. The smaller local curvature of the posterior side is reasonable to induce larger stress. As a result, more rupture cases often appeared in the posterior side other than the anterior side.
4. CONCLUSION
In this work, a methodology integrating experiment design and nonlinear regression was used to investigate the impacts of four risk factors on potential AAA rupture. The obtained regression function was used to illustrate the inefficiency of traditional 5-cm criterion for estimating the AAA rupture. Even though the material of AAA exhibits heterogeneity and anisotropy in-vivo, homogeneous and isotropic material properties were assigned to govern the mechanical response of the AAA wall. The solid model of AAA was simplified and idealized for this comparative study; the stress distribution and the resulted peak wall stress would exhibit wide variations on patient-specific models [26]. Constant blood pressure was applied to the inner wall of AAA and a fluid-structure interaction detail will provide more accurate stress estimation [27,28]. Despite these simplifications, the present work demonstrated the detailed biomechanics of AAA as well as its sensitivity to various factors. The developed regression model in this work is more convenient to be used in clinical settings.
![]()
![]()
REFERENCES
- Patel, M.I., Hardman, D.T., Fisher, C.M. and Appleberg, M. (1995) Current views on the pathogenesis of abdominal aortic aneurysms. Journal of the American College Surgeons, 181, 371-382.
- Vorp, D.A. and Vande Geest, J.P. (2005) Biomechanical determinants of abdominal aortic aneurysm rupture. Arteriosclerosis, Thrombosis, and Vascular Biology, 25, 1558- 1566. doi:10.1161/01.ATV.0000174129.77391.55
- Darling, R.C., Messina, C.R., Brewster, D.C. and Ottinger, L.W. (1977) Autopsy study of unoperated abdominal aortic aneurysms. The case for early resection. Circulation, 56, 161-164.
- Hall, A.J., Busse, E.F., McCarville, D.J. and Burgess, J.J. (2000) Aortic wall tension as a predictive factor for abdominal aortic aneurysm rupture: Improving the selection of patients for abdominal aortic aneurysm repair. Annals of Vascular Surgery, 14, 152-157. doi:10.1007/s100169910027
- Doyle, B.J., Callanan, A., Burke, P.E., Grace, P.A., Walsh, M.T., Vorp, D.A. and McGloughlin, T.M. (2009) Vessel asymmetry as an additional diagnostic tool in the assessment of abdominal aortic aneurysms. Journal of Vascular Surgery, 49, 443-454. doi:10.1016/j.jvs.2008.08.064
- Truijers, M., Pol, J.A., Schultzekool, L.J., Van Sterkenburg, S.M., Fillinger, M.F. and Blankensteijn, J.D. (2007) Wall stress analysis in small asymptomatic, symptomatic and ruptured abdominal aortic aneurysms. European Journal of Vascular & Endovascular Surgery, 33, 401-407. doi:10.1016/j.ejvs.2006.10.009
- Kleinstreuer, C. and Li, Z. (2006) Analysis and computer program for rupture-risk prediction of abdominal aortic aneurysms. Biomedical Engineering Online, 5, 19. doi:10.1186/1475-925X-5-19
- Vorp, D.A., Raghavan, M.L. and Webster, M.W. (1998) Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry. Journal of Vascular Surgery, 27, 632-639. doi:10.1016/S0741-5214(98)70227-7
- Adolph, R., Vorp, D.A., Steed, D.L., Webster, M.W., Kameneva, M.V. and Watkins, S.C. (1997) Cellular content and permeability of intraluminal thrombus in abdominal aortic aneurysm. Journal of Vascular Surgery, 25, 916-926. doi:10.1016/S0741-5214(97)70223-4
- Raghavan, M.L., Kratzberg, J., Castro de Tolosa, E.M., Hanaoka, M.M., Walker, P. and Da Silva, E.S. (2006) Regional distribution of wall thickness and failure properties of human abdominal aortic aneurysm. Journal of Biomechanics, 39, 3010-3016. doi:10.1016/j.jbiomech.2005.10.021
- Vorp, D.A. (2007) Biomechanics of abdominal aortic aneurysm. Journal of Biomechanics, 40, 1887-1902. doi:10.1016/j.jbiomech.2006.09.003
- Rodriguez, J.F., Ruiz, C., Doblare, M. and Holzapfel, G.A. (2008) Mechanical stresses in abdominal aortic aneurysms: Influence of diameter, asymmetry, and material anisotropy. Journal of Biomechanical Engineering, 130, 021023-021032. doi:10.1115/1.2898830
- Helderman, F., Manoch, I.J., Breeuwer, M., Kose, U., Boersma, H., Van Sambeek, M.R.H.M., Pattynama, P.M.T., Schouten, O., Poldermans, D., Wisselink, W., Van der Steen, A.F. and Krams, R. (2010) Predicting patient-specific expansion of abdominal aortic aneurysms. European Journal of Vascular & Endovascular Surgery, 40, 47-53. doi:10.1016/j.ejvs.2010.02.017
- Raghavan, M.L., Kratzberg, J. and Da Silva, E.S. (2004) Heterogeneous, variable wall-thickness modeling of a ruptured abdominal aortic aneurysm. Proceedings of the ASME International Mechanical Engineering Conference, 13-19 November 2004, Anaheim, 271-272.
- Port, S., Demer, L., Jennrich, R., Walter, D. and Garfinkel, A. (2000) Systolic blood pressure and mortality. Lancet, 355, 175-180. doi:10.1016/S0140-6736(99)07051-8
- Dean, A. and Voss, D. (1999) Design and analysis of experiments. Springer, New York. doi:10.1007/b97673
- Lee, B.-H., Hong, J.-P. and Lee, J.-H. (2012) Optimum design criteria for maximum torque and efficiency of a line-start permanent-magnet motor using response surface methodology and finite element method,” IEEE Transactions on Magnetics, 48, 863-866.
- Xiong, J., Wang, S.M., Zhou, W. and Wu, J.G. (2008) Measurement and analysis of ultimate mechanical properties, stress-strain curve fit, and elastic modulus formula of human abdominal aortic aneurysm and nonaneurysmal abdominal aorta. Journal of Vascular Surgery, 48, 189- 195. doi:10.1016/j.jvs.2007.12.053
- Vaikousi, H. and Biliaderis, C.G. (2005) Processing and formulation effects on rheological behavior of barley betaglucan aqueous dispersions. Food Chemistry, 91, 505-516. doi:10.1016/j.foodchem.2004.04.042
- Montgomery, D.C. (2003) Design and analysis of experiments. John Wiley & Sons, Singapore.
- Xiong, J., Guo, W., Wang, J. and Zhou, W. (2009) Effects of Wall Thickness on Stress Distribution in PatientSpecific Models of Abdominal Aortic Aneurysm. Proceedings of the 2nd International Conference on Biomedical Engineering and Informatics, 17-19 October 2009, Tianjin, 1-3.
- Hasan, S.H., Srivastava, P., Ranjan, D. and Talat, M. (2009) Biosorption of Cr(VI) from aqueous solution using A. hydrophila in up-flow column: Optimization of process variables. Applied Microbiology and Biotechnology, 83, 567-577. doi:10.1007/s00253-009-1984-x
- Georgakarakos, E., Ioannou, C.V., Papaharilaou, Y., Kostas, T. and Katsamouris, A.N. (2011) Computational evaluation of aortic aneurysm rupture risk: What have we learned so far? Journal of Endovascular Therapy, 18, 214-225. doi:10.1583/10-3244.1
- Raghavan, M.L., Hanaoka, M.M., Kratzberg, J.A., De Lourdes Higuchi, M. and Da Silva, E.S. (2011) Biomechanical failure properties and microstructural content of ruptured and unruptured abdominal aortic aneurysms. Journal of Biomechanics, 44, 2501-2507. doi:10.1016/j.jbiomech.2011.06.004
- Papaharilaou, Y., Ekaterinaris, J.A., Manousaki, E. and Katsamouris, A.N. (2007) A decoupled fluid structure approach for estimating wall stress in abdominal aortic aneurysms. Journal of Biomechanics, 40, 367-377. doi:10.1016/j.jbiomech.2005.12.013
- Georgakarakos, E., Ioannou, C.V., Kamarianakis, Y., Papaharilaou, Y., Kostas, T., Manousaki, E. and Katsamouris, A.N. (2010) The role of geometric parameters in the prediction of abdominal aortic aneurysm wall stress. European Journal of Vascular & Endovascular Surgery, 39, 42-48. doi:10.1016/j.ejvs.2009.09.026
- Scotti, C.M., Shkolnik, A.D., Muluk, S.C. and Finol, E.A. (2005) Fluid-structure interaction in abdominal aortic aneurysms: Effects of asymmetry and wall thickness. Biomedical Engineering Online, 4, 64. doi:10.1186/1475-925X-4-64
- Xenos, M., Rambhia, S.H., Alemu, Y., Einav, S., Labropoulos, N., Tassiopoulos, A., Ricotta, J.J. and Bluestein, D. (2010) Patient-based abdominal aortic aneurysm rupture risk prediction with fluid structure interaction modeling. Annals of Biomedical Engineering, 38, 3323-3337. doi:10.1007/s10439-010-0094-3
NOTES
*Corresponding author.

