Natural Science
Vol.6 No.7(2014), Article ID:45359,4 pages DOI:10.4236/ns.2014.67051
Follow the Multitude—A Thermodynamic Approach
Oded Kafri
Varicom Communications Ltd., Tel Aviv, Israel
Email: oded@varicom.co.il
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 December 2013; revised 22 January 2014; accepted 29 January 2014
ABSTRACT
When a bit is added to a file, its entropy increases by one nat regardless of the length of the file or the value of the bit. However, when a node is added to a network, the entropy increase is a function of the ratio between the links and the nodes in the network. Therefore, the thermodynamic incentive for a node to join a highly linked network is higher than to join a poorly linked network.
Keywords
Information Theory, Networks, Entropy

1. Introduction
The propensity of networks to grow is a characteristic of life. It is observed in biological networks, i.e. blood vessels, neurons, fungus etc. It is also observed in sociological networks i.e. communities, companies, guilds, etc., and in man-made networks as electrical, transportation, communication etc. It seems that the crowded the network, the higher its tendency to grow. Here we argue that adding a node to a highly linked network generates more entropy than adding a node to a poorly linked network. Since the second law of thermodynamics states that entropy tends to increase to it maximum, we conclude that the second law yields higher incentive to a node to join to highly linked networks.
Networks and files are different from gases or solutions. However, from a statistical-mechanics point of view, any physical system comprises of particles, states and microstates. The particles may be atoms, molecules, links, energetic bits, etc., correspondently, states are the possible spatial locations, nodes, bits etc. and microstates are the possible different configurations of the particles in the states. It should be noted that sometimes the numbers of particles, states and microstates are a function of energy and/or other physical quantities. The logarithm of the number of the microstates is the entropy that mysteriously has a propensity to grow to its maximum.
2. Networks Thermodynamics
Communication and networks are the cornerstones of life. Whittaker [1] Nyquist [2] and Shannon [3] have shown that every kind of information can be expressed by a file comprises a sequence of “1” and “0” bits.
A file of N bits can carry 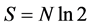 entropy, and if the bits are classical harmonic oscillators, its associated physical entropy is
entropy, and if the bits are classical harmonic oscillators, its associated physical entropy is 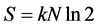 where k is the Boltzmann constant [4] .
where k is the Boltzmann constant [4] .
In a way, networks are similar to a file. If we define a link as a unidirectional connection between two nodes, then a network can be described as a sequence of N nodes having each integer number links. If the total number of links in the net is P then the number of links per node can vary from 1 to  at the maximum, as we want any node to have at least one connection to the net.
at the maximum, as we want any node to have at least one connection to the net.
From a statistical-mechanics view, a file is a sequence of N states, and the particles are the “1” bit. A network is a sequence of N states, and the particles are the “1” link. However, there is a difference; in a file it is impossible to have more than one particle in a state, but in a network the number of particles can be any integer. In physics, particles that cannot be more than one in a state are called Fermions (i.e. atoms, molecules, quarks and leptons), and particles that do not have such a restriction (Pauli exclusion principle) are called Bosons (i.e. photons, phonons and particles having spin 0, 1, 2…). The fermions and bosons have obviously different statistical properties that are well known. In fact, the name fermion was given to particles that behave according to Fermi-Dirac statistics, and the name Boson was given to particles that behave according to Bose-Einstein statistics. The origin of the differences between bosons and fermions is their different number of microstates.
In many networks in nature the number of links is much higher than the number of nodes. For example, in a social network, where a person is a node and a connection to acquaintance is a link, even a loner usually has a few links. The distribution of links in networks nodes receives a considerable attention [5] -[7] . It was found that the distribution of links in nodes has the shape of a “long tail” to the right. Namely, few nodes have many links, and the majority of links have fewer links. In statistical-mechanics language: few states have many particles and many states have few particles. It should be noted that this distribution is the classic approximation of Planck’s statistics that was suggested by him in his famous equation for the distribution of photons in radiation modes in a black body [8] . The long tail distribution is substantially different from the canonic Gaussian distribution, in which most of the states have the average number of particles [9] . Recently it was shown that the maximum entropy distribution of a network in the limit in which the number of links is much higher than the number of nodes obeys Zipf law [9] .
First we calculate the entropy  of file having P fermions in N states. Than we show that adding one bit add a constant amount of entropy namely,
of file having P fermions in N states. Than we show that adding one bit add a constant amount of entropy namely,
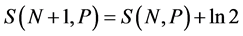 . (1)
. (1)
Later we calculate the entropy of a network having P bosons in N states. Than we show that adding one state the entropy increase is function of 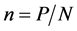 namely,
namely,
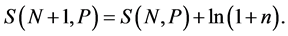 (2)
(2)
We use the Boltzmann definition of entropy for fermions [10] .
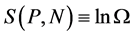 and
and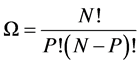 is the number of microstates. We make use of Stirling formula, namely,
is the number of microstates. We make use of Stirling formula, namely, 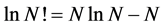 and obtain,
and obtain,
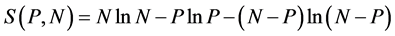
If we designate probability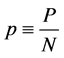 , the entropy can be written as;
, the entropy can be written as;
 (3)
(3)
It should be noted that the maximum entropy solution for Equation (1) for 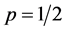 yields,
yields,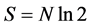 .
.
Therefore, it is clear that Equation (1) is true. One should ask about the change in p, when we add a bit. The answer is that the bit is uncertainty. Since Alice does not know its value, she assumes that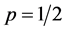 . Therefore, each bit carries
. Therefore, each bit carries 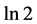 entropy, or in log base 2, one bit.
entropy, or in log base 2, one bit.
For bosons, the number of microstates is given by [11] ,
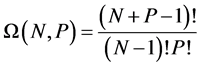 therefore, adding one node yields,
therefore, adding one node yields,

We designate occupation number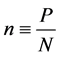 .
.
Therefore,
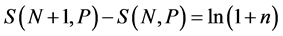 .
.
In general, networks can be described by two dimensional matrixes in which any matrix element 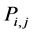 designates the number of links from a node
designates the number of links from a node  to node
to node 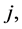 and therefore any element
and therefore any element  has an opposite direction element
has an opposite direction element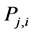 . In some networks (i.e. communication networks), the links can change their nodes and direction and therefore the number of microstates of the incoming links is identical to the number of the outgoing links, therefore
. In some networks (i.e. communication networks), the links can change their nodes and direction and therefore the number of microstates of the incoming links is identical to the number of the outgoing links, therefore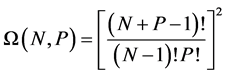 , and similarly,
, and similarly,
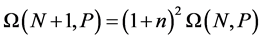
or,
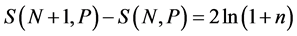 .
.
In general, the entropy increase will be between  and
and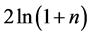 .
.
3. Conclusions
We see that unlike a binary file in which the bit carries a constant amount of uncertainty that is independent in the file in which it is transmitted, a node has an extra entropic benefit to join high occupation number nets.
High occupation number boson gas statistics can be applied for many phenomena in life. In the Internet, the sites are the states and the surfers are the particles. In the publishing market, the titles are the states and the readers are the particles. In text, the words are the states and their number is the particles, etc. In these examples one can find the long tail distributions (i.e. Planck-Benford and Zipf distributions) [12] . Our natural tendency to join the crowd may be viewed as the propensity of entropy to give a higher priority to be added to highly linked networks rather than to small ones.
Acknowledgements
I thank R. D. Levine for his criticism and H. Kafri for her help.
References
- Whittaker, E.T. (1915) On the Functions Which Are Represented by the Expansions of the Interpolation Theory. Proceedings of the Royal Society of Edinburgh, Section A, 35, 181-194.
- Nyquist, H. (1928) Certain Topics in Telegraph Transmission Theory. Transactions of AIEE, 47, 617-644.
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423, 623-656.
- Kafri, O. and Kafri, H. (2013) Entropy—God’s Dice Game. Create Space. 130-136. http://www.entropy-book.com/
- Barabási, A.L. (2002) Linked: The New Science of Networks. Perseus Books Group, New York.
- Barabási, A.L. and Réka, A. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512. http://dx.doi.org/10.1126/science.286.5439.509
- Barabási, A.L. and Oltvai, Z. (2004) Network Bioloy. Nature Reviews Genetics, 5, 101-113. http://dx.doi.org/10.1038/nrg1272
- Planck, M. (1901) Über das Gesetz der Energieverteilungim Normalspectrum. Annalen der Physik, 4, 553. http://dx.doi.org/10.1002/andp.19013090310
- Kafri, O. (2009) The Distributions in Nature and Entropy Principle. http://arxiv.org/abs/0907.4852
- Kafri O. and Kafri H. (2013) Entropy—God’s Dice Game. Creatspace, Seatle, 187.
- Kafri O. and Kafri H. (2013) Entropy—God’s Dice Game. Creatspace, Seatle, 198.
- Kafri O. and Kafri H. (2013) Entropy—God’s Dice Game. Creatspace, Seatle, 208.

