Natural Science
Vol.5 No.12(2013), Article ID:41561,5 pages DOI:10.4236/ns.2013.512156
Derivation of force constants based on the electric field gradient
![]()
1Institute of Atomic and Molecular Physics, Sichuan University, Chengdu, China; *Corresponding Author: zhuxm@scu.edu.cn
2China Academy of Engineering Physics, Mainyang, China
Copyright © 2013 Zhenghe Zhu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Zhenghe Zhu et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received 4 August 2013; revised 4 September 2013; accepted 11 September 2013
Keywords: Full Relativistic Quantum Mechanical Theory; Electric Quadrupole Moment; Electric Field
ABSTRACT
The present work devotes to studying the electric properties: electric quadrupole moment and electric field gradient (EFG) of molecules PdH and (PdH)−2 based on the full relativistic theory. It is the first time to explore that the force constants are essentially caused by electric field gradients, and indirectly with spectroscopic data. If EFG is positive, zero or negative, then the  will be positive, zero or negative. Therefore, second order force constants are adjustable to changing the intensity of EFG.
will be positive, zero or negative. Therefore, second order force constants are adjustable to changing the intensity of EFG.
1. INTRODUCTION
The force constants of diatomic molecules, in general, are derived from spectroscopic data [1], or may be determined by a least-square fitting to the data of quantum mechanic calculations [2], and the latter is time tediously consuming and complicated. If the force constants and dissociation energy are known, the calculations of diatomic potential are numerically straightforward.
It is explored that the force constants are essentially connected with the electric field gradient (EFG), and indirectly with spectroscopic data. There are some works for the calculations of the electric field gradient using non-relativistic or relativistic quantum mechanic [3-5]. The present work has evaluated the EFG of molecules PdH and (PdH)−2 based on the full relativistic quantum mechanic.
2. THE FULL RELATIVISTIC THEORY
Symmetry plays an important role for quantum mechanical theory. There are three levels for quantum mechanical method: Non-relativistic based on the single point group, relativistic based on the double group [6,7] and relativistic based on the full symmetry group or quaternion symmetry [8,9].
In consideration of the equivalence of space and time, for the relativistic theory based on the full symmetry group or quaternion symmetry, the time reversal symmetry operation is included in the symmetry group. It is well known that the product of two space symmetry operators is represented by the product of the corresponding unitary matrices in the theory of group representation, however, time reversal symmetry operation is an antiunitary operator. The inclusion both of space and time operations, the group is called the full symmetry group, and their group representation is called a co-representation, this nomenclature is introduced by Wigner [8,9]. The co-representation is not unitary representation; however, it is still possible to be broken down to irreducible form. The third level, i.e., relativistic quantum mechanical theory based on the full symmetry group or quaternion symmetry is applied by the work of T. Saue and the others.
Time reversal operator or called Kramer operator [7, 10,11] is defined as follows
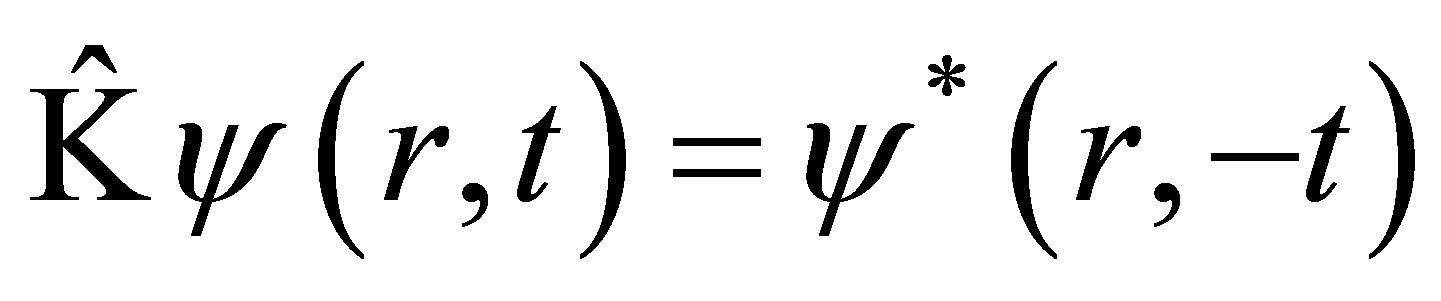 (1)
(1)
If Hamiltonian  is a real function of r, then
is a real function of r, then
 (2)
(2)
i.e.
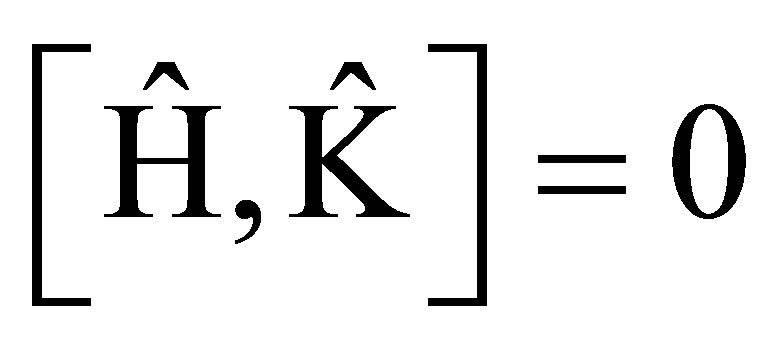 (3)
(3)
The commutator (3) is the necessary and sufficient condition for two operators  and
and  having the same set of eigenfunctions, that is ,the state is invariant to time reversal(motion reversal).
having the same set of eigenfunctions, that is ,the state is invariant to time reversal(motion reversal).
It is proved that time reversal operator is antiunitary [10,11], i.e.
 (4)
(4)
It is also anti-linear operator.
Kramer theorem [7,8,10,11]: It can be proved that  corresponding to J value of half odd integer, i.e. fermions, there will be the new double degeneracy by time reversal; and
corresponding to J value of half odd integer, i.e. fermions, there will be the new double degeneracy by time reversal; and  corresponding to J value of integer, i.e. bosons, there will be no double degeneracy, where
corresponding to J value of integer, i.e. bosons, there will be no double degeneracy, where  identity.
identity.
For the time-independent Dirac equation
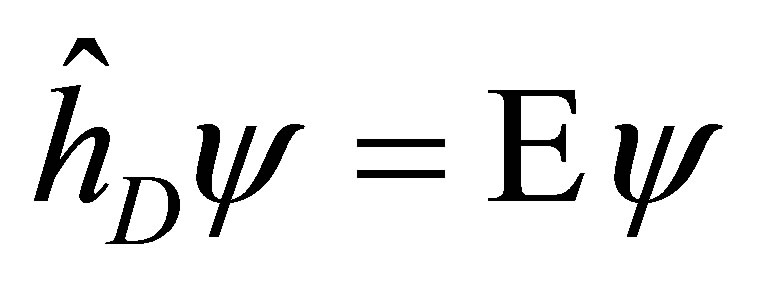 (5)
(5)
where 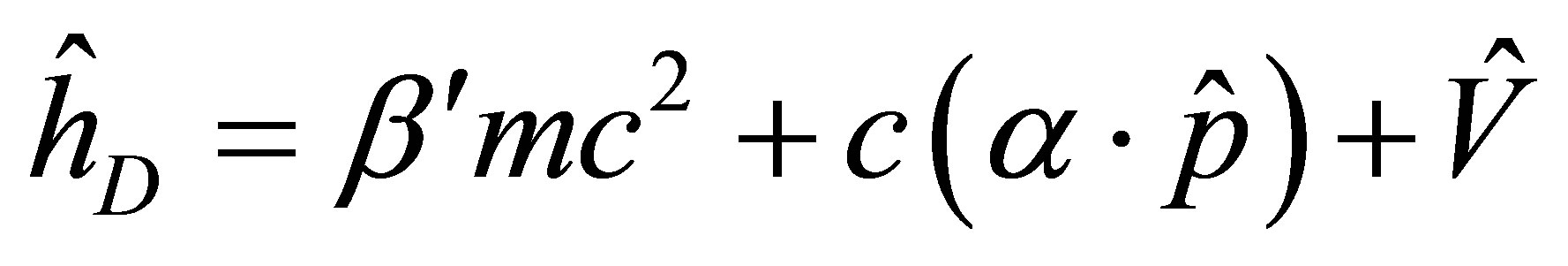
where, ;
;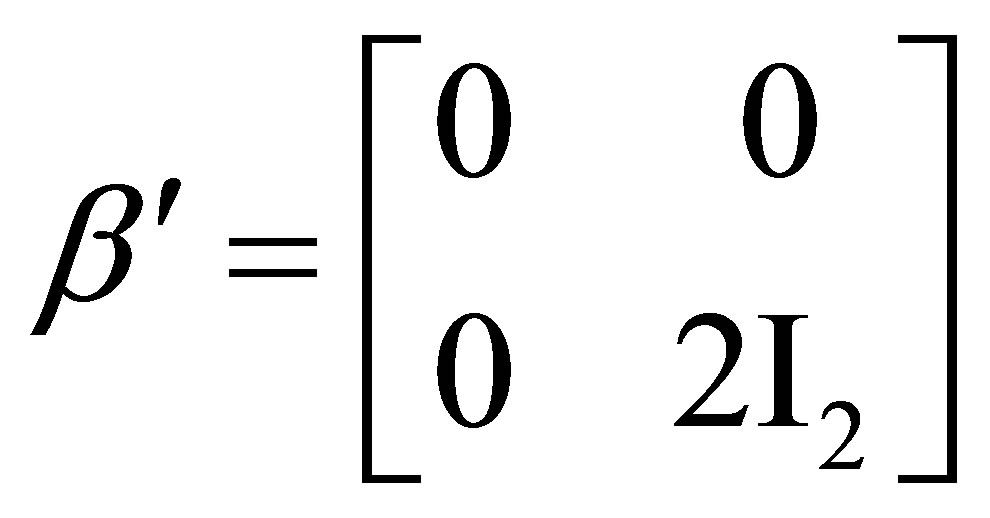 ; (6)
; (6)
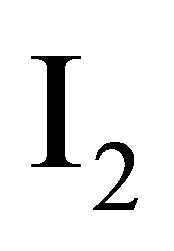 —
— Unit matrix.
Unit matrix.
And Pauli spins matrices
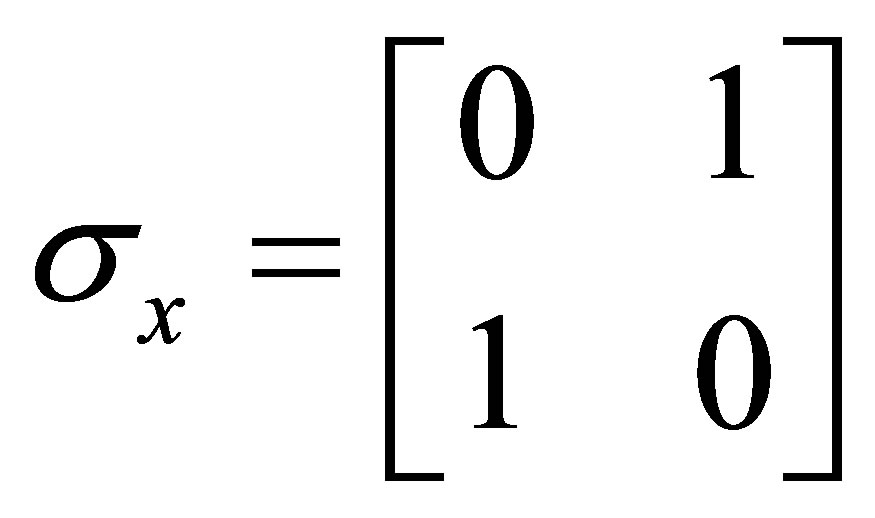 ;
;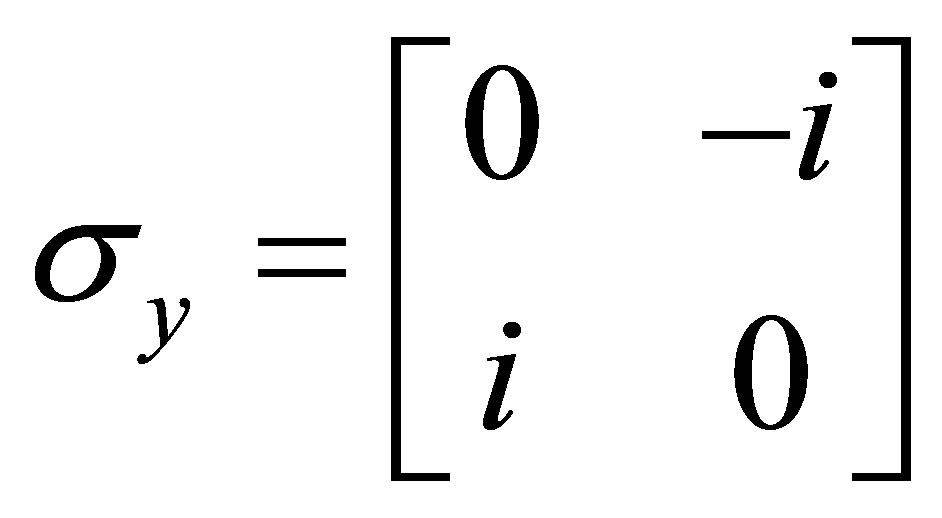 ;
;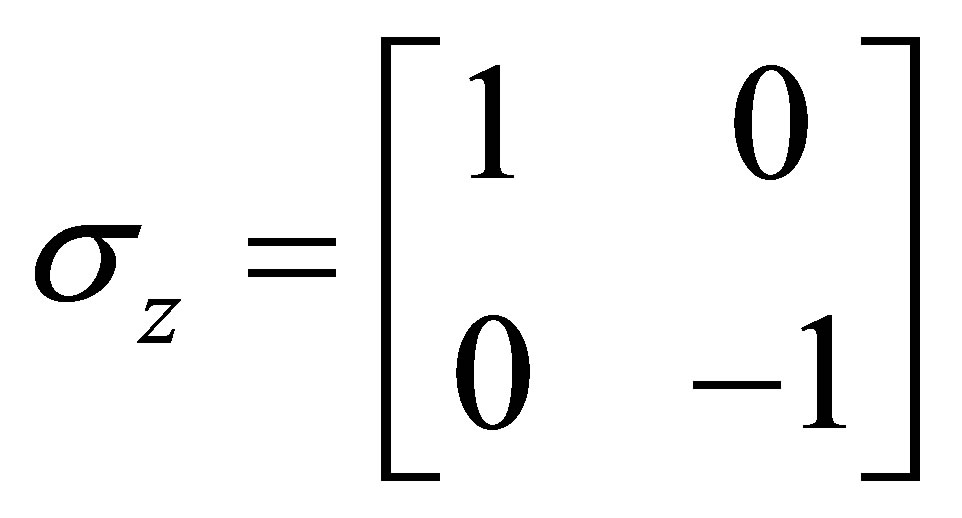 (7)
(7)
If , it is the Dirac equation of free electrons.
, it is the Dirac equation of free electrons.
Now, time reversal operator is defined using another equivalent method, i.e. Kramer theorem [8,9], in which , that is
, that is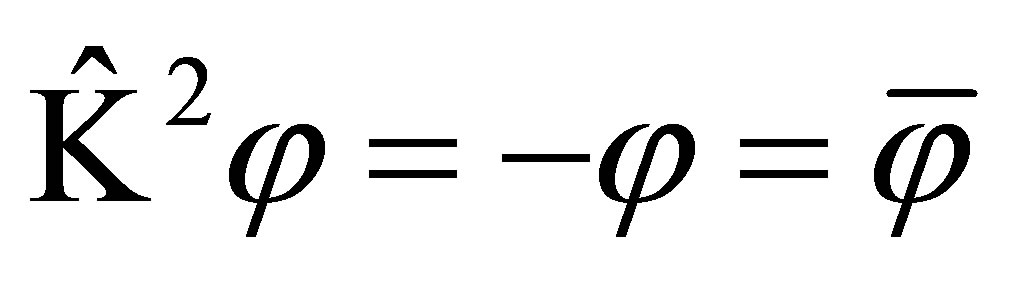 , in which the state are recovered by twice of time reversal, however, the wave function is changed to the negative; If
, in which the state are recovered by twice of time reversal, however, the wave function is changed to the negative; If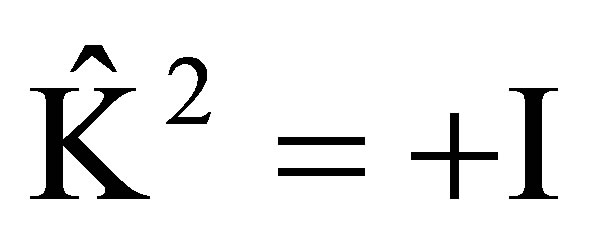 , that is
, that is , in which the state are recovered by twice of time reversal, the wave function is unchanged. Then
, in which the state are recovered by twice of time reversal, the wave function is unchanged. Then  and
and  are said to form a Kramers pair. Therefore, the operator can be expanded in terms of Kramer’s partners
are said to form a Kramers pair. Therefore, the operator can be expanded in terms of Kramer’s partners  and
and . For example, Hermitian of one-electron operator [8,9] is defined as follows
. For example, Hermitian of one-electron operator [8,9] is defined as follows
 (8)
(8)
where
 ,
,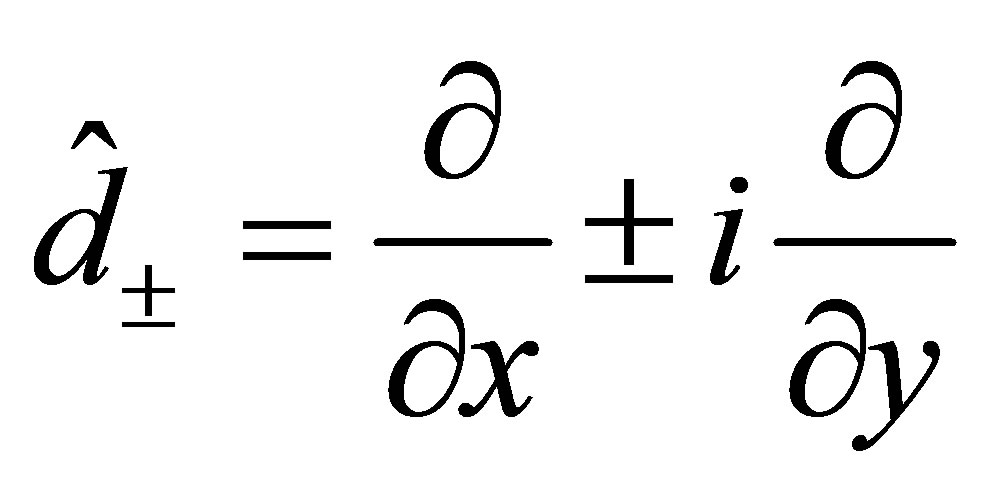 . (9)
. (9)
It is easy to know
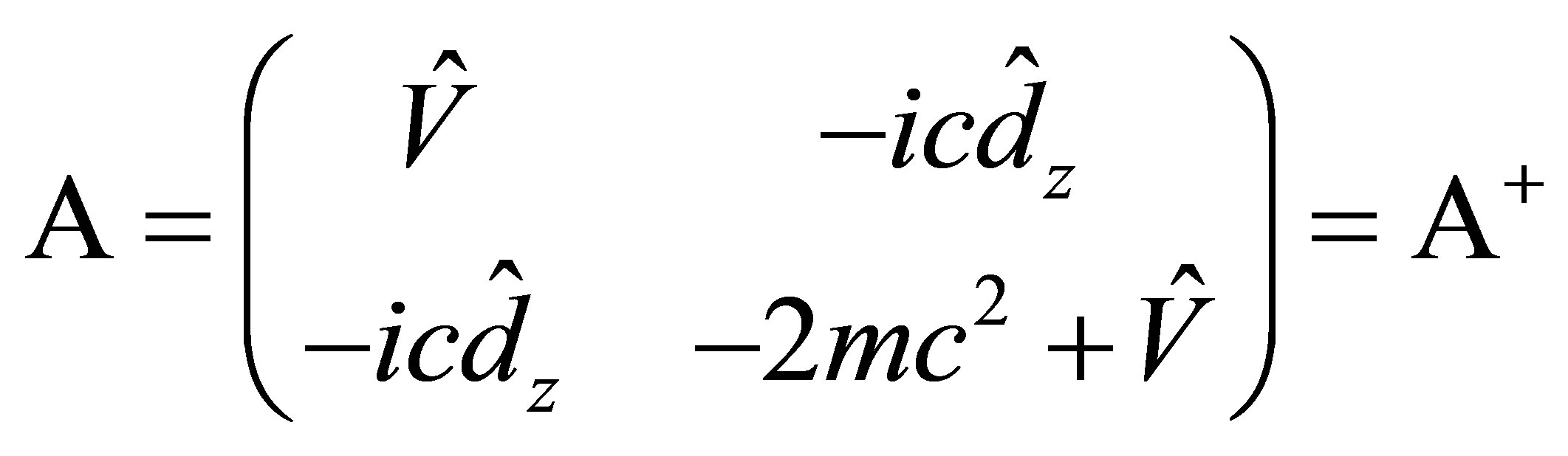 (10)
(10)
 (11)
(11)
That is, A is a Hermitian and B is antihermitian. For Kramer’s partners, Dirac operator  can be expressed as
can be expressed as
 (12)
(12)
where,  is expressed as the quaternion, which exhibits the time reversal symmetry.
is expressed as the quaternion, which exhibits the time reversal symmetry.
Quaternion algebra [12] was developed by Hamilton and Fresenius, however, limited applications of quarternion in quantum mechanics have been made in recent years.
Quaternion is expressed as
 (13)
(13)
where
 (14)
(14)
where ,
, 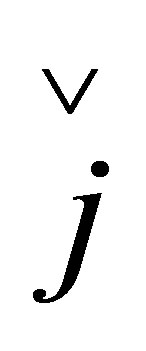 ,
, 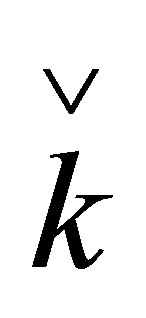 are quaternion units, i-imaginary,
are quaternion units, i-imaginary,  ,
,  ,
,  and
and 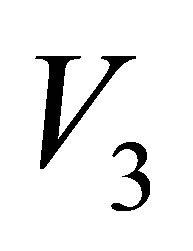 are real part,
are real part, 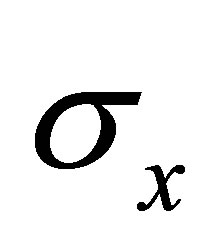 ,
, 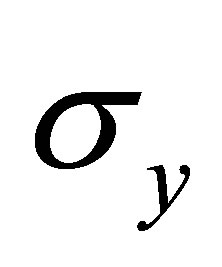 and
and  are Pauli spins matrices in (7). Quaternion includes 3-dimension complex space and one dimension real space. It is known from (7) to (11) that quaternion algebra includes both time and space reversal symmetry, then, it is called the full symmetry group, its matrix representation is called co-representation. The
are Pauli spins matrices in (7). Quaternion includes 3-dimension complex space and one dimension real space. It is known from (7) to (11) that quaternion algebra includes both time and space reversal symmetry, then, it is called the full symmetry group, its matrix representation is called co-representation. The  in (12) is the Dirac operator of full symmetry group. The Dirac equation can therefore be rewritten into quaternion algebra form
in (12) is the Dirac operator of full symmetry group. The Dirac equation can therefore be rewritten into quaternion algebra form
 (15)
(15)
3. THE CALCULATIONS OF ELECTRIC PROPERTIES
The calculations of energy and electric properties: electric quadrupole moment, electric field gradients of molecules PdH based on the full relativistic quantum mechanical theory with the basis dyall.v2z using of program DIRAC10. The results are shown as Tables 1 and 2.
The charge distributions of dipole for molecule PdH is calculated as follows


Table 1. The energy, electric dipole and quadrupole moment of molecule PdH.
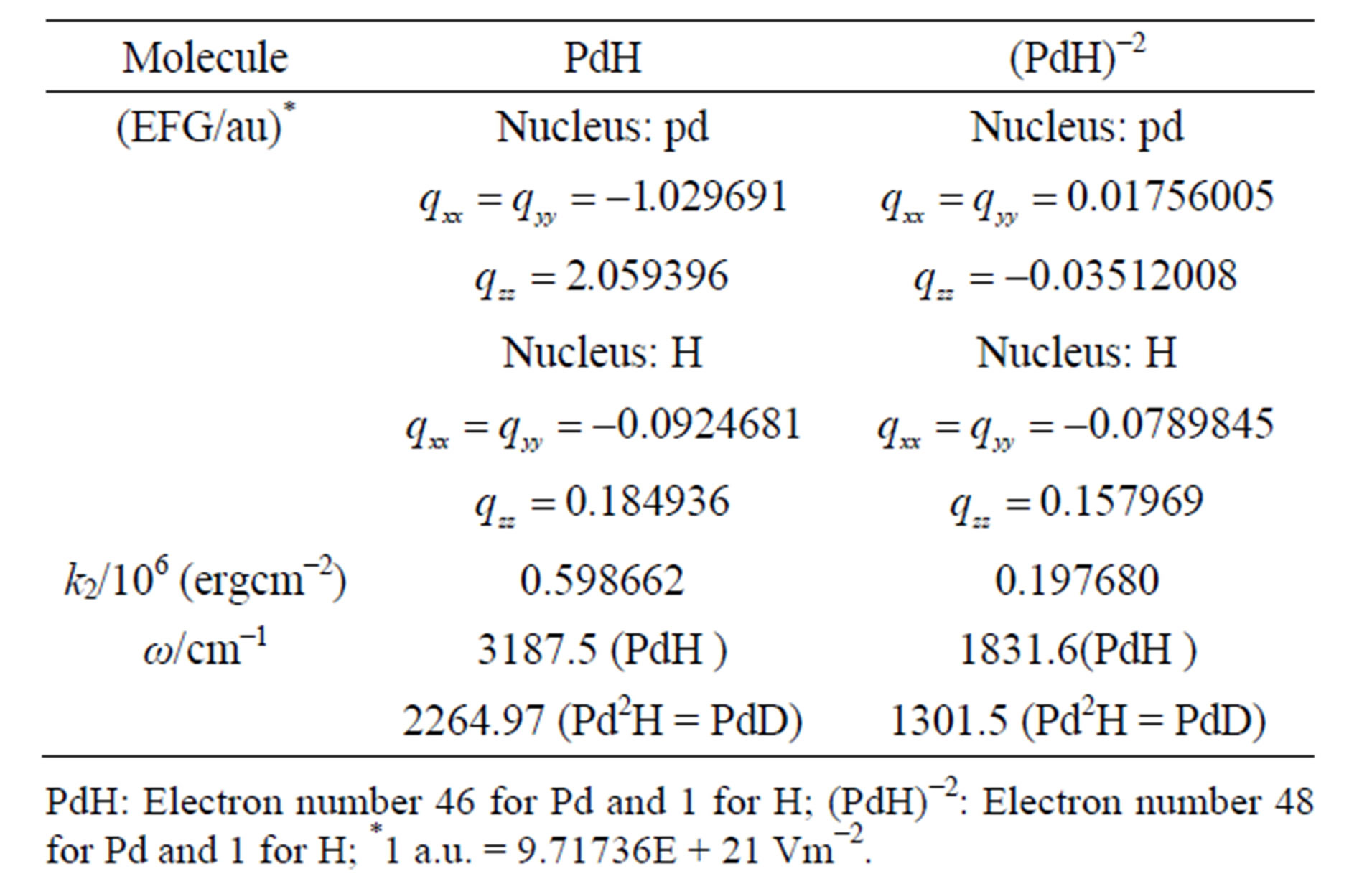
Table 2. The electric field gradients (EFG), k2 and w for molecules.
However, its quadrupole is the second-rank tensor with two dimension charge distribution (vertical plane ), Figure 1 in which the unit of charge distributions is 10-19 C, C-coulombThe
), Figure 1 in which the unit of charge distributions is 10-19 C, C-coulombThe 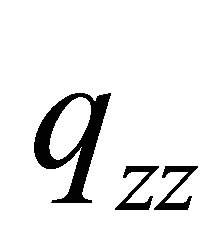 and
and 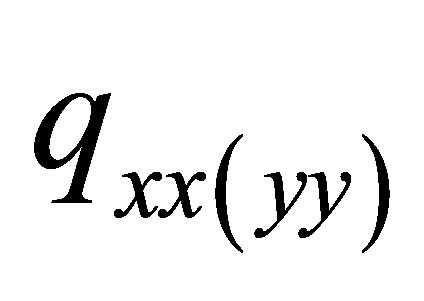 of PdH can be calculated as
of PdH can be calculated as

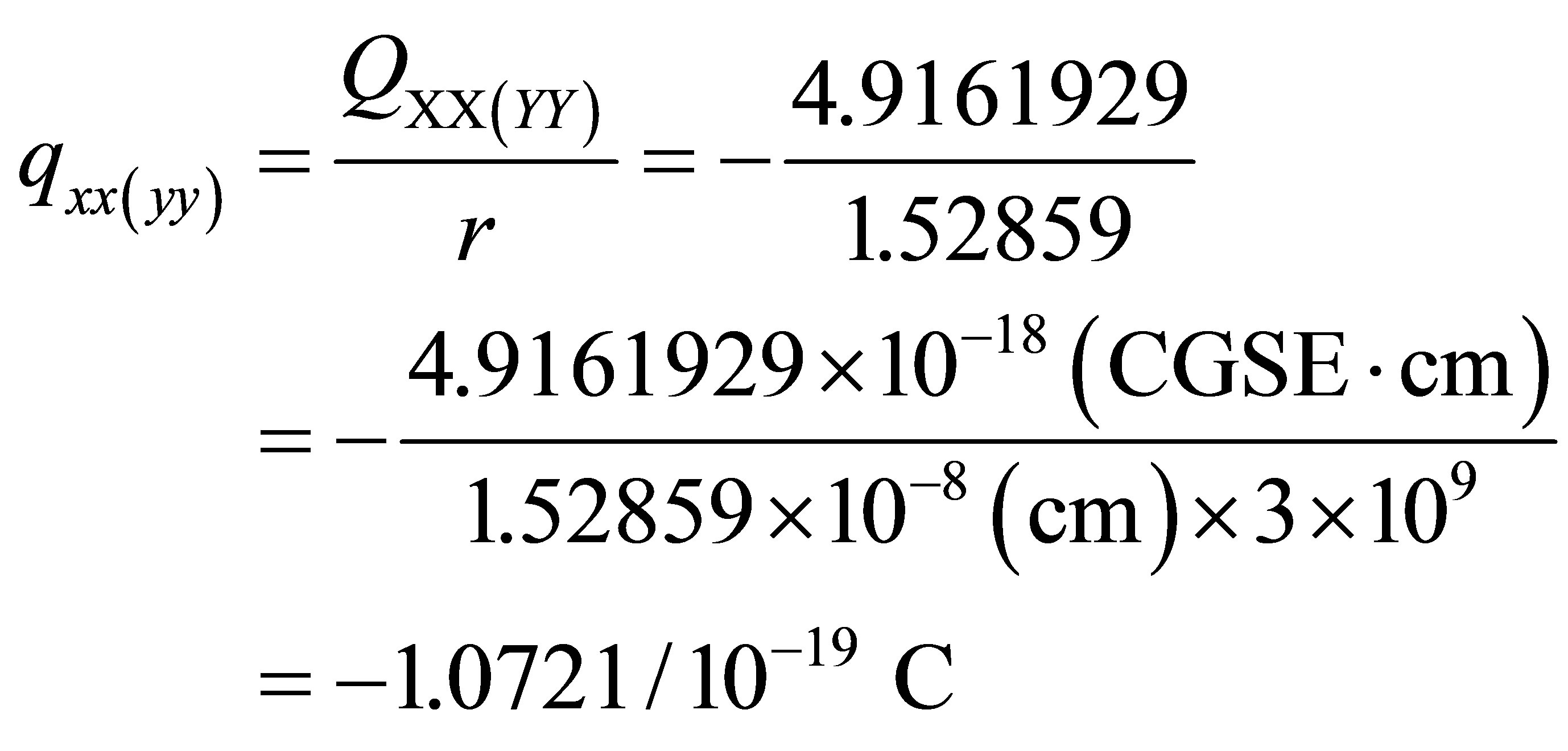
Suppose the potential of diatomic can be expressed as
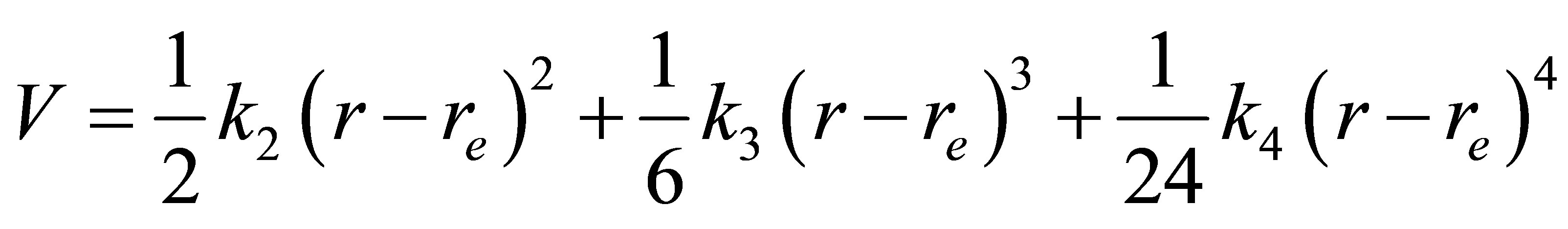 (16)
(16)
Where r is the nuclear distance and 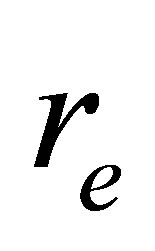 is its equilibrium nuclear distance, and
is its equilibrium nuclear distance, and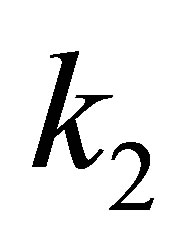 ,
, 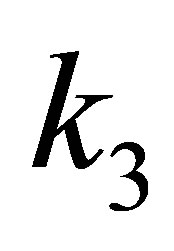 and
and  are the quadratic, cubic and quartic force constants, respectively. The negative derivative of potential with respect to bond distance r is the electric field force of nuclei, therefore
are the quadratic, cubic and quartic force constants, respectively. The negative derivative of potential with respect to bond distance r is the electric field force of nuclei, therefore
 (17)
(17)
where E is the electric field strength, q is the electric charge.
From (17), it leads to the electric field gradient 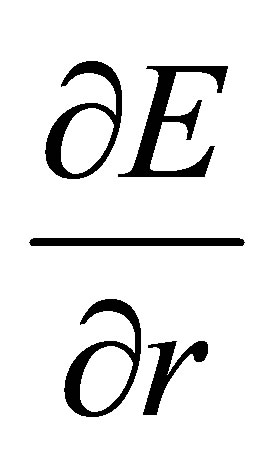 (EFG)
(EFG)
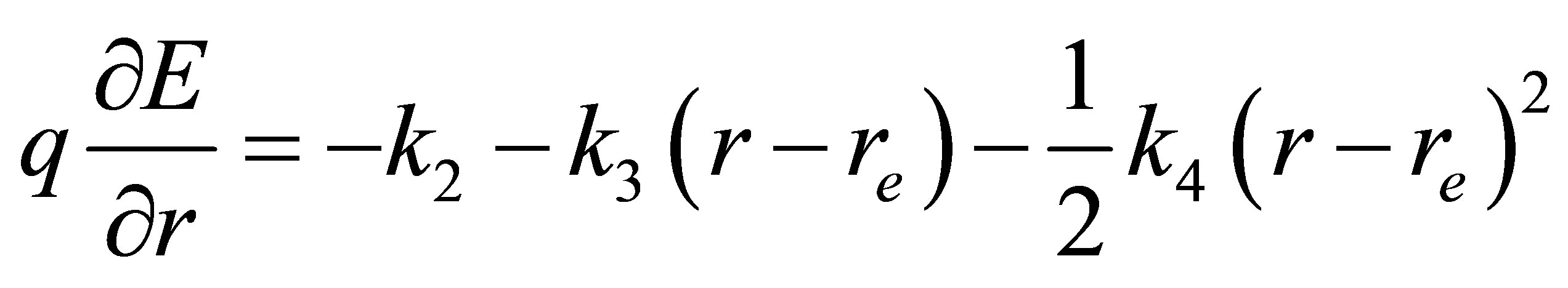 (18)
(18)
If r = re, then, the quadratic force constant  will be
will be
 (19)
(19)
where q is negative and take its absolute value. If EFG is positive, zero or negative, then, the 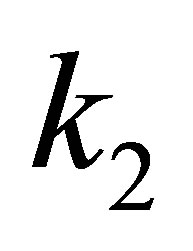 will be positive, zero or negative. If we want the
will be positive, zero or negative. If we want the 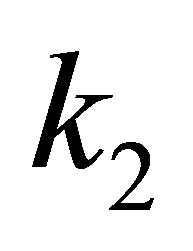 to be zero or negative, it is possible to make the EFG descended or tend to negative.
to be zero or negative, it is possible to make the EFG descended or tend to negative.
Suppose there is 1 au of electric charge and at 1au of electric field gradient, the quadratic force constant 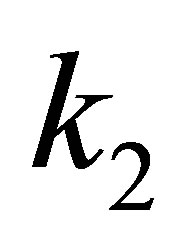
 (20)
(20)
For neutral molecule PdH, i.e., electron number of 47, and the 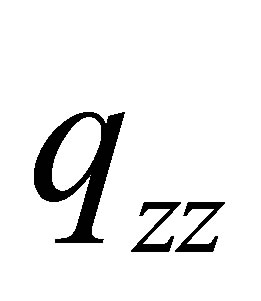 = 2.059396 for Pd and
= 2.059396 for Pd and 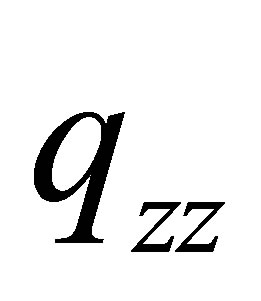 = 0.184936 for H, and their Mulliken Atomic Charges: Pd = 0.037613, H = −0.037613. Then
= 0.184936 for H, and their Mulliken Atomic Charges: Pd = 0.037613, H = −0.037613. Then
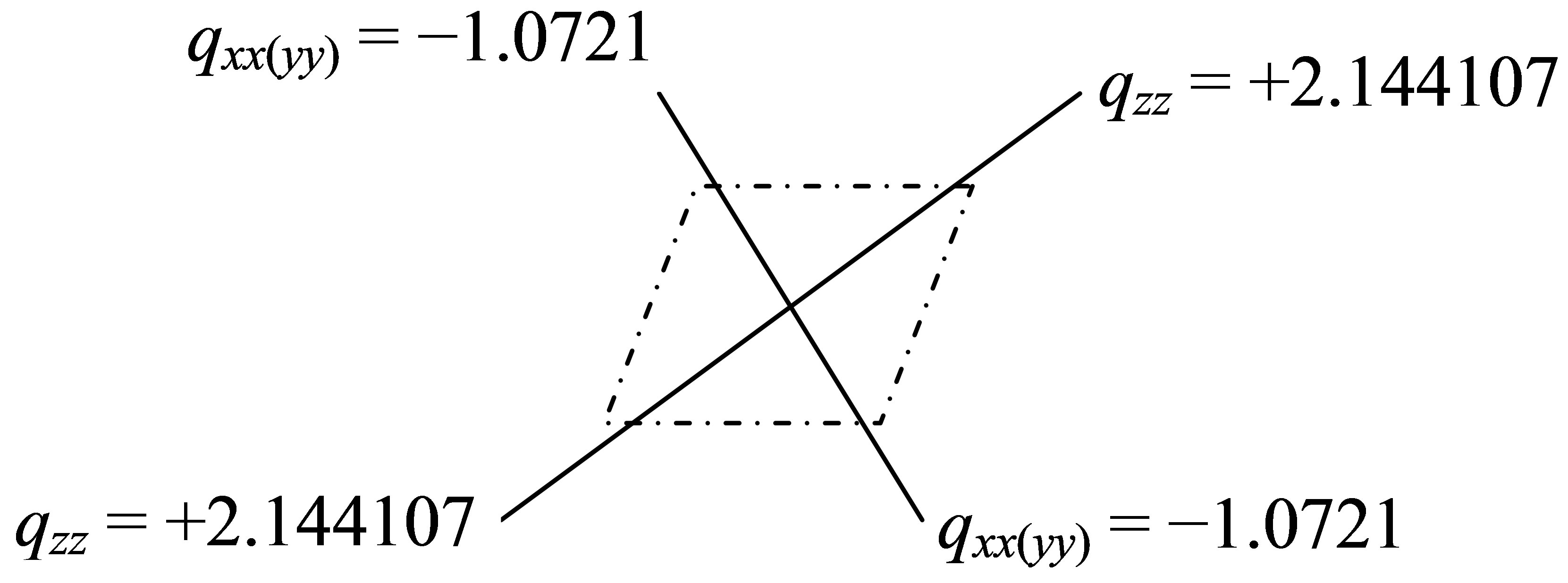
Figure 1. The quadrupole charge distribution of PdH.
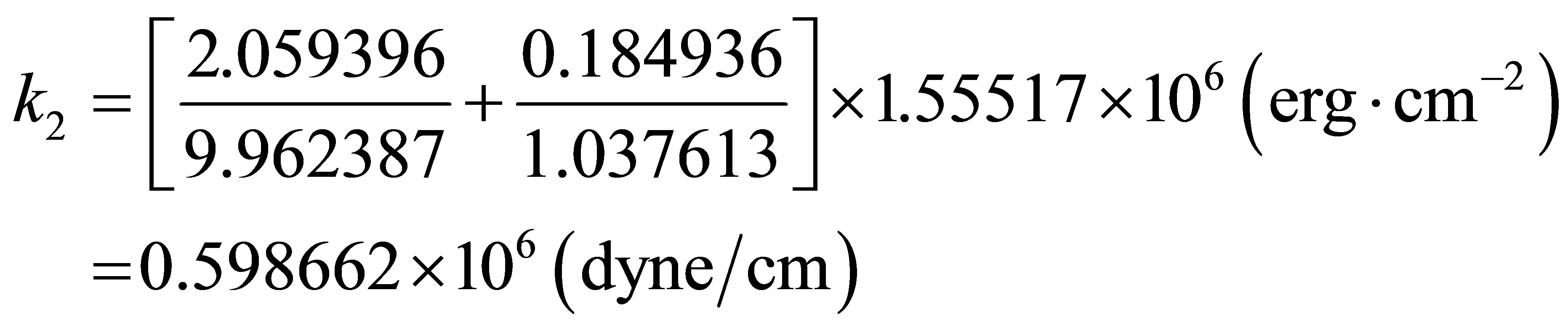
And Harmonic frequencies

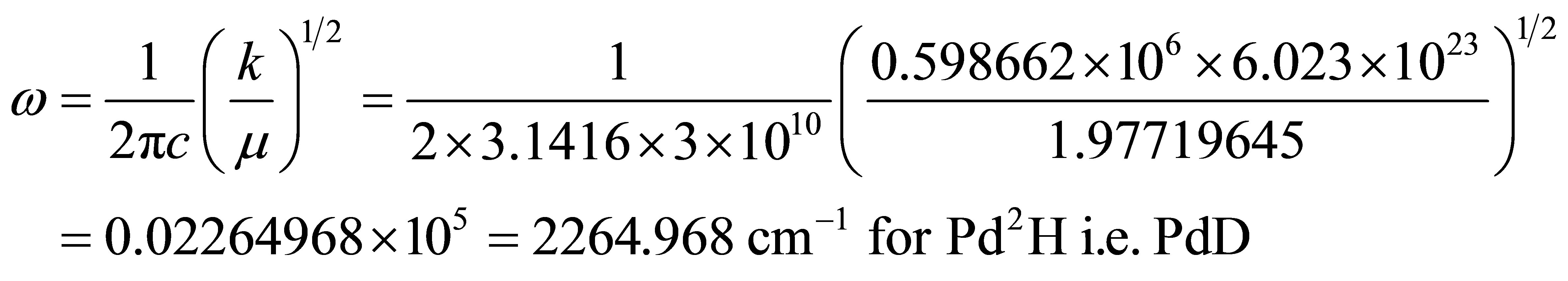
where 1.97719645 is the reduced mass of PdD.
For (PdH)-2, i.e., Electron number of 49, i.e., and the  for Pd and
for Pd and 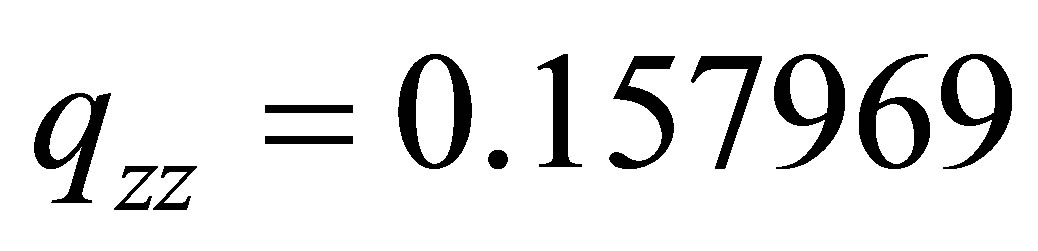 for H, and their Mulliken Atomic Charges: Pd = -1.785709 , H = -0.214291. Then
for H, and their Mulliken Atomic Charges: Pd = -1.785709 , H = -0.214291. Then

And Harmonic frequencies
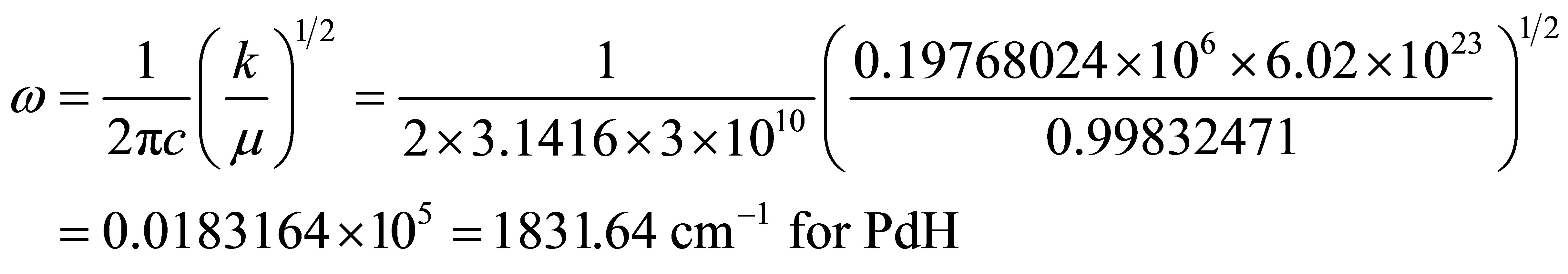
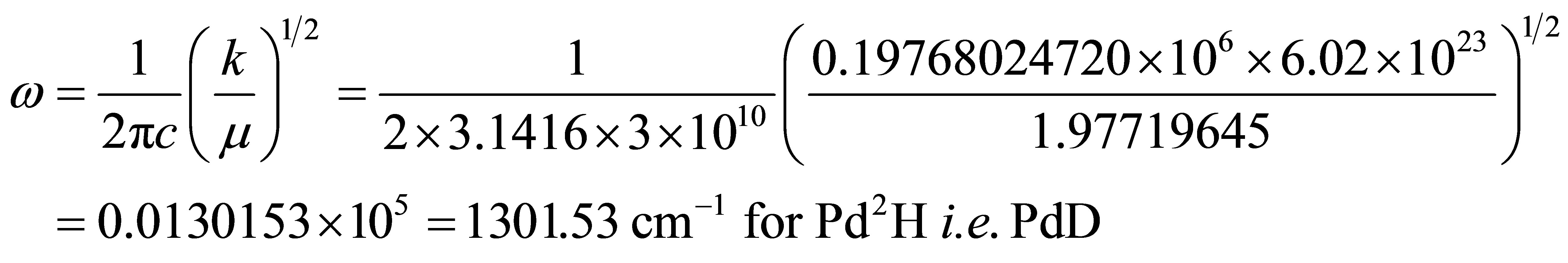
where 1.97719645 is the reduced mass of PdD.
All the electric field gradients (EFG), quadratic force constants  and Harmonic frequencies
and Harmonic frequencies  for molecules are listed in Table 2.
for molecules are listed in Table 2.
4. CONLUSIONS
From Equation (19), it is proved that the second order force constant is directly derived from electric field gradients EFG. Therefore, it is the first time to explore that the force constant is essentially caused by electric field gradients, and the second order force constant and its harmonic oscillator frequency have been derived from electric field gradients. However, the force constants are usually derived from spectroscopic data; however, it is indirect with spectroscopic data. Therefore, this is the supplemental to the spectral values.
Momentously, the second order force constants are adjustable to changing the intensity of EFG. If EFG is positive, zero or negative, then, the  will be positive, zero or negative. It is obvious to see from Table 2 that
will be positive, zero or negative. It is obvious to see from Table 2 that 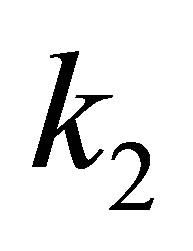 is descended from 0.59866×106 erg·cm-2 of PdH down to 0.19768×106 erg·cm-2 of (PdH)-2, where, it’s EFG from
is descended from 0.59866×106 erg·cm-2 of PdH down to 0.19768×106 erg·cm-2 of (PdH)-2, where, it’s EFG from  that is down to
that is down to .
.
The linear charge distributions, ±0.73647/10-19 C, of dipole moment for molecule PdH is much less than its two-dimension charge distribution of quadrupole moment qzz = 2.144107/10-19 C and qxx(yy) = -1.0721/10-19 C. The charge distribution of PdH could be comparable with that of molecules HBr or HCl; however, it does not like HF, to see Table 3 of references [13], and therefore quadrupole
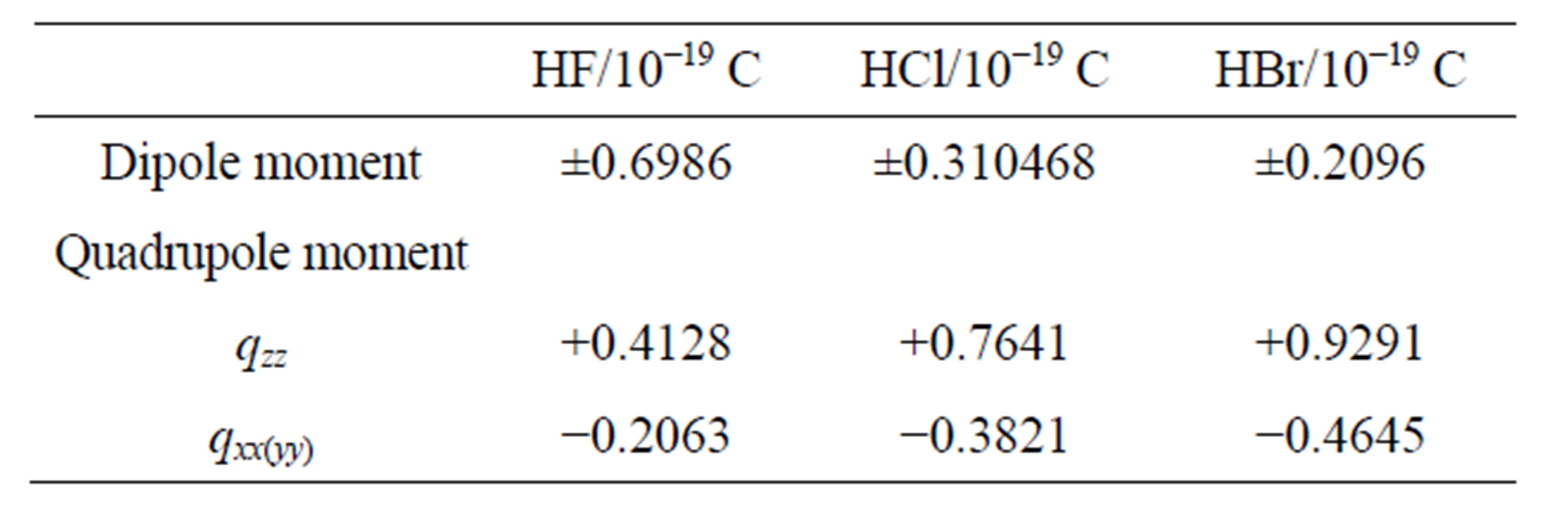
Table 3. The linear charge distributions of molecule (HX, X = F, Cl, Br) [13].
charge distributions are quite characteristic for electric properties.
REFERENCES
- Huber, K.P. and Herzberg, G. (1979) Molecular spectra and molecular structure I-IV, Van Nostrand Reinhold Company.
- Murrell, J.N. (1984) Molecular potential energy functions. John Wiley, New York.
- Neese, F., Wolf, A., Fleig, T., Reiher, M. and Hess, B.A. (2005) Calculation of electric-field gradients based on higher-order generalized Douglas-Kroll-Hess transformations. Journal of Chemical Physics, 122, 204107-204117. http://dx.doi.org/10.1063/1.1904589
- Visscher, L., Enevoldsen, T., Saue, T. and Oddershede, J. (1998) Molecular relativistic calculations of the electric field gradients at the nuclei in the hydrogen halides. Journal of Chemical Physics, 109, 9677-9684. http://dx.doi.org/10.1063/1.477637
- Mastalerz, R., Barone, G., Lindh, R. and Reiher, M. (2007) Analytic high-order Douglas-Kroll-Hess electric field gradients. Journal of Chemical Physics, 127, 074105-047117. http://dx.doi.org/10.1063/1.2761880
- Luding, W. and Falter, C. (1996) Symmetries in physics. Springer-Verlag Heidelberg, Berlin.
- Tinkham, M. (1964) Group theory and quantum mechanics. McGraw-Hill, New York.
- Saue, T. and Jensen, H.J.A. (1999) Quaternion symmetry in relativistic molecular calculations. Journal of Chemical Physics, 111, 6211-6222. http://dx.doi.org/10.1063/1.479958
- Saue, T. and Jensen, H.J.A. (2003) Linear response at the 4-components relativistic level. Journal of Chemical Physics, 118, 522-536.
- Zhu, Z.H. (1996, 2007) Atomic and molecular reaction statics. Science Press, Beijing.
- Zhu, Z.H. (2007) The atomic and molecular reaction statics. Science in China Series G: Physics Mechanics and Astronomy, 50, 581-590. http://dx.doi.org/10.1007/s11433-007-0054-6
- Charlie, H. (1976) Introduction to mathematical physics. Prentice Hall, Inc., Engleewood Cliffs.
- Zhu, Z.H., Meng, D.Q., Tang, Y.J. and Wan, M.J. (2012) Electric properties of molecules (HX, X = F, Cl, Br) based on the full relativistic theory. Science in China Series G: Physics Mechanics and Astronomy, 42, 392-399.

