Natural Science
Vol.5 No.6(2013), Article ID:32982,5 pages DOI:10.4236/ns.2013.56089
About one form of writing of the Hardy-Weinberg law
![]()
Samara State Medical University, Samara, Russia; volobuev47@yandex.ru
Copyright © 2013 Andrey N. Volobuev et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 4 April 2013; revised 6 May 2013; accepted 14 May 2013
Keywords: Stochastic Mutagen Factor; Newgrowths; Allele; Alternation of Generations
ABSTRACT
On the basis of the Hardy-Weinberg law written down for a continuous scale of alternation of generations, populating dynamics of genome is considered at absence of mutagen influence and at presence of the mutagen factor of stochastic character. Influence of the stochastic mutagen factor as cancerogenes on the population is shown. In the countries with the homogeneous population and advanced medicine, it inevitably results in growth of death rate of the population from newgrowths to proportional a root square from time of a life of the population. The carried out research allows estimate a level of the population condition in the country from the point of view of health.
1. INTRODUCTION
The Hardy-Weinberg law was formulated in 1908 independently from each other English mathematician H. Hardy (1877-1947) and German doctor W. Weinberg (1862-1937) which was interested in genetic problems of twins. This law expresses display of Mendel laws for inheritance in a population.
The Hardy-Weinberg law in the elementary kind of two alleles of a gene establishes, that relative frequencies of genotypes in generations at autosoming inheritance correspond to term of binomial expansion  under condition of
under condition of , where p and q is the frequencies of alleles in a population [1]. For genome linked to a sex the frequencies of genotypes correspond to product
, where p and q is the frequencies of alleles in a population [1]. For genome linked to a sex the frequencies of genotypes correspond to product , where
, where  is the frequency of dominant allele A at men and
is the frequency of dominant allele A at men and  is the frequency of dominant allele at women. For recessive allele a it is accordingly
is the frequency of dominant allele at women. For recessive allele a it is accordingly  and
and .
.
Though the Hardy-Weinberg law has populating character, but the good description of a population with the help of this law is inconvenient. The matter is that the population will consist of family trees which crossed among themselves. Development of a population is a development of family trees under condition of their periodic contact.
The Hardy-Weinberg law concerns to a separate family tree. Implicitly this law includes time since alternation of generations occurs through certain time—time of a life of generation. Usually use some average time of a life of one generation 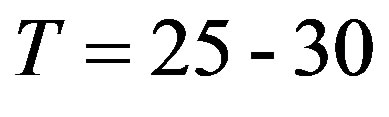 years. Thus, the Hardy-Weinberg law on time has the expressed discrete character. The population lives in continuous real time. Alternation of generations of a plenty of family trees results to that generations in a population vary actually according to a continuous time scale.
years. Thus, the Hardy-Weinberg law on time has the expressed discrete character. The population lives in continuous real time. Alternation of generations of a plenty of family trees results to that generations in a population vary actually according to a continuous time scale.
Therefore, it is interest of the writing of the HardyWeinberg law for a population existing in a continuous time scale. In this case, it will be possible to estimate the vital life of all population more correctly.
2. POPULATING DYNAMICS OF GENOME AT DISCRETE ALTERNATION OF GENERATIONS
According to the Hardy-Weinberg law the genotypes AA, Aa and aa at autosoming inheritance have the following frequency ratio:
 , (1)
, (1)
The Hardy-Weinberg balance is indifferent [2]. For autosoming inheritance it is obvious. Really, using distribution of genotypes (1) it is possible to receive, for example, the frequency of recessive allele a in the following 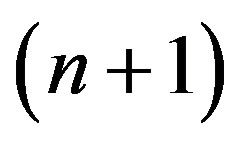 generation. For this purpose it is necessary the summation of the half frequency of heterozygote Aa and frequency of the homozygote aa:
generation. For this purpose it is necessary the summation of the half frequency of heterozygote Aa and frequency of the homozygote aa:
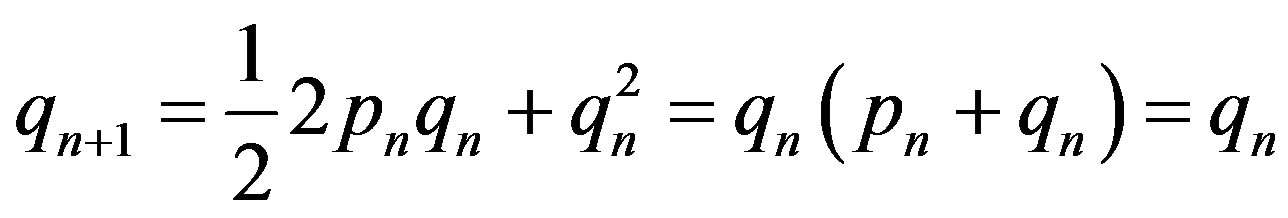 . (2)
. (2)
In the following generation the same frequency of allele a as in previous is received.
Mechanical analogy of three possible types of balance: stable—1, unstable—2, indifferent—3 it is shown on Figure 1.
Indifferent character of the Hardy-Weinberg balance results to occurrence of the external influence leading to deterioration of a population compensated of the population cannot be even if this influence has stopped. Reduction of an initial ratio of alleles is possible only due to their receipt from the outside.
For genome, linked to a sex the complex analysis is required more. At crossing in the first generation there is a following ratio of genotypes at women:
 . (3)
. (3)
Using distribution of genotypes (3), we shall find frequency of allele a at women in the following  generation:
generation:
 (4)
(4)
At the deduction (4) the following obvious formulas  and
and  are used. Formula (4) can be copied in the following kind:
are used. Formula (4) can be copied in the following kind:
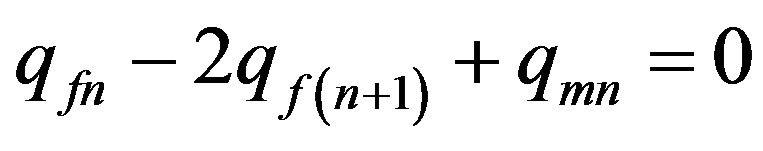 . (5)
. (5)
For convenience of the further analysis Formula (5), we shall write down with displacement on one generation back:
 . (6)
. (6)
The frequency of allele a at men is equal to the frequency of this allele at women of the previous generation . Using the given condition from (6) we shall find:
. Using the given condition from (6) we shall find:
 . (7)
. (7)
The solution of the differencing Eq.7 we search as , where in this case a is constant. Substituting this solution in Formula (7), we have:
, where in this case a is constant. Substituting this solution in Formula (7), we have:
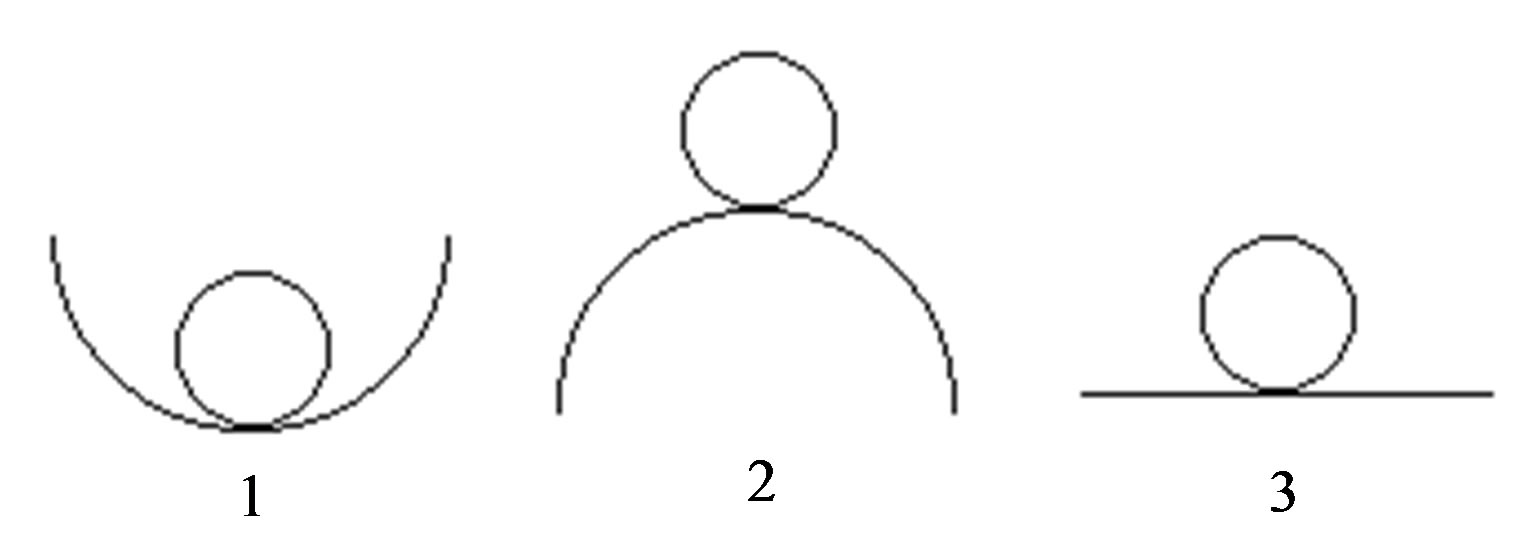
Figure 1. Mechanical realization of three possible types of balance: stable—1, unstable—2, indifferent—3.
 . (8)
. (8)
Let’s divide the Eq.8 on :
:
 . (9)
. (9)
We find two roots of the characteristic quadratic (9):
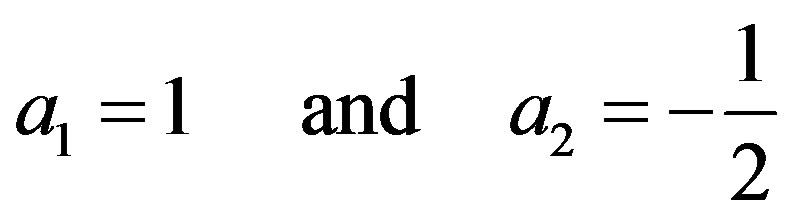 . (10)
. (10)
Hence, the general solution of the differencing Eq.7 looks like:
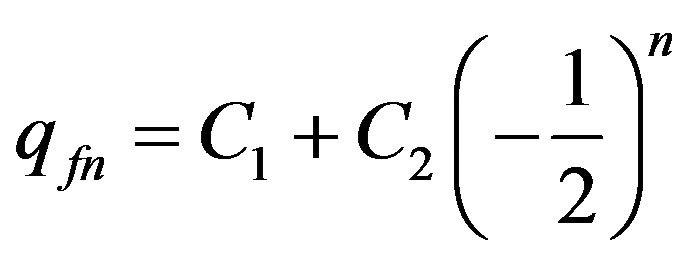 . (11)
. (11)
Constants of integration 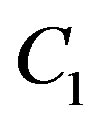 also
also 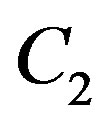 we shall find on the basis of the initial conditions: at
we shall find on the basis of the initial conditions: at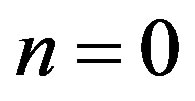 ,
, 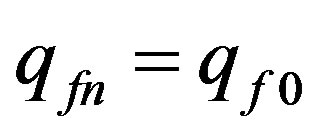 and at
and at 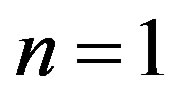 according to (4)
according to (4)
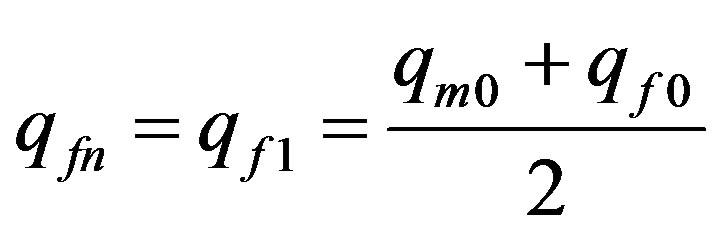 . Thus:
. Thus:
 . (12)
. (12)
Therefore the solution (11) finally looks like:
 . (13)
. (13)
3. POPULATING DYNAMICS OF GENOME AT CONTINUOUS ALTERNATION OF GENERATIONS
Let’s transit to a continuous time scale n. Under size n in this case we mean time of a life of the population, normalized on average in a population time of a life of one generation, i.e. actually dimensionless time.
Let’s find out, whether there is the differential equation having the characteristic equation similar (8). For this purpose we shall consider the differential equation:
 , (14)
, (14)
where 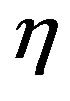 is a constant.
is a constant.
Let’s transform the Eq.14 to finite-difference form:
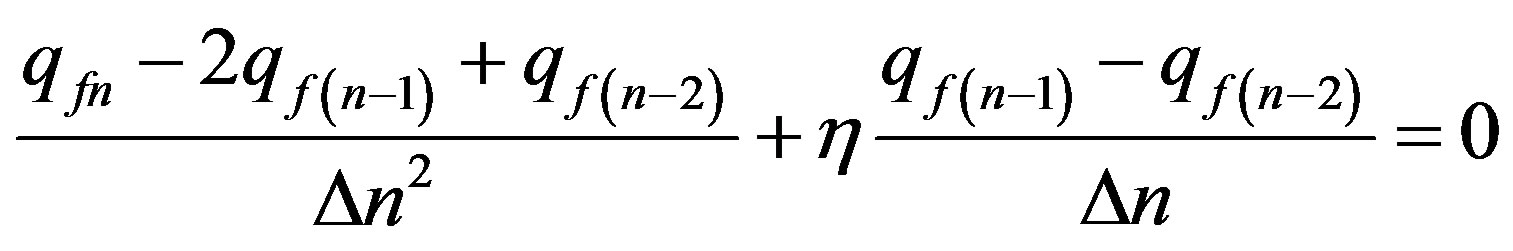 . (15)
. (15)
Uniting similar members and multiplying the Eq.15 on 2, we shall find:
 . (16)
. (16)
Let’s try of unification the Eqs.7 and 16. For this purpose it is necessary to accept:
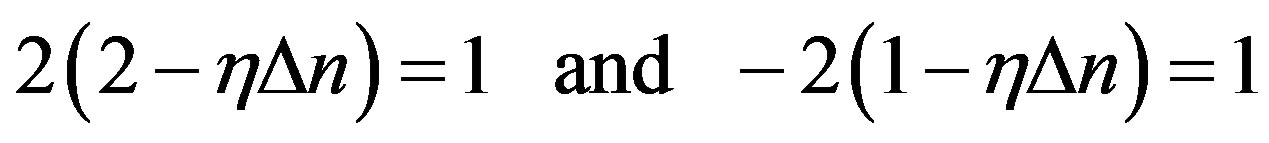 . (17)
. (17)
Wonderful feature of the Eq.17 is that they have one and too the solution:
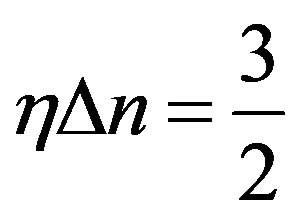 . (18)
. (18)
It means, that the difference’s Eq.7 and the differential Eq.14 can have the same characteristic equation. Taking into account (18), the Eq.14 can be copied as:
 . (19)
. (19)
The Eq.19 can be integrated once:
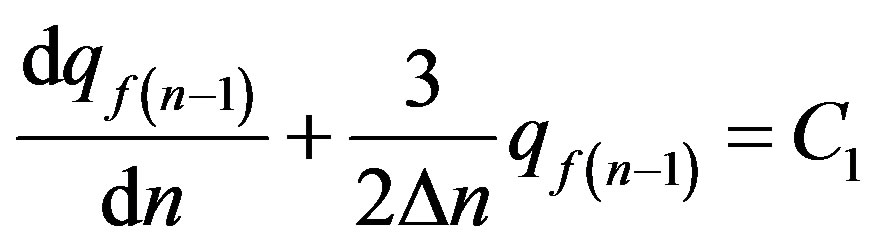 . (20)
. (20)
where  is a constant of integration.
is a constant of integration.
Further integrating the Eq.20 method of separation of variables:
 . (21)
. (21)
We shall find:
 . (22)
. (22)
Identifying the solution (22) with the solution (13), we shall find:
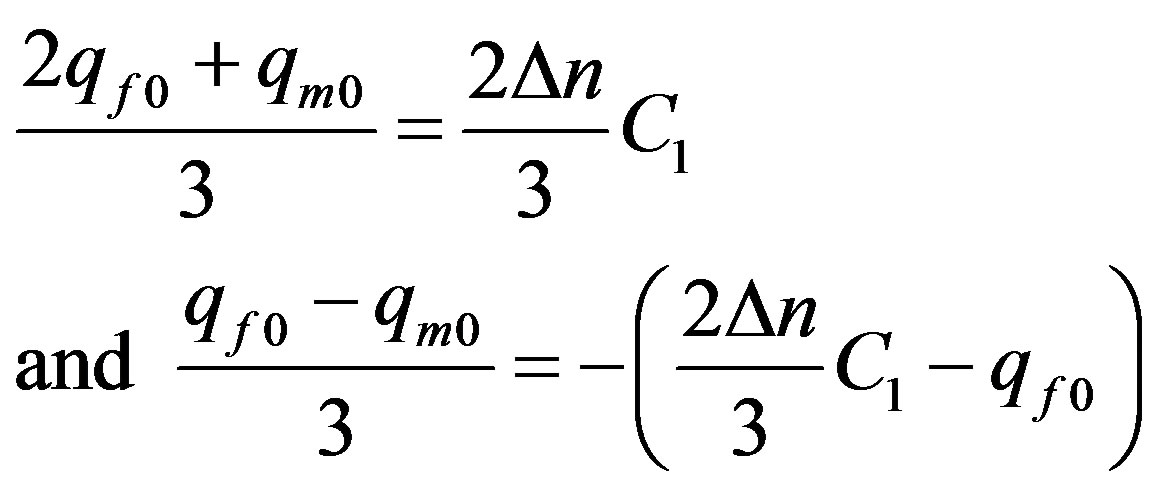 . (23)
. (23)
As one would expect, Formula (23) do not contradict each other. Hence, the solution (22) can be written down as:
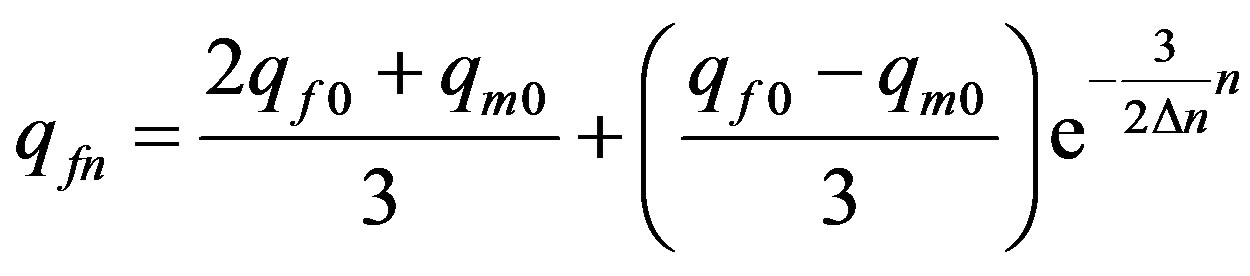 . (24)
. (24)
Formula (24) is correct for frequency of allele only in even generations. This consequence of transition to a continuous scale of generations n.
Comparing (13) and (24), for even generations, we have 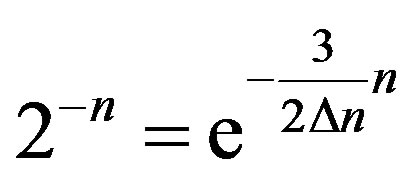 or
or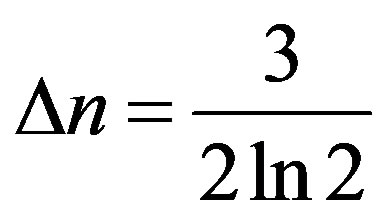 . Hence, (24) it will be transformed to a kind:
. Hence, (24) it will be transformed to a kind:
 , (25)
, (25)
that is identical to Formula (13) at even generations.
Taking into account (18) and , we find
, we find
 . Thus, the differential Eq.19 will be written down as:
. Thus, the differential Eq.19 will be written down as:
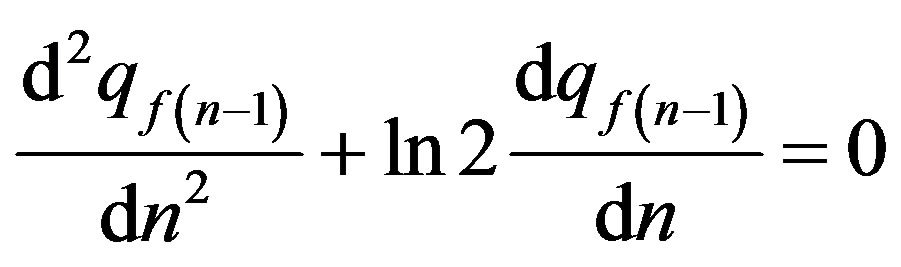 . (26)
. (26)
Formula (26) it is Hardy-Weinberg law in case of continuous alternation of generations, i.e. for a continuous time scale.
Let’s note the important feature of the found form of the Hardy-Weinberg law. In this law completely there are no reasons of alternation of generations, the reason of the termination of ability to live of the previous generation at occurrence of new generation. It results to that the population numerically indefinitely increases that contradicts the basic biological laws. Thus, there should be a way of correction of the Hardy-Weinberg law with the purpose of more correct description it of the population existence.
4. ACTION OF THE STOCHASTIC MUTAGEN FACTOR
Let’s consider existence of a population which the stochastic mutagen factor influences.
Eq.26 is the equation of indifferent balance of genome, linked with a sex, at continuous alternation of generations.
That of it to be convinced, we will address to other, well investigated physical phenomenon—the Brownian motion [3]. Brownian motion of a particle in a liquid at first sight should not exist. Really, on Brownian particle, for example, flower pollen, impacts of molecules of a liquid which are counterbalanced operate from different directions. Therefore, the most probable state of a particle is motionless. The particle should shiver only, but should not have some constant displacement from a point of supervision. Einstein and Smoluchowski have shown that physically the Brownian motion is consequence of statistical properties of the second law of thermodynamics. If the researcher has relatively a small number of molecules the essential deviation from the most probable state of system should be observed, in this case a motionless state of the Brownian particles.
Let’s note the main generality of two phenomena: the Brownian motion and existence of a population in conditions of action of the stochastic mutagen factor.
At the Brownian motion on the determined system—a particle in a liquid—stochastic force acts from the molecules of a liquid.
In a researched case on the determined system—reproductive genome—some stochastic mutagen factor acts.
At the Brownian motion the equation of movement of a particle looks like:
 , (27)
, (27)
where m is a mass of a particle, S—displacement of a particle from initial position, r—factor of resistance of medium to movement of a particle, t—time, F—the stochastic force acting on a particle from the molecules of a liquid. We shall note absence in the Eq.27 elastic forces which is determined returned a particle in initial position, causing its oscillation around of a point of balance.
The Eq.27 is the equation to which at absence of stochastic function F complies with a solving 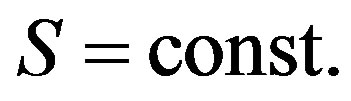 i.e. at
i.e. at 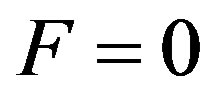 the particle can steadily be in any positionindifferent balance. The Eq.26 is similar to the Eq.27 at
the particle can steadily be in any positionindifferent balance. The Eq.26 is similar to the Eq.27 at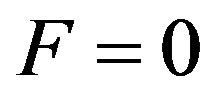 . Function
. Function  complies with the Eq.26, i.e. frequency of allele a is steady at its any value that reflects indifferent character of Hardy-Weinberg balance.
complies with the Eq.26, i.e. frequency of allele a is steady at its any value that reflects indifferent character of Hardy-Weinberg balance.
If there is some stochastic mutagen factor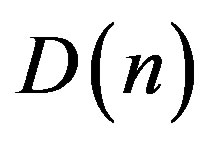 , randomly time-dependent lives of a population (in conditions of a continuous scale of alternation of generations) the Eq.26, by analogy with (27), it is necessary to copy as:
, randomly time-dependent lives of a population (in conditions of a continuous scale of alternation of generations) the Eq.26, by analogy with (27), it is necessary to copy as:
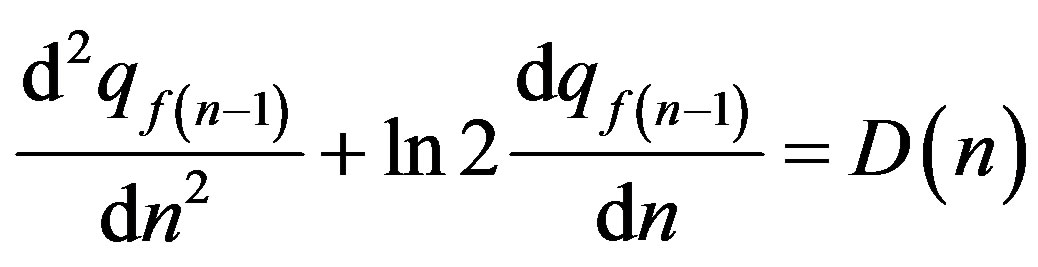 (28)
(28)
Using the result for the first time received by Einstein [3] for the Brownian motion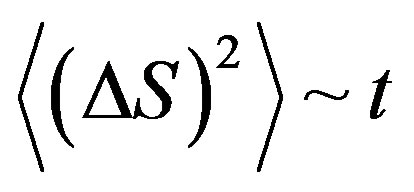 , we shall note that an average square of a deviation of the allele frequency from norm (25) at action on a population of the stochastic mutagen factor proportionally time of a life of a population
, we shall note that an average square of a deviation of the allele frequency from norm (25) at action on a population of the stochastic mutagen factor proportionally time of a life of a population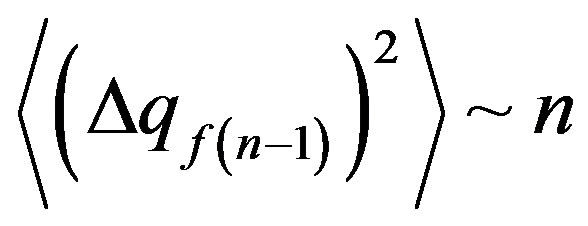 . Angular brackets mean averaging on individuals of a population.
. Angular brackets mean averaging on individuals of a population.
Thus, during a life of a population at action of the stochastic mutagen factor a root mean square deviation of the allele frequency from norm proportionally to a root square from time of a life of a population
 . At the certain level the root mean square deviation of allele frequency from norm can lead to a lethal outcome. For a separate individual a lethal deviation is individually.
. At the certain level the root mean square deviation of allele frequency from norm can lead to a lethal outcome. For a separate individual a lethal deviation is individually.
5. CANCEROGENES AS THE STOCHASTIC MUTAGEN FACTOR
The received result shows, that during a life of a population and alternation of generations at action of the stochastic mutagen factor death rate inevitably grows (similarly to displacement of the Brownian particles from a point of initial supervision). This conclusion has completely general biology-mathematical character.
As the stochastic mutagen factor it is possible to use cancerogenes. The matter is that among other kinds of diseases occurrence of the newgrowths has some features. First of all, it is the big variability of a newgrowths site. It can practically arise in any place of an organism. Besides for oncological diseases typically a variety of factors of cancerogenes: the poor-quality food, the polluted environment, a way of life and professional work, smoking, high-frequency electromagnetic radiations and many other things.
All these cancerogenic factors, finally, affect the reproductive-genetic function of a cell causing its malignant transformation. Is generalized we shall consider, that set of the reasons resulting to occurrence of malignant newgrowths is an influence on an organism of some stochastic mutagen factor.
Despite of stochastic character of influence, it is difficult to present a situation at which the given stochastic mutagen factor completely would be absent. It concerns even completely isolated primitive societies. Especially such factor in any kind always is present at a modern civilized society.
On Figure 2 dynamics death rates (mortality rate coefficient) of the population in the various countries from newgrowths is shown [4]. A mortality rate coefficient this ratio of quantity of died people in the country for a year to an average number of population in the given year multiplied on 1000.
Time interval of 20 years during which death rate was investigated is small term but it is possible to make some conclusions.
In two countries Japans and Canada the law: death rate  is obviously observed. Distinctive feature of these countries is, first, very high level of medicine second, high uniformity of the population which is almost without exception uses these achievements of medicine. Some other social factors determining as a whole a posi-
is obviously observed. Distinctive feature of these countries is, first, very high level of medicine second, high uniformity of the population which is almost without exception uses these achievements of medicine. Some other social factors determining as a whole a posi-

Figure 2. Dynamics of the population death rates (mortality rate coefficient) in the various countries from the newgrowths [4].
tive psychological climate in these countries influence also. In other words, the situation with detection at the earliest stage and treatment of the newgrowths in these countries has approached to the stationary limit on the given level of development of the country. The not changes in this direction, the law-death rate 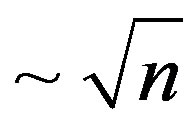 therefore is carried out. The further decrease in death rate will take place at occurrence and universal application of essentially new methods of diagnostics and treatment of a cancer. In the given countries death rate from newgrowths is the basic natural factor of alternation of generations.
therefore is carried out. The further decrease in death rate will take place at occurrence and universal application of essentially new methods of diagnostics and treatment of a cancer. In the given countries death rate from newgrowths is the basic natural factor of alternation of generations.
For other countries, first, the big heterogeneity of the population, second, high immigration of the population which gradually joins modern medicine that conducts or to decrease in the general death rate from newgrowths (USA, Great Britain), or to its invariance (Germany, Russia, France) is characteristic. As a whole it is possible to speak about the general demographic non stationary in these countries.
We speak about dynamics of death rate, instead of about its absolute value which analysis is not the purpose of article. Absolute value of death rate in many countries is frequently defined not natural, but social factors.
The attention an example of Italy for which the lawdeath rate  is carried out with periodic fluctuations. Apparently, it is connected by that Italy is basically the transit state for immigrants. However arising due to change of rules, the delay of immigrants in the country results in fluctuations of a death rate on a background of the law of death rate
is carried out with periodic fluctuations. Apparently, it is connected by that Italy is basically the transit state for immigrants. However arising due to change of rules, the delay of immigrants in the country results in fluctuations of a death rate on a background of the law of death rate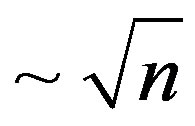 .
.
6. CONCLUSIONS
For the description of a population, it is necessary to use Hardy-Weinberg law, writting down for a continuous scale of alternation of generations.
During a life of a population at action of the stochastic mutagen factor root mean square deviation of allele frequency from norm proportionally to a root square from time of a life of a population.
At action of the stochastic mutagen factors resulting in occurrence of the newgrowths, death rate of the population in the country is proportional to a root square of time of a life of a population only at demographic stationary, i.e. in case of uniformity of the population and the high level of development of medicine accessible to all population. In such countries death rate from oncological diseases has a role of the natural factor of alternation of generations.
Demographic non stationary, first of all, was connected to immigration, results or in decrease in death rate of the population from the newgrowths, or to its invariance.
REFERENCES
- Vogel, F. and Motulsky A. (1990) Human genetics. SpringerVerlag, Berlin.
- Volobuev, A.N. and Petrov, E.S. (2011) Modelling of the populating development of the genome in the radiation of the environment. Natural Science, 3, 1029-1033. doi:10.4236/ns.2011.312128
- Matveev, A.N. (1981) Molecular physics. High School, Moscow.
- Kalabekov, I.G. (2010) Russian reforms in digits and facts. (2010) RUSAKI, Moscow.

