Natural Science
Vol.4 No.1(2012), Article ID:16587,10 pages DOI:10.4236/ns.2012.41008
Electromagnetic nature of the nuclear forces and a toroid model of nucleons in atomic nuclei
![]()
Plovdiv University “P. Hilendarski”, Plovdiv, Bulgaria; *Corresponding Author: kolikov@uni-plovdiv.bg
Received 23 July 2011; revised 15 October 2011; accepted 14 November 2011
Keywords: Strong Interaction; Nucleon; Binding Potential Energy; Electromagnetic Interaction
ABSTRACT
In this paper we consider nucleons as tori, rotating with a constant angular velocity around the straight line passing through their mass centre (geometric centre) and perpendicular to their plane of rotation. We theoretically determine the corresponding potential energy and the force of interaction between pairs of nucleons, using our precise analytical formulas for the electrostatic interaction between two spheres with arbitrary radii and charges, which we derive using experimentally obtained results for the radii and the masses of the nucleons. From the values for binding energy found through our method, it follows that nuclear forces are electromagnetic in nature. In terms of magnitude of the force of interaction between proton and neutron, we obtain that Coulomb’s forces are shortrange. Our toroid model explains the experimental results not only for binding energy, but also for the radius, magnetic moment and the spin of the nuclei of atoms.
1. INTRODUCTION
Modern physics assumes that exist four types of fundamental interactions: strong (nuclear), electromagnetic, weak (leptonic) and gravitational.
The strong interaction is believed not to be electromagnetic by nature, a number of reasons have being brought to bear. But despite of the already century-long history of studying the nuclear interaction and atomic nuclei, even today theoretical nuclear physics has no knowledge about the exact law of interaction between nucleons. At present, the study of the proton and neutron structure and how they interact is one of the most actively developing areas of nuclear physics. However, it is based mainly on the accumulation and the classification of experimental data.
A complete theory of the nucleus has not yet been created, which could explain its structure and all its properties as well as the available experimental data concerning its behaviour [1-4]. The main difficulty here is insufficient knowledge of the forces of interaction between the nucleons, as well as of their structure.
In this article we find out that strong interactions are electromagnetic by nature. Our results are in agreement with the idea of “The Great Unification” of the four types of interactions known. In this aspect, electromagnetic and weak interactions have already been unified in the so-called “electroweak” interactions by A. Salam [5], S. Weinberg [6], and S. Glashow [7] in 1967-1968.
From the perspective of contemporary ideas both the proton and neutron have an internal electric structure. The proton has an electric charge. The neutron, although it can be assumed electrically neutral, i.e. with a common charge , also has an internal electric structure, its negative charge, as opposed to the positive one is distributed primarily at its surface [8,9].
, also has an internal electric structure, its negative charge, as opposed to the positive one is distributed primarily at its surface [8,9].
In the so far created numerous nuclear models it is assumed that Coulomb’s interaction between nucleons has a very small contribution to the binding energy of the nuclei. But, as also noted by R. Feynman, at distances less than  m either Coulomb’s law does not apply, or electrons and protons are not point charges [10].
m either Coulomb’s law does not apply, or electrons and protons are not point charges [10].
We consider nucleons as spatial-dimensional objectstori, in which their electric charge can be redistributed. (This is not in contradiction with the quark model). Then we can determine the electrostatic interaction between them.
As we know, there are no direct experimental confirmations for the existence of charge independence of nuclear forces. For this we infer from indirect considerations, for example, by comparing the binding energy of mirror nuclei. According to our proposed theory it follows that there is no charge independence. It is also confirmed by the fact that there are no atomic nuclei, consisting only of protons (except protium) or only of neutrons. Between proton and proton (with positive charges), and between neutron and neutron (with negative charges on their surfaces), there are no bound states, because from the electromagnetic point of view identical nucleons repel each other.
In [11] by the method of inverse images we solve analytically the problem of electrostatic interactions between two charged conductive spheres with arbitrary electric charges and arbitrary radii  and
and . As a result, we derive in the most common aspect exact analytical formulas for the magnitude of the force and the potential energy of interaction between them. We also determine the potential in an arbitrary point of the electromagnetic field created by two spheres. From the obtained by us formulas follows Coulomb’s law when
. As a result, we derive in the most common aspect exact analytical formulas for the magnitude of the force and the potential energy of interaction between them. We also determine the potential in an arbitrary point of the electromagnetic field created by two spheres. From the obtained by us formulas follows Coulomb’s law when , i.e. for point charges. These results can also be applied with approximation to aspherical bodies having a single center of symmetry, modeling them as spheres having equivalent surface areas [11].
, i.e. for point charges. These results can also be applied with approximation to aspherical bodies having a single center of symmetry, modeling them as spheres having equivalent surface areas [11].
With the obtained by us general formulas, for the first time it could be found the interaction between two charged spheres, which are situated at very short distance between them. We use these results for finding out the electrostatic interaction between nucleons. Experimentally found radii of the nucleons are on the order of  m [12,13]. That is why we consider the systems of proton-neutron, proton-proton and proton-neutron-proton, being at a distance less than
m [12,13]. That is why we consider the systems of proton-neutron, proton-proton and proton-neutron-proton, being at a distance less than  m from each other. We prove that in terms of size of the force of interaction, Coulomb’s forces, in the pairs proton-neutron, are short-acting. Thus we find that the potential binding energy in the atomic nuclei has electromagnetic nature! We find out also the force of interaction between nucleons-a result obtained for the first time in nuclear physics. We also explain other basic experimental data-stability, radius, magnetic moment and spin, of the nuclei of atoms.
m from each other. We prove that in terms of size of the force of interaction, Coulomb’s forces, in the pairs proton-neutron, are short-acting. Thus we find that the potential binding energy in the atomic nuclei has electromagnetic nature! We find out also the force of interaction between nucleons-a result obtained for the first time in nuclear physics. We also explain other basic experimental data-stability, radius, magnetic moment and spin, of the nuclei of atoms.
In [14] we confirm experimentally established stability, binding energy, magnetic moment and spin of the nuclei of deuterium, tritium, helium 3 and helium 4. In general, we consider that all experimental data on the nuclei of atoms can be interpreted, through the constructed by us Toroid model of nucleons by electromagnetic point of view.
2. METHOD FOR FINDING OUT ELECTROSTATIC INTERACTION BETWEEN TWO CHARGED CONDUCTIVE SPHERES
By the method presented by us in [11], we will represent a part, necessary for accomplishment the further calculations.
Let  and
and  be two electrified (isolated) conductive spheres, with charges
be two electrified (isolated) conductive spheres, with charges ,
,  and radii
and radii ,
,  respectively. Let’s denote with
respectively. Let’s denote with  the distance between their centres
the distance between their centres ,
,  in an inertial system
in an inertial system  (Figure 1). Since charges
(Figure 1). Since charges  and
and  are evenly distributed on the surfaces of
are evenly distributed on the surfaces of  and
and , it is generally assumed that before the interaction between the spheres they are concentrated in centres
, it is generally assumed that before the interaction between the spheres they are concentrated in centres  and
and  respectively.
respectively.
As a result of the electrostatic interaction between 
and , on their surfaces appear induced charges
, on their surfaces appear induced charges  and
and , which are interrelated. Formally, we can assume that these charges are located on line segment
, which are interrelated. Formally, we can assume that these charges are located on line segment . On the surfaces of
. On the surfaces of  and
and  are obtained uniformly distributed charges
are obtained uniformly distributed charges  and
and , we can assume that they are concentrated in their centres
, we can assume that they are concentrated in their centres  and
and .
.
From the law for preservation of electric charge the equations  and
and  are in power, i.e.
are in power, i.e.
 and
and (1)
(1)
By the method of image charges, we determine the charges ,
,  and hence the charges
and hence the charges ,
, . Let as a consequence of
. Let as a consequence of  be generated image charges
be generated image charges 
 Because each charge
Because each charge  generates
generates  , the charges with an odd index
, the charges with an odd index 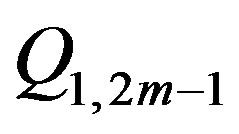
 are located in the sphere
are located in the sphere , and charges with an even index
, and charges with an even index —in the sphere
—in the sphere . Similarly are determined the image charges
. Similarly are determined the image charges 
 , arising as a consequence from charge
, arising as a consequence from charge . The charges with an odd index
. The charges with an odd index 
 are located in the sphere
are located in the sphere , and charges with an even index
, and charges with an even index —in the sphere
—in the sphere .
.
Let’s denote  and
and . We introduce for
. We introduce for  the following denotations:
the following denotations:
 (2)
(2)
If  are the distances of image-charges
are the distances of image-charges , respectively to the centers of the spheres
, respectively to the centers of the spheres , in [11] we obtain that:
, in [11] we obtain that:
 (3)
(3)
We find also that:

Figure 1. Electrostatic interaction between two charged conductive spheres S1 and S2.
 (4)
(4)
Lets
 (5)
(5)
where  at
at 
 .
.
Since charges  and
and  are sums of all image charges, located respectively in the spheres
are sums of all image charges, located respectively in the spheres  and
and , then
, then
 and
and  .
.
From here and from (5) and (6) it follows that  and
and . Then, substituting these equations in (1), we get:
. Then, substituting these equations in (1), we get:
 (6)
(6)
Let denote the charges from Formulae (4) and (6), which are located in the sphere  with
with , and these which are located in the sphere
, and these which are located in the sphere  with
with 
 Thus
Thus ;
; , and for
, and for ,
,  ,
, ;
; ,
,  (Figure 1). Their corresponding distances to the centers of the spheres, where they are situated we denote with
(Figure 1). Their corresponding distances to the centers of the spheres, where they are situated we denote with  and
and 
 , where
, where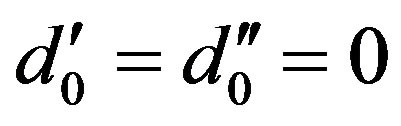 .
.
If , and
, and , then, according to Coulomb's law, for the magnitude
, then, according to Coulomb's law, for the magnitude  of the projection of the force of interaction on
of the projection of the force of interaction on , acting on spheres
, acting on spheres  and
and , we obtain
, we obtain
 . (7)
. (7)
The potential energy of interaction between the two spheres  and
and , according to [15], is
, according to [15], is
 . (8)
. (8)
Let us point out that in (7) and (8) we do not take into consideration the interactions between the charges inside the spheres  and
and  as actually the interaction is outer-between the charges on the surface of
as actually the interaction is outer-between the charges on the surface of  with the charges on the surface of
with the charges on the surface of .
.
Let  be an arbitrary point in the electric field created by charges
be an arbitrary point in the electric field created by charges  and
and 
 . If
. If  is at distances
is at distances  and
and  from charges
from charges  and
and  respectively (Figure 1), then, using the metric relationships in a triangle, we can determine
respectively (Figure 1), then, using the metric relationships in a triangle, we can determine

and
 .
.
Then based on the principle of linear superposition of states, the potential at point  will be the sum of the potentials of all charges in
will be the sum of the potentials of all charges in  [15]. Therefore
[15]. Therefore
 . (9)
. (9)
3. MODELS OF THE NUCLEONS
In the field of elementary particles there are two leading models: standard and helicon.
The standard model [16-18] presents elementary particles as quantum objects that can be both wave and particle. As particles they have mass, charge, spin, magnetic moment, quadrupole moment. The elementary particles mainly are modelling with spheres.
There are three groups of standard models of the atomic nucleus. However, each of them can explain only a part of its properties and cannot explain the others. The physics concepts which are in the base of these models are different, and sometimes they are even contrary. For example in some models it is assumed that there are strong interactions between nucleons, but according to others they do not interact at all.
The helicon model [19-22], or ring model is less wellknown. According to that model the particles have ring spiral structure of charged filaments, one or more. The filaments are superconductors coiled around an imaginary ring. The helicon model is consistent with all the widely accepted and experimentally verified properties of elementary particles. This model implies the assumption that all known types of interactions (strong, electroweak, gravitational) should be electromagnetic in nature.
The toroid model of the nucleons, represented by us, is to a certain degree in contradiction with the standard model, but it is in full agreement with the helicon model.
In [23] we model the proton with an electrically charged sphere with radius , which rotates with a constant angular velocity about an axis
, which rotates with a constant angular velocity about an axis , passing through the geometrical center of mass of the proton perpendicular of rotating plain. On the basis of that we determine theoretically the magnetic moment
, passing through the geometrical center of mass of the proton perpendicular of rotating plain. On the basis of that we determine theoretically the magnetic moment  of the proton. We use experimentally obtained results for
of the proton. We use experimentally obtained results for  JT–1 [24] and for his radius
JT–1 [24] and for his radius  m [25], we calculate the magnitude of linear velocity
m [25], we calculate the magnitude of linear velocity  ms–1 of the points of the “equatorial” circle
ms–1 of the points of the “equatorial” circle  of the proton. Then, because of the huge velocity of
of the proton. Then, because of the huge velocity of —on order of relativity, the proton should be stretched in the direction of “equatorial” circle, i.e. it should have an ellipsoidal shape. Besides of that the electrical charge of the proton in its center is equal to zero and the quadrupole moments are also equal to zero, i.e. the distributed charge in the proton is centrally symmetrical [26]. On basis of this we can consider the nucleons as tori.
—on order of relativity, the proton should be stretched in the direction of “equatorial” circle, i.e. it should have an ellipsoidal shape. Besides of that the electrical charge of the proton in its center is equal to zero and the quadrupole moments are also equal to zero, i.e. the distributed charge in the proton is centrally symmetrical [26]. On basis of this we can consider the nucleons as tori.
We consider the nucleons as tori, rotating with a constant angular velocity around a straight line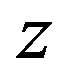 , passing through their mass (geometrical) center
, passing through their mass (geometrical) center  and perpendicular to their plane of rotation (Figure 2). The idea the nucleons to be modeling with tori can be found in [27].
and perpendicular to their plane of rotation (Figure 2). The idea the nucleons to be modeling with tori can be found in [27].
Furthermore, using the results of Section 2, we will find the interactions between the nucleons in the common standard model and in our toroid model. For this purpose we consider an arbitrary inertial reference system  in a flat physical 3-dimensional space. We assume that there is no electromagnetic radiation from the nucleons in the inertial system
in a flat physical 3-dimensional space. We assume that there is no electromagnetic radiation from the nucleons in the inertial system , because there is no such radiation at the permissible energy quantum orbits in Niels Bohr’s sense.
, because there is no such radiation at the permissible energy quantum orbits in Niels Bohr’s sense.
To define the interaction between the nucleons we will consider them as dimensional objects, in which the charge can be redistributed. The charge of the proton is  C, and the total charge of the neutron is
C, and the total charge of the neutron is  C [24].
C [24].
Due to the mass defect in the nucleus, the potential energy of the interaction in the atoms’ nuclei calculates by the following formula [2]:
 . (10)
. (10)
Here  is the number of the protons,
is the number of the protons, —number of the neutrons;
—number of the neutrons;  ms−1 is the velocity of the light in flat vacuum;
ms−1 is the velocity of the light in flat vacuum;  kg and
kg and  kg are the masses of the proton and of the neutron, respectively [24] and
kg are the masses of the proton and of the neutron, respectively [24] and  is the mass of the considered nucleus. We will find the values of
is the mass of the considered nucleus. We will find the values of  according to our method with Formula (8), comparing them with the values obtained through Formula (10).
according to our method with Formula (8), comparing them with the values obtained through Formula (10).

Figure 2. Toroid model of nucleon.
4. FINDING OUT THE INTERACTION BETWEEN THE NUCLEONS IN THE STANDARD MODEL
In this Section we consider the nucleons as spheres, as they are represented in the standard model.
1) Let proton and neutron are imaginary spheres respectively  and
and , as
, as  is with the charge
is with the charge , and
, and  is with the charge
is with the charge . For simplicity, we assume that as spheres the radii of the proton and neutron are equal, i.e.
. For simplicity, we assume that as spheres the radii of the proton and neutron are equal, i.e. . We assume that the distance between
. We assume that the distance between  and
and  is
is  m, i.e. that the distance between their centres
m, i.e. that the distance between their centres  and
and  is
is  .
.
The experimentally obtained radii of the proton and neutron are  m [12,13,24-26]. Then at different values of
m [12,13,24-26]. Then at different values of  m
m  m, by formulas (7) and (8) we find the following results, represented in Tables 1 and 2.
m, by formulas (7) and (8) we find the following results, represented in Tables 1 and 2.
The data in Table 1 show that  when
when  m assumes values around the known binding energy
m assumes values around the known binding energy  J in the deuteron, determined by the Formula (10). These values for
J in the deuteron, determined by the Formula (10). These values for  and
and  increase if
increase if  m. This indicates that at sufficiently small distances between nucleons nuclear forces could be comparable to coulomb’s forces!
m. This indicates that at sufficiently small distances between nucleons nuclear forces could be comparable to coulomb’s forces!
The data in Table 2 show that at distances  m between
m between  and
and  the forces of interaction between the point charge
the forces of interaction between the point charge  in the centre of
in the centre of  and the sphere
and the sphere  are much smaller in absolute value than those between the two spheres
are much smaller in absolute value than those between the two spheres  and
and . The difference for
. The difference for  is about one order, and for
is about one order, and for  is about two orders. Thus at distances smaller than 10−16 m the proton should not be considered as point charge!
is about two orders. Thus at distances smaller than 10−16 m the proton should not be considered as point charge!
2) Let now two protons are imaginary spheres  and
and , with charges
, with charges . We assume that the distance between
. We assume that the distance between  and
and  is again
is again  m, i.e. that the distance between their centres
m, i.e. that the distance between their centres  and
and  is
is .
.
Because the experimentally obtained radius of the proton is  m, then at different values of
m, then at different values of , by Formulae (7) and (8) we find the following results, represented in Tables 3 and 4.
, by Formulae (7) and (8) we find the following results, represented in Tables 3 and 4.
Comparing the data in Tables 3 and 4, we see that with an approximation we can calculate the potential energy between two protons as we model them by point charges, especially when  is on the order of
is on the order of 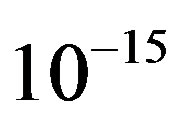 m.
m.
3) Let two protons and one neutron be imaginary spheres, denoted respectively by ,
,  and
and . The distance between
. The distance between  and
and  is
is  and the distance between each of them and
and the distance between each of them and  is
is  . The centers of the three spheres in Figure 3 may or may not lay on a straight line.
. The centers of the three spheres in Figure 3 may or may not lay on a straight line.
Let  m. The interaction between
m. The interaction between  and
and , based on the conclusions in 2), we calculate with some approximation (reducing the potential energy and the force of attraction), with the interaction between point charges
, based on the conclusions in 2), we calculate with some approximation (reducing the potential energy and the force of attraction), with the interaction between point charges , situated in the centers of the spheres
, situated in the centers of the spheres  and
and . Thus we obtain the following results presented in Table 5.
. Thus we obtain the following results presented in Table 5.

Table 1. The binding energy and force of interaction between the spheres Sp and Sn.

Table 2. The binding energy and the force of interaction between point charge p, which is in the centre of Sp, and the sphere Sn.

Table 3. The binding energy and the force of interaction between the spheres Sp1 and Sp2.

Table 4. The binding energy and the force of interaction between two point charges p in the centres of the spheres Sp1 and Sp2.

Figure 3. Position of the three spheres Sp1, Sp2 and Sn.

Table 5. Binding energy and force of interaction between the spheres Sp1, Sp2 and Sn.
The data at  m can be obtained doubling the result from Table 1 and adding the corresponding data from Table 4. In case of one proton and two neutrons the result with an approximation is obtained, through doubling of the data from Table 1. More complex systems of nucleons, modeled with spheres, can be considered analogically!
m can be obtained doubling the result from Table 1 and adding the corresponding data from Table 4. In case of one proton and two neutrons the result with an approximation is obtained, through doubling of the data from Table 1. More complex systems of nucleons, modeled with spheres, can be considered analogically!
Our verification shows that even when  m we could not reach the well-known binding energies of the helion
m we could not reach the well-known binding energies of the helion  and of the triton
and of the triton  J, determined by the Formula
J, determined by the Formula
(10). With the standard model it can be hard to explain and the experimentally obtained magnetic moments of the nuclei of the atoms, toward magnetic moments of their consisting nuclei. It can be hard to explain experimentally obtained results for the radii and the stability of the nuclei.
Therefore we suggest the toroid model.
5. FINDING OUT THE INTERACTION BETWEEN THE NUCLEONS IN THE TOROID MODEL
We consider the nucleons as tori (Figure 2).
Let proton and neutron are two tori, accordingly  and
and , as
, as  is with charge
is with charge , and
, and  is with charge
is with charge . The centers of the tori we denote with
. The centers of the tori we denote with  and
and . We also assume that the central circles of
. We also assume that the central circles of  and
and  lie in parallel or coincident planes and rotate in one and the same or different directions with constant angular velocity around a straight line
lie in parallel or coincident planes and rotate in one and the same or different directions with constant angular velocity around a straight line  passing through
passing through  and
and , and perpendicular to the plane of their rotation. So if
, and perpendicular to the plane of their rotation. So if , then
, then .
.
Let us denote by  and
and  the centres of the forming circles of the tori
the centres of the forming circles of the tori  and
and , and with
, and with  and
and —the radii of the central circles of
—the radii of the central circles of  and
and . We assume that
. We assume that  and
and  are at a distance
are at a distance  from each other.
from each other.
Because of that

and the tori rotate with a constant angular velocity , in the result of centrifugal forces the radius of the proton
, in the result of centrifugal forces the radius of the proton  will be smaller than the radius of the neutron
will be smaller than the radius of the neutron . For determination we will use the experimental data for
. For determination we will use the experimental data for  m [25] and for
m [25] and for  m [26]. From
m [26]. From  it follows
it follows  (Figure 4).
(Figure 4).
Let  and
and  be the radii of the forming circles of
be the radii of the forming circles of  and
and . It is clear that
. It is clear that , and
, and . Besides that
. Besides that
 and
and (11)
(11)
Let us denote with  the radius of the circle of the empty part of the circle with a radius
the radius of the circle of the empty part of the circle with a radius . Then
. Then
 . (12)
. (12)
We assume that the volume mass densities of the proton and neutron are equal, i.e. . The volumes of the tori
. The volumes of the tori  and
and , according to [28], are correspondingly
, according to [28], are correspondingly  and
and . Then from
. Then from
 it follows that
it follows that
 . (13)
. (13)
In (13), we substitute the experimentally measured masses of the proton and the neutron, without regard to the mass defect, because we do not consider the specific nucleus.
From geometrical considerations for , the following equation is satisfied:
, the following equation is satisfied:
 . (14)
. (14)
Due to the central symmetry of the proton charge [26], we may assume that all its charge  is concentrated in the geometric centre
is concentrated in the geometric centre  of the torus
of the torus .
.

Figure 4. Cross section of a proton-neutron system.
In order to apply the results from Section 2 for spheres we will remodel the tori. We will emphasize that the potential energy and the force of interaction between two spheres depend on the distance between image-charges, i.e. from the lengths of the line segments 
 by Formula (3). These lengths in (3) are determined from the squares of the radii
by Formula (3). These lengths in (3) are determined from the squares of the radii  or
or  of the spheres and from the length of their central line
of the spheres and from the length of their central line , where
, where  is the smallest distance between their surfaces. For the square of the radii of each of the two spheres, it is satisfied
is the smallest distance between their surfaces. For the square of the radii of each of the two spheres, it is satisfied ,
,  , where
, where  is the surface area of the corresponding sphere. Therefore, when we remodel the tori we have to keep both the faces
is the surface area of the corresponding sphere. Therefore, when we remodel the tori we have to keep both the faces  and
and  of their surface areas and the distances
of their surface areas and the distances  between them.
between them.
We remodel the proton as a sphere , with radius
, with radius  whose centre
whose centre  is situated on the straight line
is situated on the straight line . The sphere surface area is equivalent to the torus surface area, i.e. it has the same surface area as the torus
. The sphere surface area is equivalent to the torus surface area, i.e. it has the same surface area as the torus . (According to the results of 1) we cannot consider
. (According to the results of 1) we cannot consider  as a point, because the proton and the neutron are separated by a distance
as a point, because the proton and the neutron are separated by a distance  m).
m).
The area of the surface  of a torus
of a torus  according to [28] is
according to [28] is
 . (15)
. (15)
Then, as the areas of the surfaces of the torus  and of the sphere
and of the sphere  are equal, (15) implies that the radius of
are equal, (15) implies that the radius of  is
is
 . (16)
. (16)
Further we will remodel and the neutron and will consider two cases.
1) We remodel the neutron  with a sphere
with a sphere  with a radius
with a radius  and a center
and a center  on the straight line
on the straight line , that is an equivalent in face on its surface. At that
, that is an equivalent in face on its surface. At that  and
and  are positioned at a distance
are positioned at a distance  m between them.
m between them.
For selected values of , from Formulae (11)-(13) we find out
, from Formulae (11)-(13) we find out ,
,  ,
,  and
and . From here and from Formula (16) we obtain the radius
. From here and from Formula (16) we obtain the radius  of
of  and analogically the radius
and analogically the radius  of the sphere
of the sphere .
.
Then, at different values of  and
and , from Formulae (7) and (8), we obtain the following results presented in Table 6.
, from Formulae (7) and (8), we obtain the following results presented in Table 6.
The data in Table 6 show that the values of the binding energy in atomic nuclei can be obtained by means of electromagnetic interactions between their nucleons, varying  and
and ! For
! For , as well as when values of
, as well as when values of  approach the values of
approach the values of , the binding energy increases. Thus, the remodeling of the tori
, the binding energy increases. Thus, the remodeling of the tori  and
and  with spheres
with spheres  and
and , reduce the values of
, reduce the values of  and
and , because the surface areas of interaction between them are reduced and the distances between the charge-images in
, because the surface areas of interaction between them are reduced and the distances between the charge-images in  and
and  are increased.
are increased.

Table 6. Binding energy and force of interaction between the tori Tp and Tn, remodeled with spheres of equivalent surfaces Sp and Sn.
Therefore we apply a more adequate to the reality approach for finding  and
and .
.
2) We remodel the neutron  as a torus
as a torus  that is equivalent in surface area. At that
that is equivalent in surface area. At that  and
and  have the same centres
have the same centres  and
and , and are positioned at the same distance
, and are positioned at the same distance  between them—as
between them—as  and
and  (Figure 5).
(Figure 5).
Let  be a sphere. Its central circle, is forming for the torus
be a sphere. Its central circle, is forming for the torus . We denote the centre of
. We denote the centre of  with
with , at that
, at that  and with
and with —the radius of
—the radius of . From the equality of the surface areas
. From the equality of the surface areas  and
and  of the tori
of the tori  and
and , as in (15), it follows that
, as in (15), it follows that
 . (17)
. (17)
If , then
, then . From
. From  we obtain, that
we obtain, that , i.e.
, i.e.
 . (18)
. (18)
For the number l of spheres  which have total surface area equal to the surface area of the torus
which have total surface area equal to the surface area of the torus  is fulfilled
is fulfilled . Therefore
. Therefore
 . (19)
. (19)
We assume that the centre  is motionless relative to the inertial reference system J. We introduce solid non-inertial reference system
is motionless relative to the inertial reference system J. We introduce solid non-inertial reference system  that rotates with constant angular velocity
that rotates with constant angular velocity  of rotation of
of rotation of  in relation to J. At that, the point
in relation to J. At that, the point  is the centre of the coordinate system
is the centre of the coordinate system  , stationary connected with
, stationary connected with  and related to which the spheres
and related to which the spheres  and
and  are motionless to each other (Figure 5).
are motionless to each other (Figure 5).

Figure 5. Cross section of reduced model of the proton-neutron system.
Giving values to  and
and , from Formulae (11)-(14) we find
, from Formulae (11)-(14) we find ,
,  ,
,  ,
,  and
and . From here and from Formulae (16)-(18), we find the radius
. From here and from Formulae (16)-(18), we find the radius  of the sphere
of the sphere  and radius
and radius  of the “forming sphere”
of the “forming sphere” .
.
Thus at , through Formulae (7) and (8), we find the binding energy
, through Formulae (7) and (8), we find the binding energy  and force of interaction
and force of interaction . According to (19), the binding energy
. According to (19), the binding energy  and force of interaction
and force of interaction  between a proton and neutron will be
between a proton and neutron will be
 and
and
 . (20)
. (20)
The Equation (20) are valid because the forming spheres of the torus  are situated symmetrically relative to the centre of the sphere
are situated symmetrically relative to the centre of the sphere .
.
At different values of  and
and  we find the following results presented in Table 7.
we find the following results presented in Table 7.
The obtained huge values for the binding energy and the force of interaction between the proton and neutron demonstrates that nuclear forces are electromagnetic!
The results for configurations of two protons and one neutron, one proton and two neutrons, etc. are derived by analogy as we showed in 3).
With Formula (9) we can find the potential of electromagnetic field in a given point  outside the tori and the spheres that we use for modeling the nucleons. This way we can seek the quadrupole moments of the atomic nuclei.
outside the tori and the spheres that we use for modeling the nucleons. This way we can seek the quadrupole moments of the atomic nuclei.
6. MAIN CHARACTERISTICS OF THE NUCLEI IN THE TOROID MODEL
Due to the larger surfaces of the tori and the larger areas with which they interact relative to the spheres, we obtain larger values for the binding energy and force of interaction between tori. This can be seen when comparing data from Tables 1, 6 and 7.
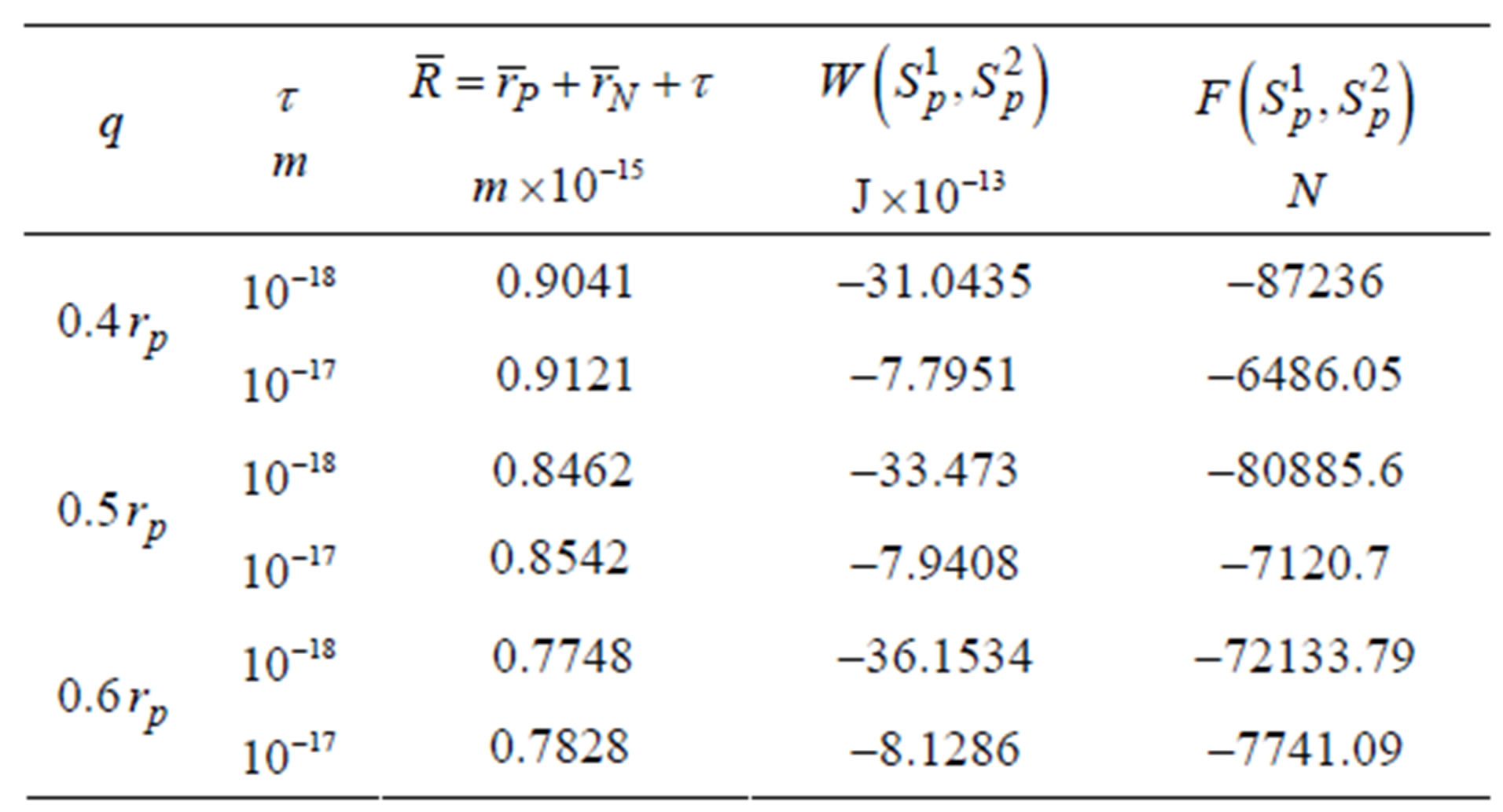
Table 7. Binding energy and force of interaction between the tori Tp and Tn, remodeled correspondingly as equivalent in surfaces sphere SP and torus TN.
In Table 6 we obtain commensurability between nuclear and electromagnetic forces. In Table 7, at distances  m and with only one proton and one neutron we obtain very large absolute values of the binding energy between them:
m and with only one proton and one neutron we obtain very large absolute values of the binding energy between them:  J.
J.
For comparison the binding energy in the main simple nuclei-deuteron, triton, hellion and  -particle we have:
-particle we have:




These values are calculated using Formula (10) taking into account the experimentally obtained masses of these nuclei:
 kg,
kg,  kg,
kg,  kg,
kg,  kg [24].
kg [24].
At that, comparing the data of Tables 1 and 5, it follows that in the proton-neutron-proton system the values for  and F increase. It is clear that these values of the neutron-proton-neutron system will be (with approximation) doubled values of the neutron-proton system. What is more, for
and F increase. It is clear that these values of the neutron-proton-neutron system will be (with approximation) doubled values of the neutron-proton system. What is more, for  m or
m or  the values of the binding energy and interaction force between one proton and one neutron increase.
the values of the binding energy and interaction force between one proton and one neutron increase.
Therefore, by varying  and
and  we can find the binding energy
we can find the binding energy , and from there the force of interaction
, and from there the force of interaction  in different atomic nuclei.
in different atomic nuclei.
We should note that we calculate the force of interaction within atomic nuclei for the first time in atomic physics!
Besides that, the symmetrical positioning of the proton and neutron tori relative to each other corresponding to the minimum of binding energy will ensure stability of the nuclei [14].
When nucleons bind in simple atomic nuclei the masses of the nuclei are larger than the masses of any of the constituting nucleons. Then, as a consequence of the spinning of the nucleons, the centrifugal force caused by the corresponding mass increases and the radii of the nuclei increase relative to those of the nucleons. This is why the experimentally determined radii of the deuteron, triton, hellion and  -particle are correspondingly
-particle are correspondingly
 m [24],
m [24],  m [29],
m [29],  m and
m and  m [30].
m [30].
Here, as with the proton, we assume that the charge radius and the mass radius are equal since they are not significantly different [2].
As a consequence of the centrifugal forces the proton and the neutron tori are disproportionately “stretched”. This stretching, as well as the positioning of the nucleons relative to each other, explains the magnetic moment of the nuclei relative to those of the separate nucleons in their spinning in the same or different directions. The magnetic moment of the proton is  and of the neutron is
and of the neutron is  [24] while the magnetic moments of the deuteron, triton, hellion and
[24] while the magnetic moments of the deuteron, triton, hellion and  -particle are correspondingly:
-particle are correspondingly:


 and
and .
.
The spins of the nucleons are equal to . If the central circles of their tori lie in coplanar planes, then the spinning of their tori in the same or opposite directions determines the corresponding spins of the nuclei. Because of that, these spins are equal to
. If the central circles of their tori lie in coplanar planes, then the spinning of their tori in the same or opposite directions determines the corresponding spins of the nuclei. Because of that, these spins are equal to , where
, where  is a certain whole number [2].Thus the spins of the deuteron, triton, hellion and
is a certain whole number [2].Thus the spins of the deuteron, triton, hellion and  -particle are
-particle are ,
,  ,
,  and
and , as it was experimentally determined [2].
, as it was experimentally determined [2].
7. DISCUSSION
In [11] we for the first time obtained in the general aspect the exact analytical formulas for the determination of the electrostatic interaction between two charged conducting spheres. At that, this method can be used if the non-intersecting spheres have any sized radii and are at any distance between their centers.
A number of authors until now have derived some specific cases or approximate formulas [31-35]. However with the formulas obtained by them it is not possible to determine exactly the binding energy and force of interaction between two spheres, especially if they are very close to each other. Precisely because of that we obtain that the strong interactions have an electromagnetic nature—by looking at nucleons at distances  m! Thus we also confirm the conclusion of R. Feynman [10] that nucleons at these distances should not be considered as point charges.
m! Thus we also confirm the conclusion of R. Feynman [10] that nucleons at these distances should not be considered as point charges.
The toroid model of nucleons that we created, based on which we derive that strong interactions are electromagnetic, is a new idea in nuclear physics. Using that idea it is possible to obtain the main characteristics of nuclei in good agreement with the experimentally obtained values as we have showed for the deuteron, triton, hellion and  -particle [14].
-particle [14].
We consider that our model can confirm with good accuracy all the main experimental values for atomic nuclei!
8. CONCLUSION
Our research concerns such an area of knowledge, which is fundamental to understanding the structure of matter and its properties. These studies concern the fundamental science and its application. The practical consequences from the understanding of the strong interactions and the essence of the nucleons in the atomic nucleus will contribute for directing of the experimental researching for the solving of energetic problem and nuclear safety.
9. ACKNOWLEDGEMENTS
The authors express their gratitude to the computer specialist Stefan Bozhkov, who with the help of Wolfram Mathematica 7.0 performs the calculations in this article. The results of the present studies are published with the financial support of the Fund for Scientific Research with the Ministry of Education and Science under contract DTK No. 02/35.
REFERENCES
- Cook, N. (2006) Models of the atomic nucleus. Springer, Berlin.
- Krane, K. (1999) Introductory nuclear physics. WileyVCH, Hoboken.
- Martin, B. (2008) Nuclear and particle physics. 3th Edition, Wiley, Hoboken.
- Schopper, H., Altarelli, G., Grünewald, M. and Inoue, K. (2008) Elementary particles. Springer, Berlin.
- Salam, A. (1968) Weak and electromagnetic interactions. In: Svartholm, N., Ed., Elementary Particle Physics, Stockholm, 367.
- Weinberg, S. (1967) A model of leptons. Physical Review Letters, 19, 1264-1266. doi:10.1103/PhysRevLett.19.1264
- Glashow, S.L. (1979) Towards a unified theory—Threads in a tapestry. http://www.nobelprize.org/nobel_prizes/physics/laureates/1979/glashow-lecture.pdf
- Hofstadter, R. (1956) Electron scattering and nuclear structure. Reviews of Modern Physics, 28, 214-2554. doi:10.1103/RevModPhys.28.214
- Burcham, W.E. (1963) Nuclear physics. McGraw-Hill book Co., Inc., San Francisco.
- Feynman, R. (1964) The Feynman lectures on physics: Exercises. Addison Wesley Publishing Co., Boston.
- Kolikov, K., Ivanov, D., Krustev, G., Epitropov Y. and Bozhkov, S. (in press) Electrostatic interaction between two conducting spheres. Journal of Electrostatics.
- Christensen, J. (1990) The structure of an atom. Wiley, London.
- Brown, J. (1980) The physical science encyclopedia. Cornell University Press, New York.
- Кolikov, K., Ivanov, D. and Кrustev, G. (2011) Electromagnetic nature of the nuclear forces and a toroid model of nucleons in atomic nuclei. Scientific Research of the Union of Scientists in Bulgaria, Plovdiv, 283-300.
- Halliday, D., Resnick, R. and Walker, J. (2011) Fundamentals of physics. 9th Edition, John Wiley & Sons, Inc., New York.
- Standard model (2011). http://en.wikipedia.org/wiki/Standard_Model.
- University of Tennessee. Standard model (2011). http://electron6.phys.utk.edu/phys250/modules/module%206/standard_model.htm
- Fehling, D. (2011) The standard model of particle physics: A lunchbox’s guide. http://www.pha.jhu.edu/~dfehling/
- Bergman, D. (2000) The real proton. Foundations of Science, 3, 4.
- Toroidal ring model (2011). http://www.enotes.com/topic/Toroidal_ring_model
- Toroidal ring model (2011). http://en.wikipedia.org/wiki/Toroidal_ring_model
- Twain, M. (1995) The undiscovered physics. http://groupkos.com/mtwain/TheProton.pdf.
- Kolikov, K., Krastev, G. and Epitropov, Y. (2010) Theory of the allocation of the electrical charge of the proton and its magnetic moment. Scientific Research of the Union of Scientists in Bulgaria, Plovdiv, 433-439.
- Mohr, P., Taylor, B. and Newell, D. (2008) CODATA recommended values of the fundamental physical constants: 2006. http://arxiv.org/abs/0801.0028.
- Sick, I. (2003) On the rms-radius of the proton. Physics Letters B, 576, 62-67. doi:10.1016/j.physletb.2003.09.092
- Sardin, G. (1999) Fundamentals of the orbital conception of elementary particles and of their application to the neutron and nuclear structure. Physics Essays, 12, 204. doi:10.4006/1.3025378
- Miller, G. (2008) Non-spherical shapes of the proton: Existence, measurement, and computation. Nuclear Physics News, 18, 12-16. doi:10.1080/10506890802123721
- Gellert, W., Kästner, H. and Neuber, S. (1983) Mathematical encyclopedic dictionary. Science and Art, Sofia, 585.
- Kirscher, J., Griesshammer, H., Shukla, D. and Hofmann, H. (2010) Universal correlations in pion-less EFT with the resonating group method: Three and four nucleons. European Physical Journal A, 44, 239-256. doi:10.1140/epja/i2010-10939-5
- Wang, L.-B., Mueller, P., Bailey, K. et al. (2004) Laser spectroscopic determination of the 6He nuclear charge radius. Physical Review Letters, 93, 142501. doi:10.1103/PhysRevLett.93.142501
- Smythe, W. (1968) Static and dynamic electricity, McGraw-Hill, New York.
- Jackson, J. (1998) Classical electrodynamics. Wiley, New York.
- Soules, J. (1990) Precise calculation of the electrostatic force between charged spheres including induction effects. American Journal of Physics, 58, 1195-1199. doi:10.1119/1.16251
- Larson, C. and Goss, E. (1970) A coulomb’s law balance suitable for physics majors and nonscience students. American Journal of Physics, 38, 1349-1352. doi:10.1119/1.1976097
- Slisko, J. and Brito-Orta, R. (1998) On approximate formulas for the electrostatic force between two conducting spheres. American Journal of Physics, 66, 352-355. doi:10.1119/1.18864

