Received 26 May 2014; revised 2 July 2014; accepted 15 July 2014

ABSTRACT

This paper is concerned with the in-plane elastic stability of arches subjected to a radial concen- trated load. The equilibrium equation for pin-ended circular arches is established by using energy method, and it is proved that the axial force is nearly a constant along the circumference of the circular arches. Based on force method, the equation for the primary eigen function is derived and solved, and the approximate analytical solution of critical instability load is obtained. Numerical examples are given and discussed.

Keywords:

In-Plane Elastic Stability, Buckling, Critical Load, Circular Arch, Force Method

1. Introduction

The circular arch structure is widely used in engineering practice, such as roadway supporting of mine engi- neering, highway/railroad bridge and architectural structure, and in-plane elastic stability of arches is one of the most important problems. The classical methods for predicting in-plane buckling loads consider bifurcation from a prebuckling equilibrium path to an orthogonal buckling path, closed from solutions for the classical buckling load for pin-ended and fixed circular arches subjected to a radial load uniformly distributed around the arch axis are given in several publications [1] -[4] . The energy method is widely used to investigate the instability of shallow circular arches subjected to central point loading, to obtain the corresponding approximate closed form solutions [5] . An exact analysis method for shallow circular arches was used to obtain analytical solutions [6] , but limited to fixed ended arches and the solutions for buckling mode were very complicated. A virtual work formulation was used to establish the nonlinear equilibrium conditions and to derive the buckling equilibrium equations for shallow arches, and the approximate analytical solutions were obtained [7] [8] . However, most theoretical stu- dies and the approximate analytical solutions were confined to radial loading uniformly distributed around the arch axis and central point loading. For loading, numerical methods such as finite element methods were often used for the prebuckling linear elastic analysis [9] [10] , and the eigenvalue formulation [11] [12] and the nonli- near formulation [13] were used to determine the buckling loads. The transient analysis method was used to de- termine the buckling loads [14] . Closed form solutions for in-plane elastic buckling of a circular arch subjected to loads are not available and the present paper is devoted to that problem.

In this paper, the in-plane elastic stability of pin-ended circular arches subjected to a concentrated load is ana- lyzed. The virtual work procedure [7] [8] [14] [15] and a force method [16] are used to derive the eigenvalue equation for pin-ended circular arches and to obtain the analytical solutions for engineering applications.

2. Differential Equilibrium Equations of Hinge-Ended Arch

As Figure 1 shows, the O is centre of the circular arch ACB with a radius of R, A and B are the two hinge-ended points, C is the top points of the arch, α is the semi-angle of the arch, P is a radial concentrated load, θ is the an- gle from C to the concentrated load point.

Before buckling occur, the axial strain at any point of the arch can be expressed [1] as

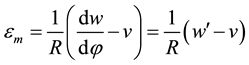. (1)

the axial force can be expressed as

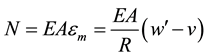. (2)

and the moment can be expressed as

. (3)

Then we have strain energy

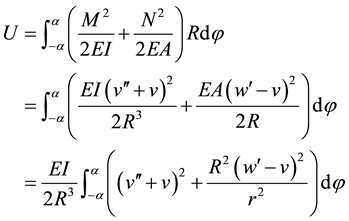. (4)

and the external work

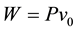. (5)

then we get total potential energy

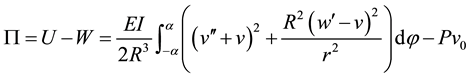. (6)

For the in-plane elastic arches subjected to a pair of concentrated loads, based on the principle of minimum potential energy, then furnishes

. (7)

Integrating Equation (7) by parts leads to

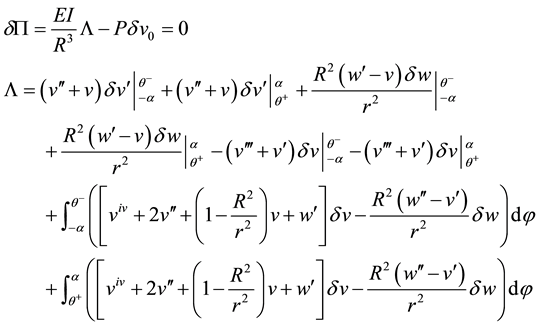. (8)

wherein, 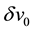is the corresponding virtual radial displacement at the loading point, and 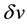are the cor- responding virtual displacements.

Because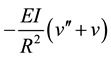, are continuous at, and, , ,

at, so we can simplify Equation (8) as

. (9)

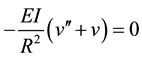from Equation (9), the basic differential equilibrium equations can be obtained as

. (10)

and the force boundary conditions can be obtained as

. (11)

From the first equation of , it follows that

. (12)

where is the axial force in the arch, which means that the axial force is nearly constant along the cir- cumference of the arch.

3. Buckling of Hinge-Ended Arch Prepare

The primary structure system is shown in Figure 2, as the first degree statically indeterminate structure of a Pin-ended arch, with notations the same as Figure 1. Assume that the horizontal force at the hinge joint is the primary unknown, the release of a redundant restraint introduces a compatibility condition for displacement of the primary system. In the original structure system, the deflection/displacement at hinge joint is zero, therefore, the basic equation in the force method [16] can be expressed as

. (13)

where represents a coefficient of proportionality, which is equal to the displacement in direction at the hinge joint when the primary structure system were subjected to the unit force alone. And re- presents the displacement at the hinge joint, corresponding to, due to the external load, when the primary system is subjected to the load.

The primary structure system can be treated as a curved beam, if the flexural deformation is (in a certain con- dition) dominant. Therefore, the coefficient and the constant term can be obtained from

. (14)

where is the bending rigidity of the curved beam arch and is the infinitesimal element (differential) of the arch length. is the moment at any cross section of the primary system due to. is the axial force at any cross section of the primary system due to. is the moment at any cross section of the primary system due to the external load.

For the primary system, the vertical reaction force due to is zero, so and at cross section are

. (15)

and at cross section due to the external loads also can be obtained as

. (16)

and can be obtained from Equation (14) based on Equation (15) and Equation (16)

. (17)

. (18)

where

The primary unknown can be obtained from Equation (13), by using Equation (17) and Equation (18)

. (19)

From the vertical equilibrium of the original structure system, the vertical reaction force can be obtained as

. (20)

The constant circumferential force can be obtained by using the primary unknown and the vertical reaction forces

. (21)

substitute Equation (19) and Equation (20) into Equation (21), we have

. (22)

The differential equation for the deflection of the arch based on the relative radial displacement while lo- cal buckling occurring can be expressed as

. (23)

where is the moment at any point of the local buckling position while local in-plane buckling occurring, just as in the Euler compression bar. The compression force is approximately equal to and can be ap- proximately represented as [17] [18] . Equation (23) can then be expressed as

. (24)

The corresponding boundary conditions are

. (25)

The general solution of the ordinary differential Equation (24) is

. (26)

where and are constant coefficients.

From the BCs Equation (25), we have

. (27)

When the corresponding constant coefficients satisfy, the solution is the trivial solu- tion, which represents the state of no loading and no deflection. The instability condition is that the non-trivial constants exist, as the solution of Equation (27), namely,. That means that the corres- ponding matrix determinant of in Equation (27) is equal to 0, or

. (28)

We will have, namely,

. (29)

The approximate axial force can be expressed as

. (30)

By substituting Equation (30) into Equation (22), the n-th order critical load is obtained as

. (31)

The dimensionless critical load is defined as following

. (32)

By substituting Equation (31) into Equation (32), this will leads to the dimensionless critical load as

. (33)

where modified slenderness is given by.

4. The Critical Instability Load and Numerical Results

From Equation (33), we find that the modified slenderness and included angle of an arch play important roles in the buckling. [3] shows the variation of the first four order dimensionless buckling load for pin-ended arches subjected to concentrated load at the crown with the included angle when. It can be observed from Figure 3, the dimensionless critical load of circular arch subjected to concentrated load at crown decreases with an increase of the included angle.

Figure 4 depicts the variation of the first four order dimensionless buckling load for pin-ended arch with the loading angle when and. It can be seen from Figure 4, the dimensionless buckling load increases with loading angle increase from crown to arch feet.

Figure 5 shows the variation of the first order dimensionless buckling load for different included angles pin-ended arch subjected to concentrated load at the crown with the modified slenderness. It can be observed that the dimensionless critical load decreases with the increase of modified slenderness. Obviously, for given the radius and half-angle of the circular arches, dimensionless critical loads mainly depend on the characteristic parameter of cross section.

Example 1: A steel arch structure

Arch structures are widely used in the engineering practice, especially in a coal mine roadway support. In this paper, a steel arch structure of roadway support in a certain coal mine is discussed, half included angle of arch is, the radius of arch is, moment inertia is, Young’s modulus of elas- ticity is and Poisson ratio is.

In order to compare the analytic solutions with numerical results, eigenvalue buckling analysis of the finite element software ANSYS is used to predict the critical loads. Table 1 lists the first three order critical loads of eigenvalue buckling analysis and the first four order critical loads of theoretical analysis with different loading angles. Figure 6 shows that different order critical loads vary with different loading positions. It can be ob- served that, the second order critical load of theoretical analysis corresponds to the lowest critical load of eigen- value buckling analysis, and each order results agree very well, which verifies the reasonableness of theory analysis. Table 2 shows the relative error of critical loads of theoretical analysis. It also can be seen that the re- sults of theoretical analysis and eigenvalue analysis agree with each other very well.

When n = 1, From the boundary conditions, namely, the integral constants can be determined, and the radial displacement can be obtained

as, the corresponding buckling mode is shown in Figure 7(a). Similarly, when n = 2, the radial displacement is, and corresponding buckling mode is shown in Figure 7(b). When n = 3, the radi- al displacement is, and corresponding buckling mode is shown in Figure 7(c). When n = 4, the radial displacement is, and corresponding buckling mode is shown in Figure 7(d). The buckling modes of numerical results obtained by eigenvalue buckling analysis are shown in Figure 8. The lowest order buckling mode corresponds to anitsymmetric buckling form with two semi waves, and the third order buckling mode corresponds to symmetric buckling form with three semi waves, and so on. For the third-order symmetric buckling mode, there are two deformations: (a) vault sink and two sides crush to rock; (b) vault uplift and two sides crush to the roadway. Both possibly occur in practice. It also can be seen that the lowest-order buckling mode of eigenvalue buckling analysis corresponds to the second order buckling mode.

Traditionally, two buckling analysis techniques are available in ANSYS for predicting the buckling load and buckling mode shape of a structure, nonlinear buckling analysis and eigenvalue (or linear) buckling analysis. The eigenvalue buckling analysis predicts the theoretical buckling strength of an ideal linear elastic structure. This method corresponds to the textbook approach of elastic buckling analysis. The nonlinear buckling analysis employs a nonlinear static analysis with gradually increasing loads to seek the load level at which the structure becomes unstable. If not inflicting any initial defects on the ideal perfect structure, geometry nonlinear analysis couldn’t predict the critical load accurately. Generally in engineering, the method of imposing certain initial de-

fects is adopted to approximate the actual critical load of structures, but this method will change the geometrical model. In addition to the above two numerical methods, we put forward a transient analysis method for buckling analysis [19] , and the dynamic response of the loading process and inertial iterative process could be regarded as a kind of tiny disturbance.

Table 3 shows second order buckling critical load of several different analysis methods. Here, we impose 5‰ maximum displacement of eigenvalue buckling analysis as initial imperfection in geometrical nonlinear analysis. Figure 9 shows critical loads by different methods vary with different loading positions.

5. Conclusions

The following conclusions can be drawn:

1) This paper gives a theoretical analysis of the local instability of circular arches subjected to a concentrated load.

2) The virtual work method is used to derive the equilibrium equation for pin-ended circular arches, and it is shown that the axial force is nearly constant along the circumference of the circular arches subjected to a concentrated load.

3) Based on force methods, the primary eigenfunction equation is derived and solved, and the approximate analytical solutions of critical instability loads are obtained. The buckling load increases with loading angle increasing from crown to arch feet and the critical load decreases with increasing of modified slenderness.

4) For a practical steel arch structure of the roadway support in a certain coal mine in the south of China, the theory predictions results agree very well with the eigenvalue buckling analysis results of ANSYS.

5) The analytical solutions and numerical results prove that the method and approximate theoretical analysis formula in this paper are practical and feasible, and can be used directly in engineering practices in the eval- uation of the critical loads of arches.

References