Engineering
Vol.6 No.8(2014), Article
ID:47933,10
pages
DOI:10.4236/eng.2014.68048
Traffic Dynamics and Congested Phases Derived from an Extended Optimal-Velocity Model
Makoto Watanabe
Faculty of Humanity and Environment, Hosei University, Tokyo, Japan
Email: makoto@hosei.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 May 2014; revised 15 May 2014; accepted 25 June 2014
ABSTRACT
Dynamics is studied for one-dimensional single-lane traffic flow by means of an extended optimal-velocity model with continuously varied bottleneck strength for nonlinear roads. Two phases exist in this model such as free flow and wide moving jam states in the systems having relatively small values of the bottleneck strength parameter. In addition to the two phases, locally congested phase appears as the strength becomes prominent. Jam formation occurs with the similar mechanism to the boomerang effect as well as the pinch one in it. Wide scattering of the flow-density relation in fundamental diagram is found in the congested phase.
Keywords:Optimal-Velocity Model, Phase Transition, Synchronized Flow, Jam Formation Mechanism, Fundamental Diagram

1. Introduction
Study of phase transition behavior in vehicular dynamics is one of the interesting themes in traffic systems. Kerner has proposed the three-phase traffic theory in describing the nature of the dynamics [1] -[4] . The theory requires the existence of the three states such as free flow (FF), synchronized flow (SF), and wide moving jam (WMJ) phases. The WMJ phase has a moving jam running through various states including bottlenecks. On the other hand, the SF phase is for all congested states which are not belonging to the WMJ state. Jam formation mechanism in the theory is as follows. First the transition from FF to SF occurs and later the other transition from SF to WMJ occurs in highways: moving jams emerge through FF ® SF ® WMJ states [1] -[4] . Jams are not formed directly in the FF state. The “general pattern” has been well known as a typical type of jam formation mechanism. When SF is formed at a bottleneck, self-compression occurs into a high density state. Then local perturbation grows and forms narrow jams [1] . This self-compression has been called as the pinch effect. Narrow jams grow to a wide jam by merging mechanism with other jams. Here the narrow moving jams are classified as a state of the SF phase [2] [3] . A characteristic feature of the SF state is to have wide scattering behavior of flow ![]() and density
and density ![]() on a two dimensional region of the fundamental diagram [1] -[6] . This behavior has been imaginarily depicted as an oblique and round triangle with tapering both sides on the diagram (see, for instance, Figure 4 in [1] and Figure 4.4 in [2] ). For the FF state, it gives a simple curve on the diagram [1] -[4] .
on a two dimensional region of the fundamental diagram [1] -[6] . This behavior has been imaginarily depicted as an oblique and round triangle with tapering both sides on the diagram (see, for instance, Figure 4 in [1] and Figure 4.4 in [2] ). For the FF state, it gives a simple curve on the diagram [1] -[4] .
Recently, critical discussions to the theory have been expressed by Schönhof and Helbing [7] [8] . Kerner has divided the SF state into three types such as stationary and homogeneous states, homogeneous-in-speed states, and non-stationary and non-homogeneous states [5] [8] . Schönhof et al. have stated that such multifariousness undermines the concept of the SF state as a single phase [8] . The general pattern with pinch effect of vehicles, as a central concept of jam-formation mechanism in the theory, was pointed out to be not general: it is a specific state appearing on a section between onand off-ramps. This indicates that it is a result of a particular freeway design [7] [8] . Although the theory has not recognized the occurrence of the transition from FF to WMJ phases, they have found that the transition actually occurs. It is attributed to the heterogeneity of traffic flow given by cars and trucks having different speeds: the boomerang effect has given trigger of WMJ [7] [8] . If two kinds of vehicles are considered such as cars and trucks, empirically observed flow-density relation with wide scattering in fundamental diagrams is reproduced [7] -[9] . The classification of congestion patterns in the theory has been claimed to be not well defined. The theory has used 13 different criteria in explaining the traffic states as three phases [8] . In order to explain the congestion states, Schönhof et al. classified them into several patterns such as moving localized cluster (MLC), oscillating congested traffic (OCT), pinned localized cluster (PLC), stop-andgo waves (SGW), and homogeneous congested traffic (HCT) [7] .
As shown in the above place, Schönhof and Helbing questioned the three-phase traffic theory [7] . One of reasons of the indication may arise from the complexity of the SF phase. From their discussion [7] [8] , we feel the following necessity. First we have to describe an image of the SF phase more simply and distinguish the SF phase from the WMJ phase. This may necessarily be investigated with the fundamental diagram which plays a role of phase map. Second it is important to clarify the jam formation mechanism and examine the relation to the congestion patterns. In this paper the simulation results will be reported for a microscopic model with the continuous bottleneck effect. The locally congested phase, which seems to be identical with the SF phase by Kerner, will be clearly recognized and separated from the WMJ phase in the fundamental diagram. Jam formation mechanism will be clarified later.
2. Model
There have been various models proposed in simulating traffic dynamics in highways. The optimal-velocity (OV) model, proposed by Bando et al. [10] -[12] , has been known as a car-following type model in microscopic scale. This model has been known to reproduce phase transition between freely flowing state and jamming one. In this paper the OV model is basically adopted.
We find complex geometry in actual highways, for instance, such as horizontal curves, uphill gradients, downhill slopes, ramps, and other structures. Drivers should incessantly adjust their speed in responding to road shape. There has been negative correlation between actual operating speed of vehicles and road curvature at each measuring point on highways [13] . Sentou et al. have proposed a method to calculate the safe speed on curves in a test track. The speed profile has shown to vary with road curvature [14] . Thus the effect of continuously varied road geometry is important to be considered.
We introduce the effect of bottleneck strength into the OV model. First, in the original OV model, the equation of motion for each vehicle is given as [10] -[12]
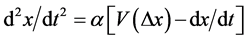 , (1)
, (1)
where 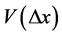 is the objective velocity which is a function of headway
is the objective velocity which is a function of headway . As a realistic dynamical model, the following function has been proposed [10] -[12] :
. As a realistic dynamical model, the following function has been proposed [10] -[12] :
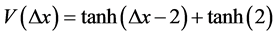 . (2)
. (2)
Recently it was applied to the system with the effects of gravitational force on road or highway tollgates [15] [16] .
Let us imagine vehicle movements, for instance, on horizontally curved roads. We have introduced the function  into
into 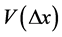 as
as
 , (3)
, (3)
where ![]() is the position of a vehicle on a road. The
is the position of a vehicle on a road. The  is defined as a function of road curvature. Here we consider the road whose curvature continuously changes. In the case of road shape expressed by
is defined as a function of road curvature. Here we consider the road whose curvature continuously changes. In the case of road shape expressed by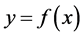 , the curvature
, the curvature 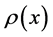 at position
at position ![]() is defined as
is defined as
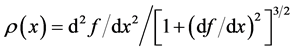 . (4)
. (4)
when road shape is continuously periodic like a sine curve, the road curvature is expressed by
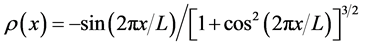 (5)
(5)
where ![]() is the road length of the system. Using Equation (5), we have introduced the extended OV function as [17] [18]
is the road length of the system. Using Equation (5), we have introduced the extended OV function as [17] [18]
 (6)
(6)
where 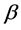 is a bottleneck strength parameter as
is a bottleneck strength parameter as 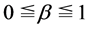 and
and  is the maximum value of
is the maximum value of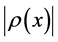 . The absolute value is taken because the objective velocity is independent of curve direction in the case of the traffic dynamics on roads. The function
. The absolute value is taken because the objective velocity is independent of curve direction in the case of the traffic dynamics on roads. The function 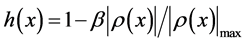 shows a double-valley shape: it has the minimum value at positions
shows a double-valley shape: it has the minimum value at positions 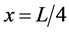 and
and 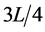 and the maximum value at
and the maximum value at 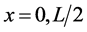 and
and ![]() [17] . This model may be applicable to the systems having vertical slopes whose gradient continuously varies as a function of road position: Equations (5) and (6) may be regarded as a road with a double-mountain shape vertically changed.
[17] . This model may be applicable to the systems having vertical slopes whose gradient continuously varies as a function of road position: Equations (5) and (6) may be regarded as a road with a double-mountain shape vertically changed.
3. Fundamental Diagram
We have simulated the time development of positions and velocities of vehicles with Equation (1). In this paper the function 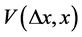 as Equation (6) with Equation (5) was used. The sensitivity constant
as Equation (6) with Equation (5) was used. The sensitivity constant ![]() in Equation (1) was set as
in Equation (1) was set as 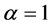 through all simulations. The road length was defined as
through all simulations. The road length was defined as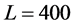 . The periodic boundary condition (PBC) was adopted in the system. The density
. The periodic boundary condition (PBC) was adopted in the system. The density ![]() of the system is defined as
of the system is defined as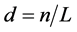 , where n is the number of vehicles constructed in the system. We simulated vehicular movement in the system until
, where n is the number of vehicles constructed in the system. We simulated vehicular movement in the system until  for a fixed density and for a fixed parameter
for a fixed density and for a fixed parameter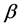 . The densities for each run were varied from
. The densities for each run were varied from  to
to 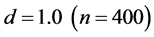 having the density interval
having the density interval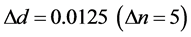 . The value of the parameter β was changed from
. The value of the parameter β was changed from 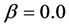 to
to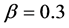 .
.
Figure 1 shows the fundamental diagram for the present model. Abscissa is for density ![]() and ordinate for flow
and ordinate for flow ![]() which has been obtained from the product of the average velocity v and d of the system. Open triangles are for the system with
which has been obtained from the product of the average velocity v and d of the system. Open triangles are for the system with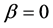 , open circles for
, open circles for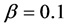 , filled triangles for
, filled triangles for , and filled circles for
, and filled circles for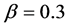 . The average velocities were obtained from the time range between
. The average velocities were obtained from the time range between 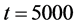 and
and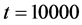 . The data for
. The data for 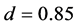 with
with 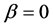 and for
and for  with
with 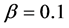 were omitted from it because they involved transition process during the time period.
were omitted from it because they involved transition process during the time period.
As shown in Figure 1, flow q for  increases with increasing d in the initial region along the theoretical curve given as
increases with increasing d in the initial region along the theoretical curve given as  in Equation (3). It decreases abruptly at around
in Equation (3). It decreases abruptly at around 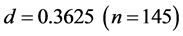 and decreases linearly with
and decreases linearly with ![]() in the region until
in the region until . It varies along the line again for
. It varies along the line again for 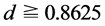
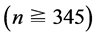 . For
. For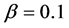 , it increases with increasing d in the initial region along the theoretical curve given as
, it increases with increasing d in the initial region along the theoretical curve given as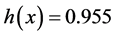 . (This is the average value of
. (This is the average value of ). It drops down at
). It drops down at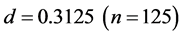 , and after that, it decreases linearly with increasing d until
, and after that, it decreases linearly with increasing d until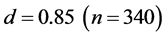 .
.
The different behavior has been found for larger values of the parameter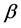 . Flow q for
. Flow q for 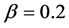 increases with increasing
increases with increasing ![]() along the theoretical curve for
along the theoretical curve for 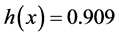 in the initial region. It becomes constant for
in the initial region. It becomes constant for
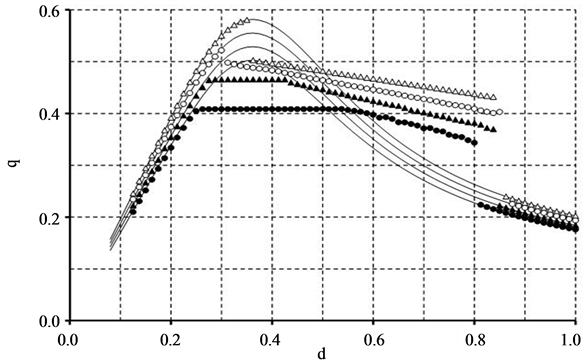
Figure 1. Fundamental diagram as the relation between flow 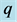 and density
and density 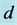 of the system. Open triangles are for the system with
of the system. Open triangles are for the system with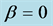 , open circles for
, open circles for , filled triangles for
, filled triangles for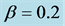 , and filled circles for
, and filled circles for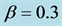 .
.
the density region between  and
and . It decreases linearly as density increases for the region from
. It decreases linearly as density increases for the region from 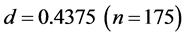 to
to . For the case of
. For the case of , flow q increases with
, flow q increases with ![]() in the initial region and becomes constant between
in the initial region and becomes constant between 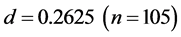 and
and 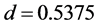
 . At
. At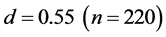 , it begins to deviate from the horizontal relation and after that it decreases linearly with increasing
, it begins to deviate from the horizontal relation and after that it decreases linearly with increasing ![]() until
until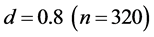 . It varies along the theoretical curve with
. It varies along the theoretical curve with 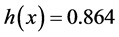 again for
again for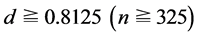 .
.
In summary of this section, we observed the existence of two states in the fundamental diagram of the systems for relatively small values as 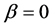 and
and . One of them is for the simply increasing relation from the origin in a lower density region of the diagram. This corresponds to the free flow state. Another state is for the oblique linear relation located on higher density region than it. As the value of the parameter
. One of them is for the simply increasing relation from the origin in a lower density region of the diagram. This corresponds to the free flow state. Another state is for the oblique linear relation located on higher density region than it. As the value of the parameter 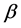 increases, horizontal linear relation is added into the two relations: three states occur for the systems with
increases, horizontal linear relation is added into the two relations: three states occur for the systems with 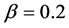 and
and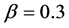 . We will examine the origin of the slope change between the horizontal and the oblique linear relations later.
. We will examine the origin of the slope change between the horizontal and the oblique linear relations later.
4. Congestion Behavior
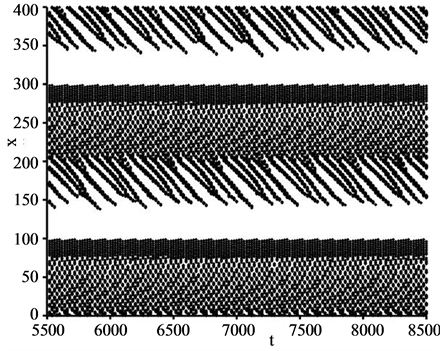
In order to know dynamic features of vehicles, we have obtained the time development of positions of all vehicles constructed in the system. First we examined the case of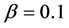 . Figure 2(a) shows the result for the density
. Figure 2(a) shows the result for the density  with
with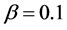 . This density corresponds to the just dropped point for open circles in Figure 1. Abscissa is for time t and ordinate for positions
. This density corresponds to the just dropped point for open circles in Figure 1. Abscissa is for time t and ordinate for positions ![]() of vehicles. The time period depicted in the figure is between
of vehicles. The time period depicted in the figure is between 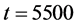 and
and . The upper direction of ordinate corresponds to the downstream site of the system and the lower direction to the upstream one. The WMJ pattern appears in the figure. This pattern shows the jam propagation to the upstream direction with time.
. The upper direction of ordinate corresponds to the downstream site of the system and the lower direction to the upstream one. The WMJ pattern appears in the figure. This pattern shows the jam propagation to the upstream direction with time.
The other patterns have been found for different values of 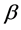 in the present model. Figure 2(b) shows the time development for
in the present model. Figure 2(b) shows the time development for 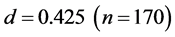 with
with . This density is located at the right end of the constant flow region for
. This density is located at the right end of the constant flow region for 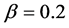 (filled triangles) in Figure 1. Narrow jams with finite lifetime are arranged regularly in it. The downstream fronts of the jams are located at around
(filled triangles) in Figure 1. Narrow jams with finite lifetime are arranged regularly in it. The downstream fronts of the jams are located at around 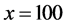 or
or 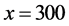 which almost coincide with the positions having the maximum bottleneck strength, i.e. having the minimum value of the function
which almost coincide with the positions having the maximum bottleneck strength, i.e. having the minimum value of the function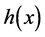 .
.
We have examined the development at  with the same value of
with the same value of . This density is located at the left end of the negative-sloped linear relation for filled triangles in Figure 1. The result is shown in Figure 2(c). In the figure moving jams spanning the system appear in the array of narrow jams. Thus the turning behavior at around
. This density is located at the left end of the negative-sloped linear relation for filled triangles in Figure 1. The result is shown in Figure 2(c). In the figure moving jams spanning the system appear in the array of narrow jams. Thus the turning behavior at around 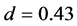 for filled triangles in Figure 1 is caused by the transition from the locally congested state to the widely jammed one penetrating through the system.
for filled triangles in Figure 1 is caused by the transition from the locally congested state to the widely jammed one penetrating through the system.
 (a)
(a)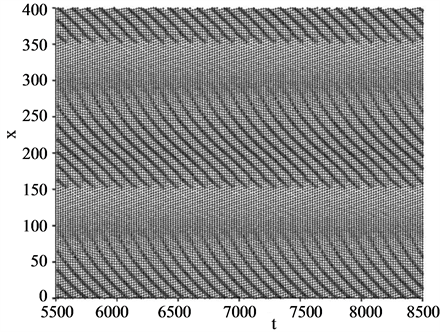 (b)
(b)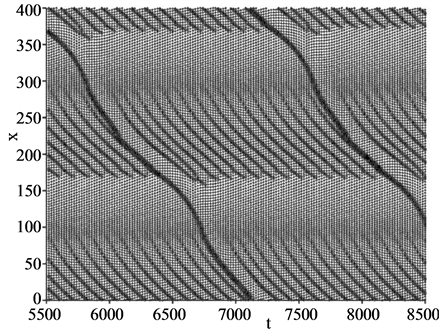 (c)
(c)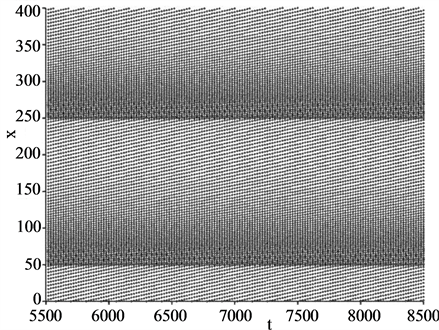 (d)
(d) (e)
(e)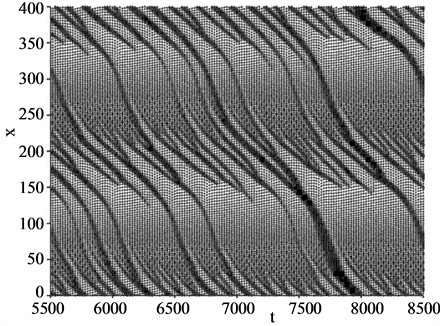 (f)
(f)
Figure 2. Time developments of positions of all vehicles in the system. (a) for  and
and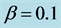 ; (b) for
; (b) for  and
and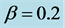 ; (c) for
; (c) for  and
and ; (d) for
; (d) for 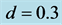 and
and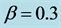 ; (e) for
; (e) for 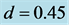 and
and ; and (f) for
; and (f) for  and
and . Time range is between
. Time range is between  and
and  for these figures.
for these figures.
Let us examine the case for . Figure 2(d) shows the time development for
. Figure 2(d) shows the time development for 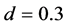 and
and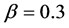 . This is within the constant region for filled circles in Figure 1. We find two horizontal jams which are immovable at fixed positions. These two jams have been formed independently each other in the system. The jam pattern changes with increasing
. This is within the constant region for filled circles in Figure 1. We find two horizontal jams which are immovable at fixed positions. These two jams have been formed independently each other in the system. The jam pattern changes with increasing ![]() for the same coefficient
for the same coefficient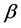 . Figure 2(e) shows the case for
. Figure 2(e) shows the case for 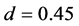 which is within the constant region for the filled circles in Figure 1. The combination of different kinds of jams is found in it. Narrow jams locally occur on upstream front of horizontally fixed jams. Another pattern has been found as density increases for the same parameter
which is within the constant region for the filled circles in Figure 1. The combination of different kinds of jams is found in it. Narrow jams locally occur on upstream front of horizontally fixed jams. Another pattern has been found as density increases for the same parameter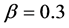 . Figure 2(f) shows the time development at
. Figure 2(f) shows the time development at 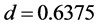
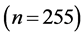 . This is in the negative-sloped region for filled circles in Figure 1. We find frequent WMJs running through the system from top to bottom of the figure. Time intervals between these jams are different one after another.
. This is in the negative-sloped region for filled circles in Figure 1. We find frequent WMJs running through the system from top to bottom of the figure. Time intervals between these jams are different one after another.
From Figure 1 and Figure 2, we saw the following results. Locally congested phase, which is free from wide jams running through whole range of the system, gives the horizontal linear relation in the fundamental diagram. On the other hand, wide moving jam phase gives the oblique linear relation in it.
5. Jam Formation Mechanism
As shown in Figures 2(a)-(f) there have been various congestion patterns in the present model. In this section we examine jam formation process in detail. In clarifying the jamming mechanism, it is effective to refer to the three dimensional diagram of time development of local density of the system [18] . Figure 3(a) shows the variation of the density as a function of road position ![]() of the system for
of the system for 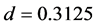 and
and . These values have been the same as Figure 2(a) in which moving jams have occurred. In this figure two bumps are found to propagate downstream (to the right side of abscissa) in the initial time region. The bumps change their propagating direction suddenly at a middle time range in the figure and proceeds upstream with time. This is the same type behavior as the boomerang effect [7] [8] . The direction change occurs near the road positions
. These values have been the same as Figure 2(a) in which moving jams have occurred. In this figure two bumps are found to propagate downstream (to the right side of abscissa) in the initial time region. The bumps change their propagating direction suddenly at a middle time range in the figure and proceeds upstream with time. This is the same type behavior as the boomerang effect [7] [8] . The direction change occurs near the road positions 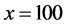 and
and  in the system. They correspond to the positions with the maximum bottleneck strength in the system. Thus the boomerang effect (or the similar mechanism to it) is caused by the bottleneck effect varied continuously in the system. The direct formation of moving jams from FF state without the pinch effect is possible for the present system.
in the system. They correspond to the positions with the maximum bottleneck strength in the system. Thus the boomerang effect (or the similar mechanism to it) is caused by the bottleneck effect varied continuously in the system. The direct formation of moving jams from FF state without the pinch effect is possible for the present system.
We have recognized the formation of regularly arranged narrow jams as shown in Figure 2(b). This pattern occurs with different mechanism from Figure 3(a). Figure 3(b) shows the time development for 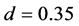 and
and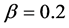 . These values have given the same type jams as Figure 2(b). Curved slopes appear in the regions for
. These values have given the same type jams as Figure 2(b). Curved slopes appear in the regions for  and for
and for . The density increases with decreasing x within each region: the density for upstream site is higher than that for downstream one within each region. Narrow jams begin to appear at around the positions
. The density increases with decreasing x within each region: the density for upstream site is higher than that for downstream one within each region. Narrow jams begin to appear at around the positions  and
and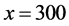 . Local density increment, i.e. self-compression having the bottleneck effect at around these positions, becomes trigger for the marrow jam formation.
. Local density increment, i.e. self-compression having the bottleneck effect at around these positions, becomes trigger for the marrow jam formation.
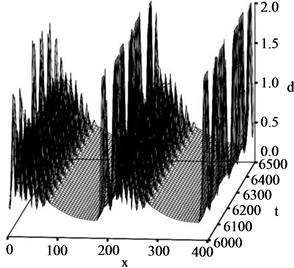
We have observed another pattern concerning narrow jam formation. Figure 3(c) shows the time development of local density for 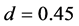 and
and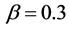 . These values are the same as Figure 2(e). There are smoothly sloped regions for
. These values are the same as Figure 2(e). There are smoothly sloped regions for 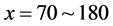 and for
and for . On the just upstream front of the regions, we find density fluctuating areas for
. On the just upstream front of the regions, we find density fluctuating areas for 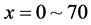 and for
and for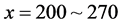 . This is given by the self-compression of vehicles. These regions are located just at downstream fronts of the narrow jams occurred in the system near
. This is given by the self-compression of vehicles. These regions are located just at downstream fronts of the narrow jams occurred in the system near 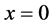 and
and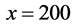 .
.
Kerner has suggested that the general pattern is the important concept as the jam formation mechanism on highways. The pattern is as follows [1] . Simultaneously with SF appearance in roads, self-compression occurs
 (a)
(a)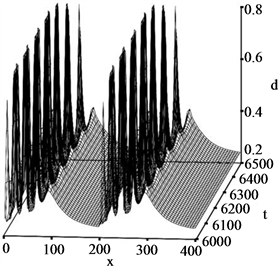 (b)
(b)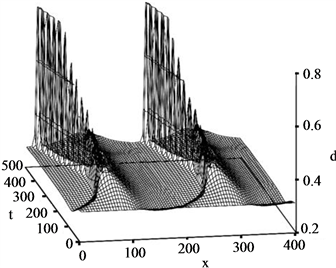 (c)
(c)
Figure 3. Three dimensional projections of time developments of local density ![]() as a function of position
as a function of position![]() . (a) for
. (a) for  and
and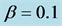 , (b) for
, (b) for 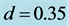 with
with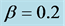 , and (c) for
, and (c) for 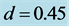 with
with .
.
into a high density state. Then local perturbation grows and it forms narrow jams. The self-compressed state is called as the pinch effect. The wide jams are formed by merging and dissolution of the jams. Figure 3(c) shows the occurrence of the pinch effect accompanying self-compression with the local perturbation.
We see the process of wide jam formation from the pinch region. Figure 4(a) shows the time development of vehicular positions for 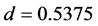 with
with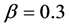 . This density has been located at the right end of the constant flow region for filled circles in Figure 1. Vehicles with low velocity as
. This density has been located at the right end of the constant flow region for filled circles in Figure 1. Vehicles with low velocity as 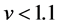 are depicted in it: vehicles with
are depicted in it: vehicles with 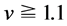 are omitted from the figure. We find three areas exist in it. One of them is the black belts located on
are omitted from the figure. We find three areas exist in it. One of them is the black belts located on 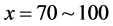 and on
and on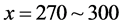 . They correspond to smooth slopes in Figure 3(c). The other is stripe belts located on
. They correspond to smooth slopes in Figure 3(c). The other is stripe belts located on 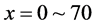 and on
and on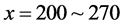 . They are for self-compressed perturbing areas in Figure 3(c). The last is for narrow jams located on the regions
. They are for self-compressed perturbing areas in Figure 3(c). The last is for narrow jams located on the regions 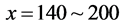 and on
and on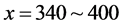 . We do not have wide jams through the system from top to bottom in the figure. This has been the common feature within the constant flow region of the filled circles with
. We do not have wide jams through the system from top to bottom in the figure. This has been the common feature within the constant flow region of the filled circles with 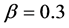 in Figure 1.
in Figure 1.
Figure 4(b) shows the vehicle positions with the velocity 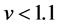 for
for 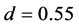 and
and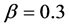 . This is the onset density to deviate from the horizontal relation and is located at the left end of the oblique linear relation for filled circles in Figure 1. We can find not only narrow jams but also the wide jam spanning the system from top to bottom of this figure. The jam occurred on the position
. This is the onset density to deviate from the horizontal relation and is located at the left end of the oblique linear relation for filled circles in Figure 1. We can find not only narrow jams but also the wide jam spanning the system from top to bottom of this figure. The jam occurred on the position 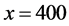 at around
at around 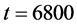 proceeds in the system and goes over the bottleneck positions
proceeds in the system and goes over the bottleneck positions  and
and . It combines surrounding jams. This is the same process of wide jam formation as Kerner’s analysis as shown in Figure 6 and its caption in [1] .
. It combines surrounding jams. This is the same process of wide jam formation as Kerner’s analysis as shown in Figure 6 and its caption in [1] .
6. Wide Scattering of Flow-Density Relation
Wide scattering of flow-density relation with time has been a characteristic feature of the SF state [1] -[5] . In this section we examine whether or not the scattering behavior occurs in the present model. First time development of local flow-density relation has been analyzed for the system with 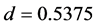 for
for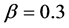 . They are the same values as Figure 4(a). Here we define the local density as
. They are the same values as Figure 4(a). Here we define the local density as 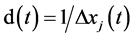 and the local flow as
and the local flow as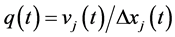 , where
, where 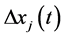 is the headway of vehicle j which is located just before the road position
is the headway of vehicle j which is located just before the road position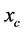 . The result is shown in Figure 5(a). This was obtained for
. The result is shown in Figure 5(a). This was obtained for 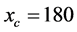 from the time range between
from the time range between 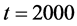 and
and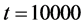 . Small dots in it were obtained with time interval
. Small dots in it were obtained with time interval . A line drown from the origin is for the theoretical flow as
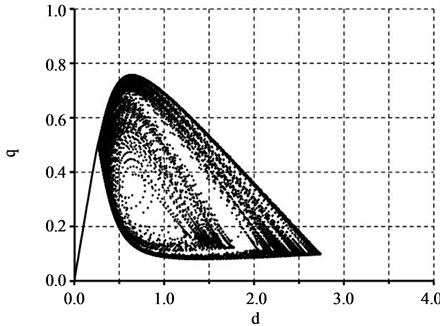
. A line drown from the origin is for the theoretical flow as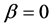 , which is depicted for location guidance in it. The q-d relation scatters widely in the two dimensional region of the diagram. The dots describe a round triangle shape with pointed end. Kerner has imaginarily illustrated the area of the SF state in the fundamental diagram [1] [2] . The area has been oblique and round triangle with tapering both sides (see, for instance, Figure 4 in [1] and Figure 4.4 in [2] ). The shape of the dots observed in Figure 5(a) is somewhat similar to the Kerner’s illustration described in the references.
, which is depicted for location guidance in it. The q-d relation scatters widely in the two dimensional region of the diagram. The dots describe a round triangle shape with pointed end. Kerner has imaginarily illustrated the area of the SF state in the fundamental diagram [1] [2] . The area has been oblique and round triangle with tapering both sides (see, for instance, Figure 4 in [1] and Figure 4.4 in [2] ). The shape of the dots observed in Figure 5(a) is somewhat similar to the Kerner’s illustration described in the references.
 (a)
(a)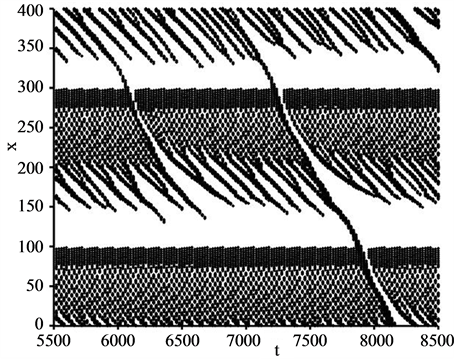 (b)
(b)
Figure 4. Time developments of positions ![]() of vehicles in the system. The vehicles whose velocity is less than 1.1 are depicted. (a) for
of vehicles in the system. The vehicles whose velocity is less than 1.1 are depicted. (a) for  as
as 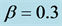 and (b) for
and (b) for 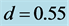 as
as . Time range is between
. Time range is between  and
and  for these figures.
for these figures.
In actual measurement, the q-d relation on a fixed position on highways was evaluated as one minute interval [5] [6] . We should take account of the interval effect. We have averaged the local flow and the local density during a time period tp. Figure 5(b) shows the result for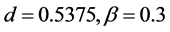 , and
, and 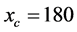 which are the same values as Figure 5(a). The time period
which are the same values as Figure 5(a). The time period  for the averaging has been chosen to be
for the averaging has been chosen to be  which almost corresponds to one minute in realistic highway. (The measured flow has been found to scatter at around the flow rate 1500 vehicles/h (i.e. 25 vehicles/min) as shown in Figure 2 in [5] . On the other hand, the tapering point on the left side in the q-d relation in Figure 5(a) is about
which almost corresponds to one minute in realistic highway. (The measured flow has been found to scatter at around the flow rate 1500 vehicles/h (i.e. 25 vehicles/min) as shown in Figure 2 in [5] . On the other hand, the tapering point on the left side in the q-d relation in Figure 5(a) is about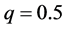 ). Figure 5(b) includes 160 points as circles obtained from the simulation data between
). Figure 5(b) includes 160 points as circles obtained from the simulation data between 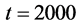 and
and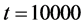 . Successive points in time are connected with lines in this figure. As location guidance, the same line as Figure 5(a) is drown from the origin. Circles in Figure 5(b) scatter widely on the two dimensional region from place to place in the fundamental diagram. This is almost the same behavior as empirical observation in highways [5] . Thus the wide scattering of the flow-density relation occurs for the present model of a single-lane traffic.
. Successive points in time are connected with lines in this figure. As location guidance, the same line as Figure 5(a) is drown from the origin. Circles in Figure 5(b) scatter widely on the two dimensional region from place to place in the fundamental diagram. This is almost the same behavior as empirical observation in highways [5] . Thus the wide scattering of the flow-density relation occurs for the present model of a single-lane traffic.
7. Discussion
In this paper we have found various patterns of congested states as shown in Figures 2(a)-(f). Schönhof and Helbing have classified the states into five patterns such as MLC, OCT, PLC, SGW, and HCT [7] [8] . We discuss whether or not the classification is valid for the present model. The pattern MLC is a single moving jam with a localized width. The boomerang effect has been easily found in the MLC formation [7] . In this paper we found isolated and limited jams in width as shown in Figure 2(a). The same mechanism as the effect has been shown in Figure 3(a). Thus these figures give the MLC pattern. As for the OCT pattern, it accompanies regular oscillations of speed of vehicles. Narrow jams have been arranged with regular intervals as shown in Figure 11 in [7] . The OCT has been triggered by a perturbation [7] . Figure 2(b) in the present paper shows the same shape as it. As shown in Figure 3(b) for the present system, self-compression of vehicles has yielded the jam arrangement. This is consistent with the statement concerning the OCT pattern in [7] . Thus Figure 2(b) indicates the OCT. In the case of the PLC pattern, it is characterized by a local density increment at fixed positions. This has normally occurred at bottlenecks such as on-ramps or gradients. It has been stated that this pattern develops to other extended congestion states including the pinch effect [7] . Figure 9(a) in [7] has shown almost similar pattern to Figure 2(d). This indicates that the PLC occurs in this model. The SGW consists of a sequence of moving jams. The temporal and spatial intervals between two successive jams have been considerably changed. The PLC or perturbation sometimes becomes a trigger of the SGW [7] Figure 2(f) has shown the sequence of moving jams through the system. It gives almost the same jams as Figure 12 in [7] . Thus the SGW exists in the model. As for the HCT, it may be somewhat particular case. This pattern, for instance, has occurred after
 (a)
(a)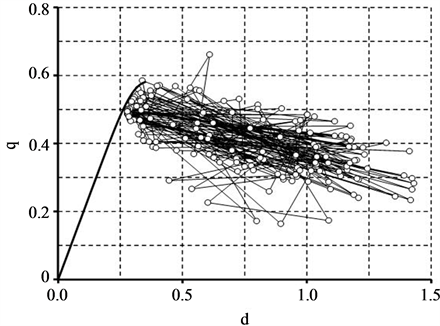 (b)
(b)
Figure 5. (a) Variation of local flow-densityrelation at the position 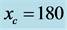 for the system with
for the system with  and
and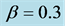 . Abscissa is for density
. Abscissa is for density ![]() and ordinate for flow
and ordinate for flow ![]() at the position. Small dots are depicted with time interval
at the position. Small dots are depicted with time interval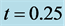 . (b) Variation of time-averaged local flow-density relation at the same position
. (b) Variation of time-averaged local flow-density relation at the same position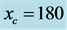 . The values of
. The values of ![]() and
and ![]() are
are  and
and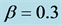 . Time average is taken over
. Time average is taken over 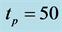 for both of density and flow. Succeeded points in time are connected with lines.
for both of density and flow. Succeeded points in time are connected with lines.
serious accidents with lane closing [7] . It happens when highways suddenly have extremely strong bottlenecks or so. This pattern HCT has not been observed clearly in the present system.
8. Concluding Remarks
Vehicular dynamics has been simulated for one-dimensional single-lane traffic flow by means of the optimal-velocity model with continuously varied bottleneck strength for nonlinear lanes. The strength is adjusted with the value of the parameter 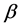 in the optimal-velocity function for the system. The model succeeds to reproduce empirically observed congestion patterns such as moving localized cluster, oscillating congested traffic, pinned localized cluster, and stop-and-go waves.
in the optimal-velocity function for the system. The model succeeds to reproduce empirically observed congestion patterns such as moving localized cluster, oscillating congested traffic, pinned localized cluster, and stop-and-go waves.
Two phases exist in the systems for relatively small values of the parameter as 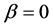 or
or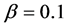 . They are free flow and wide moving jam phases. The wide moving jam phase is characterized by the oblique linear relation in the flow-density relation as the fundamental diagram. The similar mechanism to the boomerang effect is observed in the jam formation process. Three phases appear in the systems for lager values of the parameter as
. They are free flow and wide moving jam phases. The wide moving jam phase is characterized by the oblique linear relation in the flow-density relation as the fundamental diagram. The similar mechanism to the boomerang effect is observed in the jam formation process. Three phases appear in the systems for lager values of the parameter as 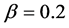 or
or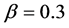 . In addition to the free flow and the wide moving jam phases, locally congested phase being free from wide moving jams running through the system appears for the values of
. In addition to the free flow and the wide moving jam phases, locally congested phase being free from wide moving jams running through the system appears for the values of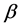 . This phase, corresponding with the synchronized flow state in the three-phase traffic theory, accompanies the horizontal linear relation in the diagram. The pinch effect as the general pattern in the three-phase traffic theory is observed in the system as the bottleneck strength becomes large.
. This phase, corresponding with the synchronized flow state in the three-phase traffic theory, accompanies the horizontal linear relation in the diagram. The pinch effect as the general pattern in the three-phase traffic theory is observed in the system as the bottleneck strength becomes large.
Locally defined flow-density relation without time average describes a round triangle shape with tapering vertices. This is almost similar to the shape schematically illustrated by Kerner as the area of the SF state in the fundamental diagram. The present model succeeds to reproduce the widely scattering behavior in the time averaged flow-density relation. This is identical with the fundamental diagrams actually observed in highways.
References
- Kerner, B.S. (1999) The Physics of Traffic. Physics World, 12, 25-30.
- Kerner, B.S. (2004) The Physics of Traffic. Springer, Heidelberg. http://dx.doi.org/10.1007/978-3-540-40986-1
- Kerner, B.S. (2004) Three-Phase Traffic Theory and Highway Capacity. Physica A, 333, 379-440. http://dx.doi.org/10.1016/j.physa.2003.10.017
- Kerner, B.S. (2009) Introduction to Modern Traffic Flow Theory and Control. Springer, Heidelberg. http://dx.doi.org/10.1007/978-3-642-02605-8
- Kerner, B.S. and Rehborn, H. (1996) Experimental Properties of Complexity in Traffic Flow. Physical Review E, 53, R4275-R4278. http://dx.doi.org/10.1103/PhysRevE.53.R4275
- Kerner, B.S. (1998) Experimental Features of Self-Organization in Traffic Flow. Physical Review Letters, 81, 3797-3800. http://dx.doi.org/10.1103/PhysRevLett.81.3797
- Schönhof, M. and Helbing, D. (2007) Empirical Features of Congested Traffic States and Their Implications for Traffic Modeling. Transportation Science, 41, 135-166. http://dx.doi.org/10.1287/trsc.1070.0192
- Schönhof, M. and Helbing, D. (2009) Criticism of Three-Phase Traffic Theory. Transportation Research Part B, 43, 784-797. http://dx.doi.org/10.1016/j.trb.2009.02.004
- Treiber, M. and Helbing, D. (1999) Macroscopic Simulation of Widely Scattered Synchronized Traffic States. Journal of Physics A, 32, L17-L23. http://dx.doi.org/10.1088/0305-4470/32/1/003
- Bando, M., Hasebe, K., Nakayama, A., Shibata, A. and Sugiyama, Y. (1994) Structure Stability of Congestion in Traffic Dynamics. Japanese Journal of Industrial and Applied Mathematics, 11, 203-223. http://dx.doi.org/10.1007/BF03167222
- Bando, M., Hasebe, K., Nakanishi, K., Nakayama, A., Shibata, A. and Sugiyama, Y. (1995) Phenomenological Study of Dynamical Model of Traffic Flow. Journal of Physics I France, 5, 1389-1399. http://dx.doi.org/10.1051/jp1:1995206
- Bando, M., Hasebe, K., Nakayama, A., Shibata, A. and Sugiyama, Y. (1995) Dynamical Model of Traffic Congestion and Numerical Simulation. Physical Review E, 51, 1035-1042. http://dx.doi.org/10.1103/PhysRevE.51.1035
- Hong, S.J. and Oguchi, T. (2005) Evaluation of Highway Geometric Design and Analysis of Actual Operating Speed. Journal of the Eastern Asia Society for Transportation Studies, 6, 1048-1061. http://dx.doi.org/10.1080/00423110600879395
- Sentouh, C., Glaser, S. and Mammar, S. (2006) Advanced Vehicle-Infrastructure-Driver Speed Profile for Road Departure Accident Prevention. Vehicle System Dynamics, 44, 612-623.
- Komada, K., Masukura, S. and Ngatani, T. (2009) Effect of Gravitational Force upon Traffic Flow with Gradients. Physica A, 388, 2880-2894. http://dx.doi.org/10.1016/j.physa.2009.03.029
- Komada, K., Masukura, S. and Nagatani, T. (2009) Traffic Flow on a Toll Highway with Electronic and Traditional Tollgates. Physica A, 388, 4979-4990. http://dx.doi.org/10.1016/j.physa.2009.08.019
- Watanabe, M. (2011) An Extension of Optimal-Velocity Model and Dynamical Transition in Congested Phase I. Far East Journal of Dynamical Systems, 16, 71-86.
- Watanabe, M. (2014) Extended Optimal-Velocity Model and Jam Formation Mechanism in Traffic Flow Dynamics. Hosei Journal of Humanity and Environment, 14, 139-150.

