Engineering
Vol.5 No.5A(2013), Article ID:31862,5 pages DOI:10.4236/eng.2013.55A008
I-Pre-Cauchy Double Sequences and Orlicz Functions
1Department of Mathematics, Aligarh Muslim University, Aligarh, India
2Department of Mathematics, Science and Art Faculty, Adiyaman University, Adiyaman, Turkey
3Department of Applied Mathematics, Zakir Hussain College of Engineering and Technology, Aligarh Muslim University, Aligarh, India
Email: vakhanmaths@gmail.com, nazneen4maths@gmail.com, aesi23@hotmail.com
Copyright © 2013 Vakeel A. Khan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 1, 2013; revised April 3, 2013; accepted April 12, 2013
Keywords: Ideal; Filter; Paranorm; I-Convergent; Invariant Mean; Monotone and Solid Space
ABSTRACT
Let 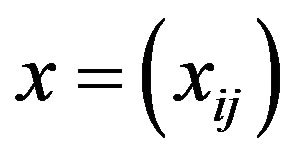 be a double sequence and let M be a bounded Orlicz function. We prove that x is I-pre-Cauchy if and only if
be a double sequence and let M be a bounded Orlicz function. We prove that x is I-pre-Cauchy if and only if 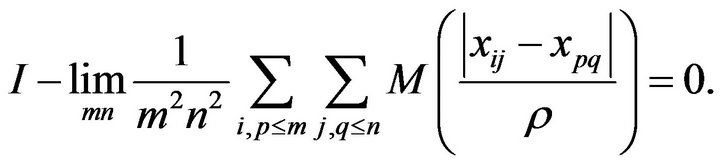 This implies a theorem due to Connor, Fridy and Klin [1], and Vakeel A. Khan and Q. M. Danish Lohani [2].
This implies a theorem due to Connor, Fridy and Klin [1], and Vakeel A. Khan and Q. M. Danish Lohani [2].
1. Introduction
The concept of statistical convergence was first defined by Steinhaus [3] at a conference held at Wroclaw University, Poland in 1949 and also independently by Fast [4], Buck [5] and Schoenberg [6] for real and complex sequences. Further this concept was studied by Salat [7], Fridy [8], Connor [9] and many others. Statistical convergence is a generalization of the usual notation of convergence that parallels the usual theory of convergence.
A sequence 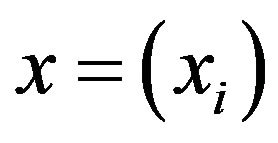 is said to be statistically convergent to
is said to be statistically convergent to ![]() if for a given
if for a given 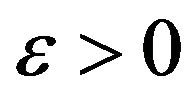
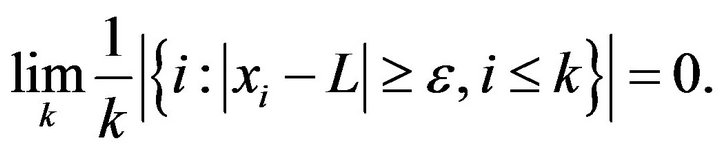
A sequence  is said to be statistically precauchy if
is said to be statistically precauchy if
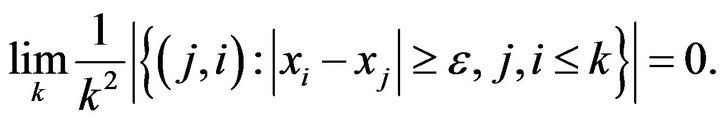
Connor, Fridy and Klin [1] proved that statistically convergent sequences are statistically pre-cauchy and any bounded statistically pre-cauchy sequence with a nowhere dense set of limit points is statistically convergent. They also gave an example showing statistically pre-cauchy sequences are not necessarily statistically convergent (see [10]).
Throughout a double sequence is denoted by 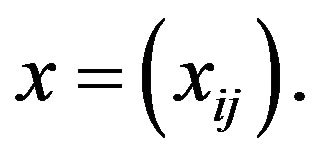 A double sequence is a double infinite array of elements
A double sequence is a double infinite array of elements  for all
for all 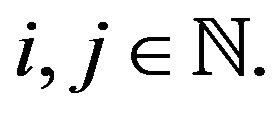
The initial works on double sequences is found in Bromwich [11], Tripathy [12], Basarir and Solancan [13] and many others.
Definition 1.1. A double sequence 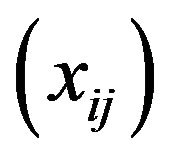 is called statistically convergent to
is called statistically convergent to ![]() if
if

where the vertical bars indicate the number of elements in the set.
Definition 1.2. A double sequence  is called statistically pre-cauchy if for every
is called statistically pre-cauchy if for every 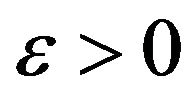 there exist
there exist 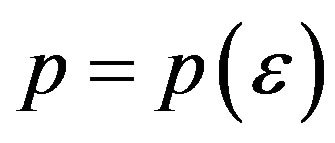 and
and 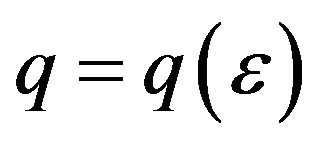 such that
such that
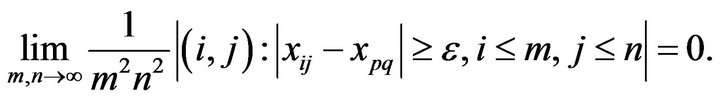
Definition 1.3. An Orlicz Function is a function  which is continuous, nondecreasing and convex with
which is continuous, nondecreasing and convex with 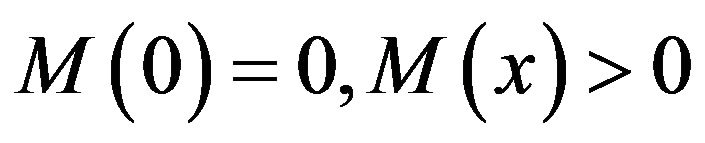 for
for 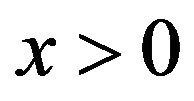 and
and , as
, as![]() .
.
If convexity of  is replaced by
is replaced by  , then it is called a Modulus function (see Maddox [14]). An Orlicz function may be bounded or unbounded. For example,
, then it is called a Modulus function (see Maddox [14]). An Orlicz function may be bounded or unbounded. For example,
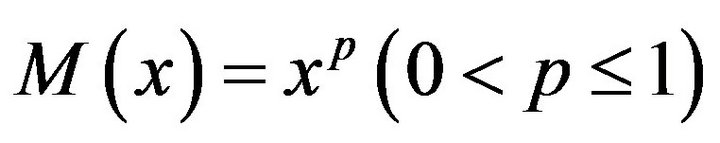 is unbounded and
is unbounded and 
is bounded (see Maddox [14]).
Lindenstrauss and Tzafriri [15] used the idea of Orlicz functions to construct the sequence space,
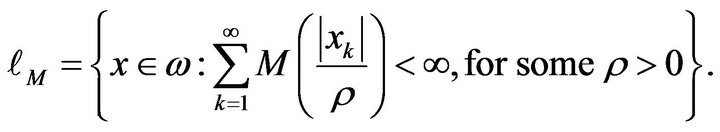
The space  is a Banach space with the norm
is a Banach space with the norm

The space 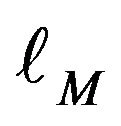 is closely related to the space
is closely related to the space 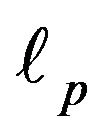 which is an Orlicz sequence space with
which is an Orlicz sequence space with 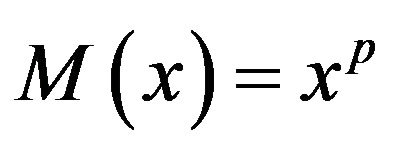 for
for .
.
An Orlicz function M is said to satisfy  condition for all values of
condition for all values of ![]() if there exists a constant
if there exists a constant 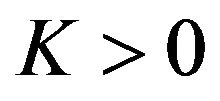 such that
such that  for all values of
for all values of 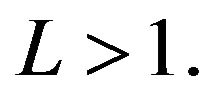
The study of Orlicz sequence spaces have been made recently by various authors [1,2,16-20]).
In [1], Connor,Fridy and Klin proved that a bounded sequence 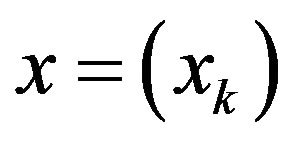 is statistically pre-cauchy if and only if
is statistically pre-cauchy if and only if

The notion of I-convergence is a generalization of statistical convergence. At the initial stage it was studied by Kostyrko, Salat, Wilezynski [21]. Later on it was studied by Salat, Tripathy, Ziman [22] and Demirci [23], Tripathy and Hazarika [24-26]. Here we give some preliminaries about the notion of I-convergence.
Definition 1.4. [20,27] Let X be a non empty set. Then a family of sets  (
(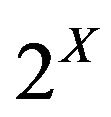 denoting the power set of X) is said to be an ideal in X if
denoting the power set of X) is said to be an ideal in X if
(i) 
(ii) I is additive i.e .
.
(iii) I is hereditary i.e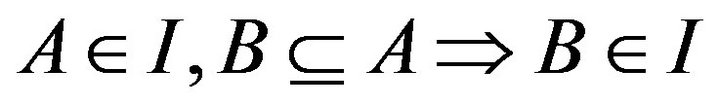 .
.
An Ideal 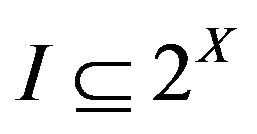 is called non-trivial if
is called non-trivial if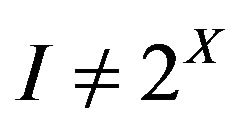 . A non-trivial ideal
. A non-trivial ideal is called admissible if
is called admissible if 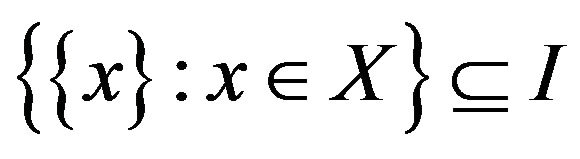 .
.
A non-trivial ideal I is maximal if there cannot exist any non-trivial ideal 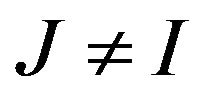 containing I as a subset.
containing I as a subset.
For each ideal I, there is a filter 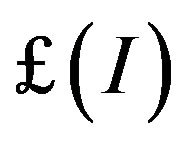 corresponding to I. i.e.
corresponding to I. i.e.

Definition 1.5. [10,21,28] A double sequence  is said to be I-convergent to a number L if for every
is said to be I-convergent to a number L if for every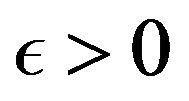 ,
,
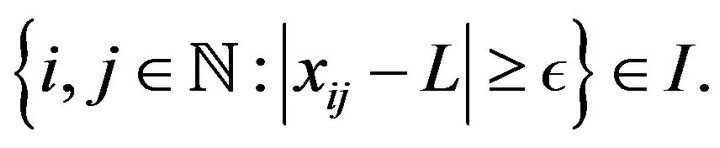
In this case we write 
Definition 1.6. [21] A non-empty family of sets 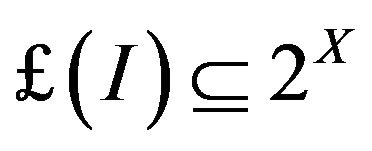 is said to be filter on X if and only if
is said to be filter on X if and only if
(i)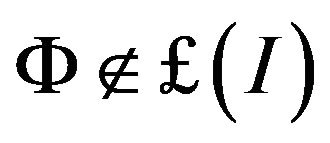 (ii) For
(ii) For 
 we have
we have 
(iii) For each  and
and  implies
implies .
.
2. Main Results
In this article we establish the criterion for any arbitrary double sequence to be I-pre-cauchy.
Theorem 2.1. Let  be a double sequence and let M be a bounded Orlicz function then
be a double sequence and let M be a bounded Orlicz function then ![]() is I-preCauchy if and only if
is I-preCauchy if and only if
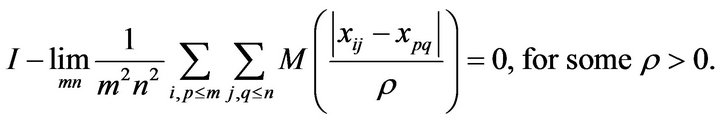
Proof: Suppose that
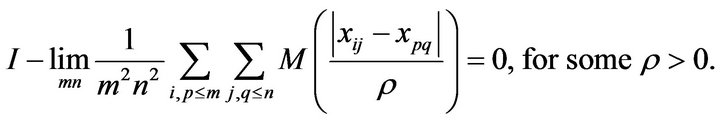
For each  and
and  we have that
we have that

(1)
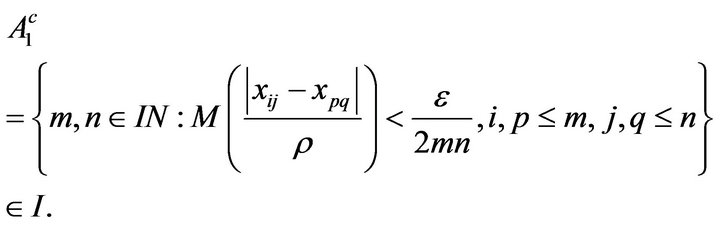
(2)
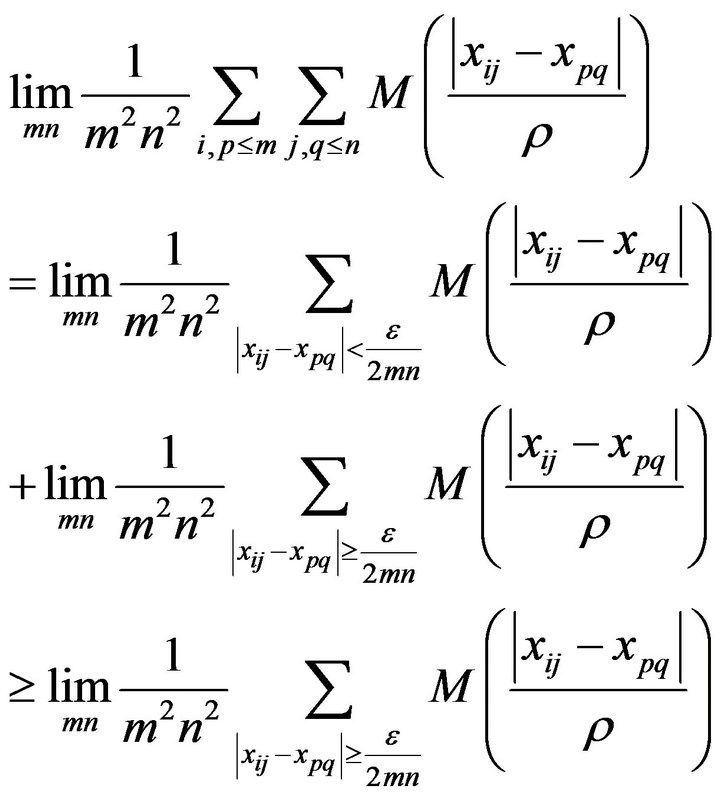
Now by (1) and (2) we have
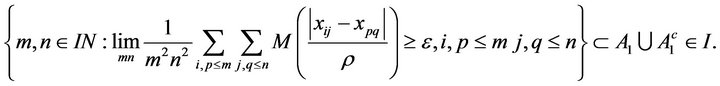
thus ![]() is I-pre-Cauchy.
is I-pre-Cauchy.
Now conversely suppose that ![]() is I-pre-Cauchy, and that
is I-pre-Cauchy, and that ![]() has been given.
has been given.
Then we have

where,
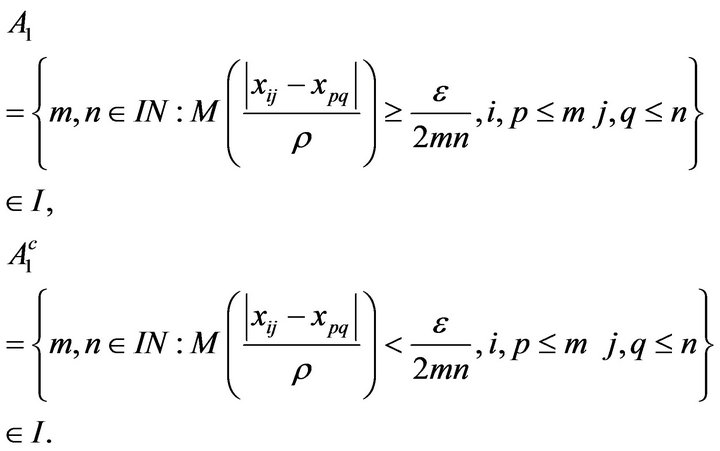
Let 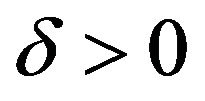 be such that
be such that 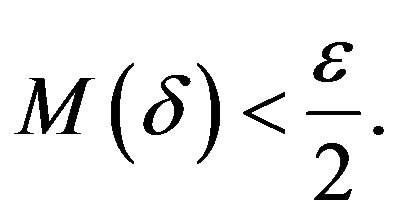 Since M is a bounded Orlicz function there exists an integer B such that
Since M is a bounded Orlicz function there exists an integer B such that 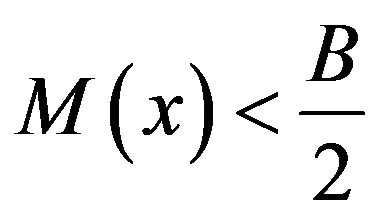 for all
for all . Therefore, for each
. Therefore, for each

(3)
Since ![]() is I-pre-Cauchy, there is an
is I-pre-Cauchy, there is an  such that the right hand side of (3) is less than
such that the right hand side of (3) is less than ![]() for all
for all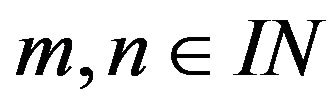 . Hence
. Hence
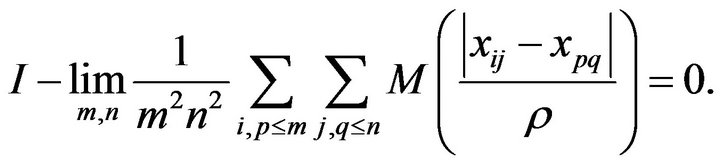
Theorem 2.2. Let 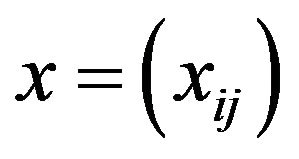 be a double sequence and let M be a bounded Orlicz function then x is I-convergent to L if and only if
be a double sequence and let M be a bounded Orlicz function then x is I-convergent to L if and only if
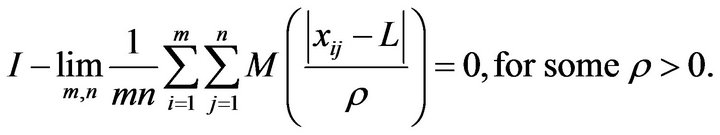
Proof: Suppose that

with an Orlicz function M, then ![]() is I-convergent to L (See [1])
is I-convergent to L (See [1])
Conversely suppose that ![]() is I-convergent to L. We can prove this in similar manner as in Theorem 2.1 assuming that
is I-convergent to L. We can prove this in similar manner as in Theorem 2.1 assuming that
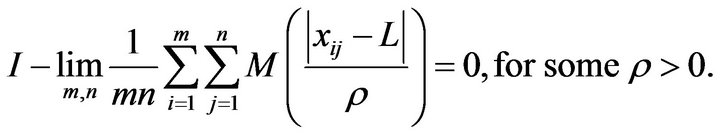
and M being a bounded Orlicz function.
Corollary 2.3. A sequence 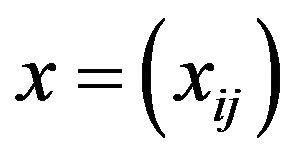 is I-convergent if and only if
is I-convergent if and only if

Proof: Let  Then
Then

Let
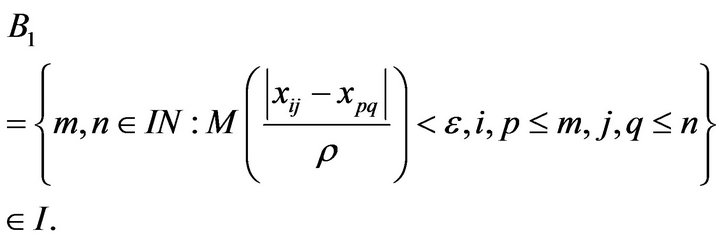 (4)
(4)
and
 (5)
(5)
Therefore from (4) and (5) we have,
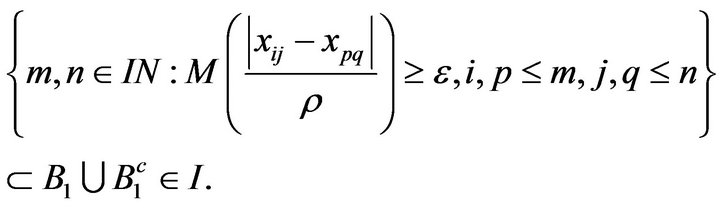
Hence
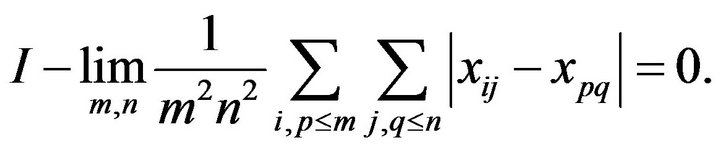
if and only if
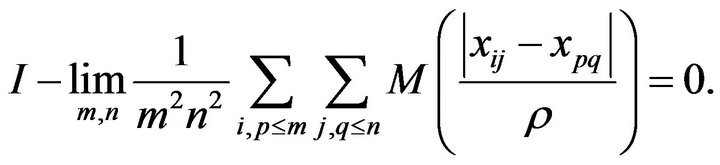
By an immediate application of Theorem 2.1 we get the desired result.
Corollary 2.4. A sequence 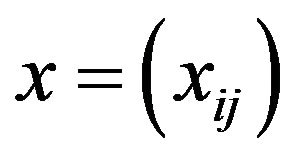 is I-convergent to L if and only if
is I-convergent to L if and only if
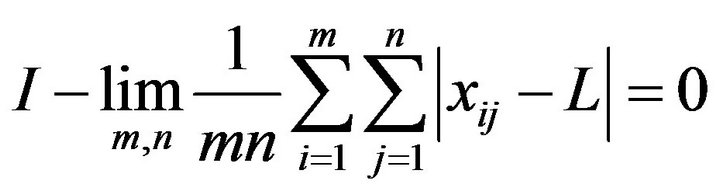
Proof: Let 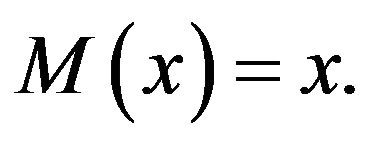
We can prove this in the similar manner as in the proof of Corollary 2.3.
3. Acknowledgements
The authors would like to record their gratitude to the reviewer for his careful reading and making some useful corrections which improved the presentation of the paper.
REFERENCES
- J. Connor, J. A. Fridy and J. Kline, “Statistically PreCauchy Sequence,” Analysis, Vol. 14, 1994, pp. 311-317.
- A. K. Vakeel and Q. M. Danish Lohani, “Statistically Pre-Cauchy Sequences and Orlicz Functions,” Southeast Asian Bulletin of Mathematics, Vol. 31, No. 6, 2007, pp. 1107-1112.
- H. Steinhaus, “Sur la Convergence Ordinaire et la Convergence Asymptotique,” Colloquium Mathematicum, Vol. 2, 1951, pp. 73-74.
- H. Fast, “Sur la Convergence Statistique,” Colloquium Mathematicum, Vol. 2, 1951, pp. 241-244.
- R. C. Buck, “Generalized Asymptotic Density,” American Journal of Mathematics, Vol. 75, No. 2, 1953, pp. 335- 346.
- I. J. Schoenberg, “The Integrability of Certain Functions and Related Summability Methods,” The American Mathematical Monthly, Vol. 66, 1959, pp. 361-375.
- T. Salat, “On Statistically Convergent Sequences of Real Numbers,” Mathematica Slovaca, Vol. 30, 1980, pp. 139- 150.
- J. A. Fridy, “On Statistical Convergence,” Analysis, Vol 5, 1985, pp. 301-311.
- J. S. Connor, “The Statistical and Strong P-Cesaro Convergence of Sequences,” Analysis, Vol. 8, 1988, pp. 47- 63.
- M. Gurdal, “Statistically Pre-Cauchy Sequences and Bounded Moduli,” Acta et Commentationes Universitatis Tarytensis de Mathematica, Vol. 7, 2003, pp. 3-7.
- T. J. I. Bromwich, “An Introduction to the Theory of Infinite Series,” MacMillan and Co. Ltd., New York, 1965.
- B. C. Tripathy, “Statistically Convergent Double Sequences,” Tamkang Journal of Mathematics, Vol. 32, No. 2, 2006, pp. 211-221.
- M. Basarir and O. Solancan, “On Some Double Seuence Spaces,” The Journal of The Indian Academy of Mathematics, Vol. 21, No. 2, 1999, pp. 193-200.
- I. J. Maddox, “Elements of Functional Analysis,” Cambridge University Press, Cambridge, Cambridge, 1970.
- J. Lindenstrauss and L. Tzafriri, “On Orlicz Sequence Spaces,” Israel Journal of Mathematics, Vol. 10, No. 3, 1971, pp. 379-390. doi:10.1007/BF02771656
- M. Et, “On Some New Orlicz Sequence Spaces,” Journal of Analysis, Vol. 9, 2001, pp. 21-28.
- S. D. Parashar and B. Choudhary, “Sequence Spaces Defined by Orlicz Function,” Indian Journal of Pure and Applied Mathematics, Vol. 25, 1994, pp. 419-428.
- B. C. Tripathy and Mahantas, “On a Class of Sequences Related to the lp Space Defined by the Orlicz Functions,” Soochow Journal of Mathematics, Vol. 29, No. 4, 2003, pp. 379-391.
- A. K. Vakeel and S. Tabassum, “Statistically Pre-Cauchy Double Sequences and Orlicz Functions,” Southeast Asian Bulletin of Mathematics, Vol. 36, No. 2, 2012, pp. 249-254.
- A. K. Vakeel, K. Ebadullah and A Ahmad, “I-Pre-Cauchy Sequences and Orlicz Functions,” Journal of Mathematical Analysis, Vol. 3, No. 1, 2012, pp. 21-26.
- P. Kostyrko, T. Salat and W. Wilczynski, “I-Convergence,” Real Analysis Exchange, Vol. 26, No. 2, 2000, pp. 669-686.
- T. Salat, B. C. Tripathy and M. Ziman, “On Some Properties of I-Convergence,” Tatra Mountains Mathematical Publications, Vol. 28, 2004, pp. 279-286.
- K. Demirci, “I-Limit Superior and Limit Inferior,” Mathematical Communications, Vol. 6, 2001, pp. 165-172.
- B. C. Tripathy and B. Hazarika, “Paranorm I-Convergent Sequence Spaces,” Mathematica Slovaca, Vol. 59, No. 4, 2009, pp. 485-494. doi:10.2478/s12175-009-0141-4
- B. C. Tripathy and B. Hazarika, “Some I-Convergent Sequence Spaces Defined by Orlicz Function,” Acta Mathematica Applicatae Sinica, Vol. 27, No. 1, 2011, pp. 149- 154. doi:10.1007/s10255-011-0048-z
- B. C. Tripathy and B. Hazarika, “I-Monotonic and I-Convergent Sequences,” Kyungpook Mathematical Journal, Vol. 51, No. 2, 2011, pp. 233-239. doi:10.5666/KMJ.2011.51.2.233
- A. K. Vakeel, K. Ebadullah and S. Suthep, “On a New I-Convergent Sequence Spaces,” Analysis, Vol. 32, No. 3, 2012, pp. 199-208. doi:10.1524/anly.2012.1148
- M. Gurdal and M. B. Huban, “On I-Convergence of Double Sequences in the Topology induced by Random 2- Norms,” Matematicki Vesnik, Vol. 65, No. 3, 2013, pp. 1-13.

