Engineering
Vol.4 No.11(2012), Article ID:24532,4 pages DOI:10.4236/eng.2012.411098
Burst Error Correction Method Based on Arithmetic Weighted Checksums
1Department of Engineering, Amman Private University, Amman, Jordan
2Department of Information Technology, Al-Balqa Applied University, Irbid, Jordan
Email: salehalomar@yahoo.com
Received July 19, 2012; revised August 23, 2012; accepted September 4, 2012
Keywords: Burst-Errors; Reed Solomon; Arithmetic Weighted Checksum
ABSTRACT
In this paper a new approach for increasing the performance of burst error correction that occurs during data transmission in low-frequency channels with pulse-code modulation is proposed. The specific technique is based on the weighted checksum which is computed with arithmetic operations. It is shown that the solution proposed not only guarantees the correction of any single error burst but it also lowers the computational complexity so that procedure correction time does not depend on controlled data block length. Finally, the use of the algorithm is illustrated via the thorough presentation of an example of erroneous data transmission.
1. Introduction
The development of the information transmission technologies in the computer networks and in the telecommunication systems is inseparably connected with the problem of integrity and of ensuring high effectiveness of error detection and correction of errors which occur during data transmission.
The dynamic increase in the speed of information transmission in the buses of computer systems and the channels of computer networks brings about stringent requirements for the performance of the hardware implementation of the error detection and correction algorithm: it must ensure the realization of the operations which are connected with the rate of error detection for data transmission.
A continuous increase in the speeds of data transmission in the telecommunications network systems is resulted in change of error character and effectiveness criterions of error detecting and correction. Today the main cause of data transmission errors is external impulse noise [1]. Data transmission speeds up the external impulse noise’s influence on few adjacent channels signals. In consequence, the group of adjacent bits of transmitted data can be distorting. Such group of bits is named burst of errors. So, today bursts of bits distortions become dominating type of errors [1].
On the other hand, the dynamic increase of the data transmission speed has changed the importance such of tradition error control effectiveness criterions as number control bits and possibilities of detecting and correction errors in rate data transmission. It is clear that in modern condition of significant speeding up of data transmission, its increasing of the importance of computation complexity of detecting and correction errors procedure which impose the possibilities of real time error control. On the contrary, the modern tendency for increase of speed and values of data transmission decreases the importance of such tradition error control effectiveness criterions as number control bits.
Thus, the problem of detecting and correcting burst of errors in rate data transmission is very important and requires attention for the current and future technological developments in computer and telecommunications system. This specifies the urgency and the practical importance of the development of new methods and means to speed up the burst errors detection and correction procedures.
2. Burst Error Analysis and Existing Techniques for Their Correction
The errors that arise during data transmission in lowfrequency channels with pulse-code modulation are caused by two types of sources: internal and external. Among the internal data transmission error sources are thermal noise that is present in every electronic device. Noise or interference signals are caused by events external to the transmission path (solar flares affecting satellite electronics or radio waves, heavy electrical machinery etc.), frequency, amplitude, or phase distortion of the transmitted signal [2].
Unlike the errors that are caused by thermal noise, all other sources tend to give errors that formulate bursts. About the frequency of the error events only empirical conclusions can be drawn by testing under real conditions.
The term burst errors suggest that those errors are correlated, i.e. if one bit is erroneous, it is quite likely that the adjacent bits have also been corrupted. When one refers to the term burst error of size m, what is meant is that the distance in bits from the first to the last error in the frame is at most m – 1 while the intermediate bits may or may not be corrupted.
Indeed, let the externally produced noise correspond to a maximum duration tn. One thing worth mentioning is that for the same bit error rate, burst errors are in principle easier to deal with than random errors. For example, consider the case of frames consisted of 1000 bits and an overall error rate of 1 in 1000. If all errors were random, almost all frames would be corrupted. However, if dealing with burst error events of size 1000, only 1 frame in 1000 would be corrupted [3]. The disadvantage that comes with the appearance of burst error events is that error detection and correction as well as analytical modeling of the specific patterns is much more difficult to achieve compared with the case of random errors.
When random error is the case, the theoretical model of the less memory Binary Symmetric Channel (BSC) is being used. The BSC is not appropriate for the description of burst error events as a channel with memory is necessary [4].
The probability that two burst errors occur is lower than the probability of the occurrence of a singular burst error. Thus, burst error multiplicity is usually considered to be equal to one in the state of the art.
With the use of special coding it is possible to distinguish two approaches for the control of the appearing errors:
• The error detection by special codes and their correction by retransmitting the data block (ARQ—Automatic Repeat Request);
• The correction of the appearing errors by applying correcting codes without the repeated transmission (FEC—Forward Error Correction).
The choice of the appropriate technology is determined by the features of the data transmission channel as well as the particularities of the specific use. Thus, in wired systems for digital data transmission, in which the intensity of errors is several orders lower in comparison with the wireless channels, the use of ARQ is considered to be more effective. On the contrary, in the wireless channels the prevailing source of the transmitted errors is the externally produced noise and in this case the intensity of the appearing errors is high enough to consider the application of FEC technologies to be more preferable.
In general, ARQ technology is being preferred over FEC technology as the latter demands more complicated decoding hardware and greater redundancy. This makes sense if one takes into consideration that FEC technology demands not only the knowledge of the occurrence of at least one error but also of the exact number of erroneous bits and of course of the exact positions of the corrupted bits in the affected block. Therefore, the drawbacks of error correction codes include the relatively large volume of control information, the complexity of the procedures and the decoding process. As a matter of fact, the number of control bits increases exponentially as the multiplicity of errors that are required to be corrected increases. Additionally, in the case of correction codes the computations for the syndrome calculation take place even if no corruption has occurred and that causes a considerable cost in complexity [3].
For burst error correction usually the cyclic codes are utilized. Among cyclic codes which are peculated to one burs error correction, Fire, Abramson and Melay-Abramson codes [2] can be mentioned. At the same time the most widespread is Reed-Solomon code [4] which is able to correct few burst errors. In practice, the type ReedSolomon code for one burs error correction is most frequently used.
Reed-Solomon code is non-binary codes suggests the division of the transmitted block into n symbols, each of which will be consisted of m bit. With the use of 2 × h control symbols a Reed-Solomon code allows the correction of every distorted bit in h symbols. However the computational complexity of the implementation of the demanded calculations is unjustifiably large. From the mathematical point of view, the procedure of distorted symbol location consists of solving of nonlinear system equations. In fact according to Reed-Solomon code techniques for this nonlinear system equations solving use enumeration: finding of nonzero components error location vector executed by examining all n variants. It means that computational complexity of procedures coding, decoding and error correction depend on transmitted block length.
Usually, both encoding and decoding procedures are implemented with specific devices and since Reed-Solomon codes are cyclic, encoding as well as error control are implemented in a sequential way, namely without the ability of parallel computations. Finally, since ReedSolomon codes compute the syndromes whether there is an error or not, computational cost increases even more.
Let us consider that the burst error is localized in a specific symbol. This is the exact case where code ReedSolomon theoretically minimizes the number of control digits to use. However, the occurrence of a burst error in low frequency channels or during data storage has several further crucial features and those particular features allow the proposed method to maximize its efficiency in burst error correction compared to Reed-Solomon codes. For the correction of this kind of errors, Reed-Solomon codes must be able to guarantee the correction of h = 2 × r—bit symbols, since the burst error could originate anywhere in the sequence. Consequently, the total number of control symbols required in the case of Reed-Solomon is equal to 4 (4 × m bits) while the theoretical minimum is 2 × r bits. That implies that Reed-Solomon code is clearly suboptimal for the solution of the problem under study.
Another approach over the last years is the use of simple weighted checksum for error correction [3]. The based on logical weighted checksum approach for single burst error correction [3] is more effective in comparison to Reed-Solomon codes: used less control bits, this approach allowed to reduce computation complexity from 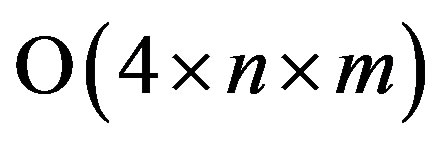 to
to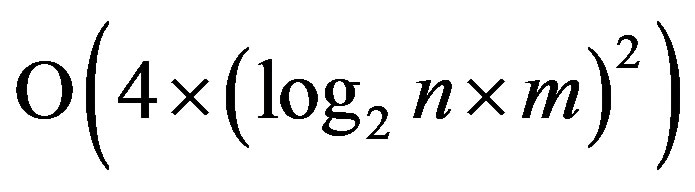 . Using logical weighted checksum approach enhances the efficiency of single burst error control in low frequency channels, due to the decomposition of the main problem in two parts: the localization of the positions of the corrupted bits in the burst and the localization of the start point of the burst that has occurred.
. Using logical weighted checksum approach enhances the efficiency of single burst error control in low frequency channels, due to the decomposition of the main problem in two parts: the localization of the positions of the corrupted bits in the burst and the localization of the start point of the burst that has occurred.
From the modern effectiveness criterions, the main disadvantage of logical weighted checksum method consists in that computation complexity of burst error correction procedure depends on transmitted block length.
The aim of presented investigation is to speed up the burst error correction procedure so that it can be executed in rate data transmission.
3. Burst Error Correction
Let us consider a transmitted information block B that consists of N bits:
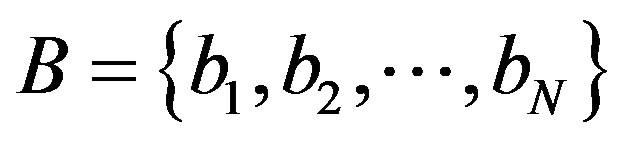 ,
,
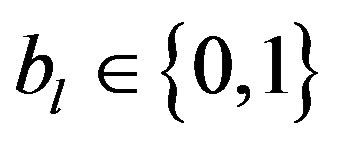 .
.
Proposed method assumes that this block divided into n symbols: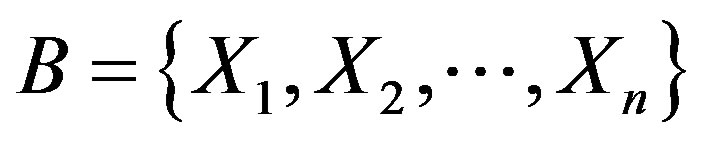 . Every j-th symbol Xj,
. Every j-th symbol Xj, 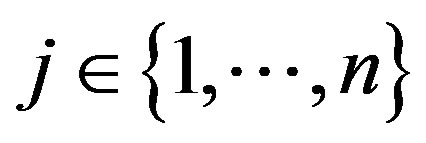 contain m bits
contain m bits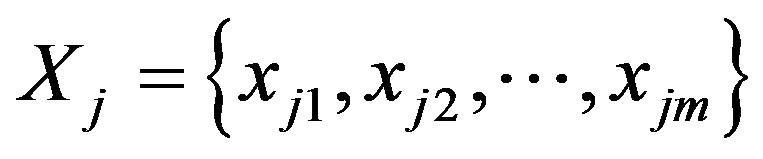 , so that
, so that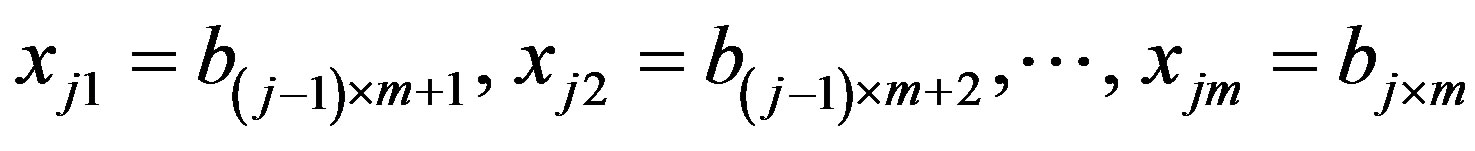 , where m is the maximum size of the burst. Each one j-th symbol Xj can be considered as binary number
, where m is the maximum size of the burst. Each one j-th symbol Xj can be considered as binary number 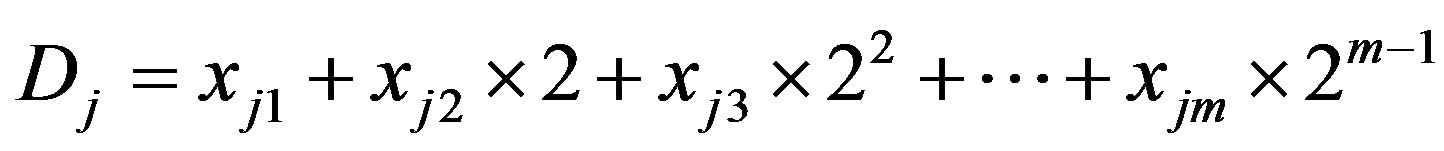 . For every j-th symbol Xj there is weight coefficient Wj defined as
. For every j-th symbol Xj there is weight coefficient Wj defined as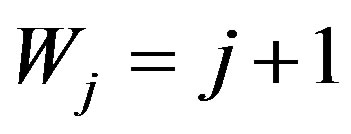 .
.
The control code C consists of three components C = {C1, C2, C3}, first of which—C1 is the arithmetic sum of odd-numbered symbols of the transmitted block:
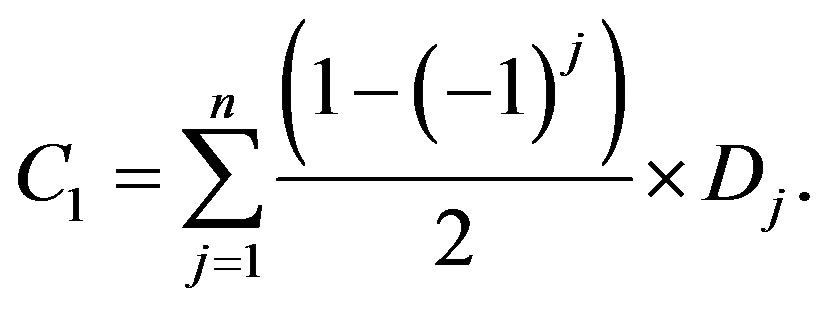 (1)
(1)
Second component С2 is calculated as arithmetic sum of symbols with even number in transmitted block:
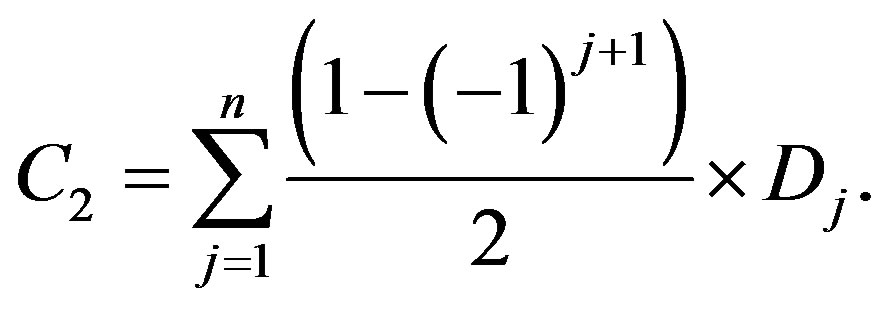 (2)
(2)
The third component C3 is the arithmetic sum of products symbols by its weight coefficients, whose are by one greater of symbols number:
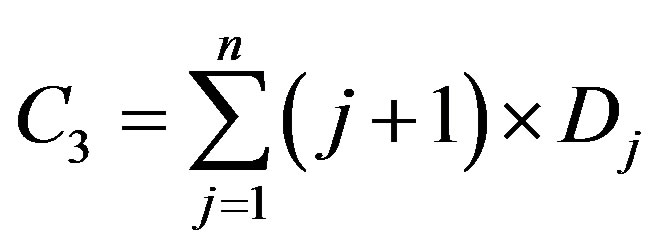 (3)
(3)
The mentioned above control code components calculated according to Equations (1)-(3) by sender are denoted as C1S, C2S and C3S. After the calculation of the control code at the sender side, this information is sent to the receiver in the following order: C3S, C1S, C2S, X1, X2,···, Xn.
For example, let us consider the data block B which consists of 16 bits (N = 16) B = {1001 1010 1100 101}. If maximal number m of bits if burst equals 4 (m = 4), transmitted block divides into four (n = 4) 4-bit symbols: X1 = {1001}, X2 = {0111}, X3 = {1111}, X4 = {1010}. Correspondently: D1 = 9, D2 = 14, D3 = 15, D4 = 5. On the sender side the components of the control code will be computed as such:
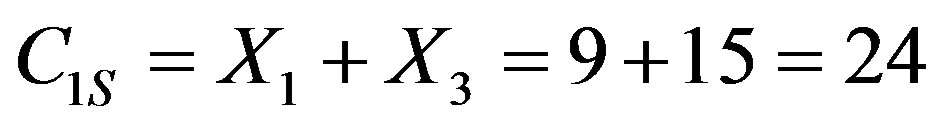 ;
; 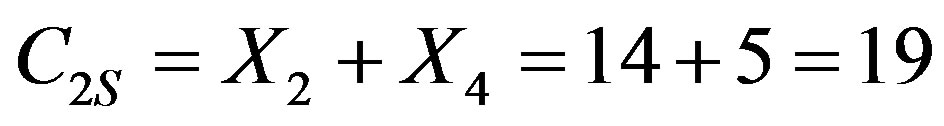 ;
; 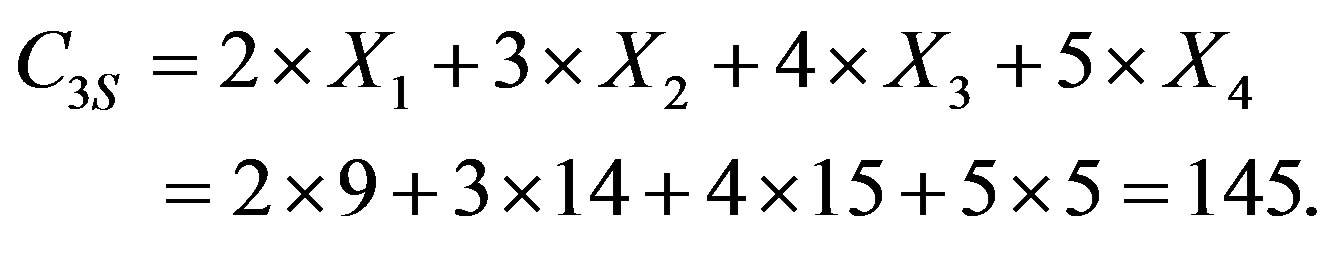
Sender sent to the receiver following bits sequences: C3S, C1S, C2S, X1, X2,···, Xn = 1000100 00110 01010 1001 0111 1111 1010.
On the receiver side the information block and senders control code are received and using Equations (1)-(3) the receiver control code components denoted as C1R, C2R and C3R are calculated. The receiver calculates the difference Δ using the three components computed in their end and those that were received. Indeed, D =
Consequently, the receiver analyses the code D for the purpose of determining if the information block was transmitted without errors, for the detection of possible transmission errors in the information block and for the correction of such errors. Assuming that only a single burst of errors occurs and that this burst distorts no more than tree symbols, there may occur one of the following cases:
1) If all three components of code Δ are equal to zero, namely D1 = 0, D3 and D3 = 0, then the information block has been transmitted without errors.
2) One or pair of adjacent symbols of information block B = {X1, X2,···, Xn} are distorted.
3) Control code component C2S and first symbols X1 of information block are distorted.
4) One or pair of adjacent control code components C2S, C1S, C3S are distorted.
In second and third cases it is necessary to correct error in information block. In last case it would suffice to determinate this type of errors.
In second and third cases there are two different variants: only one symbol Xv is distorted and two adjacent symbols Xv and Xv +1 are distorted. If only one v-th symbol Xv is distorted and its number v is odd than 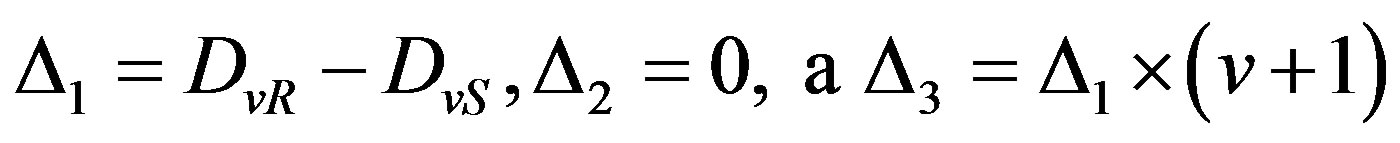 . Consequently number v can be defined by following way:
. Consequently number v can be defined by following way:
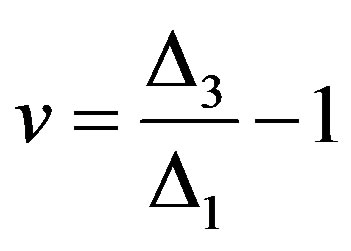 (4)
(4)
Correction is executed by following way: 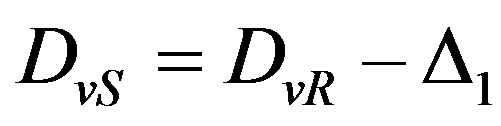 . In a similar manner the one symbol with even number in block is corrected.
. In a similar manner the one symbol with even number in block is corrected.
When two adjacent symbols Xv and Xv +1 are distorted and v is odd than
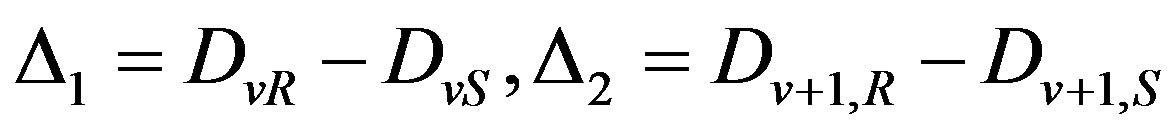
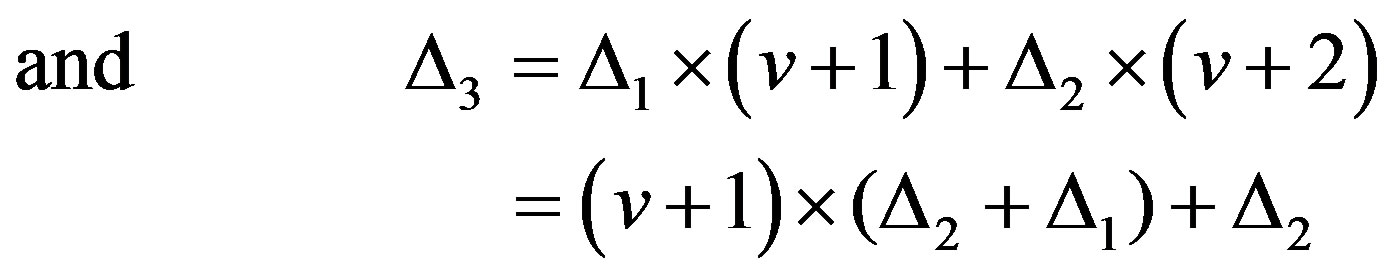
Such as in symbol Xv the high bits are distorted and in next symbol Xv+1 the low ones, condition 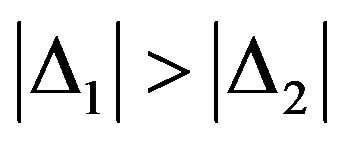 is fulfilled. In view to above number v of first distorted symbol can be define by following way:
is fulfilled. In view to above number v of first distorted symbol can be define by following way:
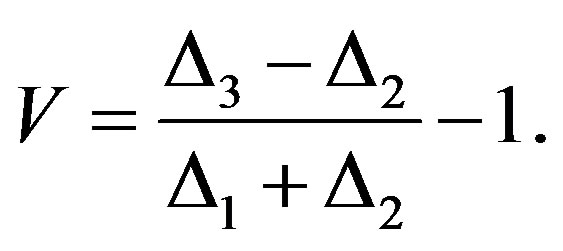 (5)
(5)
For correction of distorted symbols, it is need to execute operation: 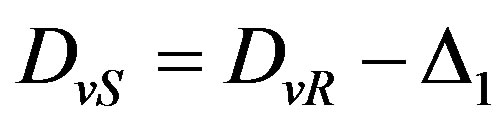 and
and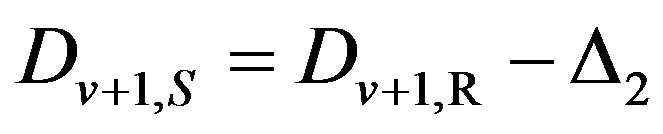 .
.
In a similar manner if v is even: 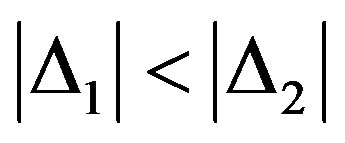 and number v of first distorted symbol can be defined by following way:
and number v of first distorted symbol can be defined by following way:
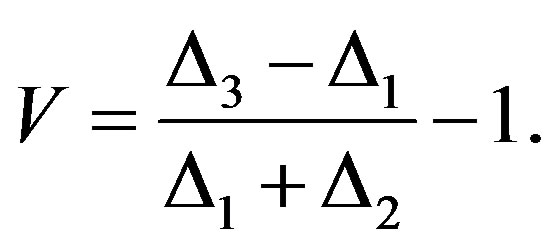 (6)
(6)
For correction of distorted symbols, it is need to execute operation: 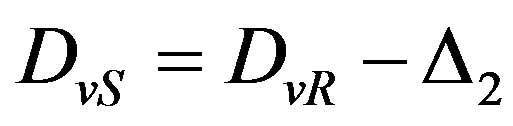 and
and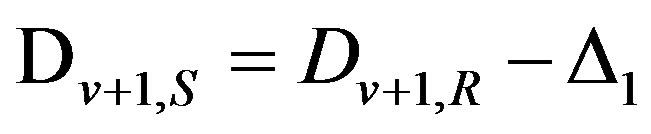 .
.
The outlined way for burst error correction can be illustrated by such example. It is suggested that during bits sequences transmission: C3S, C1S, C2S, X1S, X2S,···, XnS = 1000100 00110 01010 1001 0111 1111 1010 external noise caused a burst of errors that corrupted third and fourth symbol of information block. As a result, the corrupted symbols have been received on receiver side, which are as: X3R = {1010}, X4R = {0010}. Correspondently D1R = 9, D2R = 14, D3R = 5, D4R = 4. Consequently, on the receiver side the components of the control code will be computed as such:
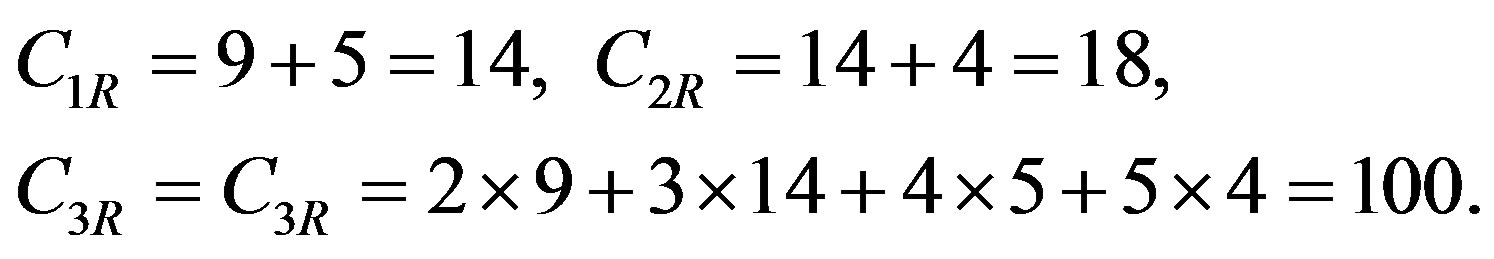
The difference of control code is calculated on receiver side as:
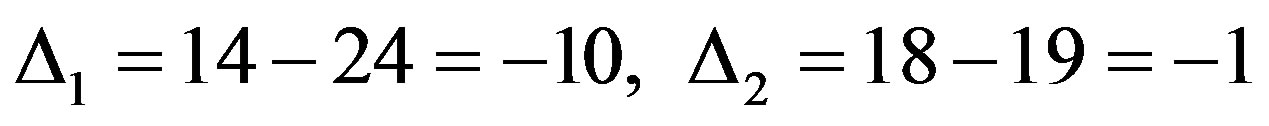
and 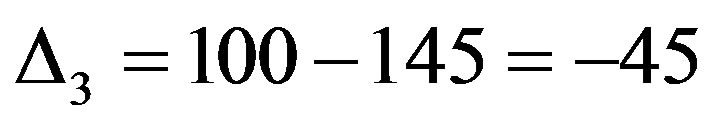 .
.
Because of 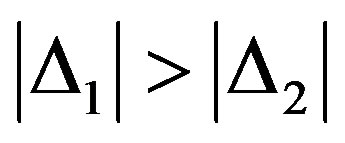 then first distorted symbol has odd number v, which according to (5) is calculated as:
then first distorted symbol has odd number v, which according to (5) is calculated as:
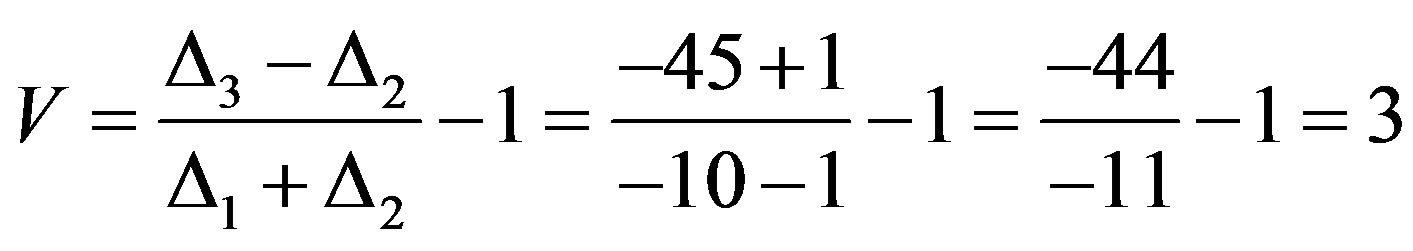
Procedure correction of X3 and X4 executed by calculation:
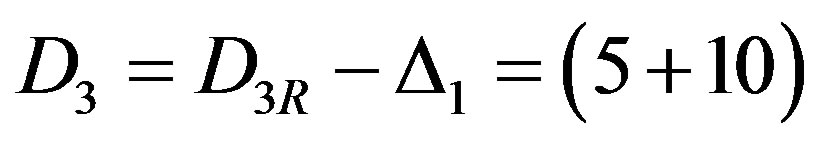 mod 25 = 15,
mod 25 = 15,
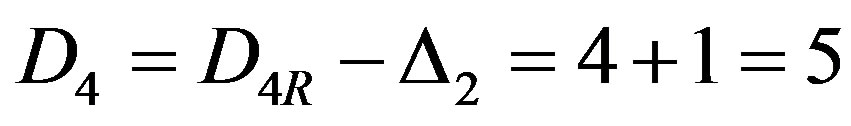 .
.
If control code component C2S and first symbols X1 of information block are distorted then D1 ¹ 0, D2 ¹ 0 and D3 ¹ 0, despite the fact that 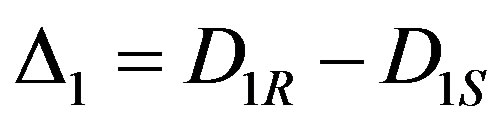 and
and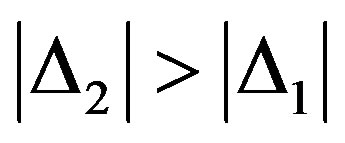 , D3 ¹ D1 × 2. If all mentioned conditions are fulfilled then correction executed by the way:
, D3 ¹ D1 × 2. If all mentioned conditions are fulfilled then correction executed by the way: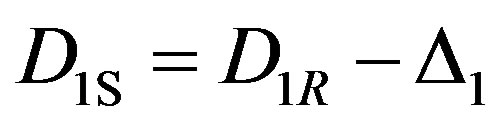 .
.
If only one of control code components C2S, C1S or C3S is distorted that two from codes D1, D2 and D3 equal to zero and one is not equal to zero. This situation can not be arising in case information symbol distorting and so can be easily defined.
In the case that pair of control components are distorted during transmission there are two variants: pair C2S, or pair C3S, C1S is distorted. In first variant D1 ¹ 0, D2 ¹ 0 and D3 ¹ 0, it is clear that such situation can not be arising in case information symbol distorting and so can be easily defined.
In second variant D3 ¹ 0, D1 ¹ 0 and D2 ¹ 0. Because C3S is transmitted before C1S, in component C3S the high bits are distorted and in component C1S the low bits are distorted. It means that 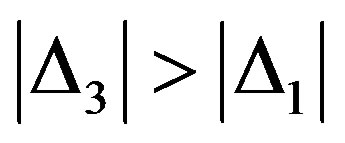 and it’s simply to show that:
and it’s simply to show that:
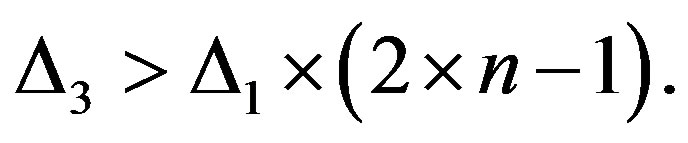 (7)
(7)
It is clear that in case distorting of information symbol occurs, the condition (7) can not be fulfilled, so this condition can be used to define the situation when pair C3S, C1S is distorted.
4. Effectiveness Estimation
As mentioned above, the main effectiveness criterions for means error correction are: number of needing control bits and computational complexity of coding, decoding and error correction procedures. The computational complexity and time complexity define the time which is needed for error control and correction.
For proposed burst error correction method number k control bits is determined by the sum of size of control code components C1, C2 and C3. It is clear that maximal value of C1 and C2 is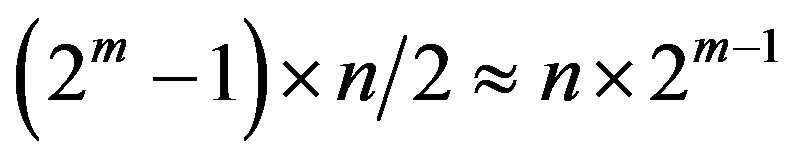 . Thus, bit size of control code components C1, C2 is equal:
. Thus, bit size of control code components C1, C2 is equal: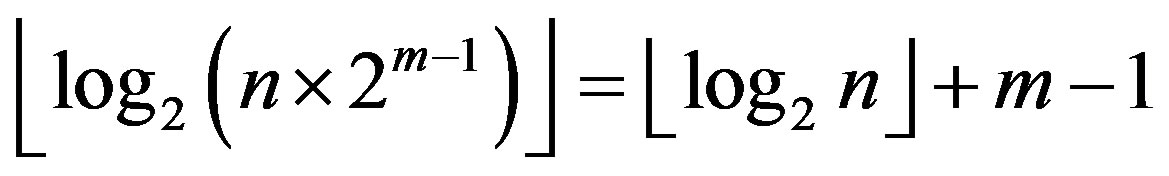 . Maximal possible value of components C3 is equal:
. Maximal possible value of components C3 is equal:
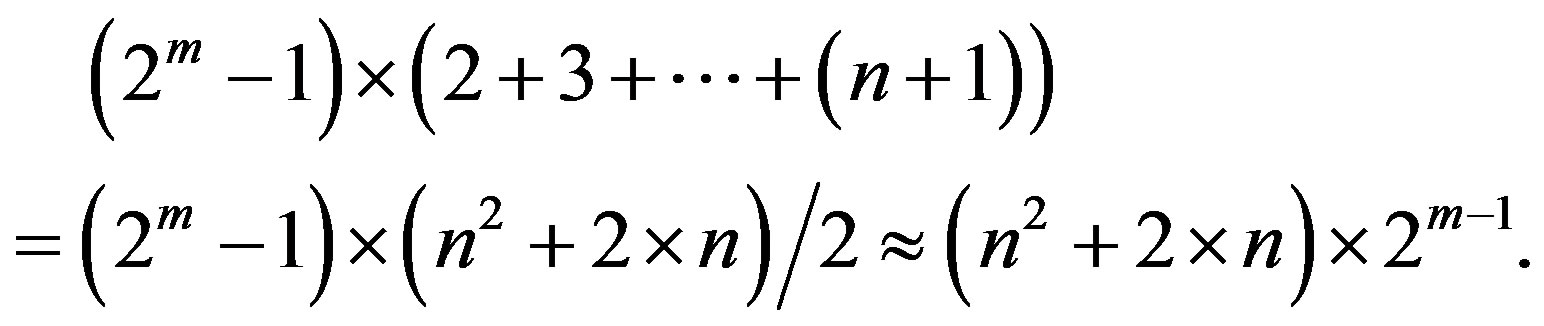
Correspondently, bit size of components C3 is equal
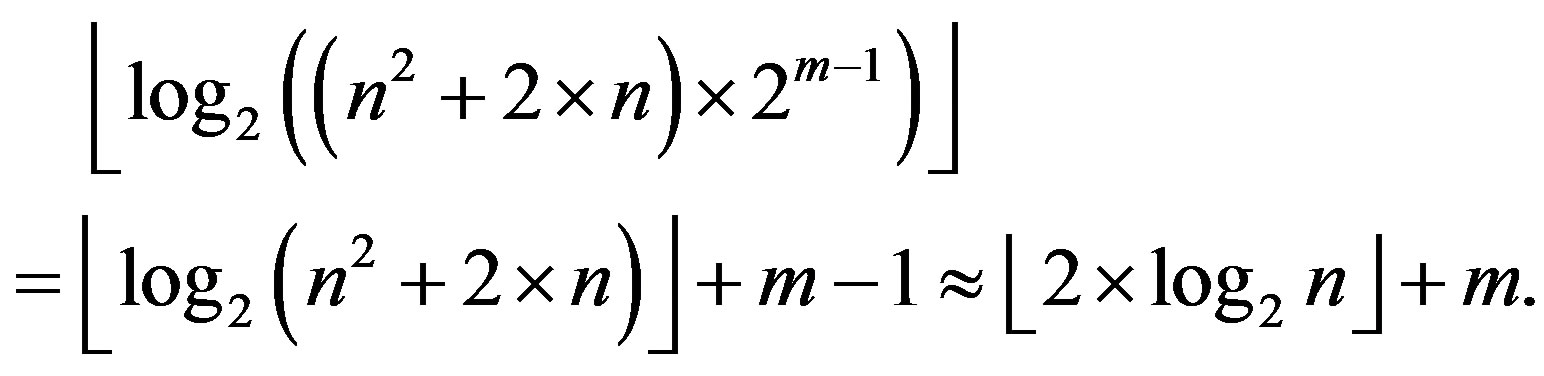
Thus, the control bits number k is equal:
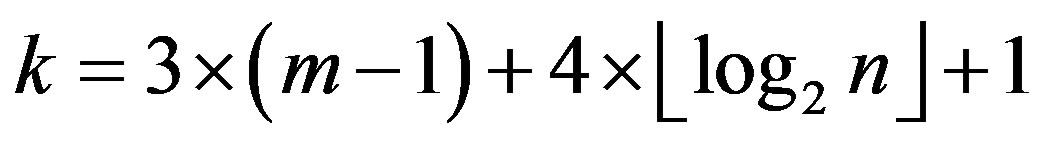 (8)
(8)
For Reed-Solomon codes which are also used for the solution of similar problems, the correction of a single burst error of size up to m bits in low-frequency channels demands 4 × m control bits.
The comparison of the two methods shows that the suggested one requires a trifle over control bits in comparison to Reed-Solomon codes. For example, for the correction of a burst error the size of which is up to 8 (m = 8) in a packet of size 64 bytes (n = 64), with the use of Reed-Solomon 4 × m = 32 bits are required while with the proposed method 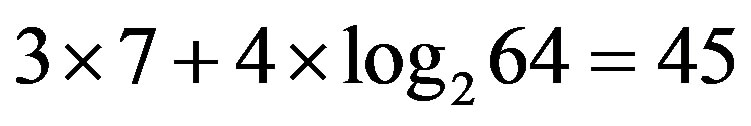 control bits are used or 40% higher than Reed-Solomon codes need.
control bits are used or 40% higher than Reed-Solomon codes need.
Additionally, Reed-Solomon codes put restrictions on the size n of the controlled information block B depending on the value of m. Thus, the block size must be up to 2m symbols or 2m × m bits. For instance, when m = 4 the information block size cannot exceed 8 bytes. On the contrary, the suggested technique which is based on the decomposition of the initial problem into the sub-problem of the localization of the burst and the sub-problem of the distribution of the errors in the burst guarantees single burst error correction without putting restriction on the size of the information block.
Finally, in Reed-Solomon codes there is lack of a control mechanism of the occurrence of errors of multiplicity higher than the one which allows correction. For instance, in case of the occurrence of two burst errors, the code proceeds to an erroneous correction of an undistorted symbol. On the contrary, for the method described above there is a control mechanism of the errors that cannot be corrected so as to alert the user to request retransmission.
The primary advantage of the proposed method is the efficient correction of single burst errors with an implementation that demands low computational complexity both for the control and the error correction.
For coding (control code components calculation), it needs to execute three addition and one multiplication per symbols of block. In view of the fact that modern processors contain the fast multiplier, it can be conceded that there are executed four operations per symbol. So, coding computational complexity—O(4 × n). In proposed method is similar to coding and, correspondently, complexity of decoding procedure—O(4 × n). For single burst error correction according to (4)-(6) is required four operation of addition and one operation of division. Eventually, for correction only five processors operation are required. It means that for burst error correction operation time does not depend on both information block length and symbol length.
Reed-Solomon code single burst error correction includes such procedures:
1) Solving of the system of two symbols equation for locator error vector coefficient define.
2) Location of the position of two distorted symbols in data block. To do this, it would require searching nonzero values of location error vector by enumeration n possible variants.
3) Solving the system of symbols equation for location distorted bits for every distorted symbol.
The total number of processors operation is equal 4 × n × m. For example, for the correction of a burst error the size of which is up to 8 (m = 8) in block of size 64 bytes (n = 64), with the use of Reed-Solomon 4 × n × m = 2048 processors operations are required while with the proposed method only five that is less than Reed-Solomon codes by factor 410. The data for comparison analysis of computation and time complexity proposed method and Reed-Solomon codes are shown in Table 1.

Table 1. Computational/time complexity both methods.
The data analysis based on Table 1 shows that the use of the method based on checksum allows the substantial reduction of time complexity compared to Reed-Solomon code. Consequently, an increase of the speed of the encoding, decoding and error correction has been achieved.
5. Conclusions
The proposed approach enhances the efficiency of single burst error control in low frequency channels due to the decomposition of the main problem in two parts: the localization of the positions of the corrupted bits in the burst and the localization of the start point of the burst that has occurred. To succeed in reducing computational complexity and speeding up processes involved, the present technique suggests the use of a conventional checksum method and the use of the weighted version of the checksum for the solution of the first and the second problem respectively.
The main advantage of proposed approach is that procedure burst error correction has computational complexity less than Reed-Solomon codes by 2 - 3 order and less that method based on logical weighted checksum by one order. It means that proposed approach assures significant speeding up of burst error correction in comparison to known methods. In doing so, required control bits number increase shall be no more 45%.
It has been shown that the application of the method described in this paper lowers the computational cost of the operations that need to be executed for the correction of the burst error comparing to Reed-Solomon codes.
REFERENCES
- B. Sklar, “Digital Communication, Fundamental and Application,” Prentice Hall, Upper Saddle River, 2001, p. 1104.
- R. E. Blahut, “Theory and Practice of Error Control Codes,” Addison-Wesley Publishing Company, Boston, 1983, p. 452.
- N. G. Bardis, O. Markovskyi and N. Doukas, “Efficient Burst Error Correction Method for Application in Low Frequency Channels and Data Storage Units,” Proceedings of IEEE Digital Signal Processing Conference, Corfu, 6-8 July 2011, pp. 1-6.
- S. B. Wickers and V. K. Bhargava, “Reed-Solomon Codes and Their Applications,” IEEE Press, Piscataway, 1983, p. 433.

