Engineering
Vol. 3 No. 12 (2011) , Article ID: 9211 , 10 pages DOI:10.4236/eng.2011.312149
Radiation Effects on Free Convection Flow Near a Vertical Plate with Ramped Wall Temperature
1Department of Mathematics, Gauhati University, Guwahati, India
2Department of Mathematics, Jagannath Barooah College, Jorhat, India
E-mail: rkdgu@yahoo.com, skdas_jrt@yahoo.co.in
Received August 15, 2011; revised September 28, 2011; accepted October 10, 2011
Keywords: Natural Convection, Ramped Wall Temperature, Radiation
ABSTRACT
The effect of radiation on the unsteady natural convection flow past an infinite vertical plate is presented, wherein the plate temperature is a ramped one. The fluid considered here is a gray, absorbing/emitting but a non-scattering medium. The influence of the various parameters entering into the problem on the velocity field, temperature field, skin friction and Nusselt number is studied.
1. Introduction
The analysis of free convection flow near a vertical plate has been carried out as an important application in many industries. Numerous investigations are performed by using both analytical and numerical methods. The first exact solution of the Navier-Stokes equation was given by Stokes [1] and explains the motion of a viscous incompressible fluid past an impulsively started infinite horizontal plate in its own plane. This is known as Stokes’s first problem in the literature. If the plate is in a vertical direction and gives an impulsive motion in its own plane in a stationary fluid, then the resulting effect of buoyancy force was first studied by Sundalgekar [2] by Laplace transformation technique and the effects of heating or cooling of the plate by free convection currents were discussed. Pohlhausen [3] was among the earlier research workers, who first analyzed the steady free convective flow of a viscous, incompressible fluid past a semi-infinite vertical plate by using integral method. Later on, Ostrach [4] studied the same problem using the similarity solution method. Siegel [5] and Gebhart [6] discussed the unsteady free convective flow of a viscous incompressible fluid, bounded by a semi-infinite vertical wall by using integral and approximation methods, respectively. Several authors (cf. [7-12]) have investigated a number of unsteady free convection flows near a vertical plate under different sets of thermal conditions at the bounding plate.
Practical problems usually occupy wall conditions that are non-uniform or arbitrary. Therefore, it is very useful to investigate problems subject to step change in wall temperature. Schetz [13,14] developed an approximate analytical model for natural convection flow from a vertical plate with discontinuous wall temperature conditions. However, different techniques were attempted on this problem. Hayday et al. [10] used a numerical approach, Kelleher et al. [11] and Kao [15] used series expansions. Lee and Yovanovich [12] have attempted to improve the earlier results for step change in wall temperature.
The interaction of natural convection with thermal radiation has increased greatly during the last decade due to its importance in many practical involvements. When free convection flows occur at high temperature, radiation effects on the flow become significant. Radiation effects on the free convection flow are important in context of space technology, processes in engineering areas occur at high temperature. Soundalgekar and Takhar [16] have considered the radiative free convective flow of an optically thin gray-gas past a semi-infinite vertical plate. Radiation effects on mixed convection along an isothermal vertical plate were studied by Hossain and Takhar [17]. Raptis and Perdikis [18] studied the effects of thermal radiation and free convection flow past a moving vertical plate. Das et al. [19] have analyzed radiation effects on flow past an impulsively started infinite isothermal vertical plate by the Laplace transform technique.
Recently, Muthucumaraswamy and Janakiraman [20] studied MHD and radiation effects on moving isothermal vertical plate with variable mass diffusion. Also, Chandran et al. [8] have analyzed the unsteady natural convection flow of a viscous incompressible fluid near a vertical plate with ramped wall temperature and they have compared the results with the case of constant wall temperature. The fluid convection resulting from such a wall temperature profile is likely to be of relevance in several industrial applications, especially, where the initial temperature profiles assume importance in design processes. Saha et al. [21] investigated the natural convection boundary layer adjacent to an inclined semi-infinite flat plate subjected to ramp heating. Recently, Deka et al. [22] have analyzed the unsteady free convection flow of a viscous incompressible fluid past an infinite vertical plate with ramped wall temperature in presence of heat source.
In the present problem, it is proposed to study the effect of thermal radiation on the unsteady free convection flow of a viscous incompressible fluid past an infinite vertical plate containing a ramped type temperature profile with respect to time. Two different solutions corresponding to ramped as well as constant wall temperature, are obtained by Laplace transform technique have been shown separately.
2. Mathematical Formulation
We consider a two-dimensional flow of a viscous incompressible fluid past an infinite vertical flat plate. The fluid considered here is a gray, absorbing/emitting but a non-scattering medium. With respect to an arbitrarily chosen origin on this plate, the 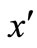 -axis is taken along the wall in the vertically upward direction, and the
-axis is taken along the wall in the vertically upward direction, and the 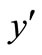 - axis is taken normal to the plate into the fluid. Initially, for time
- axis is taken normal to the plate into the fluid. Initially, for time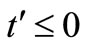 , both the fluid and the plate are at rest and assumed to be at the same temperature
, both the fluid and the plate are at rest and assumed to be at the same temperature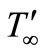 . At time
. At time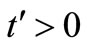 , the temperature of the plate is raised or lowered to
, the temperature of the plate is raised or lowered to 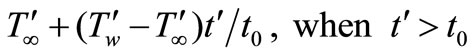 and thereafter maintained at the constant temperature
and thereafter maintained at the constant temperature 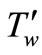 for
for .
.
We assume that the flow is laminar and is such that the effects of the convective and pressure gradient terms in the momentum equations can be neglected (see Currie et al. [23]). It is also assumed that the effect of viscous dissipation is negligible. Moreover, as the plate is infinite in extent in the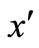 -direction, the derivatives of all the flow variables with respect to
-direction, the derivatives of all the flow variables with respect to 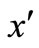 vanish and as a result of the boundary layer approximations, the physical variables are functions of
vanish and as a result of the boundary layer approximations, the physical variables are functions of 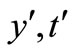 only. Thus the motion is one dimensional with only non-zero vertical velocity
only. Thus the motion is one dimensional with only non-zero vertical velocity 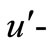 varying with
varying with  and
and  only. Due to one-dimensional nature, the equation of continuity is trivially satisfied.
only. Due to one-dimensional nature, the equation of continuity is trivially satisfied.
Then under usual Boussinesq’s approximation, the unsteady flow is governed by,
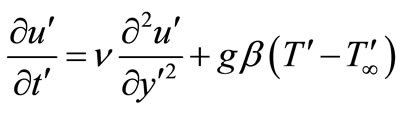 (1)
(1)
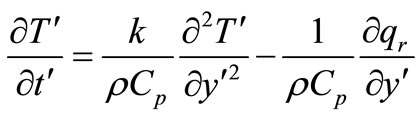 (2)
(2)
The initial and boundary conditions are,
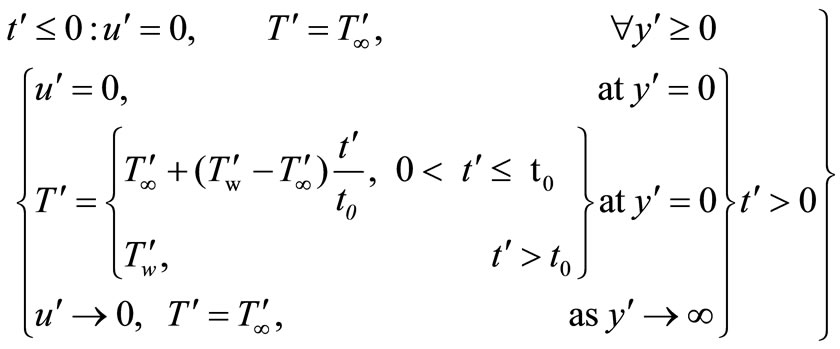 (3)
(3)
The local radiant for the case of an optically thin gray gas is expressed by,
 (4)
(4)
It is assumed that the temperature differences with the flow are sufficiently small so that 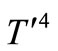 may be expressed as a linear function of the temperature, which is accomplished by expanding
may be expressed as a linear function of the temperature, which is accomplished by expanding  in a Taylor series about
in a Taylor series about 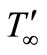 and neglecting the higher order terms. Thus,
and neglecting the higher order terms. Thus,
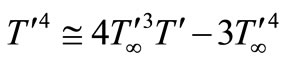 (5)
(5)
By using Equations (4) and (5), Equation (2) reduces to,
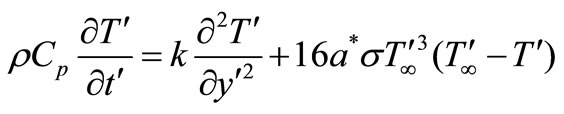 (6)
(6)
Introducing the non-dimensional quantities,
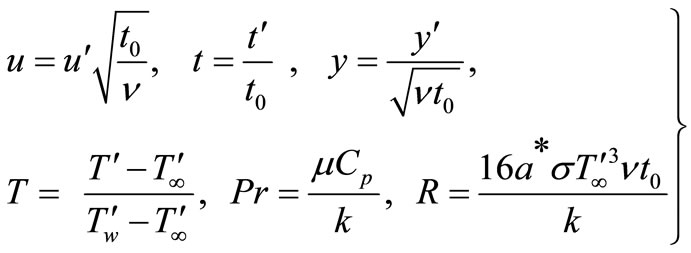 (7)
(7)
the Equations (1) and (2) reduce to,
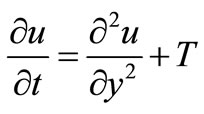 (8)
(8)
 (9)
(9)
According to the above non-dimensional process, the characteristic time t0 can be defined as,
 (10)
(10)
and then the initial and boundary conditions in non-dimensional form are,
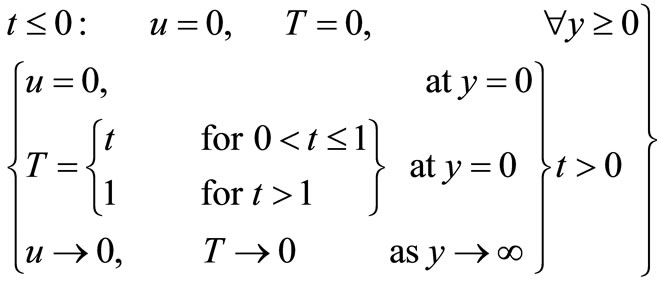 (10)
(10)
All the physical quantities are mentioned in Nomenclature.
3. Method of Solution
The Equations (8) and (9) subject to the conditions (10) are solved by the usual Laplace-transform technique and the solutions are as follows:
Case I: Pr ≠ 1
The exact solutions for temperature and velocity are given by,
 (11)
(11)
 (12)
(12)
where, (see the equation at the bottom of this page).
where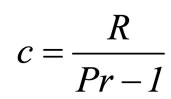 .
.
Case II: Pr = 1.
The exact solutions for temperature and velocity are,
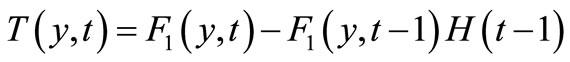 (13)
(13)
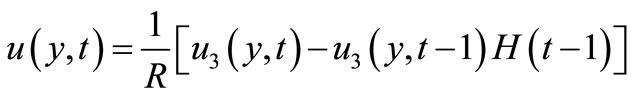 (14)
(14)
where,
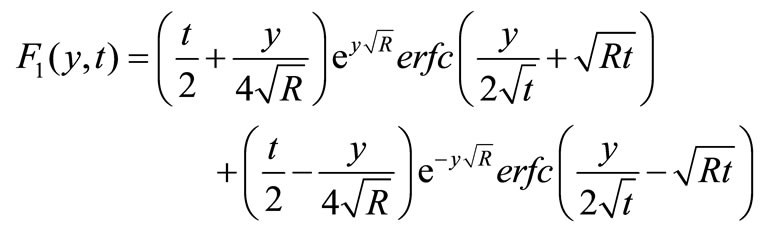

Here,  is the unit step function defined, in general as,
is the unit step function defined, in general as,

To differentiate the effect of the ramped temperature distribution from the constant wall temperature on the flow, we compare both solutions obtained. The solutions for temperature and velocity for the flow near an isothermal stationary plate can be obtained as,
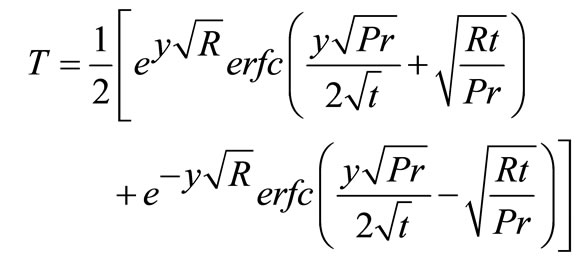 (15)
(15)
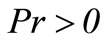
 (16)
(16)
![]()
![]()
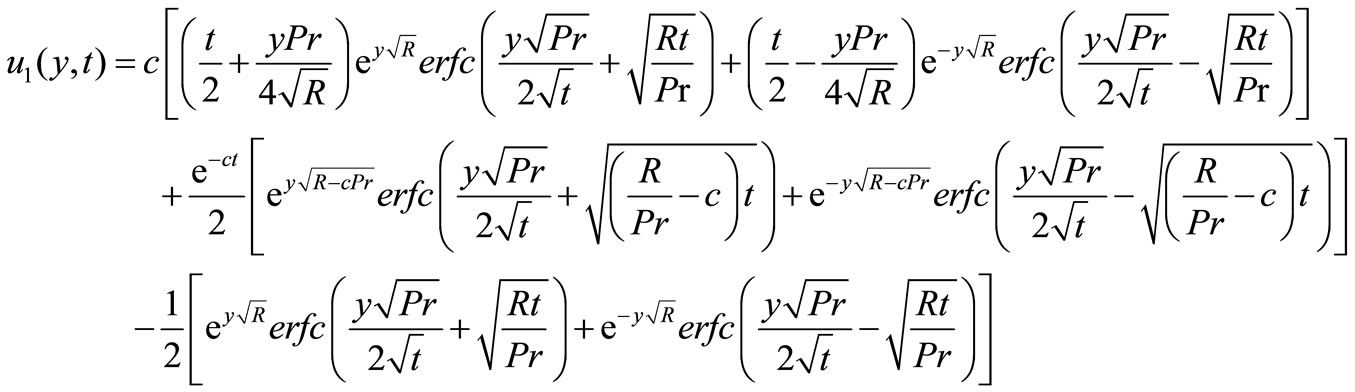

where,
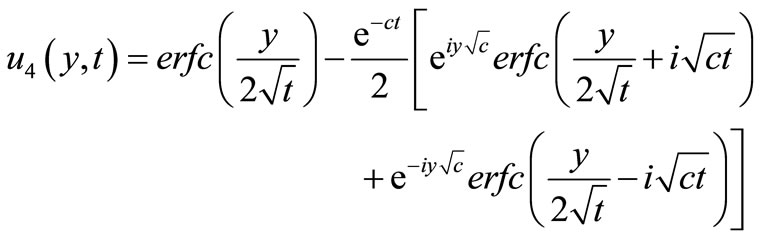
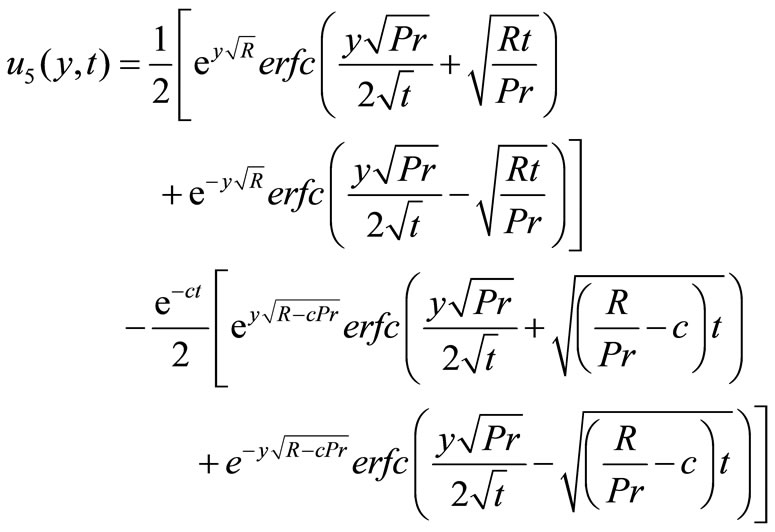
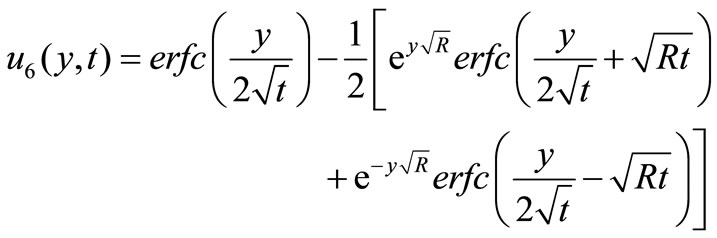
4. Nusselt Number and Skin-Friction
We now study the heat transfer coefficient, i.e. Nusselt number, which is given in non-dimensional form by,

where,
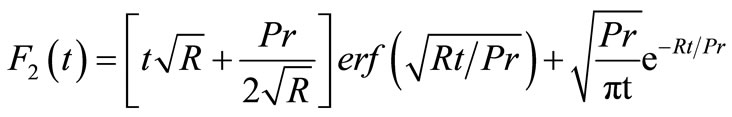
while, for the isothermal plate,
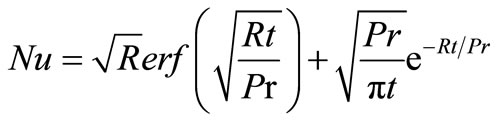
From the velocity field, we now study the skin friction. The non-dimensional form of skin-friction is given by,

where,
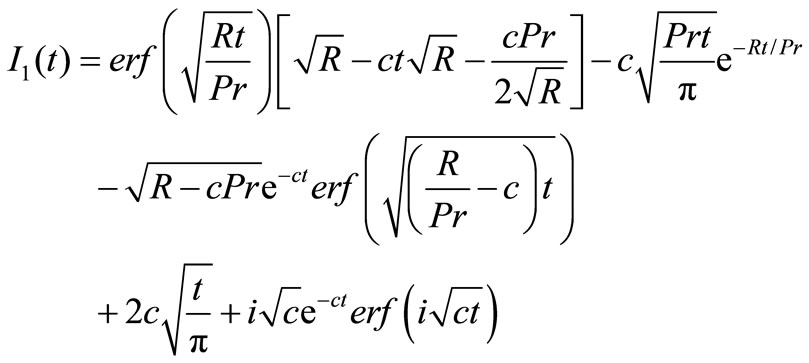
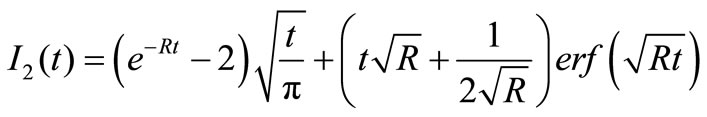
Again, the skin friction for isothermal plate is given by,
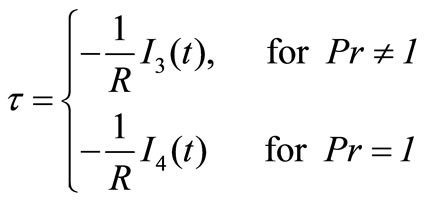
where,
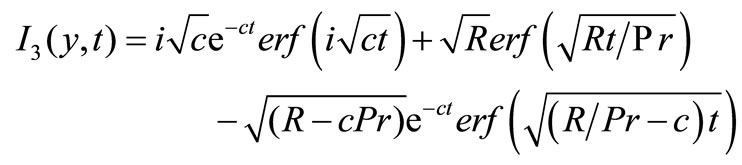
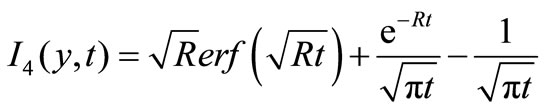
5. Results and Discussions
In order to understand the effects of different physical parameters, namely;  (Prandtl number),
(Prandtl number), 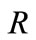 (radiation parameter) and
(radiation parameter) and 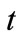 (time), on the nature of the flow, computations are carried out for velocity, temperature, Nusselt number and skin friction. The computed results are presented graphically. In all the figures, dotted lines correspond to solutions without ramped wall temperature.
(time), on the nature of the flow, computations are carried out for velocity, temperature, Nusselt number and skin friction. The computed results are presented graphically. In all the figures, dotted lines correspond to solutions without ramped wall temperature.
Figures 1-3 display the effect of 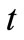 (time) on the temperature field for the case of air (Pr = 0.71). It is observed that temperature increases with an increase in
(time) on the temperature field for the case of air (Pr = 0.71). It is observed that temperature increases with an increase in 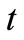 (time). It is also found that the temperature decreases with
(time). It is also found that the temperature decreases with  from its ramped value on the plate to its free stream value for all values of time
from its ramped value on the plate to its free stream value for all values of time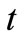 .
.
Figure 2 represents the temperature profiles for different values of 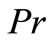 at
at 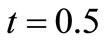 and
and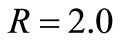 . It is found that the temperature decreases with an increase in
. It is found that the temperature decreases with an increase in . Figure 3 shows the effect of radiation parameter R on the temperature field for fixed values of
. Figure 3 shows the effect of radiation parameter R on the temperature field for fixed values of  and
and 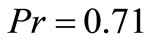 and demonstrates that the temperature decreases gradually with increasing values of
and demonstrates that the temperature decreases gradually with increasing values of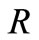 .
.
From Figures 1-3 we have presented the temperature variation with the two types of boundary conditions,
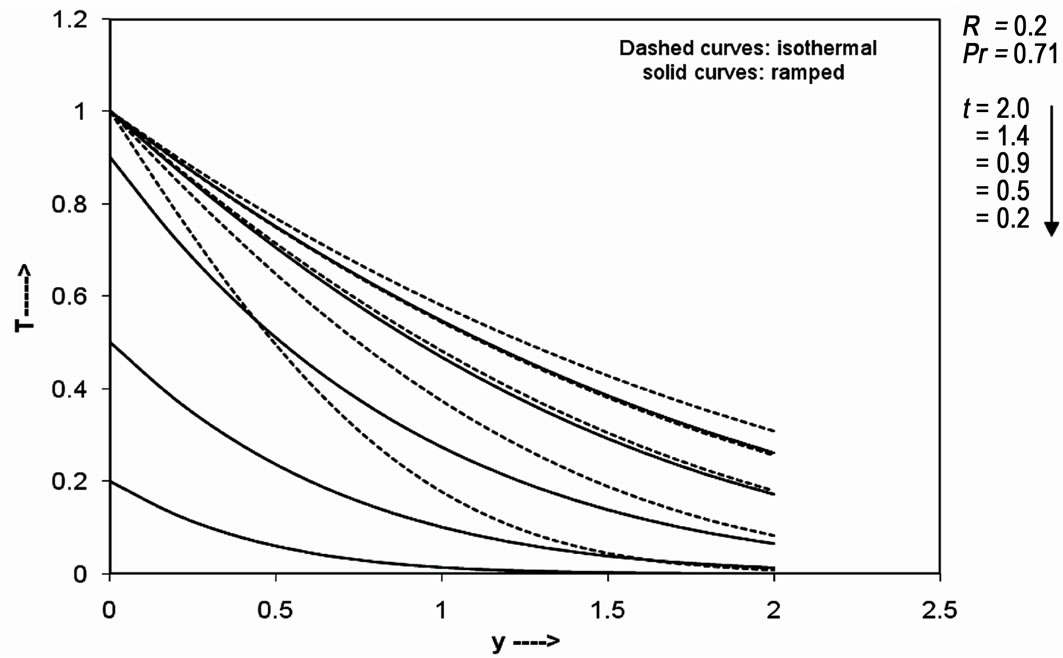
Figure 1. Temperature profile for different time t.

Figure 2. Temperature profile for different Pr.
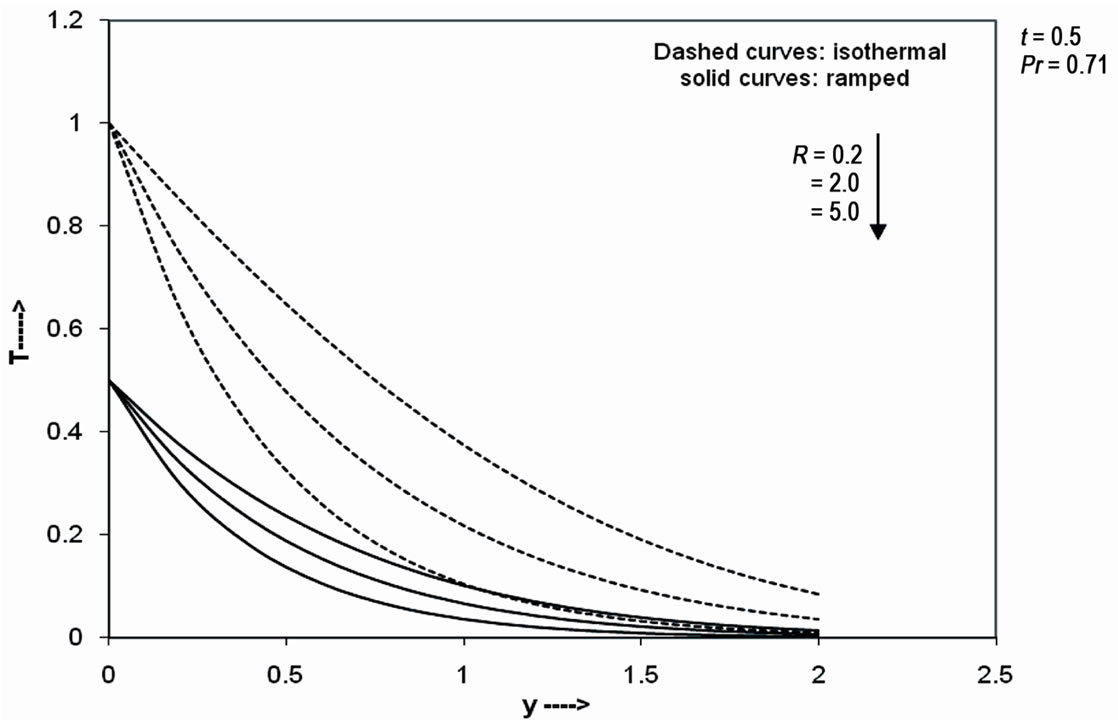
Figure 3. Temperature profile for different R.
ramped and constant plate temperature. We observe that the fluid temperature is greater in the case of isothermal plate than in the case of ramped temperature at the plate. This should be expected since in the latter case, the heating of the fluid takes place more gradually than in the isothermal case. Also, we observe that the temperature is maximum near the plate and decreases away from the plate and finally takes free stream value for all values of ,
, 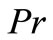 and
and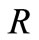 .
.
In Figures 4 and 5, the velocity profiles are shown for different values of physical parameters involved. Figure 4 reveals velocity variations with 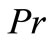 and
and 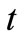 at
at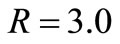 . It demonstrates that the velocity decreases with increaseing the Prandtl number. Figure 5 illustrates the influence of
. It demonstrates that the velocity decreases with increaseing the Prandtl number. Figure 5 illustrates the influence of  on the velocity field for both ramped temperature and isothermal plate. It is observed that the fluid velocity decreases on increasing radiation parameter
on the velocity field for both ramped temperature and isothermal plate. It is observed that the fluid velocity decreases on increasing radiation parameter  in the boundary layer region. This implies that the radiation decelerates fluid velocity for both ramped temperature and isothermal plate. Figures 4 and 5 also demonstrate that the velocity increases with an increase in time
in the boundary layer region. This implies that the radiation decelerates fluid velocity for both ramped temperature and isothermal plate. Figures 4 and 5 also demonstrate that the velocity increases with an increase in time . Again, from Figures 4 and 5, we observe that the velocity increases with
. Again, from Figures 4 and 5, we observe that the velocity increases with  near the plate, becomes maximum and then decreases away from the plate and finally takes asymptotic value for all values of
near the plate, becomes maximum and then decreases away from the plate and finally takes asymptotic value for all values of . Lastly, it is seen that the velocity in case of ramped temperature plate is always less than the flow induced by a plate of constant temperature.
. Lastly, it is seen that the velocity in case of ramped temperature plate is always less than the flow induced by a plate of constant temperature.
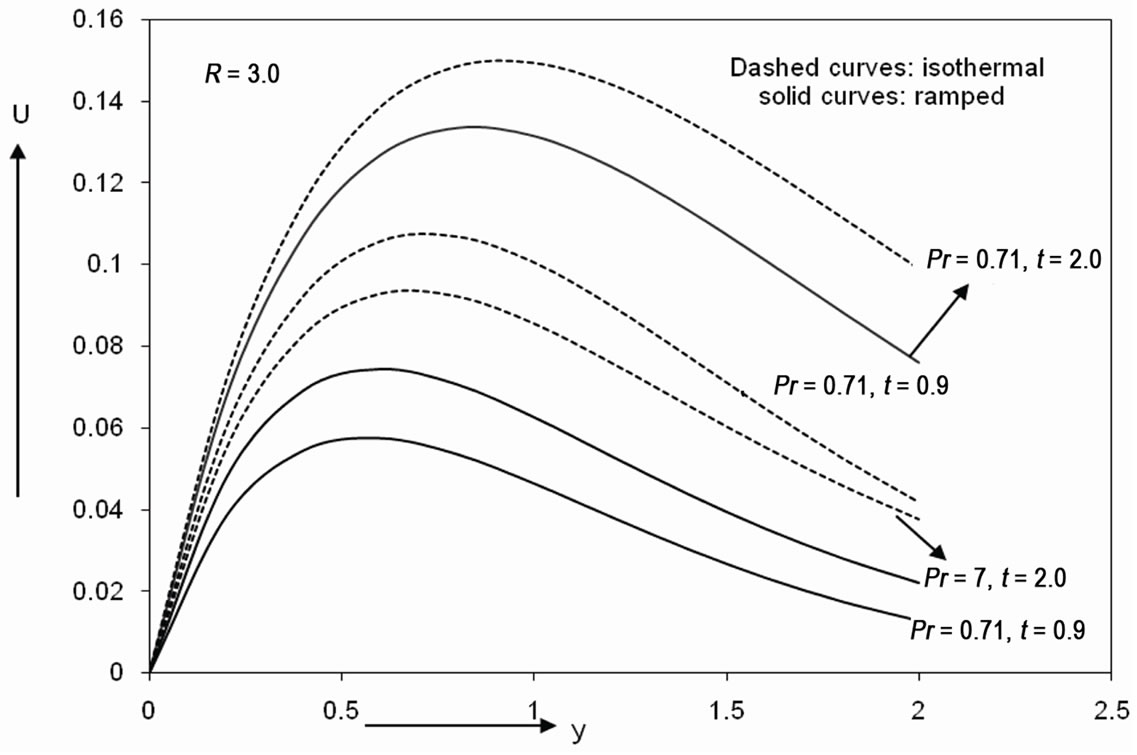
Figure 4. Velocity profile for different Pr and t.
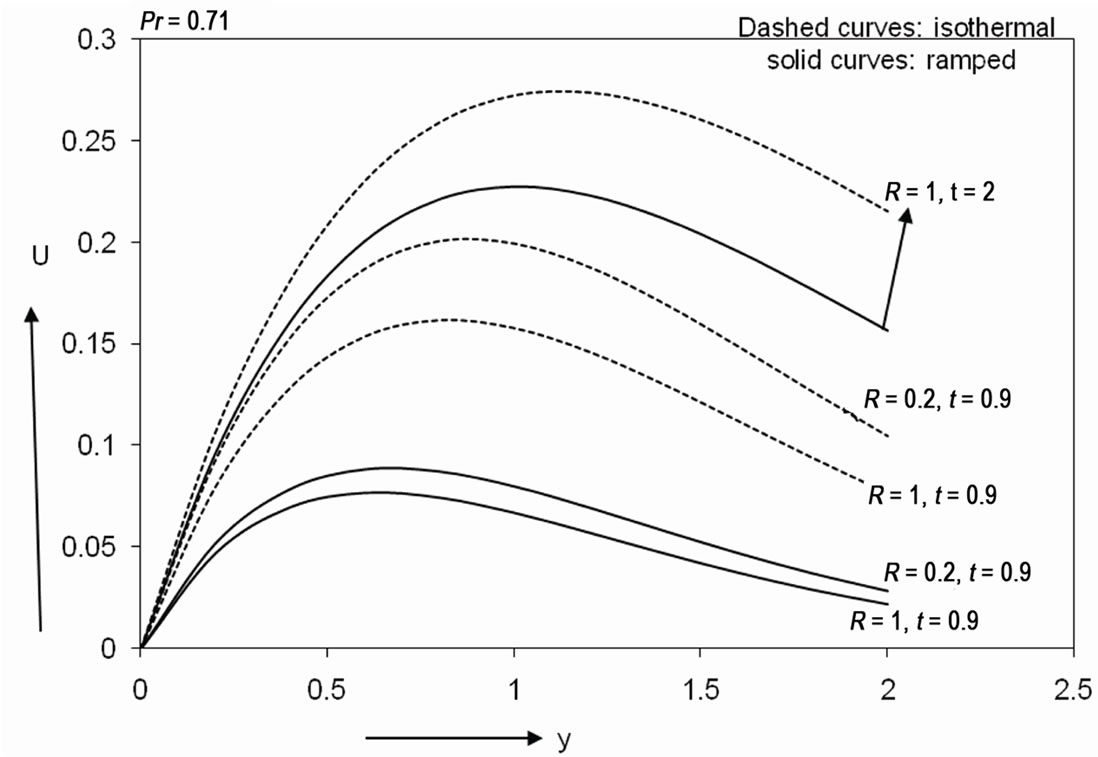
Figure 5. Velocity profile for different R and t.
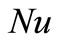 is calculated for different
is calculated for different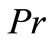 ,
, 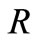 and
and  and presented in Figures 6 and 7. It is clear from the figures that for the ramped plate temperature, the Nusselt number increases for a range
and presented in Figures 6 and 7. It is clear from the figures that for the ramped plate temperature, the Nusselt number increases for a range 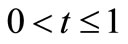 and decreases for
and decreases for 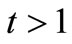 for all
for all 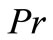 and
and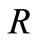 . But in case of constant wall temperature, the Nusselt number decreases with respect to
. But in case of constant wall temperature, the Nusselt number decreases with respect to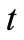 .
.
The numerical values of t are evaluated for different values of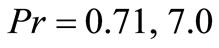 ;
;  and depicted in Figure 8 The effects of ramped and constant wall temperature on skin friction are also presented in this figure. We have seen that due to the presence of radiation, the skin-friction is greater in case of ramped temperature of the plate than the case of an isothermal plate. It is also noticed that for small values of t < 1, there is a quick fall in the skin friction in the case of ramped temperature of the plate, whereas the skin friction decreases more gradually with time for the case of isothermal plate. Further, we observe that the skin friction co-efficient increases with
and depicted in Figure 8 The effects of ramped and constant wall temperature on skin friction are also presented in this figure. We have seen that due to the presence of radiation, the skin-friction is greater in case of ramped temperature of the plate than the case of an isothermal plate. It is also noticed that for small values of t < 1, there is a quick fall in the skin friction in the case of ramped temperature of the plate, whereas the skin friction decreases more gradually with time for the case of isothermal plate. Further, we observe that the skin friction co-efficient increases with 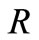 for both ramped temperature and isothermal plate, which illustrates that radiation has tendency to enhance the skin friction. It is also observed that the skin friction is enhanced with
for both ramped temperature and isothermal plate, which illustrates that radiation has tendency to enhance the skin friction. It is also observed that the skin friction is enhanced with . Lastly, we find that the ber.perayure skin-friction is more in water as compared to that in air.
. Lastly, we find that the ber.perayure skin-friction is more in water as compared to that in air.
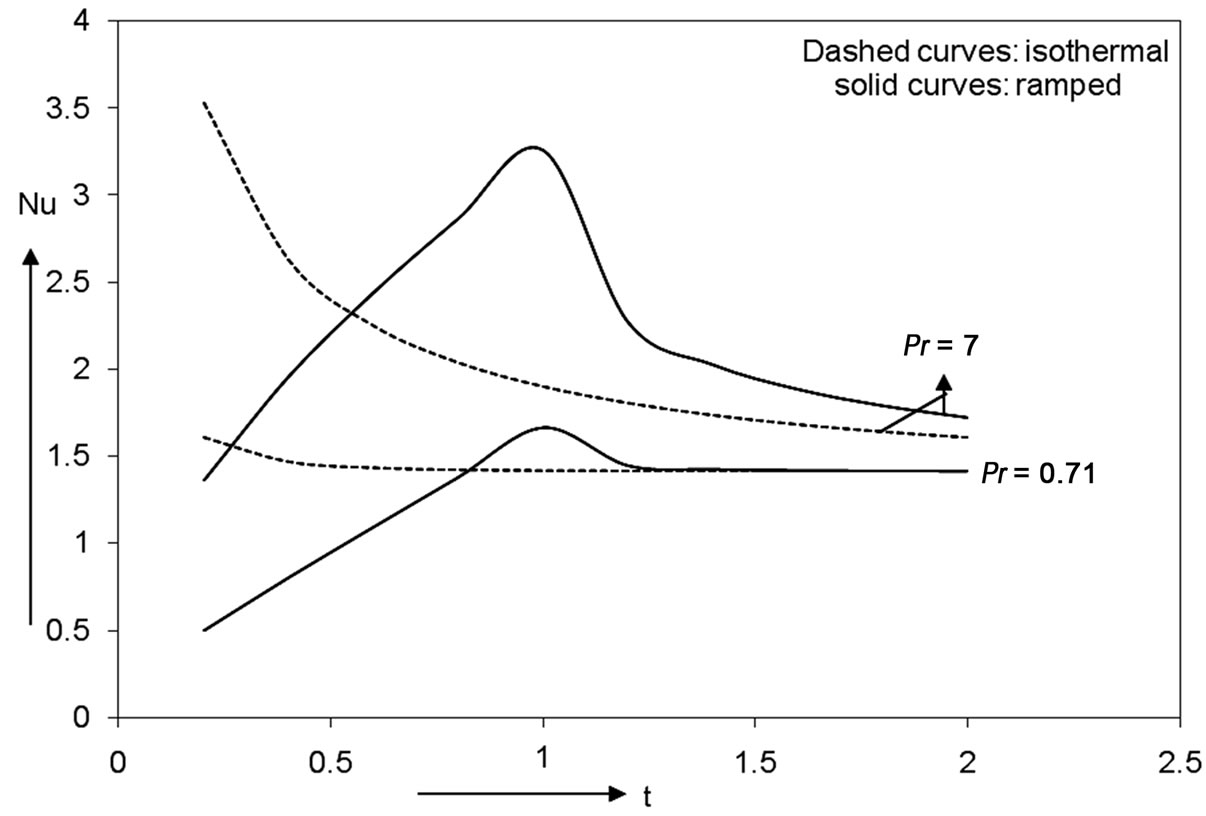
Figure 6. Variation of Nusselt number when R = 2.
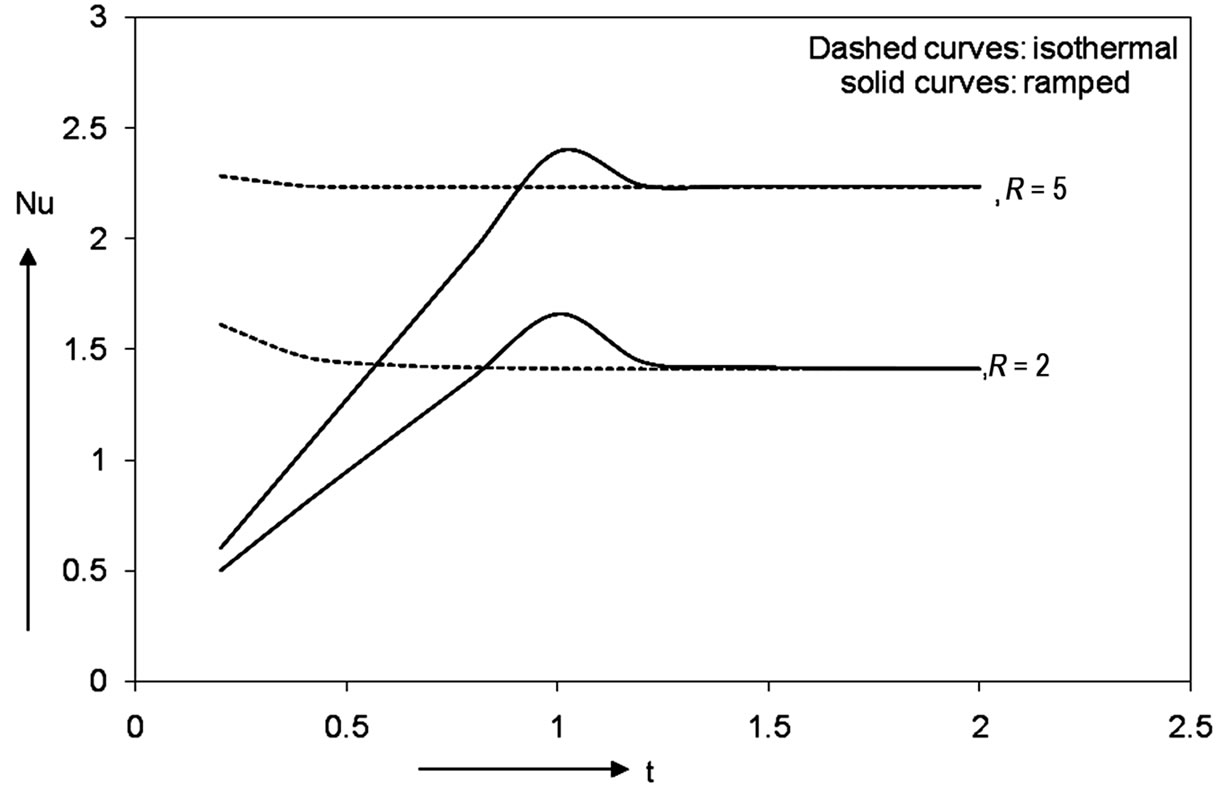
Figure 7. Variation of Nusselt number when Pr = 0.71.

Figure 8. Variation of skin friction for ramped and isothermal temperature.
6. Conclusions
An analysis is performed to study the effect of radiation on unsteady free convection flow past an infinite vertical plate with ramped wall temperature. The non-dimensional forms of the governing equations of the fluid flow are solved by Laplace-transform technique. The solutions for velocity, temperature are studied graphically. Also, the Nusselt number and skin friction have been discu-ssed.
Following observations are made from the study:
1) Temperature of the fluid increases with an increase in time 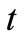 but as
but as 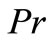 increases, temperature decreases. Also, the temperature decreases gradually with
increases, temperature decreases. Also, the temperature decreases gradually with .
.
2) The temperature decreases with 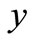 from its ramped value on the plate to its free stream value.
from its ramped value on the plate to its free stream value.
3) The presence of radiation tends to decelerate the fluid flow for both ramped temperature and isothermal plate. Also, fluid velocity accelerates as time progresses.
4) The velocity decreases with increasing the Prandtl number.
5) Nusselt number increases for 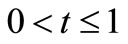 and decreases for
and decreases for  for all
for all 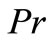 and
and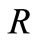 .
.
6) Skin friction increases with increasing  and
and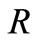 .
.
7. REFERENCES
- G. G. Stokes, “On the Effect of Internal Friction of Fluids on the Motion of Pendulums,” Mathematical and Physical Papers, Vol. 3, 1851, pp. 8-106.
- V. M. Soundalgekar, “Free Convection Effects on Stokes’s Problem for a Vertical Plate,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 99C, No. 3, 1977, pp. 499-501. doi:10.1115/1.3450729
- E. Pohlhausen, “Der Wareastausch Zwischen Festen Korpenn und Flussigkeiten mit Kleineer Reibung und Kleinerwarmeletung,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 1, No. 2, 1921, pp. 115-121. doi:10.1002/zamm.19210010205
- S. Ostrach, “An Analysis of Laminar Free Convection Flow Heat Transfer about a Flat Plate Parallel to the Direction of the Generating Body Force,” NASA Report No. 1111, 1953.
- R. Siegel, “Transient Free Convection from a Vertical Flat Plate,” Transactions of the American Society of Mechanical Engineers, Vol. 80, 1958, pp. 347-359.
- B. Gebhart, “Transient Natural Convection from Vertical Elements,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 83C, 1961, pp. 61-67.
- P. Chandran, N. C. Sacheti and A. K. Singh, “Exact Solutions for the Convective Flow of Fluids of Different Prandtl Numbers Near an Infinite Vertical Plate in a Rotating System,” International Journal of Applied Mechanics and Engineering, Vol. 6, No. 3, 2001, pp. 573- 590.
- P. Chandran, N. C. Sacheti and A. K. Singh, “Natural Convection Near a Vertical Plate with Ramped Wall Temperature,” Heat and Mass Transfer, Vol. 41, No. 5, 2005, pp. 459-464. doi:10.1007/s00231-004-0568-7
- P. Ganesan and G. Palani, “Natural Convection Effects on Impulsively Started Inclined Plate with Heat and Mass Transfer,” Heat Mass Transfer, Vol. 39, 2003, pp. 277-283.
- A. A. Hayday, D. A. Bowlus and R. A. McGraw, “Free Convection from a Vertical Flat Plate with Step Discontinuities in Surface Temperature,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 89, No. 3, 1967, pp. 244-250.
- M. Kelleher, “Free Convection from a Vertical Plate with Discontinuous Wall Temperature,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 93, 1971, 349-356.
- S. Lee and M. M. Yovanovich, “Laminar Natural Convection from a Vertical Plate with a Step Change in Wall Temperature,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 113, 1991, pp. 501- 504.
- J. A. Schetz, “On the Approximate Solution of Viscous- flow Problems,” Journal of Applied Mechanics, Vol. 30, No. 2, 1963, pp. 263-268. doi:10.1115/1.3636522
- J. A. Schetz and R. Eichhorn, “Unsteady Natural Convection in the Vicinity of a Doubly Infinite Vertical Plate,” American Society of Mechanical Engineers Journal of Heat Transfer, Vol. 84, 1962, pp. 334-338.
- T. T. Kao, “Laminar Free Convective Heat Transfer Response along a Vertical Flat Plate with Step Jump in Surface Temperature,” Letters in Heat and Mass Transfer, Vol. 2, No. 5, 1975, pp. 419-428. doi:10.1016/0094-4548(75)90008-9
- V. M. Soundalgekar and H. S. Takhar, “Radiation Effects on Free Convection Flow Past a Semi-Infinite Vertical Plate,” Modeling Measurement and Control, Vol. B51, 1993, pp. 31-40.
- M. A. Hossain and H. S. Takhar, “Radiation Effects on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- A. Raptis and C. Perdikis, “Radiation and Free Convection Flow Past a Moving Plate,” International Journal of Applied Mechanics and Engineering, Vol. 4, No. 4, 1999, pp. 817-821.
- U. N. Das, R. K. Deka and V. M. Soundalgekar, “Radiation Effects on Flow Past an Impulsively Started Vertical Infinite Plate,” Journal of Theoretical and Applied Mechanics, Vol. 1, 1996, pp. 111-115.
- R. Muthucumaraswamy and B. Janakiraman, “MHD and Radiation Effects on Moving Isothermal Vertical Plate with Variable Mass Diffusion,” Journal of Theoretical and Applied Mechanics, Vol. 33, No. 1, 2006, pp. 17-29. doi:10.2298/TAM0601017M
- S. C. Saha, C. Lei and J. C. Patterson, “On the Natural Convection Boundary Layer Adjacent to an Inclined Flat Plate Subject to Ramp Heating,” Proceedings of 16th Australian Fluid Mechanics Conference, Crown Plaza, Gold Coast, 11-16 September 2007, pp. 121-124.
- D. Deka and R. K. Deka, “Natural Convection near a Vertical Plate with Ramped Wall Temperature and Heat Source,” Far East Journal of Applied Mathematics, Vol. 1, No. 41, 2010, pp. 21-32.
- I. G. Currie, “Fundamental Mechanics of Fluids,” 3rd Edition, Marce-Dekker, New York, 2003.



