Engineering
Vol. 3 No. 7 (2011) , Article ID: 6233 , 10 pages DOI:10.4236/eng.2011.37087
Boundary Layer Flow of an Unsteady Dusty Fluid and Heat Transfer over a Stretching Sheet with Non-uniform Heat Source/Sink
Department of Studies and Research in Mathematics, Kuvempu University,
Shimoga, India
E-mail: bjgireesu@rediffmail.com
Received March 28, 2011; revised April 27, 2011; accepted May 10, 2011
Keywords: Unsteady Flow, Heat Transfer, Boundary Layer Flow, Stretching Surface, Dusty Fluid, Fluid-Particle Interaction Parameter and Non-uniform Heat Source/Sink
ABSTRACT
An analysis has been carried out to study the effect of hydrodynamic laminar boundary layer flow and heat transfer of a dusty fluid over an unsteady stretching surface in the presence of non-uniform heat source/sink. Heat transfer characteristics are examined for two different kinds of boundary conditions, namely 1) variable wall temperature and 2) variable heat flux. The governing partial differential equations are transformed to system of ordinary differential equations. These equations are solved numerically by applying RKF-45 method. The effects of various physical parameters such as magnetic parameter, dust interaction parameter, number density, Prandtl number, Eckert number, heat source/sink parameter and unsteadiness parameter on velocity and temperature profiles are studied.
1. Introduction
The momentum and heat transfer in the laminar boundary layer flow on a continuous moving surface are important from theoretical as well as practical points of view because of their wide range of applications in polymer technology and industrial manufacturing process. Some examples are in the extrusion of a polymer in a melt-spinning process, metals and plastics, cooling of an infinite metallic plate in a cooling bath, the boundary layer along material handling conveyers, the aerodynamic extrusion of plastic sheets, the boundary layer along a liquid film in condensation processes, glass blowing, the cooling and/or drying of papers, drawing plastic films, continuous casting and spinning of fibers. In these cases the quality of the final product depends on the rate of heat transfer at the stretching surface.
In view of these applications, Sakiadis [1] initiated the study of the boundary layer flow over a stretched surface moving with a constant velocity and formulated a boundary-layer equation for two-dimensional and axisymmetric flows. The temperature field in the flow over a linearly stretching surface subject to a uniform unit flux was studied by Grubka and Bobba [2]. The two-dimensional steady flow of an incompressible viscous fluid caused by a linearly stretching plate was first discussed by Crane [3]. Vajravelu and Nayfeh [4] discussed the analysis of hydromagnetic flow of a dusty fluid over a stretching sheet. The effects of buoyancy force on the development of velocity and thermal boundary layer flows over a stretching sheet has been initiated by Chen [5].
Moreover Abel, Siddeshwar and Mahantesh [6] have obtained the solution of heat transfer in a viscoelastic boundary layer flow over a stretching sheet in the presence of viscous dissipation and non-uniform heat source. The problem of mixed convection adjacent to a vertical, continuously stretching sheet in the presence of a variable magnetic field has been studied by Ishak, Nazar and Pop [7]. Aziz [8] obtained the numerical solution for laminar thermal boundary over a flat plate with a convective surface boundary condition using the symbolic algebra software Maple. Elbashbeshy and Bazid [9] investigated on heat transfer in a porous medium over a stretching sheet with internal generation and suction or injection. The unsteady heat transfer problems over a stretching surface, which is stretched with a velocity that depends on time are considered by Andersson, Aareseth and Dandapat [10], a new similarity solution for the temperature field is devised, which transforms the timedependent thermal energy equation to an ordinary differential equation.
Further, Elbashbeshy and Bazid [11] studied the heat transfer over an unsteady stretching surface. Sharidan Mahmood and Pop [12] considered the similarity solutions for the unsteady boundary layer flow and heat transfer over a stretching sheet for special distributions of the stretching velocity and surface temperature. Tsai, Huang and Huang [13] presented a similarity solution for flow and heat transfer over an unsteady stretching surface with a non-uniform heat source. Recently Ishak, Nazar and Pop [14] have also investigated the unsteady laminar boundary layer over a continuously stretching permeable surface. Swati and Andersson [15] proposed a effect of slip flow and heat transfer analysis over an unsteady stretching surface. Dulal and Hiremath [16] determined the heat transfer characteristics in the laminar boundary layer flow over an unsteady stretching sheet which is placed in a porous medium in the presence of viscous dissipation and internal absorption or generation.
In the light of this, the purpose of this article is to study the effect of magnetic field on unsteady boundary layer flow and heat transfer of a dusty fluid over a stretching sheet in the presence of non-uniform heat source/sink. The temperature distribution is carried out with Variable Wall Temperature (VWT) and Variable Heat Flux (VHF) temperature boundary conditions. Highly non-linear momentum and heat transfer equations are solved numerically using Runge-Kutta-Fehlberg-45 method with the help of Maple software. Further the effect of various physical parameters like Hartmann number, dust interaction parameter, number density, Prandtl number, Eckert number, heat source/sink parameter and unsteadiness parameter on velocity fields and temperature are analyzed.
2. Mathematical Formulation and Solution of the Problem
Consider an unsteady two-dimensional laminar boundary layer flow and heat transfer of an incompressible viscous dusty fluid past a semi-infinite stretching sheet coinciding with the plane , then the fluid is occupied above the sheet
, then the fluid is occupied above the sheet . Keeping the origin fixed, two equal and opposite forces are suddenly applied along the x-axis, which results in stretching of the sheet and hence, flow is generated. The continuous sheet moves in its own plane with a velocity
. Keeping the origin fixed, two equal and opposite forces are suddenly applied along the x-axis, which results in stretching of the sheet and hence, flow is generated. The continuous sheet moves in its own plane with a velocity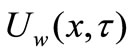 . At the same time, the wall temperature
. At the same time, the wall temperature 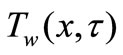 of the sheet is suddenly raised from
of the sheet is suddenly raised from  to
to 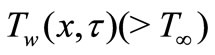 or there is suddenly imposed a heat flux
or there is suddenly imposed a heat flux 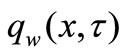 at the wall. Under these assumptions, the governing basic equations in the usual notation can be written as
at the wall. Under these assumptions, the governing basic equations in the usual notation can be written as
 (1)
(1)
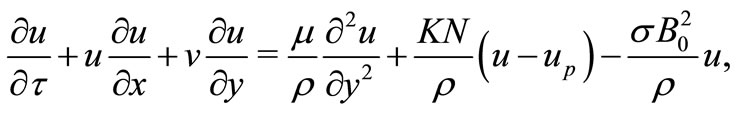 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
where 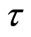 is the time,
is the time, 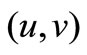 and
and  denote the velocity components of the fluid and particle phase along the x-axes and y-axes respectively.
denote the velocity components of the fluid and particle phase along the x-axes and y-axes respectively. 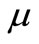 is the coefficient of viscosity of fluid,
is the coefficient of viscosity of fluid, 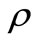 and
and  are the density of the fluid and particle phase,
are the density of the fluid and particle phase,  is the induced magnetic field and
is the induced magnetic field and 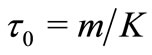 is the relaxation time of particle phase, N is the number density of the particle phase, K the Stoke’s resistance co-efficient (for spherical particles of radius r is
is the relaxation time of particle phase, N is the number density of the particle phase, K the Stoke’s resistance co-efficient (for spherical particles of radius r is ), m is the mass concentration of dust particles. In deriving these equations, the Stokesian drag force is considered for the interaction between the fluid and particle phase and the induced magnetic field is neglected. Also it is assumed that the external electric field to be zero and the electric field as a result of polarization of charges is negligible.
), m is the mass concentration of dust particles. In deriving these equations, the Stokesian drag force is considered for the interaction between the fluid and particle phase and the induced magnetic field is neglected. Also it is assumed that the external electric field to be zero and the electric field as a result of polarization of charges is negligible.
The appropriate boundary conditions for the above described flow are given by
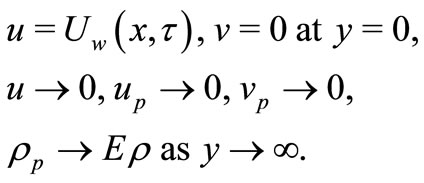 (6)
(6)
where 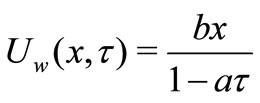 is the sheet velocity,
is the sheet velocity, 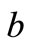 is the initial stretching rate being a positive constant,
is the initial stretching rate being a positive constant, 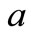 is positive constant which measures the unsteadiness, whereas the effective stretching rate
is positive constant which measures the unsteadiness, whereas the effective stretching rate  is increasing with time. In the context of polymer extrusion the material properties and in particular the elasticity of the extruded sheet may vary with time even though the sheet is being pulled by a constant force. With unsteady stretching (i.e.
is increasing with time. In the context of polymer extrusion the material properties and in particular the elasticity of the extruded sheet may vary with time even though the sheet is being pulled by a constant force. With unsteady stretching (i.e.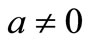 ), however,
), however,  becomes the representative time scale of the resulting unsteady boundary layer problem and E is the density ratio.
becomes the representative time scale of the resulting unsteady boundary layer problem and E is the density ratio.
The mathematical analysis of the problem is simplified by introducing the following dimensionless coordinates in terms of similarity variable 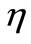 (see Dulal and Hiremath [16]) and the similarity function
(see Dulal and Hiremath [16]) and the similarity function 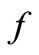 as
as
 (7)
(7)
where a prime denotes the differentiation with respect to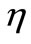 .
.
Using the relations (8), the governing Equations (1)- (5) reduces to
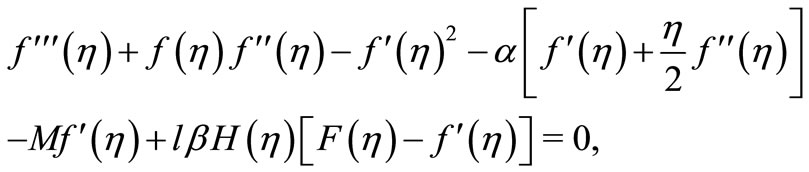 (8)
(8)
 (9)
(9)
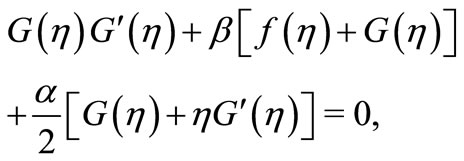 (10)
(10)
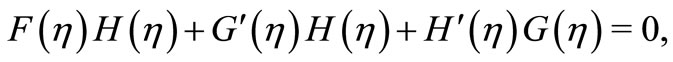 (11)
(11)
where the parameter that measures the unsteadiness is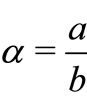 ,
,  is the relative density,
is the relative density,  is the magnetic field parameter,
is the magnetic field parameter, 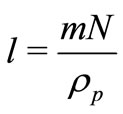 is the mass concentration,
is the mass concentration, 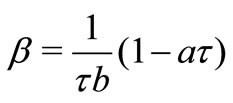 is the fluid-particle interaction parameter.
is the fluid-particle interaction parameter.
The boundary conditions are transformed to:
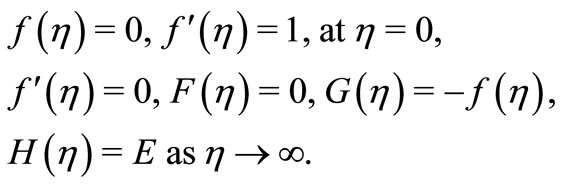 (12)
(12)
3. Heat Transfer Analysis
The governing unsteady, dusty boundary layer heat transport equations in the presence of temperature dependent internal heat generation/absorption for two-dimensional flow are [17]
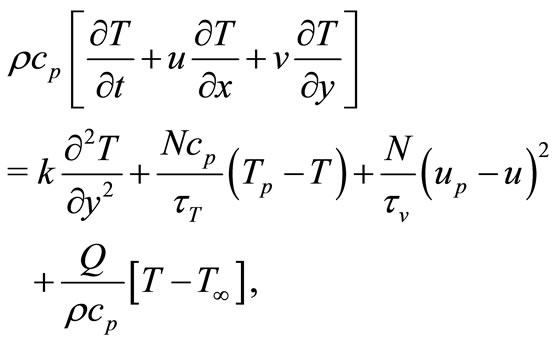 (13)
(13)
 (14)
(14)
where T and 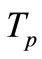 is the temperature of the fluid and dust particle,
is the temperature of the fluid and dust particle, 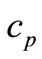 and
and  are the specific heat of fluid and dust particles,
are the specific heat of fluid and dust particles,  is the Thermal equilibrium time and is time required by the dust cloud to adjust its temperature to the fluid,
is the Thermal equilibrium time and is time required by the dust cloud to adjust its temperature to the fluid,  is the thermal conductivity,
is the thermal conductivity, 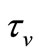 is the relaxation time of the of dust particle i.e., the time required by a dust particle to adjust its velocity relative to the fluid. The term
is the relaxation time of the of dust particle i.e., the time required by a dust particle to adjust its velocity relative to the fluid. The term 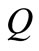 represents the heat source when
represents the heat source when 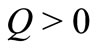 and sink when
and sink when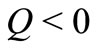 .
.
To solve the temperature Equations (13) and (14), we consider two general cases of temperature boundary conditions, namely 1) Boundary with variable wall temperature (VWT) and 2) Boundary with variable heat flux (VHF).
Case 1: Variable Wall Temperature (VWT)
For this heating process, we employ the following variable wall temperature boundary conditions:
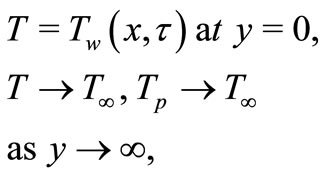 (15)
(15)
where  is the surface temperature of the sheet varies with the distance
is the surface temperature of the sheet varies with the distance 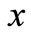 from the slot and time
from the slot and time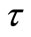 ,
,  is a reference temperature such that
is a reference temperature such that  and
and  is the temperature far away from the stretching surface with
is the temperature far away from the stretching surface with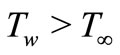 .
.
We now introduce the dimensionless variables for the temperatures 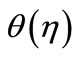 and
and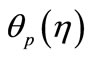 , as follows:
, as follows:
 (16)
(16)
where .
.
By using the similarity variable 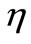 and (16) into (13) and (14), one can arrive the following dimensionless system of equations:
and (16) into (13) and (14), one can arrive the following dimensionless system of equations:
 (17)
(17)
 (18)
(18)
where  is Prandtl number,
is Prandtl number,  is the Eckret number,
is the Eckret number, 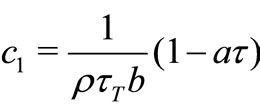 and
and  are the local fluid-particle interaction parameters for temperature,
are the local fluid-particle interaction parameters for temperature,  is the local fluid-particle interaction parameter of velocity,
is the local fluid-particle interaction parameter of velocity,  is the source sink parameter,
is the source sink parameter, 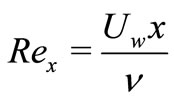 is the local Reynold’s number and
is the local Reynold’s number and .
.
Corresponding thermal boundary conditions are given by
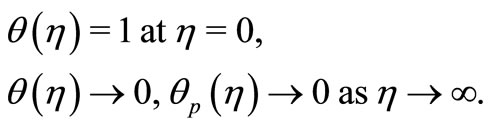 (19)
(19)
Case 2: Variable Heat Flux (VHF)
In VHF case, define the following boundary conditions on temperature:
 (20)
(20)
where .
.
In order to obtain similarity solution for temperature, we define dimensionless temperature variables in VHF case as follows
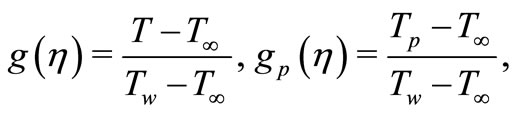
where as .
.
With this dimensional energy Equations (13) and (14) takes the following non-dimensional form
 (21)
(21)
 (22)
(22)
where Eckert number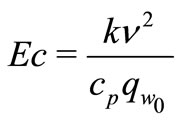 . The non-dimensional form of boundary conditions (20) are written as
. The non-dimensional form of boundary conditions (20) are written as
 (23)
(23)
The physical quantities of interest are the skin friction coefficient 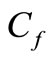 and the local Nusselt number
and the local Nusselt number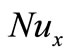 , which are defined as
, which are defined as

where the surface shear stress 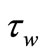 and the surface heat flux
and the surface heat flux  are given by
are given by

Using the non-dimensional variables, we obtain
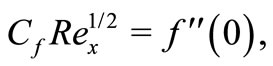
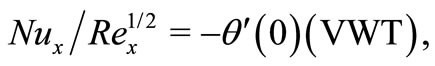

4. Numerical Solution
The Equations (8)-(11), (17)-(18) (VWT case) or (21)-(22) (VHF case) are highly non-linear, ordinary differential equations. These equations with the boundary conditions (12), (19) and (23) will constitute a boundary value problem. In order to solve these equations numerically we follow the most efficient numerical technique with fourth-fifth Runge Kutta Fehlberg scheme with the help of Maple software [8]. In this method it is most important to choose a appropriate finite values of  (here we take
(here we take ). In order to check the accuracy of the numerical solution procedure used, a comparison of heat transfer characteristics at the wall for
). In order to check the accuracy of the numerical solution procedure used, a comparison of heat transfer characteristics at the wall for 
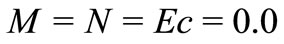 for different values of
for different values of  in the absence of internal heat generation/absorption and results are tabulated in Table 1. From this table we note that there is a close agreement with these approaches and thus verifies the accuracy of the method used.
in the absence of internal heat generation/absorption and results are tabulated in Table 1. From this table we note that there is a close agreement with these approaches and thus verifies the accuracy of the method used.
5. Results and Discussion
In the present paper, we investigate the hydromagnetic boundary layer flow and heat transfer of a dusty fluid over a stretching sheet in presence of internal heat generation or absorption. Similarity transformations are used to convert the governing time dependent non-linear boundary layer equations into a system of non-linear ordinary differential equations. Numerical solutions are presented for highly non-linear boundary layer equations. The temperature profiles for  and
and 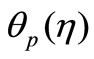 in VWT case and
in VWT case and  and
and 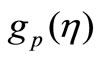 in VHF case depicted graphically. The computations have been carried out to study the effect of various governing parameters such as magnetic parameter (
in VHF case depicted graphically. The computations have been carried out to study the effect of various governing parameters such as magnetic parameter ( ), number density (
), number density ( ), fluid particle interaction parameter (
), fluid particle interaction parameter ( ), heat source or sink parameter (
), heat source or sink parameter (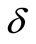 ), Prandtl number (
), Prandtl number ( ), Eckert number (
), Eckert number ( ) and unsteadiness parameter (
) and unsteadiness parameter (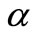 ). In order to verify the validity and accuracy of the present analysis, results for the local Nusselt number are compared with those reported by Chen [5], Swati et al. [15] and Ishak et al. [7] for steady flow over a linearly stretching sheet in the absence of magnetic field. The Comparison in the above cases is found to be in excellent agreement, as shown in Table 1. The problem mentioned here has many practical applications that includes both metal and polymer extrusion process. For instance, it occurs in the extrusion of a polymer sheet from a die or in the drawing of plastic films. It is also encountered in other process like annealing and tinning of copper wires, continuous casting, spinning of fibers, the aerodynamic extrusion of plastic sheets, crystal growing, drawing plastic films and glass blowing and so on.
). In order to verify the validity and accuracy of the present analysis, results for the local Nusselt number are compared with those reported by Chen [5], Swati et al. [15] and Ishak et al. [7] for steady flow over a linearly stretching sheet in the absence of magnetic field. The Comparison in the above cases is found to be in excellent agreement, as shown in Table 1. The problem mentioned here has many practical applications that includes both metal and polymer extrusion process. For instance, it occurs in the extrusion of a polymer sheet from a die or in the drawing of plastic films. It is also encountered in other process like annealing and tinning of copper wires, continuous casting, spinning of fibers, the aerodynamic extrusion of plastic sheets, crystal growing, drawing plastic films and glass blowing and so on.
Figure 1 illustrate the effect of magnetic parameter 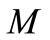 on velocity distributions for fluid and dust phase, when other parameters are fixed i.e.,
on velocity distributions for fluid and dust phase, when other parameters are fixed i.e.,  ,
,  ,
,  and
and . It can be seen that the momentum boundary layer thickness decreases as
. It can be seen that the momentum boundary layer thickness decreases as 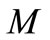 increases, and hence induces an increases in the absolute value of the velocity gradient at the surface. The effect of unsteadiness parameter
increases, and hence induces an increases in the absolute value of the velocity gradient at the surface. The effect of unsteadiness parameter 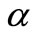 on velocity distribution for both fluid and dust phase as a function of
on velocity distribution for both fluid and dust phase as a function of 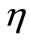 are shown in the Figure 2. It is very interesting to note that velocity profiles decreases with increase in the value of unsteadiness parameter, when
are shown in the Figure 2. It is very interesting to note that velocity profiles decreases with increase in the value of unsteadiness parameter, when ,
,  ,
,  ,
,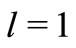 .
.

Table 1. Comparison of Local Nusselt number 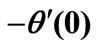 for several values of Pr with
for several values of Pr with .
.

Figure 1. Velocity profiles for the effect of Magnetic parameter M.
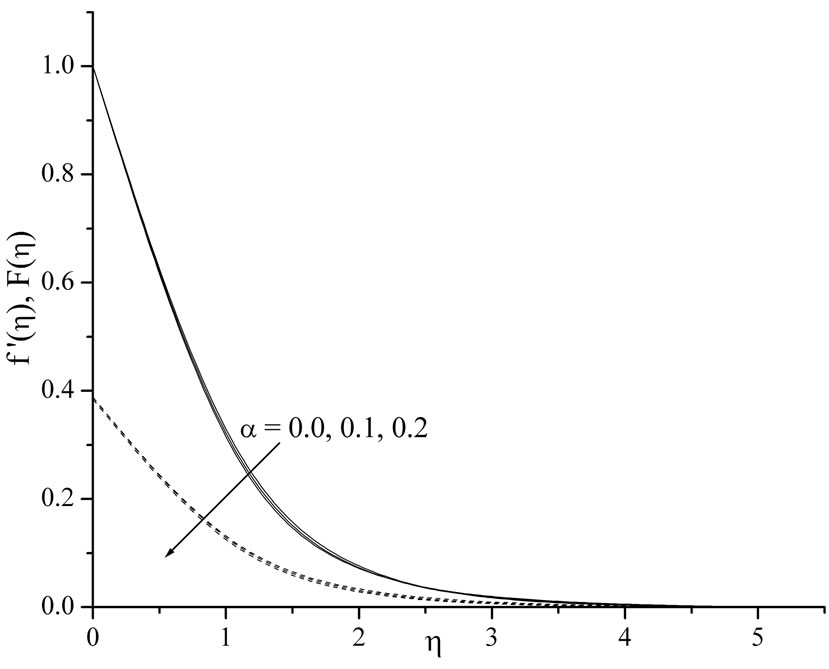
Figure 2. Velocity profiles for the effect of variable unsteadiness parame-ter α.
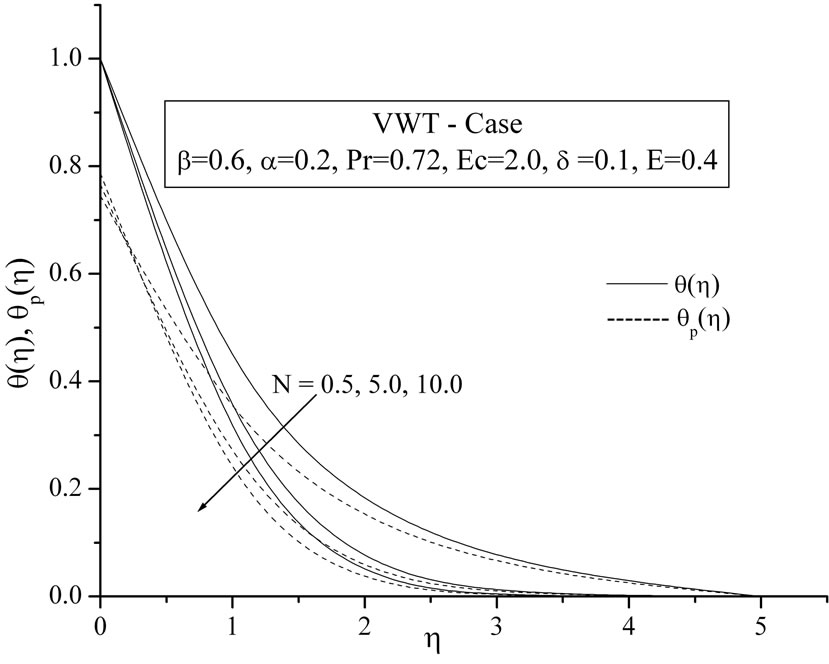
In Figures 3(a) and (b), the temperature components ,
, 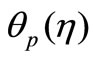 for VWT case and
for VWT case and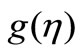 ,
,  for VHF case have been plotted for several values of the parameter
for VHF case have been plotted for several values of the parameter . From these figures, it is evident that the temperature components for both fluid and dust phase decreases with an increase in the fluid-particle interaction parameter
. From these figures, it is evident that the temperature components for both fluid and dust phase decreases with an increase in the fluid-particle interaction parameter .
.
Figures 4(a) and (b) displays the distribution of temperature for various values of unsteadiness parameter 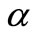 for VWT and VHF cases respectively. From these figures, it is seen that the temperature profiles decreases smoothly with
for VWT and VHF cases respectively. From these figures, it is seen that the temperature profiles decreases smoothly with  in the absence of unsteadiness parameter
in the absence of unsteadiness parameter 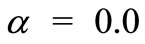 whereas the temperature profiles continuously decreases with increase in
whereas the temperature profiles continuously decreases with increase in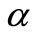 . This shows the important fact that the rate of cooling is much faster for higher values of unsteadiness parameter wher-eas it may take longer time for cooling during steady flows.
. This shows the important fact that the rate of cooling is much faster for higher values of unsteadiness parameter wher-eas it may take longer time for cooling during steady flows.
The effect of prandtl number  on heat transfer process may be analyzed from the Figures 5(a) and (b) in VWT and VHF cases respectively. These figures reveals that the temperature distribution continuously decrea-ses within the boundary layer for all values of
on heat transfer process may be analyzed from the Figures 5(a) and (b) in VWT and VHF cases respectively. These figures reveals that the temperature distribution continuously decrea-ses within the boundary layer for all values of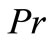 . This is consistence with the well known fact that the thermal boundary layer thickness decreases with increasing Prandtl number. Also, the temperature decreases at a faster rate for higher values of
. This is consistence with the well known fact that the thermal boundary layer thickness decreases with increasing Prandtl number. Also, the temperature decreases at a faster rate for higher values of . This shows that the rate of cooling is faster in the case of higher Prandtl number.
. This shows that the rate of cooling is faster in the case of higher Prandtl number.
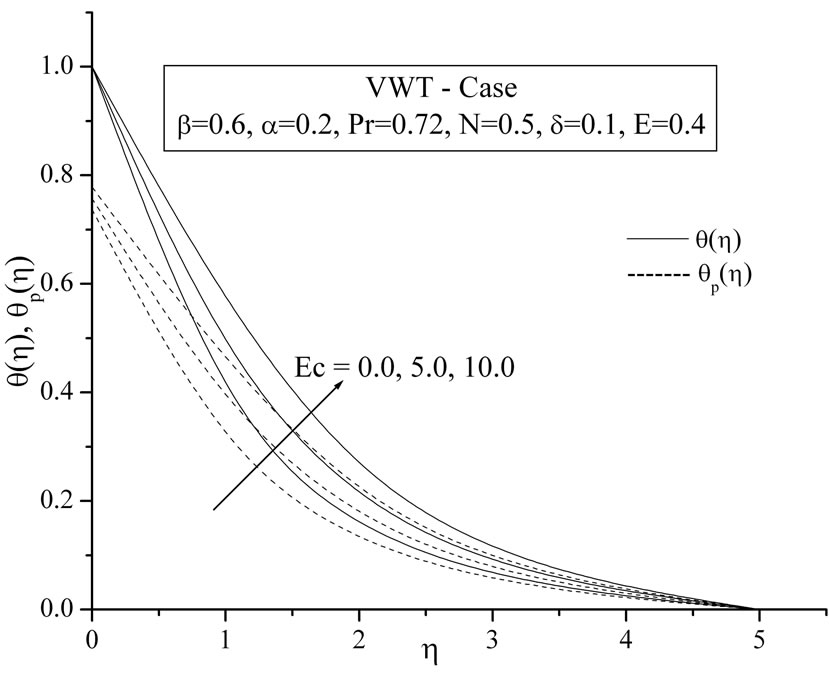
The plots Figures 6(a) and (b) show the temperature distribution versus distance  from the sheet, for different values of Eckert number
from the sheet, for different values of Eckert number 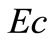 for both VWT and VHF cases respectively. By analyzing the graphs it reveals that the effect of increasing values of Eckert number is to increase the temperature distribution in flow region for both fluid and dust phase.
for both VWT and VHF cases respectively. By analyzing the graphs it reveals that the effect of increasing values of Eckert number is to increase the temperature distribution in flow region for both fluid and dust phase.
 (a)
(a)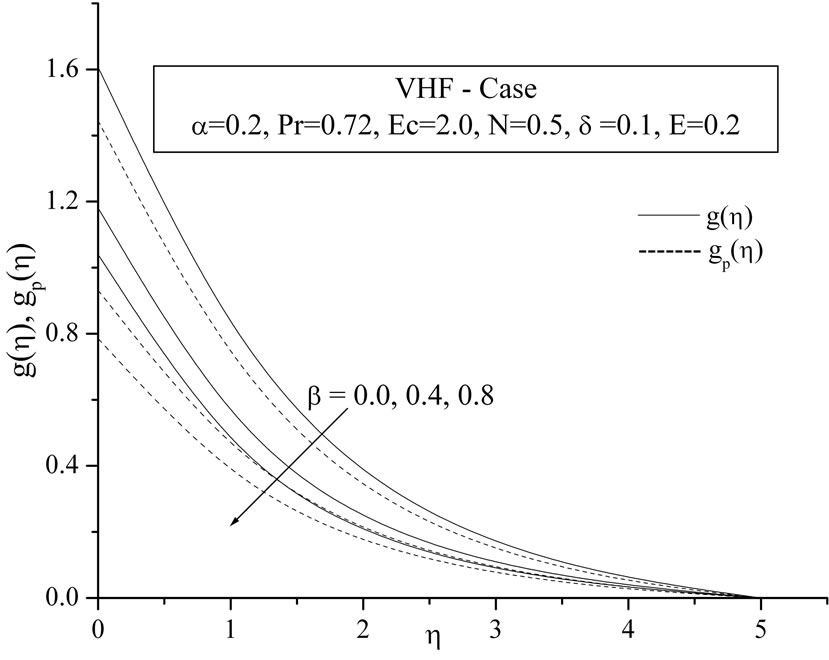 (b)
(b)
Figure 3. (a) Temperature profiles for variable fluid-interaction parameter β; (b) Tempera-ture profiles for variable fluidinteraction parameter β.
 (a)
(a) (b)
(b)
Figure 4. (a) Temperature profiles for variable fluid-interaction parameter β; (b) Tempera-ture profiles for variable fluidinteraction parameter β.
 (a)
(a)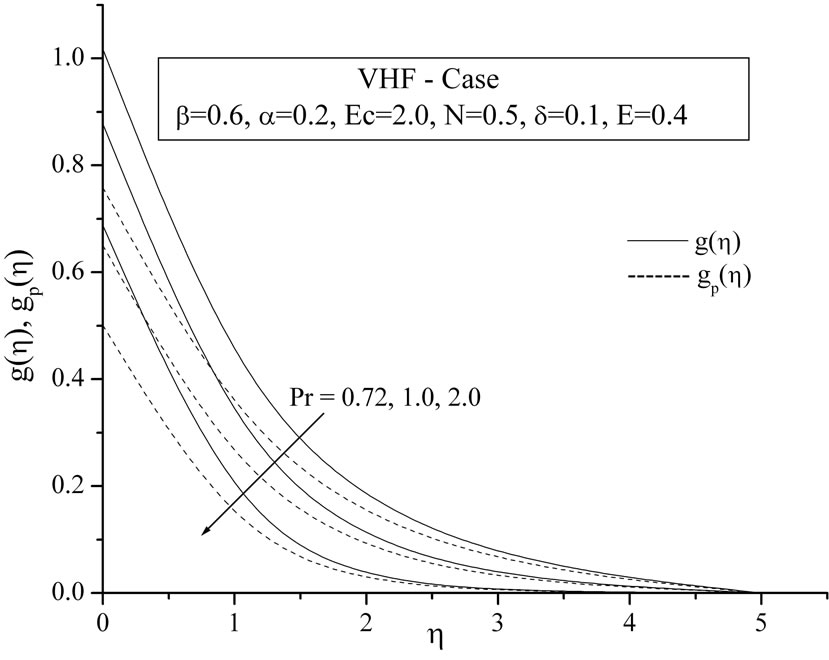 (b)
(b)
Figure 5. (a) Temperature profiles for the effect of Prandtl number Pr; (b) Temperature profiles for the effect of Prandtl number Pr.
 (a)
(a)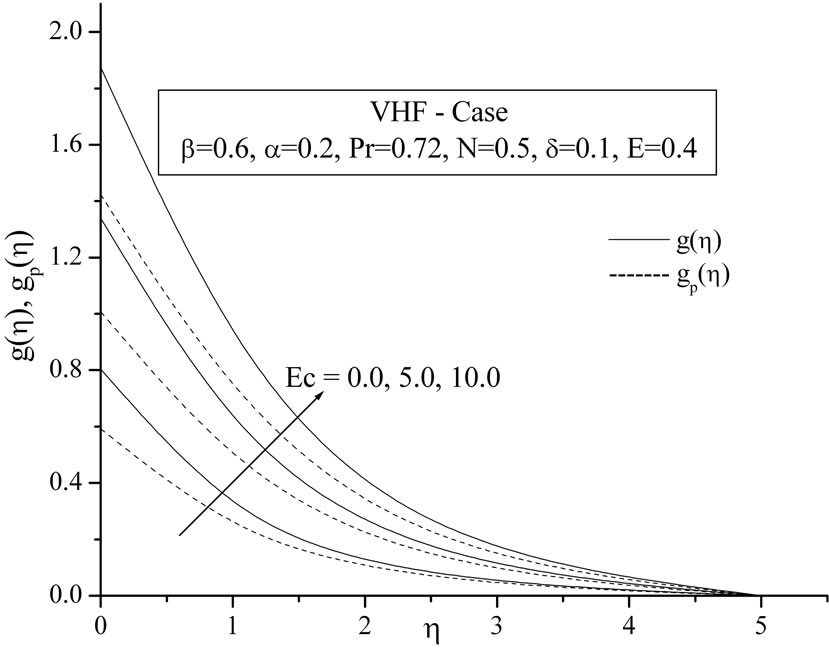 (b)
(b)
Figure 6. (a) Temperature profiles for the effect of Eckert number Ec; (b) Temperature profiles for the effect of Eckert number Ec.
Figures 7(a) and (b) depict the dimensionless temperature profiles versus  for different values of Number density
for different values of Number density , for both VWT and VHF cases respectively. Here we observed that the temperature profiles for both fluid and dust particles decreases with the increase of Number density.
, for both VWT and VHF cases respectively. Here we observed that the temperature profiles for both fluid and dust particles decreases with the increase of Number density.
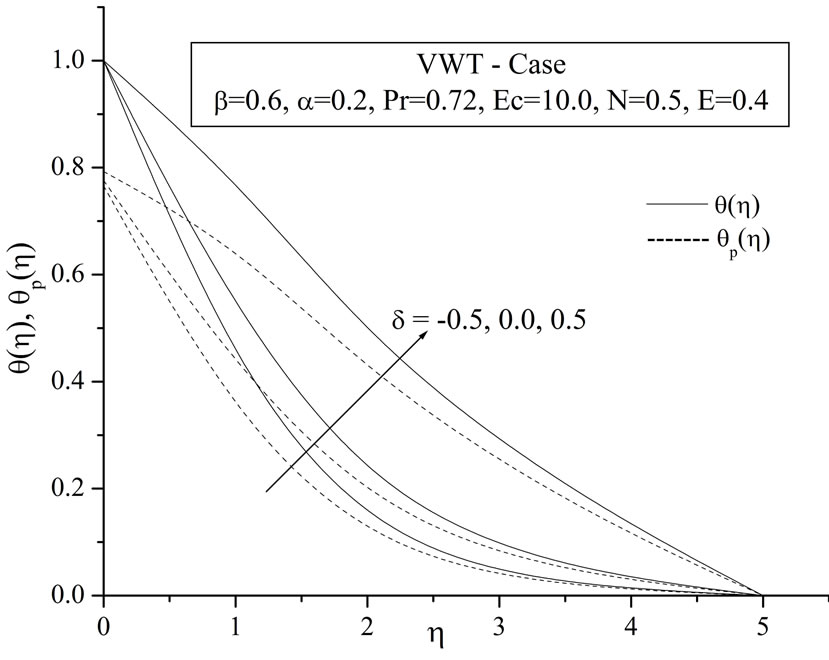
Figures 8(a) and (b) give variation of temperature distribution within the boundary layer for various values heat source/sink parameter  for VWT and VHF cases. It is noted that the temperature distribution decrease decreases with increase in the heat generation parameter whereas this trend is reverses during heat absorption.
for VWT and VHF cases. It is noted that the temperature distribution decrease decreases with increase in the heat generation parameter whereas this trend is reverses during heat absorption.
The impact of all the physical parameters on skin friction coefficient , wall temperature gradient
, wall temperature gradient  and temperature function
and temperature function  may be analyzed from the Table 2. It is interesting to note that the effect of magnetic parameter is to decrease the skin friction coefficient due to internal absorption parameter (
may be analyzed from the Table 2. It is interesting to note that the effect of magnetic parameter is to decrease the skin friction coefficient due to internal absorption parameter ( ). From this table, we also observed that the surface gradient
). From this table, we also observed that the surface gradient  decreases with increase in the unsteadiness parameter while the rate of heat transfer increases with unsteadiness parameter. Further, it is noticed that the effect of magnetic parameter is to decrease the surface gradient and also rate of heat transfer coefficients.
decreases with increase in the unsteadiness parameter while the rate of heat transfer increases with unsteadiness parameter. Further, it is noticed that the effect of magnetic parameter is to decrease the surface gradient and also rate of heat transfer coefficients.
6. Conclusions
Numerical solutions have been obtained to study the
 (a)
(a) (b)
(b)
Figure 7. (a) Temperature profiles for the effect of Number density N; (b) Temperature profiles for the effect of Number density N.
 (a)
(a)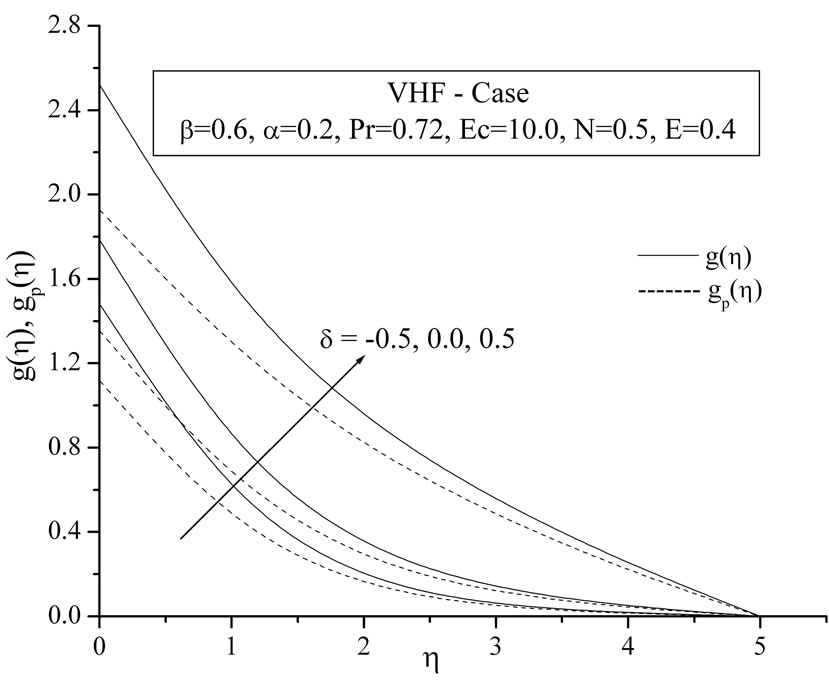 (b)
(b)
Figure 8. (a) Temperature profiles for the effect of heat source/sink parameter δ; (b) Temperature profiles for the effect of heat source/sink parameter δ.
boundary layer and heat transfer of a dusty fluid in a laminar flow of an incompressible viscous fluid past an unsteady stretching surface the presence of heat source/ sink. An appropriate similarity transformed was used to transform the system of time-dependent partial differential equations to a set of ordinary differential equations. The coupled ordinary differential Equations (9)-(12) and (18)-(19) for VWT case or (22)-(23) for VHF case are solved numerically by applying RKF-45 order method using Maple software. The temperature profiles  and
and 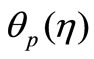 in VWT case and temperature profiles
in VWT case and temperature profiles 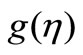 and
and  in VHF case are depicted graphically in the presence of internal heat generation/absorption (i.e.,
in VHF case are depicted graphically in the presence of internal heat generation/absorption (i.e., 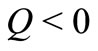 and
and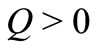 ). The effect of internal internal heat generation/absorption (non-uniform heat source/sink) is to dampen or enhance the heat transport in the linear fashion. The effects of various physical parameters such as
). The effect of internal internal heat generation/absorption (non-uniform heat source/sink) is to dampen or enhance the heat transport in the linear fashion. The effects of various physical parameters such as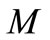 ,
,  ,
, 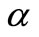 ,
,  ,
, 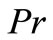 ,
,  and
and 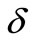 on the heat transfer characteristics were examined. Numerical computations show that the present values of local Nusselt number are in close agreement with those obtained by previous investigators in the absence of
on the heat transfer characteristics were examined. Numerical computations show that the present values of local Nusselt number are in close agreement with those obtained by previous investigators in the absence of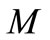 ,
, 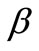 ,
,  ,
, 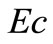 and
and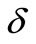 . The values of thermal heat characteristics at the wall temperature gradient function
. The values of thermal heat characteristics at the wall temperature gradient function 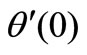 (for VWT Case) and wall temperature
(for VWT Case) and wall temperature 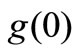 (for VHF Case) are tabulated in Table 3.
(for VHF Case) are tabulated in Table 3.
In the light of the present investigation, the following conclusions are drawn:
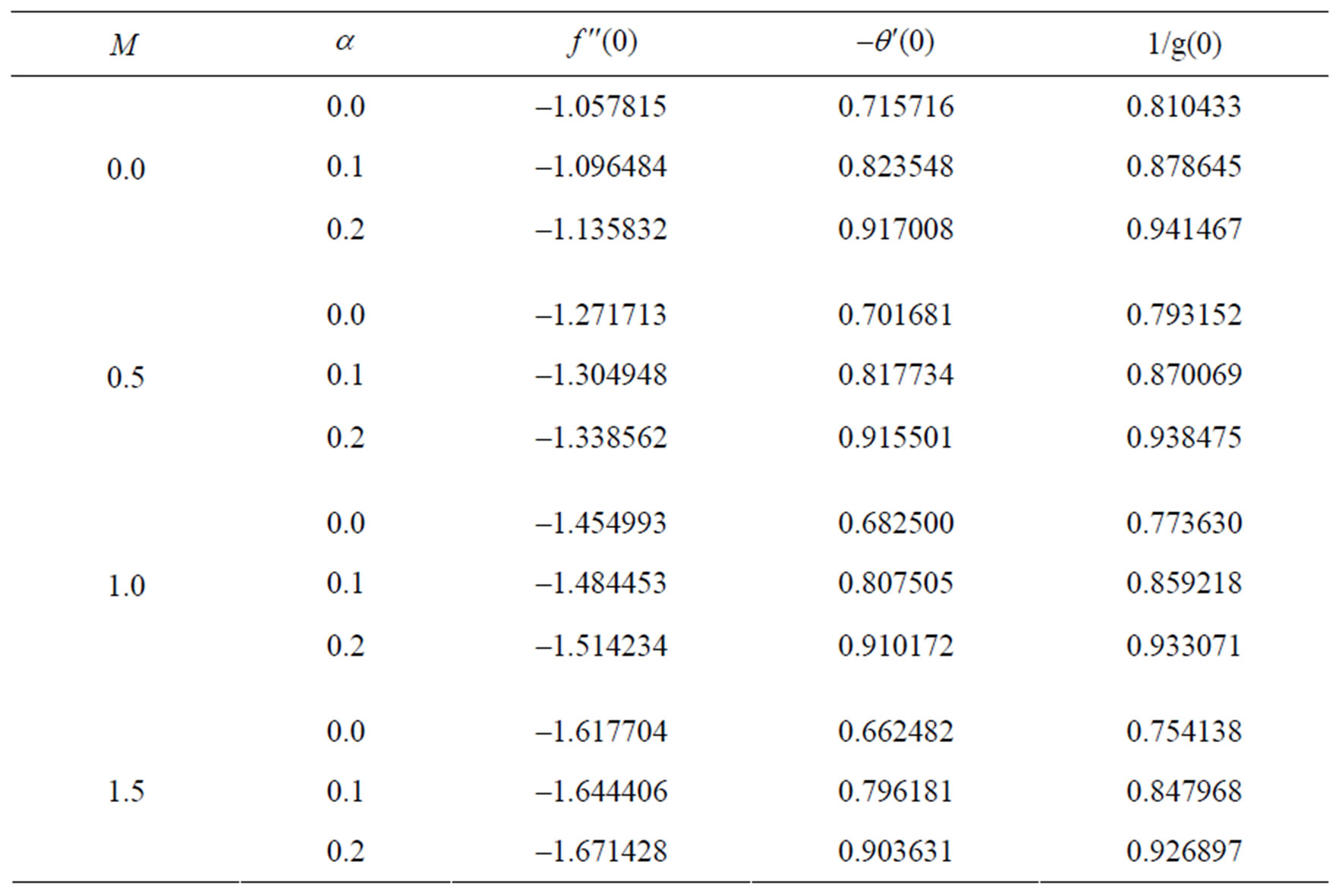
Table 2. Results of skin friction coefficient and local Nusselt number for various values of M and α when Pr = 0.72, Ec = 2.0, δ = 0.1, β = 0.4.

Table 3. Values of wall temperature gradient 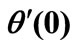 (for VWT Case) and wall temperature
(for VWT Case) and wall temperature 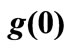 (for VHF Case).
(for VHF Case).
• The thickness of the momentum boundary layer decreases with increasing the magnetic parameter and unsteadiness parameter.
• In both VWT and VHF cases, the temperature decreases with an increase in the value of unsteadiness parameter which is consistent with the fact that the thermal boundary layer thickness decreases with increase in the unsteadiness parameter in the presence of heat source/sink parameter.
• The temperature profiles decreases with increasing the values of Prandtl number, number density and fluidparticle interaction parameter.
• The surface gradient is negative and decreases with increasing unsteadiness parameter and magnetic parameter.
• The temperature increases with an increase in the value of Eckert number and heat source/sink parameter. The flow of heat becomes faster when Eckert number increases.
• The value of local Nusselt number increases with increasing unsteadiness parameter for both VWT and VHF cases respectively, whereas reverse trend is seen with increasing magnetic number.
7. Acknowledgements
We wish to express our thanks to DST (Department of Science and Technology), New Delhi for financial support to pursue this work under a Major Research Project (Grant no: SR/S4/MS: 470/07, 25-08-2008).
8. REFERENCES
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: I. Boundary Layer Equations for Two Dimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- L. J. Grubka and K. M. Bobba, “Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature,” International Journal of Heat and Mass Transfer, Vol. 107, No. 1, 1985, pp. 248-250.
- L. J. Crane, “Flow Past a Stretching Plate,” Zeitschrift fr Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647.
- K. Vajravelu and J. Nayfeh, “Hydromagnetic Flow of a Dusty Fluid over a Stretching Sheet,” International Journal of Non-linear Mechanics, Vol. 27, No. 6, 1992, pp. 937-945. doi:10.1016/0020-7462(92)90046-A
- C. H. Chen, “Laminar Mixed Convection Adjacent to Vertical Continuously Stretching Sheets,” Heat Mass Transfer, Vol. 33, No. 5-6, 1998, pp. 471-476. doi:10.1007/s002310050217
- M. S. Abel, P. G. Siddeshwar and M. M. Nandeppanavar, “Heat Transfer in a Viscoelastic Boundary Layer Flow over a Stretching Sheet with Viscous Dissipation and Non-uniform Heat Source,” International Journal of Heat and Mass Transfer, Vol. 50, No. 5-6, 2007, pp. 960-966. doi:10.1016/j.ijheatmasstransfer.2006.08.010
- A. Ishak, R. Nazar and I. Pop, “Hydromagnetic Flow and Heat Transfer Adjacent to a Stretching Vertical Sheet,” Heat Mass Transfer, Vol. 44, No. 8, 2008, pp. 921-927. doi:10.1007/s00231-007-0322-z
- A. Aziz, “A Similarity Solution for Laminar Thermal Boundary Layer over a Flat Plate with a Convective Surface Boundary Condition,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 4, 2009, pp. 1064-1068. doi:10.1016/j.cnsns.2008.05.003
- E. M. A. Elbashbeshy and M. A. A. Bazid, “Heat Transfer in a Porous Medium over a Stretching Sheet with Internal Generation and Suction or Injection,” Applied Mathematics and Computation, Vol. 158, No. 3, 2004, pp. 799- 807. doi:10.1016/j.amc.2003.08.141
- H. I. Andersson, J. B. Aareseth and B. S. Dandapat, “Heat Transfer in a Liquid Film on an Unsteady Stretching Surface,” International Journal of Heat and Mass Transfer, Vol. 43, No. 1, 2000, pp. 69-74. doi:10.1016/S0017-9310(99)00123-4
- E. M. A. Elbashbeshy and M. A. A. Bazid, “Heat Transfer over an Unsteady Stretching Surface,” Heat and Mass Transfer, Vol. 41, No. 1, 2004, pp. 1-4. doi:10.1007/s00231-004-0520-x
- S. Sharidan, T. Mahmood and I. Pop, “Similarity Solutions for the Unsteady Boundary Layer Flow and Heat Transfer Due to a Stretching Sheet,” International Journal of Applied Mechanics and Engineering, Vol. 11, No. 3, 2008, pp. 647-654.
- R. Tsai, K. H. Huang and J. S. Huang, “Flow and Heat Transfer over an Unsteady Stretching Surface with a Non-uniform Heat Source,” International Communications in Heat and Mass Transfer, Vol. 35, No. 10, 2008, pp. 1340-1343. doi:10.1016/j.icheatmasstransfer.2008.07.001
- A. Ishak, R. Nazar and I. Pop, “Heat Transfer over an Unsteady Stretching Permeable Surfaec with Prescribed Wall Temperature,” Non-linear Analysis: Real World Applications, Vol. 10, No. 5, 2009, pp. 2909-2913. doi:10.1016/j.nonrwa.2008.09.010
- S. Mukhopadhyay and H. I. Andersson, “Effect of Slip and Heat Transfer Analysis of Flow over an Unsteady Stretching Surface,” Heat Mass Transfer, Vol. 45, No. 11, 2009, pp. 1447-1452. doi:10.1007/s00231-009-0516-7
- D. Pal and P. S. Hiremath, “Computational Modelling of Heat Transfer over an Unsteady Stretching Surface Embedded in a Porous Medium,” Meccanica, Vol. 45, No. 3, 2010, pp. 415-424. doi:10.1007/s11012-009-9254-7
- H. Schlichting, “Boundary Layer Theory,” McGraw-Hill, New York, 1968.

