Engineering
Vol. 3 No. 2 (2011) , Article ID: 4288 , 4 pages DOI:10.4236/eng.2011.32019
The Research of the Flow of Bodies with Use of the Vector Form of the Newton’s Law for the Viscous Liquid
Department of Physics, Samara State University, Samara, Russia
E-mail: volobuev@samaramail.ru
Received January 11, 2011; revised January 16, 2011; accepted January 18, 2011
Keywords: Newton’s Law for Viscosity, A Body Flow, Circulation of Speed, Resistance Factor, A Viscosity Tensor
ABSTRACT
On the basis of the vector formula of the Newton’s law for a viscous liquid and the integra-ted vector form of the equation of an impulse for a viscous liquid for resistance and carrying power of a profile of any form and the big length dependences are found in a stream. Application of the found dependences at a circulating flow of the cylinder located across a stream is showed. The analysis of a tensor of viscosity for laminar and turbulent flow is carried out.
1. Introduction
The cross-section flow around of bodies of any profile arises at flights of planes, movement of hydrofoils, on wires of lines of a high voltage etc. The big contribution to the decision of a problem of a flow wingeous profile a stream of an ideal liquid was brought by outstanding scientist N. E. Zhukovsky’s formula for carrying power calculation, has a strict substantiation and is widely used in aerodynamic calculations [1,2].
2. The Equation of a Impulse
At the decision of problems of a flow of bodies, for example, wingeous profile the integrated form of the impulse equation is interesting. Let’s find this form, using the equation of 2nd Newton’s law for elementary volume of a liquid dW in a following kind:
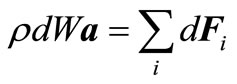 , (1)
, (1)
where a—acceleration of the allocated volume dW, r— liquid density,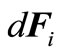 —the forces operating on the allocated volume of a liquid.
—the forces operating on the allocated volume of a liquid.
Writing acceleration in the form of the sum of local and convective components, we will receive:
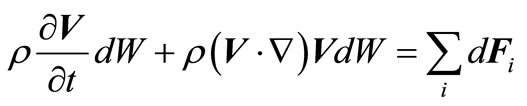 . (2)
. (2)
Let’s integrate on volume the left and right members of Equation (2):
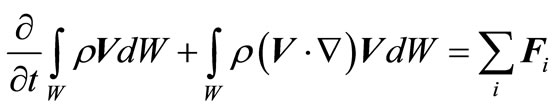 . (3)
. (3)
Let’s designate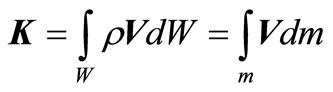 —A local component of quantity of movement of a liquid in weight dm in volume dW. Besides, we will use the theorem of the vector analysis [3]
—A local component of quantity of movement of a liquid in weight dm in volume dW. Besides, we will use the theorem of the vector analysis [3]
 . Believing a liquid incompressible, i.e.
. Believing a liquid incompressible, i.e.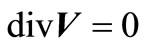 , we have:
, we have:
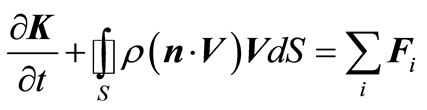 , (4)
, (4)
where S—The area of a surface limiting volume W.
The formula (4) represents the integrated form of the equation of an impulse [4].
3. A Flow Around of Bodies by the Viscous Liquid
Let’s find the amendment to the formula Zhukovsky for the carrying power, arising at the expense of viscosity of a stream of a liquid.
This correcting is carried out by addition to the formula of carrying power of some, poorly proved, additional composed till now [5]. In this case it is noticed that viscosity influence is double: first, it leads to carrying power change, and secondly, there is a force of resistance to a flow.
Let’s consider some body Т which is permanently flowed round by a viscous liquid with accumulating speed  and we will find the main (total) vector of forces with which the liquid operates on a body at its continuous flow, Figure 1. Axis Y we will direct perpendicularly to drawing. In a direction of axis Y we will originally consider the size of a body unlimited, and the area of cross-section section invariable.
and we will find the main (total) vector of forces with which the liquid operates on a body at its continuous flow, Figure 1. Axis Y we will direct perpendicularly to drawing. In a direction of axis Y we will originally consider the size of a body unlimited, and the area of cross-section section invariable.
Let some any contour abcd covers this body.
On a liquid between a body and a contour abcd three forces operate: pressure force –Fp from external in relation to a contour abcd liquids, force of a friction from external, in relation to this contour, a liquid 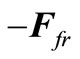 and force from body Т which we will designate –R. We consider that positive values of forces operate on the contrary, from a liquid between a body and a contour abcd, so that, for example, R—The force operating on body Т from a liquid. The finding of last force also is the main task of the given research.
and force from body Т which we will designate –R. We consider that positive values of forces operate on the contrary, from a liquid between a body and a contour abcd, so that, for example, R—The force operating on body Т from a liquid. The finding of last force also is the main task of the given research.
Believing a profile flow stationary, the integrated Equation (4), with the account  and
and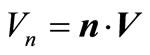 , it is possible to write down in a kind:
, it is possible to write down in a kind:
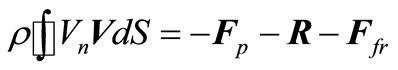 . (5)
. (5)
Pressure force is equal:
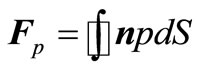 , (6)
, (6)
where р—Pressure in a liquid.
Using for force of a friction the vector form of the Newton’s law for viscosity in the form [6], we will find:
 . (7)
. (7)
Hence, it is possible to present the Equation (5) in a kind:
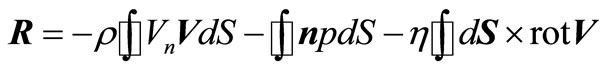 . (8)
. (8)
The vertical component of force R, concerning speed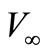 , Figure 1, a stream running on body Т, is carrying power, a horizontal component—Force of resistance to a flow. For a finding of these forces it is necessary to know pressure communication р and speeds of a liquid V.
, Figure 1, a stream running on body Т, is carrying power, a horizontal component—Force of resistance to a flow. For a finding of these forces it is necessary to know pressure communication р and speeds of a liquid V.
The Equation (8) allows to solve essentially a problem of a flow a viscous liquid of a profile of any form. Most interesting from the practical point of view the established flow of a body a liquid concerning small viscosity (air), therefore, with some approach, we will accept communication of pressure and speed of a flow according to the equation of Bernulli:
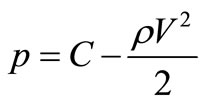 , (9)
, (9)
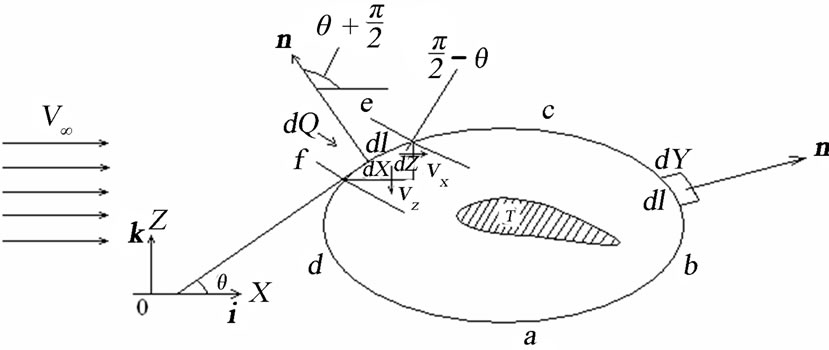
Figure 1. The flow of bodies of any profile at the stream of a viscous liquid.
where C—is a constant.
Substituting (9) in (8), we will receive:
 .(10)
.(10)
Let’s consider crossing by a running liquid of the allocated contour, Figure 1.
The external normal n is connected with ортами coordinates i, j, k and a corner q between axis Х and a tangent to a contour. Between a normal n and axis Х a corner
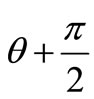 .
.
Hence:
 .(11)
.(11)
In last composed (10) we use a parity 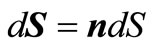 and the formula:
and the formula:
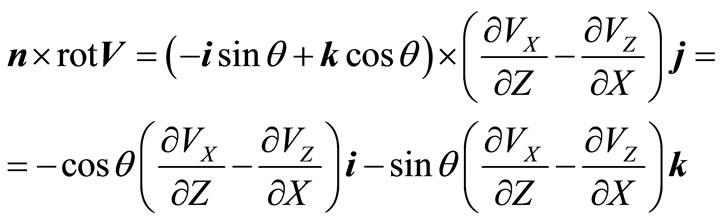 , (12)
, (12)
where VX and VZ—Components of a vector of speed V.
Substituting (11) and (12) in the formula (10), we have:
 (13)
(13)
At substitution we used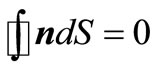 .
.
Projecting (13) on an axis of coordinates, we find making forces R:
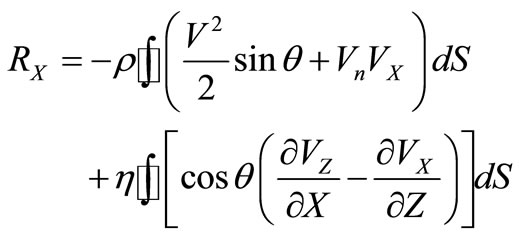 . (14)
. (14)
 . (15)
. (15)
In the further transformations we used 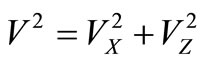 also parities, Figure 1 see:
also parities, Figure 1 see:
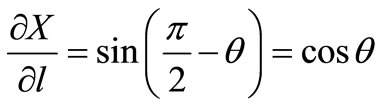 or
or 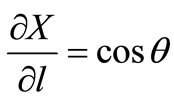
and
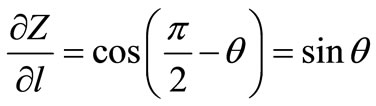 .(16)
.(16)
Besides, we use also:
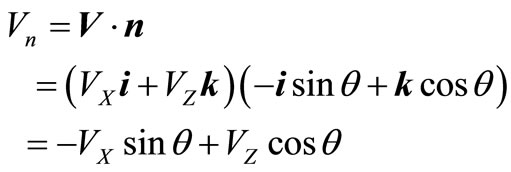 .
.
After corresponding substitutions, formulas (14) and (15) will be transformed to a kind:
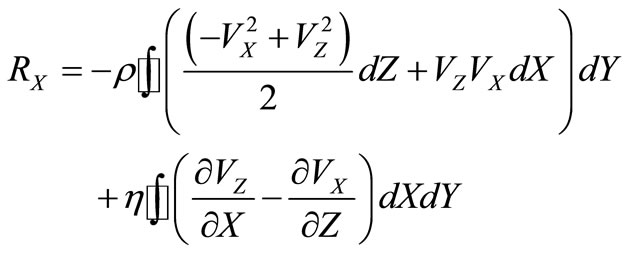 . (17)
. (17)
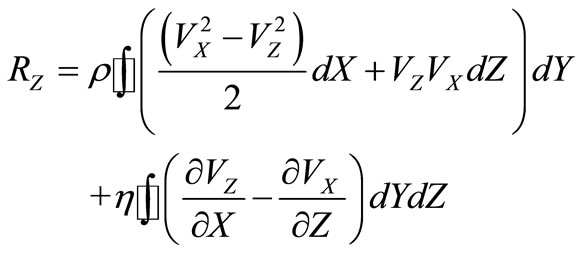 . (18)
. (18)
In difference, for example, from [1,2] the analysis of a flow of a body we will spend, using flow function y, without entering potential of speed. It is connected by that the potential flow is considered not.
Projections of speed to coordinate axes are connected with flow function:
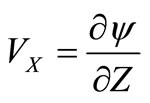 and
and . (19)
. (19)
Let’s accept:
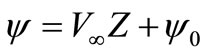 ,
,  ,
,  , (20)
, (20)
where the first composed y characterizes a homogeneous stream of a liquid [4], and the second non-uniform conditions of a flow of a body.
Substituting (20) in (17) and (18), we are limited only composed, not containing squares and products derivative from . It is connected by that far from a body derivative from
. It is connected by that far from a body derivative from  quickly aspire to zero—A flow homogeneous. Actually, we are limited to linear approach of a flow of a body by a liquid. It is as a result found:
quickly aspire to zero—A flow homogeneous. Actually, we are limited to linear approach of a flow of a body by a liquid. It is as a result found:
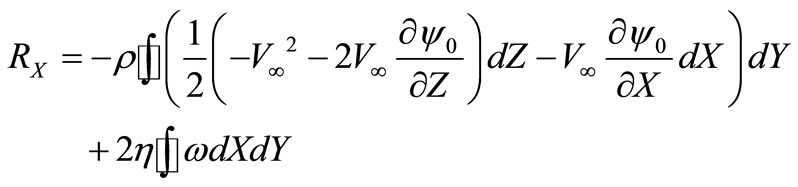 (21)
(21)
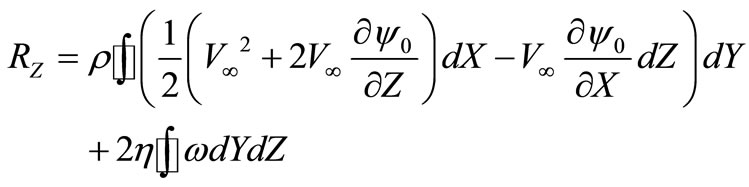 (22)
(22)
where it is designated —Angular speed of rotation of a liquid round a stream-line body [7]. The sign before last composed is defined by positivity of last composed in (21) since making
—Angular speed of rotation of a liquid round a stream-line body [7]. The sign before last composed is defined by positivity of last composed in (21) since making —is the force operating on a body from a liquid at the expense of its viscosity, equal on the module to force of resistance of a streamline body.
—is the force operating on a body from a liquid at the expense of its viscosity, equal on the module to force of resistance of a streamline body.
Using taking into account (16) conditions
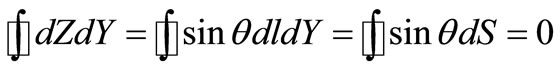 and
and
 , we will find:
, we will find:
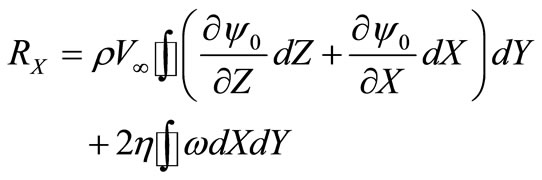 . (23)
. (23)
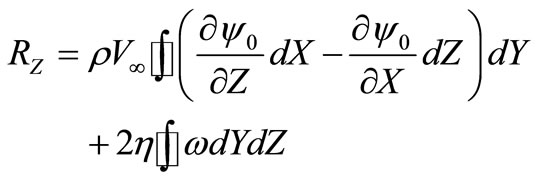 . (24)
. (24)
On Figure 1 the elementary expense of a liquid dQ through a contour abcd between two lines of a flow e and f is shown. The full expense Q of a liquid having on unit of length Y forming cylinder, entered or left a contour abcd is equal to zero. At the proof of the given position we use Green’s formula. According to [4], we have:
 . (25)
. (25)
The factor in the first integral in (24) represents circulation of speed [4] on unit of length Y forming the cylinder:
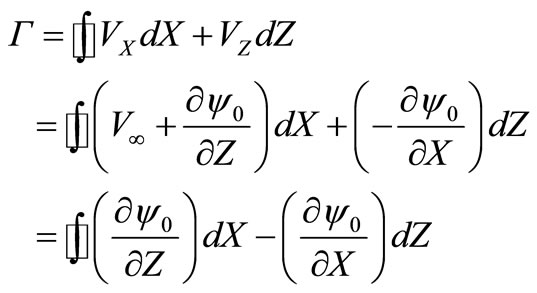 . (26)
. (26)
Using linear dependence of projections of force R on coordinate Y, taking into account (25) and (26) we will write down (23) and (24) in a kind:
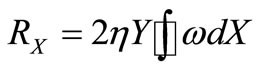 , (27)
, (27)
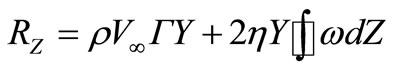 . (28)
. (28)
Under size Y in this case we mean the size of a streamline body in a direction of axis Y. At 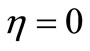 from (28) we have the Zhukovsky’s formula for carrying power.
from (28) we have the Zhukovsky’s formula for carrying power.
Formulas (27) and (28) allow to calculate basically force of resistance 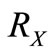 and
and 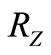 carrying power in a viscous stream for bodies of any form.
carrying power in a viscous stream for bodies of any form.
Originally we will show that for an ideal liquid additional viscous composed in (27) and (28) are equal to zero owing to not only formal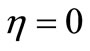 , but also at the expense of arising structure of a stream. For example, for a case uncirculatation flows of the circular cylinder, i.e. at
, but also at the expense of arising structure of a stream. For example, for a case uncirculatation flows of the circular cylinder, i.e. at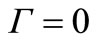 , with use of function
, with use of function 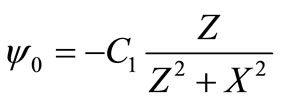 [4] where
[4] where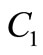 —A constant, direct calculation it is possible to show,
—A constant, direct calculation it is possible to show, 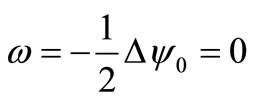 as both making forces R are equal in approach of an ideal liquid to zero.
as both making forces R are equal in approach of an ideal liquid to zero.
Let’s consider a circulating flow of the cylinder in radius b an ideal liquid. We will accept communication between speed of a stream and circulation in the form of  [4], where r—distance from a cylinder axis.
[4], where r—distance from a cylinder axis.
Angular speed we will find from a condition 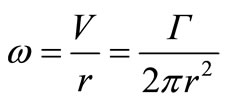 , where
, where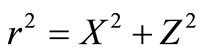 . Circulation we will consider as a constant [5]. Speed of a circulating component of a stream thus falls in inverse proportion to distance from the cylinder center. Substituting expression for angular speed in formulas (27) and (28), we will find:
. Circulation we will consider as a constant [5]. Speed of a circulating component of a stream thus falls in inverse proportion to distance from the cylinder center. Substituting expression for angular speed in formulas (27) and (28), we will find:
 , (29)
, (29)
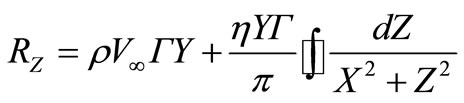 . (30)
. (30)
Integrals in (29) and (30) are equal among themselves from a condition of coordinate symmetry. These integrals are simple for calculating, using Green’s formula. For example, integral
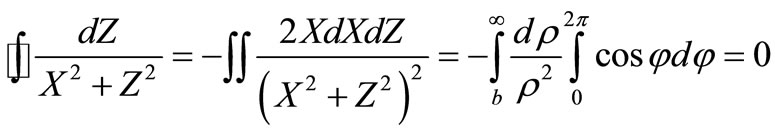 where transition to polar coordinates is carried out. Hence, both viscous additives to components of force R are equal to zero.
where transition to polar coordinates is carried out. Hence, both viscous additives to components of force R are equal to zero.
The finding of expressions convenient for calculation viscous composed for components of force R at a flow a liquid of any profiles is generally exclusively challenge.
For example, for the cylinder the formula (27), using Figure 2, it is possible to transform as follows:
 . (31)
. (31)
Integration limits in (31) are defined by the following. We consider only area of monotonously growing dependence of projection VX from a corner j where flow lines have circular character. With corner increase j from some minimum value which it is approximately considered equal to zero, to value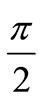 , the longitudinal component of speed
, the longitudinal component of speed 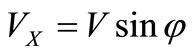 grows from some minimum to the maximum value, which on some small distance from the cylinder equally
grows from some minimum to the maximum value, which on some small distance from the cylinder equally . Then VX again falls almost to zero. A thickness of an interface it is considered by the small. In vicinities of points A and B, Figure 2, stream structure it is complicated. The strong bend of lines of a flow is observed. Therefore the received result (31) which are not considering features of these areas, the confidant. Attracts attention absence of dependence of force
. Then VX again falls almost to zero. A thickness of an interface it is considered by the small. In vicinities of points A and B, Figure 2, stream structure it is complicated. The strong bend of lines of a flow is observed. Therefore the received result (31) which are not considering features of these areas, the confidant. Attracts attention absence of dependence of force  from cylinder radius b. This effect, proceeding from the dimension analysis, is marked in [8]. It vanishes at transition to nonlinear approach in calculations.
from cylinder radius b. This effect, proceeding from the dimension analysis, is marked in [8]. It vanishes at transition to nonlinear approach in calculations.
The question on dependence of force of resistance to a flow a viscous liquid of the cylinder from its radius is of interest. From the analysis of the spent calculation follows that existence of circular lines of a flow, Figure 2doesn’t lead to dependence of force RX on radius. But in vicinities of points A and B sharp change of a direction of these lines is observed, there are points of an excess of lines of a flow. It is known that at sharp reduction of radius of the pipeline where the excess of lines of a flow
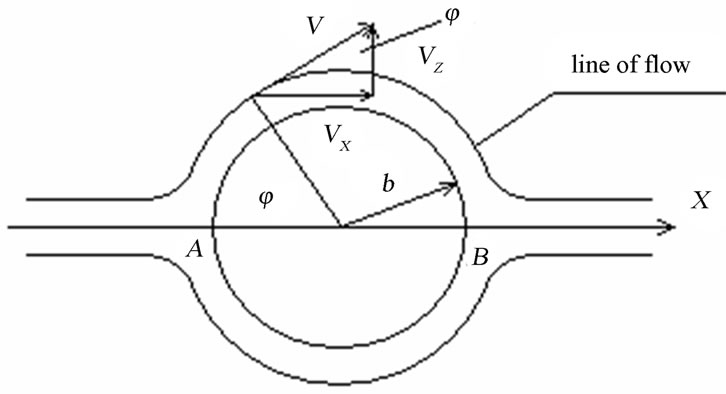
Figure 2. The form of the lines of a flow and speeds components VX, VZ at the cross-section flow of the cylinder a viscous liquid.
also is observed, there is a loss of static pressure in a flow viscous liquid which is spent for maintenance of a constancy of dynamic pressure [9]. The same process should be observed in vicinities of points A and B. Sharp changes of kinetic energy of a stream at an excess of lines of a flow, basically, are described convective nonlinear composed in the equation of an impulse (2). Therefore, only at the account of this composed there can be a dependence of force RX on radius, as proves to be true in [8].
Dependence of factor of resistance of the cylinder on Reynolds’s number in approach (31) looks like:
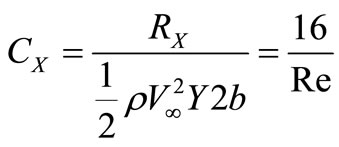 , (32)
, (32)
where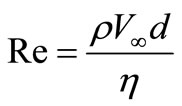 , diameter of the cylinder
, diameter of the cylinder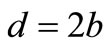 .
.
On Figure 3 the attitude of factor of the resistance  [10] found taking into account nonlinear convective composed
[10] found taking into account nonlinear convective composed 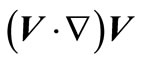 at decision the equation of an impulse in the differential form, to the factor of resistance found under the formula (32) is shown. The formula (32) states a quite good estimation of factor of resistance of the cylinder in area
at decision the equation of an impulse in the differential form, to the factor of resistance found under the formula (32) is shown. The formula (32) states a quite good estimation of factor of resistance of the cylinder in area  .
.
Let’s estimate carrying power increase at a circulating flow of the cylinder, arising at the expense of viscosity. We will transform the formula (28) similarly transformation (31):
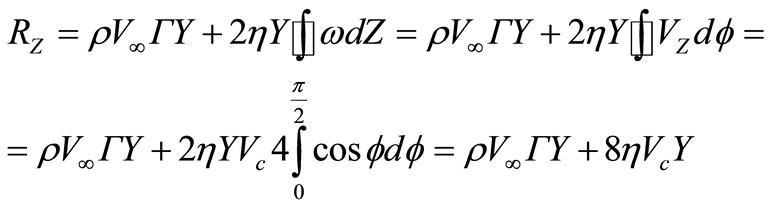 .(33)
.(33)
Not circulating component 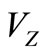 at integration on the closed contour can to be considered, since it is symmetric concerning axis Х, with change of a direction in the course of integration.
at integration on the closed contour can to be considered, since it is symmetric concerning axis Х, with change of a direction in the course of integration.
Circulating component of district speed Vc, arising, for example, at cylinder rotation, we will connect since corresponding this speed circulation Г1 under the formula  , as a result we will find:
, as a result we will find:
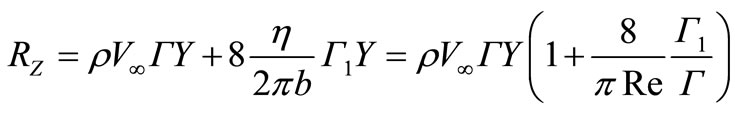 . (34)
. (34)
Let’s notice that at increase in number of Reynolds carrying power to aspire to that at a circulating flow of the cylinder an ideal liquid. If the circulating component
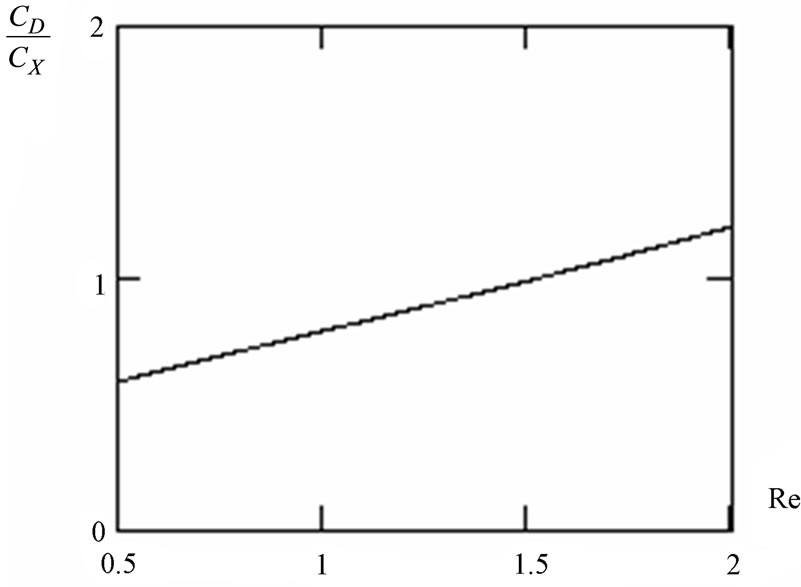
Figure 3. Dependence of the ratio of factors of resistance of the cylinder in the stream at the account СD and not the account СX of nonlinear effects in a flow of a liquid depending on Reynolds’s number.
of speed is defined only by cylinder rotation, for example, at the problem decision on occurrence of effect of Magnus [10] at falling of the cylinder rolling down from a table on a floor the first composed in the formula (34) to consider there is no necessity. The first composed in (34) needs to be considered only at circulation occurrence not connected with effects of viscosity, for example, around wingeous a profile at the expense of a certain angle of attack.
4. Tensor of Viscosity
We will analyse Newton’s law for force of viscosity (7) in more details. More the general view of this law looks like:
 , (35)
, (35)
where dS—A vector of the area of contact of layers of a liquid.
Generally viscosity![]() —Tensorous size (affinor) the second rank (i = 1, 2, 3 and j = 1, 2, 3) since it is the linear operator at transition from one vector to another. In coordinate representation the formula (35) can be copied in a kind
—Tensorous size (affinor) the second rank (i = 1, 2, 3 and j = 1, 2, 3) since it is the linear operator at transition from one vector to another. In coordinate representation the formula (35) can be copied in a kind . At calculation, for example, flow of liquid crystals it is necessary to consider tensorous character of viscosity [11].
. At calculation, for example, flow of liquid crystals it is necessary to consider tensorous character of viscosity [11].
Believing vector bases at the left and on the right in equality (35) identical, we find that
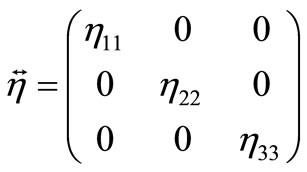 , i.e. a matrix of a tensor
, i.e. a matrix of a tensor ![]() the diagonal. Hence, there are three various factors of viscosity on three coordinate axes.
the diagonal. Hence, there are three various factors of viscosity on three coordinate axes.
If to consider a liquid newtonous, i.e. all components of a tensor of viscosity the identical . Therefore the formula (35) becomes simpler to (7).
. Therefore the formula (35) becomes simpler to (7).
The viscosity tensor becomes not diagonal at transition to liquid turbulent flow. In this case it looks like:
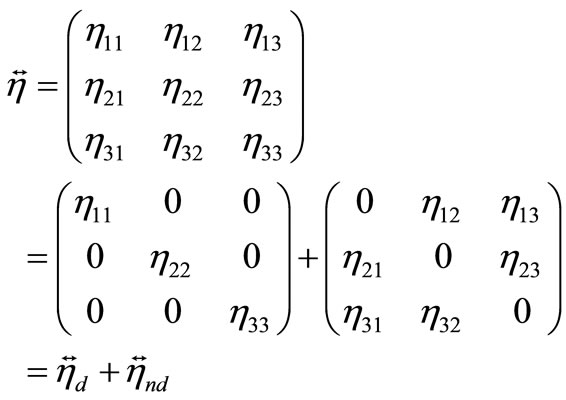 . (36)
. (36)
And the tensor  represents molecular viscosity, and
represents molecular viscosity, and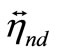 —Turbulent viscosity. We will notice that the tensor (36) is symmetric
—Turbulent viscosity. We will notice that the tensor (36) is symmetric .
.
Using the equation of an impulse (4), and also applying Reynolds’s method of decomposition of speed upon average and pulsation components , we find Reynolds’s pressure:
, we find Reynolds’s pressure:
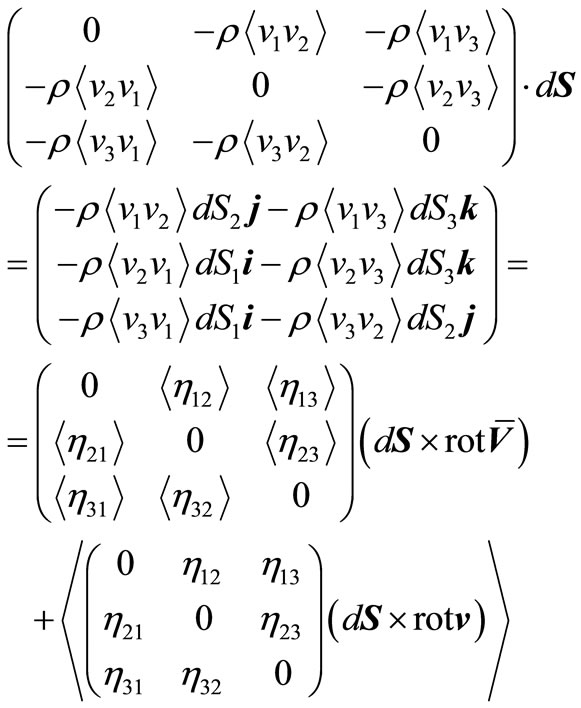 , (37)
, (37)
where i, j, k—is unit vectors and angular brackets is mean sign [12].
For example in flat geometry, for one of a component of a tensor of pressure of Reynolds it is simple to receive the formula:
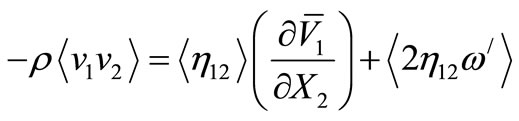 , (38)
, (38)
where 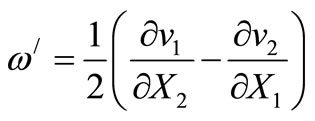 and
and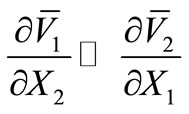 .
.
Let’s notice that unlike a hypothesis of Bussineska [7] for turbulent pressure, they remain 3 and at , i.e. in case of homogeneous and isotropic turbulence [13], for example, in a stream of gas after a frequent lattice.
, i.e. in case of homogeneous and isotropic turbulence [13], for example, in a stream of gas after a frequent lattice.
5. Conclusions
Use of the vector form of the Newton’s law for a viscous liquid allows to solve a problem of a flow around of bodies. Application of the found dependences at a circulating flow of the cylinder located across a stream is showed. In article the way of taking into consideration viscosity at correction N. E. Zhukovsky’s elevating force is showed. Factor of viscosity carries tensor character. The tensor of viscosity includes as molecular, so turbulent viscosity.
6. REFERENCES
- N. Е. Zhukovsky, “About the Contours, Supporting Surfaces of Airplanes,” The state publishing house techniq-teoret, Moscow, 1949.
- N. E. Zhukovsky, “Geometrical of Research about a Flow of Couette,” The state publishing house techniq-teoret, Moscow, 1949.
- V. G. Levich, “Course of the Theoretical Physics,” Physmathlit, Moscow, 1962.
- L. G. Lojtsansky, “Mechanics of a Liquid and Gas,” 7th Edition, Drofa, Moscow, 2003.
- G. N. Abramovich, “Applied Gas Dynamics,” Science, Moscow, 1969.
- A. N. Volobuev, V. I. Koshev and E. S. Petrov, “Boiphysical Principles of Hemodynamics,” Nova Science Publishers, Inc., New York, 2010.
- G. Schlichting, “Theory of a Boundary Layer,” Science, Moscow, 1974.
- L. D. Landau and E. M. Lifshits, “Hydrodynamics,” Science, Moscow, 1986.
- I. E. Idelchik, “Hand-Book of Hydraulic Resistances,” Mechanical Engineering, Moscow, 1992.
- J. K. Batchelor, “An Introduction to Fluid Dynamics,” NIC, Moscow-Izhevsk, 2004.
- L. D. Landau and E. M. Lifshits, “The Theory Elasticity,” Science, Moscow, 1987.
- J. O. Hinze, “Turbulence. An Introduction to Its Mechanism and Theory,” M3Graw-Hill Book Company, Inc., New York, 1959.
- A. S. Monin and A. M. Jaglom, “Statistical Hydromechanics,” Science, Moscow, 1967.

