Engineering
Vol. 2 No. 10 (2010) , Article ID: 3181 , 7 pages DOI:10.4236/eng.2010.210104
Nonlinear Control of an Induction Motor Using a Reduced-Order Extended Sliding Mode Observer for Rotor Flux and Speed Sensorless Estimation
1Département Génie Electrique et Electronique, Institut National Polytechnique Houphouët Boigny
(INP HB), BP 1093 Yamoussoukro Côte d’Ivoire
2Université de Lyon, AMPERE, INSA Lyon, CNRS UMR 5005, Villeurbanne 69621, France
E-mail: abakaci@yahoo.fr
Received July 13, 2010; revised August 19, 2010; accepted August 21, 2010
Keywords: Robust Nonlinear Control, Induction Motor, Reduced-Order Extended Sliding Mode Observers, Parameter Estimation
ABSTRACT
This article proposes an innovative strategy to the problem of non-linear estimation of states for electrical machine systems. This method allows the estimation of variables that are difficult to access or that are simply impossible to measure. Thus, as compared with a full-order sliding mode observer, in order to reduce the execution time of the estimation, a reduced-order discrete-time Extended sliding mode observer is proposed for on-line estimation of rotor flux, speed and rotor resistance in an induction motor using a robust feedback linearization control. Simulations results on Matlab-Simulink environment for a 1.8 kW induction motor are presented to prove the effectiveness and high robustness of the proposed nonlinear control and observer against modeling uncertainty and measure-ment noise.
1. Introduction
The induction motors (IM) become very popular for motion control applications due to its reasonable cost, simple and reliable construction. However, the control of IM is proved very difficult since the dynamic systems are non linear, the electric rotor variables are not usually measurable or the transducers are expensive (such as torque, seed, flux transducers) and the physical parameters are often imprecisely known or variable. For instance, the rotor resistance drifts with the temperature of the rotor current frequency.
This naturally structure of non-linear and multivariable state of IM models induces the use of the non-linear control methods and in particular the robust feedback linearization strategy [1-3] to permit a decoupling, assure a good dynamic performance and stability of the IM.
However, a variation of the rotor resistance can induce a state-space “coupling” which can induce a degradation of the system. In order to achieve better dynamic performance, an on-line estimation of rotor fluxes, speed and rotor resistance is necessary. An approach proposed in [4,5] to estimate with success the state variables in an IM is the use of the full-order Sliding Mode Observer (SMO). This latter, built from the dynamic model of the IM by adding corrector gains with switching terms, is used to provide not only the unmeasurable state variable estimation (rotor fluxes and speed) but also the estimation of the measurable parameters (stator currents). However the determination of the measurable parameters estimation imposes some estimation algorithms very long and usually sophisticated with an increase of the computational volume. Therefore, in order to reduce the accuracy and the computation rate of the estimation algorithms, the measured parameters estimation is not necessary.
Thus a Reduced-Order Discrete-Time Extended Sliding Mode Observer (RDESMO) for the IM is presented in this paper to solve only and specially the problem of the unmeasurable parameters estimation (rotor fluxes, speed and rotor time constant).
So after a brief review of the IM model, a robust input-output linearization and decoupling control of induction motor is presented in Section 2. A reduced-order discrete-time Extended Sliding Mode Observer (ESMO) is developed in Section 3. Section 4 describes the simulation results carried out on a 1.8 kW IM drive system. Finally, conclusions are summarized in Section 5.
2. Induction Motor Model and Robust Feedback Control
By assuming that the saturation of the magnetic parts and the hysteresis phenomenon are neglected, the classical dynamic model of the IM in a (d, q) synchronous reference frame can be described by [6]:

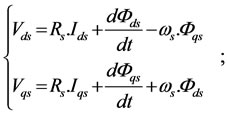 (1.a)
(1.a)
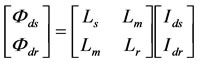 ;
;  (1.b)
(1.b)
The load mechanical equation is:
 (1.c)
(1.c)
The application of (1.a) to (1.c) returns a system of fifth-order non-linear differential equation, with as state variables the stator currents (Ids, Iqs), the rotor fluxes (Fdr, Fqr) and the rotor pulsation (wr):
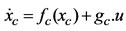 where xc = [Ids Iqs Fdr Fqr wr ]t, u = [Vds Vqs]t
where xc = [Ids Iqs Fdr Fqr wr ]t, u = [Vds Vqs]t
 (2)
(2)
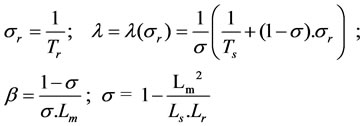
Moreover, by choosing a rotating reference frame (d, q) so that the direction of axe d is always coincident with the direction of the rotor flux representative vector (field orientation), it is well known that this rotor field orientation in a rotating synchronous reference frame realizes:
Fdr = Fr = Constant and Fqr = 0 (3)
Thus the dynamic model of the IM, completed with the output equation, can be rewritten as:
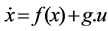 ; y =[h1(x) h2(x)]t = [Fr wr ]t with
; y =[h1(x) h2(x)]t = [Fr wr ]t with
x = [Ids Iqs Fr wr ]t, u = [Vds Vqs]t
 (4)
(4)
From the expressions (2) and (3), one can write:
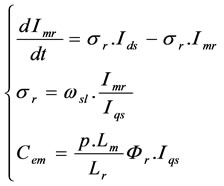 with
with 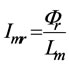 (5)
(5)
This relation (5) shows that the dynamic model of the IM can be represented as a non-linear function of the rotor time constant. A variation of this parameter can induce, for the IM, a lack of field orientation, performance and stability. Thus, to preserve the reliability, robustness performance and stability of the system under parameters variation (in particular the rotor time constant variations) and disturbances, we can uses a robust feedback linearization strategy to regulate the motor states.
As a matter of fact, we can see that the system (4) has relative degree r1 = r2 = 2 and can be transformed into a linear and controllable system by chosen [7]:
• a suitable change of coordinates given by:
z1 = h1(x); z2 = Lf h1(x); z3 = h2(x);
z4 = Lf h2(x);
• the feedback linearization control having the following form:
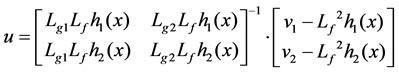
where v1 and v2 are the new inputs of the obtained decoupled systems
• and two robust controllers C(s) to provide a good regulation and convergence of the rotor flux (Fr ) and speed (wr). On the other hand, in order to impose after a closed loop a second order dynamic behaviour defined by H(s), the controller C(s) can be chosen by [8]:
 (6)
(6)
where the real t0 is an adjusting positive parameter.
The block diagram structure for the control of (Fr, wr) is as follows:

Furthermore, as the control of an IM generally required the knowledge of the instantaneous flux of the rotor that is not measurable, a full-order SMO built from the model (2) by adding corrector gains with switching terms is widely used [7,9] with success for on-line estimation at one and the same time of rotor time constant, fluxes, currents or speed. The equivalent value of the switching function depends on the current errors given by the difference between the estimated currents to their real or measured values. However, as the currents are already measurable, their estimated values are not therefore necessary.
Thus in the next section, in order to reduce the execution time of the observation with respect to the rotor time constant variations, a RDESMO is proposed to provide only the unmeasurable parameters estimation (rotor fluxes, rotor time constant and speed). And the switching term of this reduced observer will be only function of the measurable parameters (voltage, currents…).
3. Reduced-Order Discrete-Time Extended Sliding Mode Observer
3.1 Reduced-Order Sliding Mode Observer
Let us consider the dynamic model of the IM given by the system (2). Assume that among the state variable, the stator currents (Ids, Iqs) are measurable, therefore their on-line estimation is not necessary. Thus from the expression (2), in order to estimate only the rotor flux (Fdr, Fqr) and speed (wr), a reduced dimensional state vector defined by Xr= [Fdr Fqr wr]T =[x1 x2 x3], T can be introduced. The corresponding reduced-order state space equation becomes:
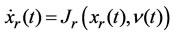
Where n(t) = [Ids, Iqs]T is the new input.
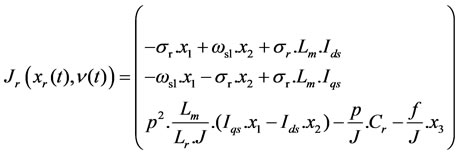 (7)
(7)
The fact that the state vector only consists of the rotor flux and speed offers an advantage namely the reduction of the computational volume and complexity. Thus the rotor flux and speed can be more easily and rapidly estimated. Denote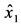 ,
,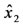 and
and  the estimates of the fluxes Fdr, Fqr and wr. The Reduced-order SMO is a copy of the model (7) by adding corrector gains with switching terms:
the estimates of the fluxes Fdr, Fqr and wr. The Reduced-order SMO is a copy of the model (7) by adding corrector gains with switching terms:
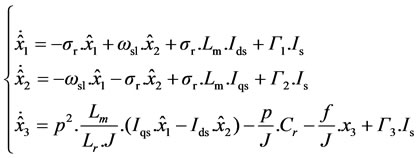 (8)
(8)
where G1, G2 and G3 are the observer gains. The switching “Is” is defined as
 (9)
(9)
where 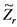 is a function depending on the parameters measurements (stator currents, voltages…).
is a function depending on the parameters measurements (stator currents, voltages…).
Setting  , the estimation error dynamics is given by:
, the estimation error dynamics is given by:
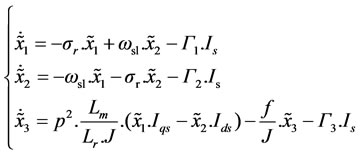 (10)
(10)
With the following observer gain matrices given by the expression (11), the estimation error 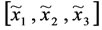 converges to zero.
converges to zero.
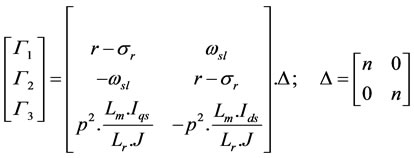 (11)
(11)
where r and n are positive adjusting parameters which play a critical role in the stability and the velocity of the observer convergence.
3.2. Reduced-Order Extended Sliding Mode Observer
In order to estimate the rotor time constant, a reduced dimensional extended state vector defined by Xre = [Fdr Fqr wr sr]T =[x1 x2 x3 x4] T has been introduced with sr = Rr/Lr. The corresponding reduced-order extended state space equation becomes:  where
where
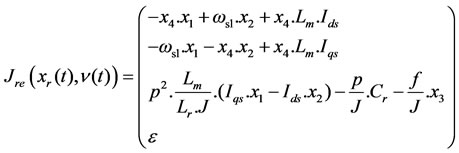 (12)
(12)
where e presents the slow variation of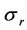 . The proposed Reduced-order ESMO is:
. The proposed Reduced-order ESMO is:
 (13)
(13)
where is, G1, G2 and G3 are respectively defined by (9) and (11).
To determine observer gain G4, it can be supposed that the observation errors of the fluxes converge to zero. The estimation errors of the fluxes 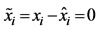 (i = 1,2) are then given by:
(i = 1,2) are then given by:
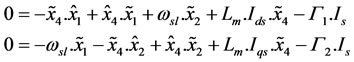 (14)
(14)
By replacing the expressions of 1 and 2 in (14), the estimation error dynamics of the rotor time constant is given by:
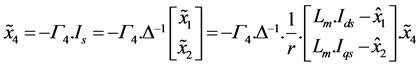
We can see that this error dynamics is locally and exponentially stable by chosen:
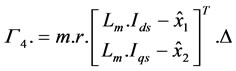 with m > 0 (15)
with m > 0 (15)
The parameter m is adjusted with respect to rotor time constant estimation.
Finally, from the expressions (11) and (15), it can be seen that there are three positive adjusting gains: r, n and m which play a critical role in the stability and the velocity of the observer convergence. These three adjusting parameters must be chosen so that the reduced observer satisfies robustness properties, global or local stability, good accuracy and considerable rapidity.
In order to implement the reduced-order ESMO algorithm in a DSP for real-time applications, the corresponding reduced-dimension state space equation defined in (12) must be discretized using Euler approximation (1st order). Thus the new discrete-time varying model represented by a function depending on the stator current is given by:

with
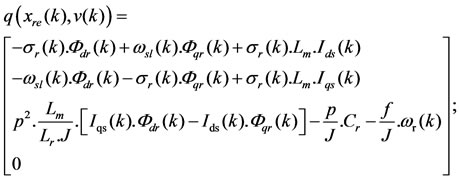 (16)
(16)
where k means the kth sampling time, i.e. t = k.Te with Te the adequate sampling period chosen without failing the stability and the accuracy of the discrete-time model.
The proposed RDESMO can be defined by the following equation:
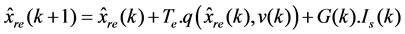 (17)
(17)
where the prediction vector is:
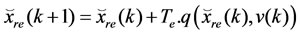
with 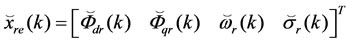
The switching vector Is(k), deduced from the continuous case given by (9), can be written as:
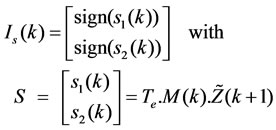 (18)
(18)
where
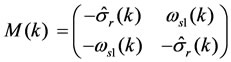 ,
,
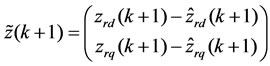
Let us introduce the measure vector zr(k+1) = [zrd(k+1), zrq(k+1)]T written as follows:
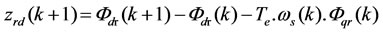 and
and
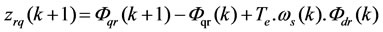
From the electrical Equation (1.a) of the IM, an approximate (1st order) discrete-time relation of the fluxes is given by:
 and
and
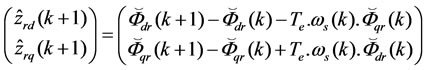 (19)
(19)
The proposed gain matrix representation G(k), deduced from the continuous case given by (11) and (15)can be defined as follows (discrete-time approach):
 (20)
(20)
Once the fluxes are estimated, it is easy to deduce the estimated torque defined by:
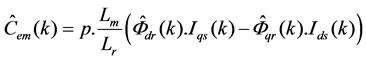 (21)
(21)
4. Simulation Results
In order to verify the feasibility of the proposed RDESMO, the simulation on SIMULINK from Mathwork has been carried out for a 1.8 kW induction motor controlled with a robust linearization via feedback algorithm (Figure 1). The nominal parameters of the induction motor are given in the Table 1.
The RDESMO is implanted in a S_function using C language. In order to evaluate its performances and effectiveness, the comparisons between the observed state variables and the simulated ones have been realized for several operating conditions with the presence of about 15% noise on the simulated currents (Ids, Iqs) or speed. Thus, using a sampling period Te = 1 ms, the simulations are realized at first in the nominal case with the nominal parameters of the induction motor (Table 1) and then, in the second case, with 50% variation of the nominal rotor time constant (sr = 1.5 srn) in order to verify the rotor time constant tracking and flux estimation.
Figure 2 and Figure 3 show the simulation results for a step input of the rotor speed and flux. One can see that in both nominal (Figures 2(a), 2(c)) or non-nominal (Figures 3(a’), 3(c’)) cases, the estimated values of fluxes and torque converge very well to their simulated values.
The observed fluxes (Figure 2(a)) indicate the good orientation (Fdr is constant and Fqr converges to zero) which is due to a favorable rotor time constant estimation (Figures 2(b), 3(b’)). The estimated torque (Figure 2(c)) is in good agreement with the simulated value.
Once the fluxes are estimated, we can deduce the algorithm of the feedback linearization control (Figure 1). The waveforms show the good uncoupling between the rotor flux and the speed because a step variation in Fdr (Figure 2(a) and Figure 3(a’)) can not generate a speed r change (Figure 2(d) and Figure 3(d’)). Thus the field orientation and the synthesis of robust linearization and decoupling control are well verified.
All those results show the satisfying tuning, the excellent performance of the robust decoupling control and RDESMO against rotor resistance variations and perturbations or noises.
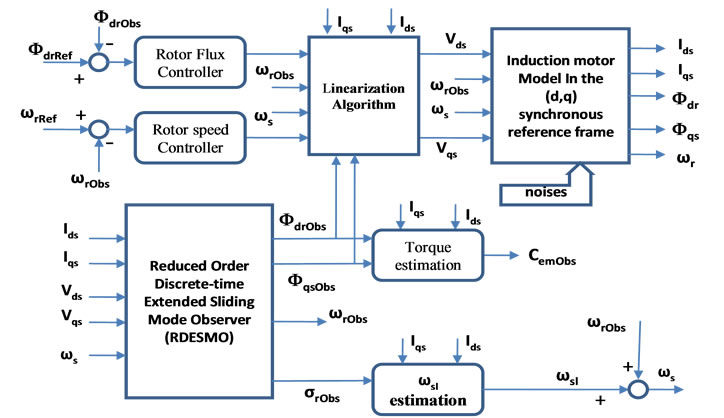
Figure 1. Simulation scheme of the system.
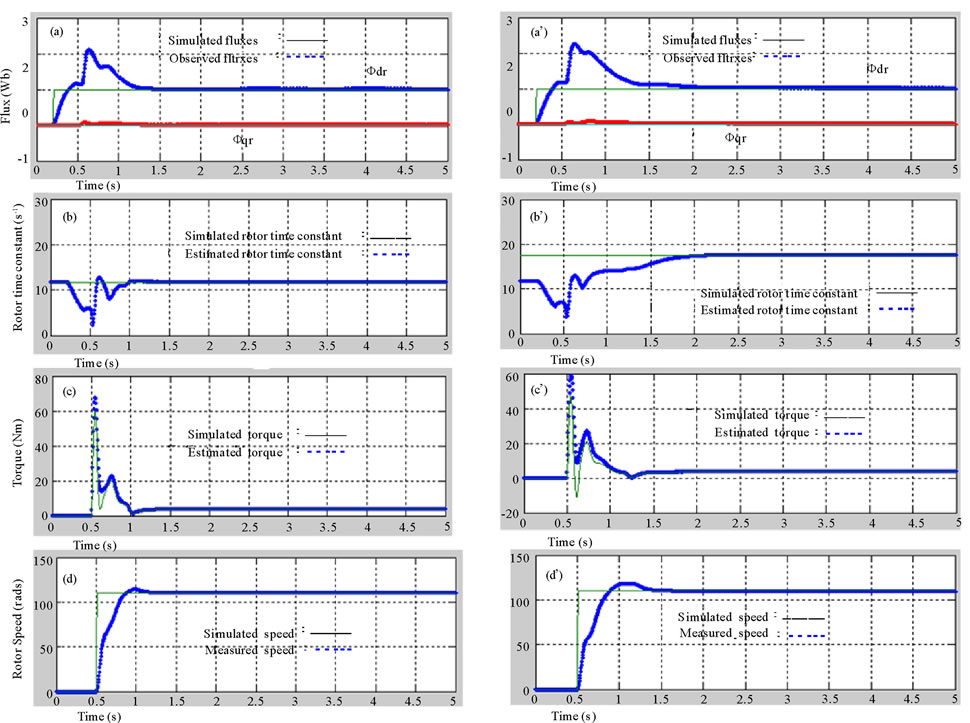
Figure 2. (a, b, c, d): Nominal case (Rr = Rrn).
Figure 3. (a’, b’, c’, d’): Non nominal case (Rr = 1.5Rrn).

Table 1. Nominal parameters of the induction motor.
5. Conclusions
We have shown in this paper that a robust feedback linearization strategy and RDESMO are used to permit a regulation and observation for the Induction motor states in order to assure a good dynamic performance and stability of the global system. In order to reduce the observation execution time, this RDESMO, based on the full -order SMO principle, permit only and specially for the reconstruction of the parameters non measurable in an IM (the fluxes, speed and the rotor time constant estimation).
The interesting simulation results obtained on the induction motor show the effectiveness, the convergence and the stability of this robust decoupling control and RDESMO against rotor resistance variations, measured noises and load. Thus, in order to validate the robustness of this non-linear control and RDESMO, Experimental results on a testing bench for a 1.8 kW induction motor will be present in the next research project.
6. REFERENCES
- D. I. Krein, I. J. Ha and M. S. Ko, “Control of Induction Motors via Feedback Linearization with Input-Output Decoupling,” International Journal of Control, Vol. 51, No. 4, 1989, p. 863-883.
- K. B. Mohanty, N. K. De and A. Routray, “Sensorless Control of a Linearized and Decoupled Induction Motor Drive,” National Power Systems Conference, NPSC, Kharagpur, India, December 2002, pp. 46-49.
- R. Yazdanpanah, J. Soltani and G. R. A. Markadeh, “Nonlinear Torque and Stator Flux Controller for Induction Motor Drive Based on Adaptive Input-Output Feedback Linearization and Sliding Mode Control,” Energy Conversion and management, Vol. 49, No. 4, 2008, pp. 541-550.
- P. A. Bogdan and A. Keyhani, “Sliding-Mode Flux Observer with Online Rotor Parameter Estimation for Induction Motors,” IEEE Transactions on Industrial Electronics, Vol. 54, No. 2, April 2007, pp. 716-723.
- A. Derdiyok, “Speed-Sensorless Control of Induction Motor Using a Continuous Control Approach of Sliding-Mode and Flux Observer,” IEEE Transactions on Industrial Electronics, Vol. 52, No. 4, August 2005, pp. 1170-1176.
- D. F. Bernard and L. Jean-Paul, “Identification et observation des actionneurs électriques,” Vol. 1 & 2, Hermes, Paris, 2007.
- O. Asseu, Z. Yeo, M. Koffi, X. Lin-Shi, C. T. Haba and G. L. Loum, “Robust Decoupling Control and Extended Sliding Mode Observer for an Induction Motor,” News -Phys Chem, Vol. 48, July 2009, pp. 1-8.
- J. C. Doyle, B. A. Francis and A. R. Tannenbaum, “Feedback Control Theory,” Maxwell MacMillan Internat, New York, 1992.
- M. Tursini, R. Petrella and F. Parasiliti, “Adaptive Sliding Mode Observer for Speed Sensorless Control of Induction Motors,” IEEE Transactions on Industry Applications, Vol. 36, No. 5, September/October 2000, pp. 1380 -1387.
Nomenclature
Cem, Cl : Electromagnetic and load torques, N.m.
f : friction coefficient, Nm.s/rad.
Ids, Iqs, Imr: Stationary frame (d,q)-axis stator currents and rotor magnetizing current, A.
J: inertia, kg.m2.
Lr, Ls, Lm, Lf : rotor, stator, mutual and leakage inductances, H.
p: pole pair number.
Rs, Rr : stator and rotor referred resistance, W.
Te, Tr, Ts : sampling period, rotor and stator time constant (Tr = Lr/Rr = 1/σr; Ts = Ls/Rs), s.
Vds, Vqs : Stationary frame dand q-axis stator voltage, V.
Fdr, Fqr: d-q components of rotor fluxes, Wb.
Fds, Fqs: d-q components of stator fluxes, Wb.
ws, wr, wsl : stator, rotor and slip pulsation (or speed), rad/s.

