Intelligent Control and Automation
Vol.5 No.3(2014), Article
ID:48605,10
pages
DOI:10.4236/ica.2014.53017
Constructive General Bounded Integral Control
Baishun Liu
Academy of Naval Submarine, Qingdao, China
Email: baishunliu@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 June 2014; revised 5 July 2014; accepted 15 July 2014
ABSTRACT
This note proposes a systematic and more generic method to construct general bounded integral control. It is established by defining three new function sets and citing two function sets to construct three kinds of general bounded integral control actions and integrators, resorting to a universal strategy to transform ordinary control into general integral control and adopting Lyapunov method to analyze the stability of the closed-loop system. A universal theorem to ensure regionally as well as semi-globally asymptotic stability is provided in terms of some bounded information, and even does not need exact knowledge of Lyapunov function. Its one feature is that the indispensable element used to construct the general integrator can be taken as any integrable function, which satisfies Lipschitz condition and the self excited integral dynamic is asymptotically stable. Another feature is that the method to construct general bounded integral control action is extended to a wider function set. Based on this method, the control engineers not only can choose the most appropriate control law in hand but also have more freedom to construct the bounded integral control actions and integrators, and then a high performance integral controller is more easily found. As a result, the generalization of the bounded integral control is achieved.
Keywords:General Integral Control, Nonlinear Control, Bounded Integral Control, General Nonlinear Integrator, Output Regulation

1. Introduction
In 2009, the idea of general integral control, which uses all available state variables to design the integrator, firstly was proposed by [1] , which presented some general integrators and controllers. However, their justification was not verified by mathematical analysis. In 2012, general integral control design based on linear system theory was presented by [2] , where the linear combination of all the states of dynamics was used as the integrator.
The results, however, were local. The regional as well as semi-global results were proposed in [3] , where the sliding mode manifold was used as the integrator, and then general integral control design was achieved by using sliding mode technique and linear system theory. In 2013, a class of nonlinear integrator, which was shaped by diffeomorphism, was proposed by [4] , where feedback linearization technique was used to analyze the closed-loop system stability. General concave integral control was proposed in [5] , where a class of concave function gain integrator is presented and the partial derivative of Lyapunov function is introduced into the integrator design. In consideration of the twinning of the concave and convex concepts, general convex integral control was proposed by [6] , where the method to design the convex function gain integrator is presented and its highlight point is that the integral control action seems to be infinity but its factually is finite in time domain. Although general concave and convex integral control are all bounded integral control, one major limitation of them is that the indispensable element of the integrator is limited to the partial derivative of Lyapunov function, another is the function sets, which are used to design the general concave and convex integrator and integral control action, only were limited to two kinds of function sets. These two limitations become a serious obstruction to design a high performance integral controller. In addition, the generalization of the integrator and integral control action, which is achieved by defining two function sets, respectively, was proposed by [7] , and its one drawback is that the integral control action could tend to infinity.
In consideration of the limitation of general concave and convex integral control, the aim of this paper is to propose a systematic and more generic method to construct general bounded integral control such that for a particular application, the control engineers not only can choose the most appropriate control law in hand but also have more freedom to construct the bounded integral control action and integrator. The main contributions are as follows: 1) three new function sets are defined, respectively; 2) three kinds of method to construct general bounded integral control action and integrator are proposed; 3) the indispensable element used to construct the integrator is not confined to the partial derivative of Lyapunov function [5] [6] and function set [7] , which is used to construct the integrator, and can be taken as any integrable function, which satisfies Lipschitz condition and the self excited integral dynamic is asymptotically stable; 4) the function sets used to construct the bounded integral control action have a wider range of choice than the corresponding function sets proposed by [5] -[7] ; 5) a class of positive define bounded gain function is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the control performance; 6) exact knowledge of Lyapunov function is not necessary and it only needs to satisfy some bounded information; 7) by using Lyapunov method and LaSalle’s invariance principle, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. As a result, the generalization of the bounded integral control is achieved.
Throughout this paper, we use the notation
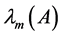 and
and
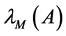 to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix
to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix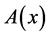 , for any
, for any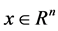 . The norm of vector
. The norm of vector
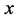 is defined as
is defined as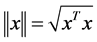 , and that of matrix
, and that of matrix
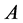 is defined as the corresponding induced norm
is defined as the corresponding induced norm
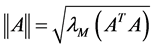 .
.
The remainder of the paper is organized as follows. Section 2 describes the system under consideration, assumption, definition and proof of Lemma. Section 3 addresses the method to construct general bounded integral control. Conclusions are presented in Section 4.
2. Problem Formulation
Consider the following nonlinear system,
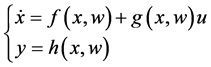 (1)
(1)
where
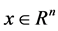 is the state,
is the state,
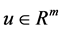 is the control input,
is the control input,
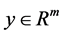 is the controlled output,
is the controlled output,
 is a vector of unknown constant parameters and disturbances. The function
is a vector of unknown constant parameters and disturbances. The function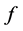 ,
,
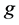 and
and
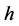 are continuous in
are continuous in
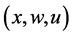 on the whole control domain
on the whole control domain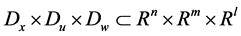 . Let
. Let
 be a vector of constant reference. Set
be a vector of constant reference. Set
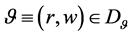 and
and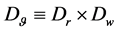 . We want to design a feedback control law
. We want to design a feedback control law
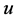 such that
such that
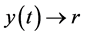 as
as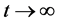 .
.
Assumption 1: For each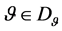 , there is a unique pair
, there is a unique pair
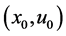 that depends continuously on
that depends continuously on
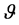 and satisfies the equations,
and satisfies the equations,
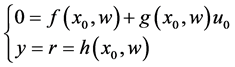 (2)
(2)
so that
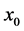 is the desired equilibrium point and
is the desired equilibrium point and
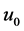 is the steady-state control that is needed to maintain equilibrium at
is the steady-state control that is needed to maintain equilibrium at , where
, where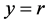 .
.
No loss of generality, we state all definitions, theorems and assumptions for the case when the equilibrium point is at the origin of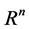 , that is,
, that is,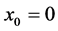 .
.
Assumption 2: No loss of generality, suppose that the function
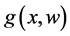 satisfies the following inequalities,
satisfies the following inequalities,
 (3)
(3)
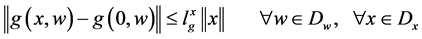 (4)
(4)
where
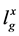 is a positive constant.
is a positive constant.
Assumption 3: Suppose that there exists a control law
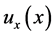 such that
such that
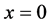 is an exponentially stable equilibrium point of the system (5) and the inequality (6) hold,
is an exponentially stable equilibrium point of the system (5) and the inequality (6) hold,
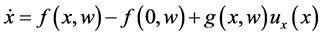 (5)
(5)
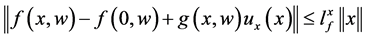 (6)
(6)
and there exists a Lyapunov function
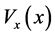 such that the following inequlities,
such that the following inequlities,
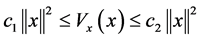 (7)
(7)
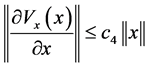 (8)
(8)
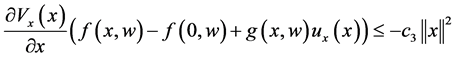 (9)
(9)
hold for all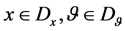 , where
, where
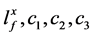 and
and
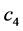 are all positive constants.
are all positive constants.
For the purpose of this paper, it is convenient to introduce the following definitions and Lemmas. For the convenient comparison with the general concave and convex integral control, it is necessary to explain that the following Definition 1 and 2 was proposed by reference [5] [6] , respectively.
Definition 1:
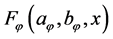 with
with
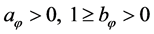 and
and
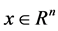 denotes the set of all continuous differential increasing bounded functions [5] [8] ,
denotes the set of all continuous differential increasing bounded functions [5] [8] ,
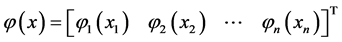
such that
 ,
,
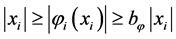 ,
,
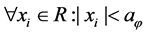
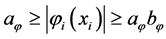 ,
,

 .
.
where
 stands for the absolute value.
stands for the absolute value.
Figure 1 depicts the region allowed for one component of functions belonging to function set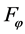 . For instance, for all
. For instance, for all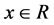 , hyperbolic tangent function, arc tangent function, Amosin function [8] and so on, all belong to function set
, hyperbolic tangent function, arc tangent function, Amosin function [8] and so on, all belong to function set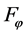 .
.
Definition 2:
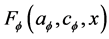 with
with
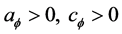 and
and , denotes the set of all continuous differential increasing functions [6] ,
, denotes the set of all continuous differential increasing functions [6] ,
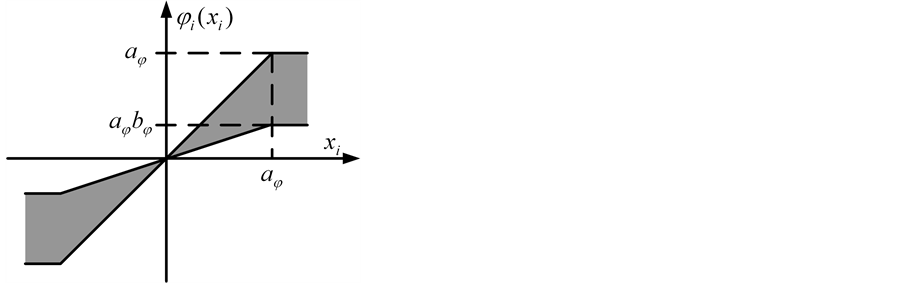
Figure 1. The region allowed for one component of functions belonging to function set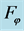 .
.
such that
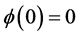 ,
,
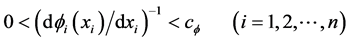
and given any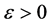 , there exists a positive constant
, there exists a positive constant
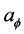 such that
such that
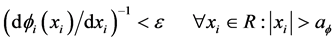 .
.
where
 stands for the absolute value.
stands for the absolute value.
Figure 2 describes an example curve and the region allowed for the derivative reciprocal of one component of functions belonging to function set . For instance, for all
. For instance, for all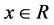 , the functions,
, the functions,
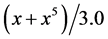 ,
,
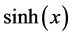 ,
,
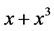 and so on, all belong to function set
and so on, all belong to function set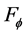 .
.
Definition 3:
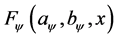 with
with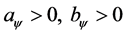 , and
, and
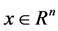 denotes the set of all continuous differential increasing functions,
denotes the set of all continuous differential increasing functions,
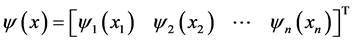
such that
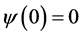 ,
,
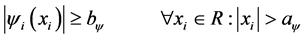
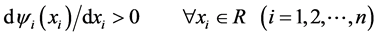 .
.
Figure 3 depicts the example curves for one component of functions belonging to function set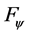 . For instance, for all
. For instance, for all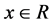 , the functions,
, the functions,
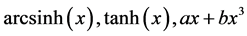 with
with
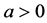 and
and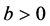 ,
,
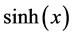 , and so on, all belong to function set
, and so on, all belong to function set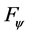 .
.
Definition 4:
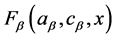 with
with
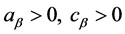 and
and
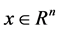 denotes the set of all continuous positive define bounded functions,
denotes the set of all continuous positive define bounded functions,
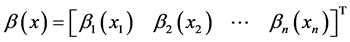
such that
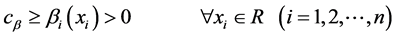 and given any
and given any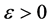 , there exists
, there exists
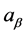 such that
such that
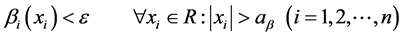 .
.
Figure 4 depicts the example curves and the region allowed for one component of functions belonging to
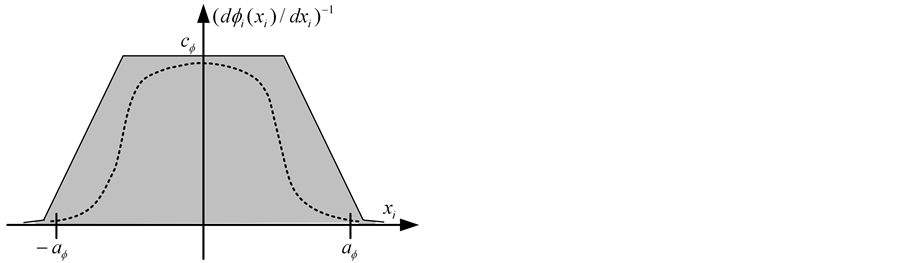
Figure 2. Example curve and the region allowed for the derivative reciprocal of one component of functions belonging to function set .
.
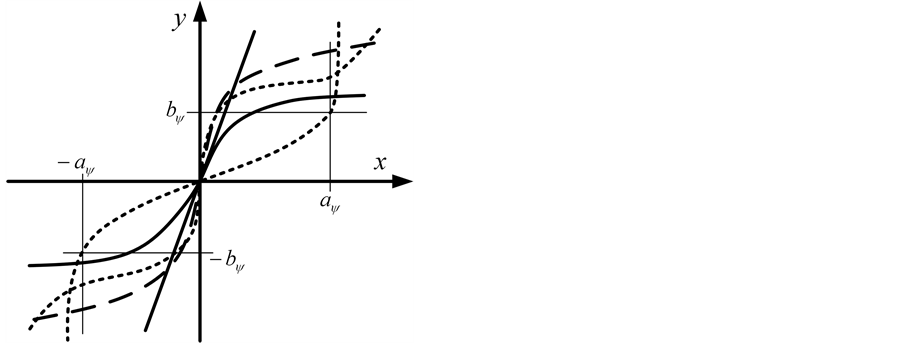
Figure 3. Example curves of functions belonging to function set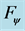 .
.
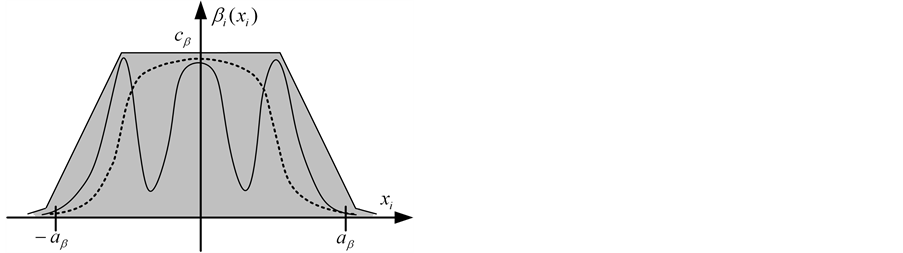
Figure 4. Example curves and the region allowed for one component of functions belonging to function set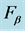 .
.
function set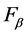 . For instance, for all
. For instance, for all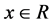 , the functions,
, the functions,
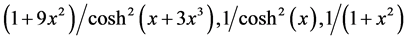 , and so on, all belong to function set
, and so on, all belong to function set .
.
Definition 5:
 with
with
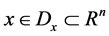 denotes the set of all integrable functions,
denotes the set of all integrable functions,
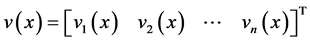
such that
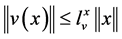 ,
,
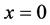 is an asymptotically stable equilibrium point of the self excited integral dynamic
is an asymptotically stable equilibrium point of the self excited integral dynamic
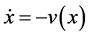 for all
for all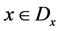 .
.
where
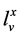 is a positive constant. For instance, for all
is a positive constant. For instance, for all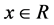 , the functions,
, the functions,
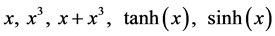 and so on, all belong to function set
and so on, all belong to function set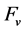 .
.
Lemma 1: Let
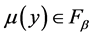 or
or
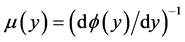 with
with
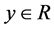 or
or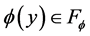 , and then the function [6] ,
, and then the function [6] ,
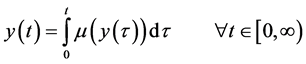
is a positive define bounded increasing function, that is,
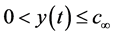 for all
for all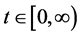 , where
, where
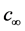 is the limit of
is the limit of
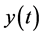 as
as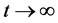 . Its proof consults the reference [6] .
. Its proof consults the reference [6] .
Lemma 2: Let
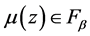 or
or
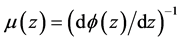 with
with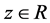 ,
,
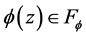 and
and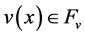 , and then the function,
, and then the function,
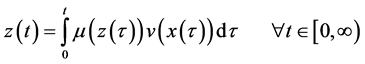
is bounded, that is,
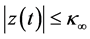 for all
for all
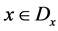 and
and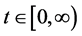 , where
, where
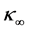 is a positive constant.
is a positive constant.
Proof: by definition of
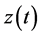 and Definition 5, we have,
and Definition 5, we have,
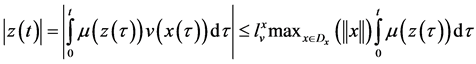
Now, using Lemma 1, we obtain,
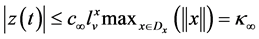 .
.
Thus,
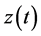 is bounded, that is,
is bounded, that is,
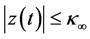 for all
for all
 and
and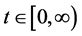 .
.
Discussion 1: Comparing the two function sets
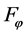 and
and
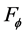 proposed by [5] [6] with the function set
proposed by [5] [6] with the function set , it is no hard to see that although they all claim that the function is continuous differential increasing function, the main differences are as follows: the limiting conditions of the function set
, it is no hard to see that although they all claim that the function is continuous differential increasing function, the main differences are as follows: the limiting conditions of the function set
 is less than the function sets
is less than the function sets
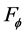 and
and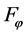 . Thus, the function set
. Thus, the function set
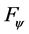 can completely includes the any functions belonging to the two function sets
can completely includes the any functions belonging to the two function sets
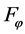 and
and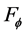 .
.
Discussion 2: Comparing the function set [7] , which was used to generalize the integral control action, with the function set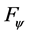 , the differences are the limiting condition about their derivatives, that is, the former demands
, the differences are the limiting condition about their derivatives, that is, the former demands
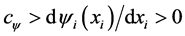 (
(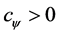 ,
,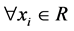 and
and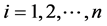 ). However, the latter only requires
). However, the latter only requires
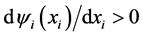 . Thus, the function set
. Thus, the function set
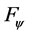 not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
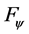 have a wider range of choice than the one proposed by [7] .
have a wider range of choice than the one proposed by [7] .
Discussion 3: Comparing the function set [7] , which was used to generalize the integrator, with the function set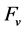 , the differences are that: the former is defined by resorting to Mean Value Theorem, therefore, it requires that the function is differential. However, the latter is defined by designing a self excited integral dynamic, and only demands its origin is asymptotically stable, and then differentiability condition is removed. Thus, it is not hard to see that the function set
, the differences are that: the former is defined by resorting to Mean Value Theorem, therefore, it requires that the function is differential. However, the latter is defined by designing a self excited integral dynamic, and only demands its origin is asymptotically stable, and then differentiability condition is removed. Thus, it is not hard to see that the function set
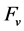 not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
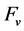 have a wider range of choice than the one proposed by [7] .
have a wider range of choice than the one proposed by [7] .
Discussion 4: It is obvious that the bound of function,
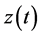 , which is obtained by Lemma 2, is too conservative and even is not of interest. The situation, however, is not as bad as it might seem. As shown by Figure 2 and Figure 3, we can use
, which is obtained by Lemma 2, is too conservative and even is not of interest. The situation, however, is not as bad as it might seem. As shown by Figure 2 and Figure 3, we can use
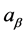 or
or
 as its approximate value in practice, corresponding to
as its approximate value in practice, corresponding to
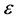 small enough.
small enough.
3. Constructive Method
In general, integral controller comprises three components: the stabilizing controller, integral control action and integrator. Thus, a general integral controller can be given as,
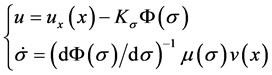 (10)
(10)
where
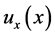 is an ordinary control law;
is an ordinary control law;
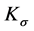 is a positive define diagonal matrix;
is a positive define diagonal matrix;
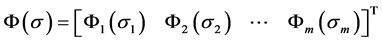 is a continuous differential increasing function with
is a continuous differential increasing function with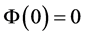 ;
;
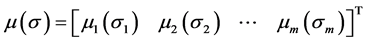 is a positive constant vector or positive define vector function;
is a positive constant vector or positive define vector function;
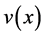 belongs to function set
belongs to function set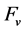 ;
;
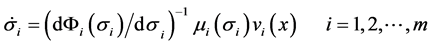 .
.
Thus, substituting (10) into (1), obtain,
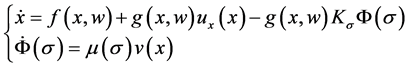 (11)
(11)
By Assumption 1 and choosing
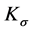 to be nonsingular and large enough, and then set
to be nonsingular and large enough, and then set
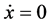 and
and
 of (11), obtain,
of (11), obtain,
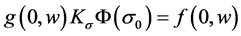 (12)
(12)
Therefore, we ensure that there is a unique solution,
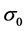 , and then
, and then
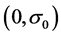 is a unique equilibrium point of the closed-loop system (11) in the control domain of interest. At the equilibrium point,
is a unique equilibrium point of the closed-loop system (11) in the control domain of interest. At the equilibrium point,
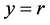 , irrespective of the value of
, irrespective of the value of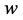 .
.
Now, the design task is to provide methods to construct the bounded integral control action and integrator in the control law (10) such that
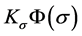 is bounded and
is bounded and
 is an asymptotically stable equilibrium point of the closed-loop system (11) in the control domain of interest. To achieve this objective, the methods can be summarized as follows:
is an asymptotically stable equilibrium point of the closed-loop system (11) in the control domain of interest. To achieve this objective, the methods can be summarized as follows:
Method 1: If we choose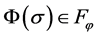 , and then by definition of
, and then by definition of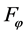 , it is easy to know that the integral control action is bounded for all
, it is easy to know that the integral control action is bounded for all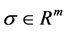 . Thus,
. Thus,
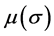 can be taken as any positive define bounded vector function or positive constant vector, that is,
can be taken as any positive define bounded vector function or positive constant vector, that is,
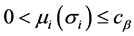 with
with
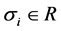 and
and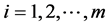 . Consequently, we have,
. Consequently, we have,
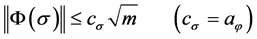 , and
, and
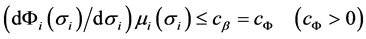 .
.
As a result, the generalization of the general concave integral control is achieved.
Method 2: If we choose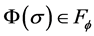 , and then design
, and then design
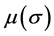 such that
such that
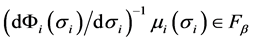 ,
,
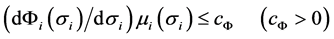 , and
, and
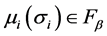
hold for all
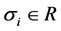 and
and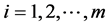 . Thus, by Lemma 1 and 2, it is easy to know that this kind of integral control action is bounded in time domain, that is,
. Thus, by Lemma 1 and 2, it is easy to know that this kind of integral control action is bounded in time domain, that is,
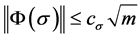
where
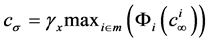 ,
,
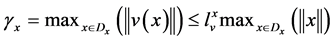 ,
,
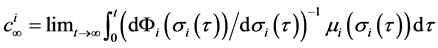 , and
, and
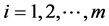 .
.
As a result, the generalization of the general convex integral control is achieved.
Method 3: If we choose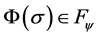 , constructive general bounded integral control can be divided into two cases: 1) if
, constructive general bounded integral control can be divided into two cases: 1) if
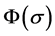 is bounded, and then
is bounded, and then
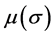 can be taken as any positive define bounded vector function or positive constant vector. The condition for
can be taken as any positive define bounded vector function or positive constant vector. The condition for
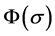 is the same as Method 1; 2) if
is the same as Method 1; 2) if
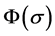 is unbounded for all
is unbounded for all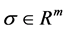 , and then
, and then
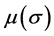 needs to be designed like Method 2. The condition for
needs to be designed like Method 2. The condition for
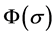 is the same as Method 2. It is obvious that this is a more generic method to construct general bounded integral control because the function set used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] . Moreover, it is worth noting that
is the same as Method 2. It is obvious that this is a more generic method to construct general bounded integral control because the function set used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] . Moreover, it is worth noting that
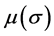 can be designed like Method 2 when
can be designed like Method 2 when
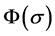 is bounded.
is bounded.
In addition, it is convenient to introduce the variable,
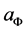 , which is equal to
, which is equal to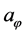 ,
,
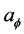 and
and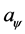 , respectively, corresponding to the above three kinds of choices of the function
, respectively, corresponding to the above three kinds of choices of the function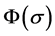 .
.
Based on the control law
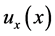 and three kinds of integral control actions and integrators above, the following theorem can be established.
and three kinds of integral control actions and integrators above, the following theorem can be established.
Theorem 1: Under Assumptions 1 - 3, if there exists a positive define diagonal matrix
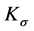 such that the following inequality,
such that the following inequality,
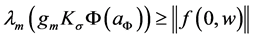 (13)
(13)
and the inequality (20) hold, and then
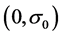 is an exponentially stable equilibrium point of the closed-loop system (11). Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
is an exponentially stable equilibrium point of the closed-loop system (11). Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
Proof: To carry out the stability analysis, we consider the following Lyapunov function candidate,
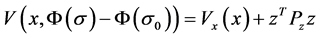 (14)
(14)
where
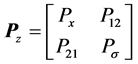 ,
,
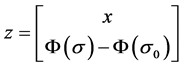 ,
,
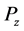 is a positive define
is a positive define
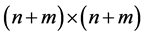 matrix;
matrix;
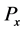 is a
is a
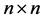 matrix;
matrix;
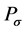 is a
is a
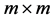 matrix;
matrix;
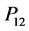 is a
is a
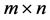 matrix,
matrix,
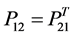 ,
,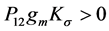 .
.
Obviously, Lyapunov function candidate (14) is positive define. Therefore, our task is to show that its time derivative along the trajectories of the closed-loop system (11) is negative define, which is given by,
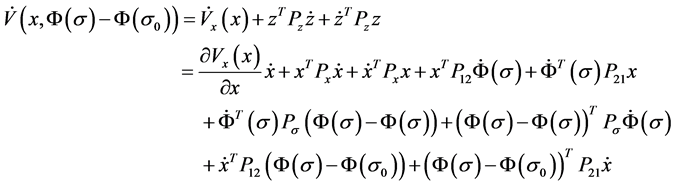 (15)
(15)
Substituting (12) into (11), we obtain,
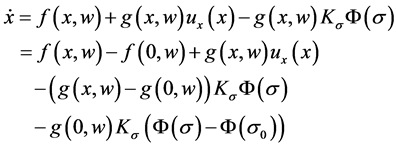 (16)
(16)
Now, by the above three kinds of choices of the function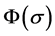 , we have,
, we have,
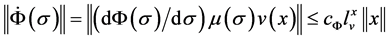 (17)
(17)
Substituting (16) into (15), and using (3), (4), (6), (8), (9), (17) and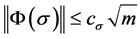 , we obtain,
, we obtain,
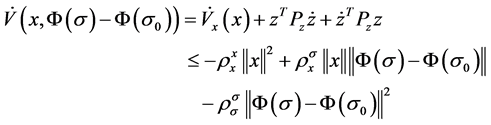 (18)
(18)
where
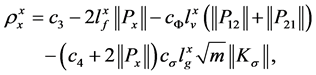
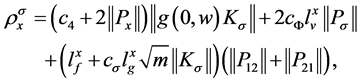 and
and
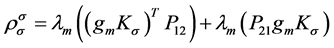 .
.
and then inequality (18) can be rewritten as,
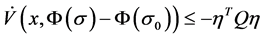 (19)
(19)
where
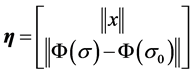 ,
,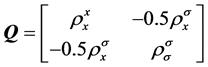 .
.
The right-hand side of the inequality (19) is a quadratic form, which is negative define when
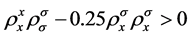 (20)
(20)
Using the fact that Lyapunov function (14) is a positive define function and its time derivative is a negative define function if the inequalities (13) and (20) hold, we conclude that the closed-loop system (11) is stable. In fact,
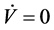 means
means
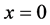 and
and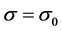 . By invoking LaSalle’s invariance principle [9] , it is easy to know that the closed-loop system (11) is asymptotically stable.
. By invoking LaSalle’s invariance principle [9] , it is easy to know that the closed-loop system (11) is asymptotically stable.
Discussion 5: Compared to general convex and concave integral control [5] [6] , it is easy to see that this paper is not a simple extension of them but proposes a systematic and more generic method to construct general bounded integral control. The main progresses are as follows: 1) the indispensable element
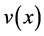 used to construct the integrator can be taken any functions belonging to function set
used to construct the integrator can be taken any functions belonging to function set
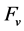 and is not confined to the partial derivative of Lyapunov function
and is not confined to the partial derivative of Lyapunov function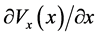 , which is used to construct the integrator in [5] [6] ; 2) a positive define bounded gain function
, which is used to construct the integrator in [5] [6] ; 2) a positive define bounded gain function
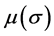 is introduced into the integrator, which can be used to improve the integral control performance; 3) a class of new function set
is introduced into the integrator, which can be used to improve the integral control performance; 3) a class of new function set
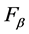 is defined, and then the method to construct general bounded integral control action and integrator is extended to a wider function set
is defined, and then the method to construct general bounded integral control action and integrator is extended to a wider function set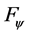 . As a result, this is a fire new and more generic method to construct general bounded integral control action and integrator; 4) we need not exact knowledge of Lyapunov function
. As a result, this is a fire new and more generic method to construct general bounded integral control action and integrator; 4) we need not exact knowledge of Lyapunov function
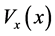 and only need it satisfy some bounded information. Moreover, if the partial derivative of Lyapunov function is attached into the function
and only need it satisfy some bounded information. Moreover, if the partial derivative of Lyapunov function is attached into the function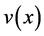 , the stability conditions can be relaxed. All these mean that the control engineers have more freedom to design the integrator and bounded integral control action, and then a high performance integral controller is more easily found.
, the stability conditions can be relaxed. All these mean that the control engineers have more freedom to design the integrator and bounded integral control action, and then a high performance integral controller is more easily found.
Discussion 6: Compared to the generalization integrator and integral control action proposed by [7] , the main differences are as follows: 1) the integrators proposed by [7] are unattached with the integral control action. However, the integrators presented here are all educed by differentiating the nonlinear function, which is used to produce the integral control action; 2) the integral control actions proposed by [7] could tend to infinity. However, the integral control actions proposed here are all bounded. This means that this kind of integral control can devote its mind to counteract the unknown constant uncertainties and filter out the other action, and then actuator saturation is easy to be removed in practice; 3) a positive define bounded gain function
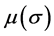 is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the integral control performance; 4) as mentioned at Discussion 2 and 3, the function sets
is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the integral control performance; 4) as mentioned at Discussion 2 and 3, the function sets
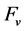 and
and
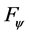 used to construct the integrator and integral control action, respectively, all have a wider range of choice than the corresponding function sets proposed by [7] .
used to construct the integrator and integral control action, respectively, all have a wider range of choice than the corresponding function sets proposed by [7] .
Remark 1: From the statement above, It is obvious that: First, five function sets for constructing general bounded integral control action is enumerated; Second, three general methods to construct the bounded integral control action are proposed; Final, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. Under the domination of this theorem, all of them synthesize a systematic and more generic method to construct general bounded integral control together. Consequently, for a particular application, the control engineers not only can choose the most appropriate control law in hand but also have more freedom to design the bounded integral control action and integrator, and then a high performance integral controller is more easily found.
4. Conclusion
This paper is not a simple extension of general convex and concave integral control but proposes a systematic and more generic method to construct general bounded integral control. The main contributions are as follows: 1) three new function sets are defined, respectively; 2) three kinds of method to construct general bounded integral control action and integrator are proposed; 3) the indispensable element used to construct the integrator is not confined to the partial derivative of Lyapunov function [5] [6] and function set [7] , which is used to construct the integrator, and can be taken as any integrable function, which satisfies Lipschitz condition and the self excited integral dynamic is asymptotically stable; 4) the function sets used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] ; 5) a class of positive define bounded gain function is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the control performance; 6) exact knowledge of Lyapunov function is not necessary and it only needs to satisfy some bounded information; 7) by using Lyapunov method and LaSalle’s invariance principle, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. As a result, the generalization of the bounded integral control is achieved.
References
- Liu, B.S. and Tian, B.L. (2009) General Integral Control. Proceedings of the International Conference on Advanced Computer Control, Singapore, 22-24 January 2009, 136-143. http://dx.doi.org/10.1109/ICACC.2009.30
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Linear System Theory. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3174-3177.
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Sliding Mode Technique. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3178-3181.
- Liu, B.S., Li, J.H. and Luo, X.Q. (2014) General Integral Control Design via Feedback Linearization. Intelligent Control and Automation, 5, 19-23. http://dx.doi.org/10.4236/ica.2014.51003
- Liu, B.S., Luo, X.Q. and Li, J.H. (2013) General Concave Integral Control. Intelligent Control and Automation, 4, 356-361. http://dx.doi.org/10.4236/ica.2013.44042
- Liu, B.S., Luo, X.Q. and Li, J.H. (accepted) General Convex Integral Control. International Journal of Automation and Computing.
- Liu, B.S. (submitted) On the Generalization of Integrator and Integral Control Action. International Journal of Modern Nonlinear Theory and Application.
- Kelly, R. (1998) Global Positioning of Robotic Manipulators via PD Control plus a Class of Nonlinear Integral Actions. IEEE Transactions on Automatic Control, 43, 934-938. http://dx.doi.org/10.1109/9.701091
- Khalil, H.K. (2007) Nonlinear Systems. 3rd Edition, Electronics Industry Publishing, Beijing, 126-128, 482-484.

