Intelligent Control and Automation
Vol.4 No.4(2013), Article ID:39506,6 pages DOI:10.4236/ica.2013.44047
Cuckoo Search for Solving Economic Dispatch Load Problem
Univ Estadual Paulista (UNESP/IGCE/DEMAC), Rio Claro, Brazil
Email: adriane@rc.unesp.br
Copyright © 2013 Adriane B. S. Serapião. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 20, 2013; revised July 20, 2013; accepted July 28, 2013
Keywords: Economic Dispatch Load; Cuckoo Search Algorithm; Swarm Intelligence; Optimization
ABSTRACT
Economic Load Dispatch (ELD) is a process of scheduling the required load demand among available generation units such that the fuel cost of operation is minimized. The ELD problem is formulated as a nonlinear constrained optimization problem with both equality and inequality constraints. In this paper, two test systems of the ELD problems are solved by adopting the Cuckoo Search (CS) Algorithm. A comparison of obtained simulation results by using the CS is carried out against six other swarm intelligence algorithms: Particle Swarm Optimization, Shuffled Frog Leaping Algorithm, Bacterial Foraging Optimization, Artificial Bee Colony, Harmony Search and Firefly Algorithm. The effectiveness of each swarm intelligence algorithm is demonstrated on a test system comprising three-generators and other containing six-generators. Results denote superiority of the Cuckoo Search Algorithm and confirm its potential to solve the ELD problem.
1. Introduction
The electrical systems are interconnected in order to obtain the benefits of minimum generation costs, maximum reliability and best operational conditions, such as sharing of power reserve, improving the stability and operating on emergency situations [1]. Thus, the optimization problem of the economic dispatch of electrical power is relevant to accomplish requirements of quality and efficiency in power generation.
The economic load dispatch is an issue in which it has generated units available and connected to the power system. During the operational activity of the system, it must comply the expected load (system’s demand), so that the sum of the power of the generating units is equal to the total load of the system and electrical losses.
The basic objective of the economic load dispatch problem of electrical power generation is the scaling of committed generating units outputs to find the consumer load demand at a minimal operating cost within a time interval (typically one hour), satisfying the inherent restrictions with the gathered generating units and the equality and inequality constraints imposed by the problem [2].
The economic dispatch for the operation of electrical groups is described as a multi-objective mathematical programming problem, where the goal is to minimize the function that determines the fuel cost (objective function), stating an optimal generation profile, subject to satisfaction of the energy load power and the technical limits of the operating groups.
The economic dispatch problem has complex and nonlinear characteristics, and usually with the presence of equality and inequality constraints. Several methods have been used to solve this problem since it was introduced, for example, iterative method, gradient based techniques, interior points method, linear programming and dynamic programming. However, the conventional approaches used for the optimization of this problem are inadequate, because the solution can be retained in traps of local minima [1]. Furthermore, the classical dispatch algorithms require incremental cost curves to be monotonically increasing/piecewise linear and some approximation should be made to satisfy the requirements. However, the input/output characteristics of modern generating units are inherently highly non-linear. Therefore, more interests have been focused on the application of Computational Intelligence (AI) methods for solving this kind of problem.
Some heuristic methods explore not only features of the problems but particularly also the analogy with other optimization methods found in nature. Such heuristics are called metaheuristics and are independent of the problem being treated. Many metaheuristics were proposed based on population for solving unconstrained optimization problems. Since population-based optimization techniques are more effective than the gradient techniques in finding the global minimum, they have been preferred in many applications, because metaheuristics approaches allow the insertion of constraints in a smoother manner.
Several models of the economic load dispatch problem using population-based methods have also been addressed in some works of literature, including the use of methods such as Genetic Algorithms [2], Particle Swarm Optimization [3,4], Evolutionary Programming [5], Bacterial Foraging Optimization (BFO) [6], Ant Colony Optimization [7], Harmony Search [8], Biogeographybased Optimization [9] and Seeker Optimization Algorithm [10].
The fundamental principle of these algorithms, also referred to as bioinspired methods, uses a constructive method for obtaining the initial population (initial feasible solutions represented by individuals) and a local search technique to improve the solution within the population, whereas the individuals (solutions) of population are evolved according to specified rules that consider the exchange of information among individuals. This process drives the population towards obtaining an optimal solution. Such algorithms are also known as swarm intelligence algorithms [11].
This paper applies the recent Cuckoo Search (CS) algorithm [12] to solve the economic load dispatch problem. Our motivation for using this population-based algorithm is due to two primary reasons highlighted by its authors for a superior performance of this algorithm in contrast with others metaheuristics, as discussed in [12]: a fine balance of randomization and intensification, and less number of control parameters. First, for any metaheuristic algorithm, a good balance of intensive local search strategy and an efficient exploration of the whole search space will usually lead to a more efficient algorithm. So, the success or failure of a population-based algorithms depends on its ability to establish proper tradeoff between exploration and exploitation. Random walk via Lévy flight used by CS is more efficient in exploring the search space as its step length is heavy-tailed, and any large step is possible. On the other hand, CS has some sort of elitism and/or selection similar to that used in Harmony Search. Second, there are just two parameters to be fine-tuned in CS algorithm: population size and discovery probability (pa). The CS convergence rate is insensitive to the parameter pa. This also means that it is not necessary to fine tune these parameters for a specific problem.
The effectiveness of this algorithm is demonstrated for test cases of three and six-generating units. The CS results are compared to six others population-based methods: Particle Swarm Optimization (PSO) [13], Shuffled Frog Leaping Algorithm (SFLA) [14], Bacterial Foraging Optimization (BFO) [15], Artificial Bee Colony (ABC) [16], Harmony Search (HS) [17] and Firefly Algorithm (FA) [18].
The remaining sections of this work are organized as follows: Section 2 describes the formulation of an ELD. Section 3 describes the CS algorithm. Section 4 presents the two case tests, the computational settings and analyzes the CS results when applied to case studies of ELDs with three and six-generating units and compared with the others six algorithms’ results. Lastly, Section 5 outlines the conclusions.
2. Problem Formulation
The purpose of the economic load dispatch problem in electrical power system is to schedule the outputs of committed generating units to meet the consumer load demand at a minimal operating cost, satisfying the equality and inequality constraints imposed to the system.
The economic dispatch for the operation of electrical units is described by a multi-objective mathematical programming problem, which consists of minimizing the function that determines the fuel cost (objective function), finding an optimal generation profile, subject to satisfy the load power and the technical limits of operation of the groups.
Consider an electrical groups park with n generating units. The total fuel cost for power generation to be minimized is the sum of contributions of each generating units, which is given by:
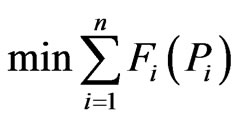 (1)
(1)
where: Fi is the fuel cost function for the generation unit i (in $/h) and Pi (in MW) is the real power output for this unit.
The fuel cost characteristics of each generation unit i is represented by a quadratic equation:
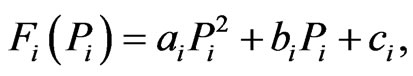 (2)
(2)
subject to:
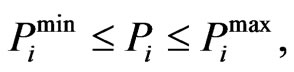 (3)
(3)
where: ai, bi and ci are the fuel cost coefficients of the unit i, and 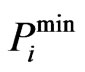 and
and 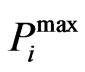 are the minimum and maximum generation limits of the real power of unit i (in MW).
are the minimum and maximum generation limits of the real power of unit i (in MW).
In this context, an equality constraint should be attempted. The total generated power by the units must be equal to the sum of total load demand and total real power loss in the transmission lines, as follows:
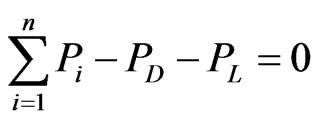 (4)
(4)
where: PD is the total system real power demand (in MW); PL is the overall system real power losses (in MW).
In the methodology of constant loss formula coefficients (loss coefficient method) or B-coefficients, the network losses are expressed as a quadratic function of the generators power outputs that can be approximated in the form:
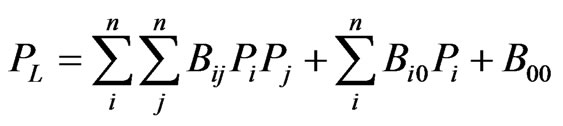 (5)
(5)
where: Bij are the elements of loss coefficient square matrix B, Bi0 is the i-th elements of the loss coefficient vector and B00 is the loss coefficient constant.
The generation capacity inequality constraint related to real power generation limits of each unit is given by Equation (3), whereas the power balance equality constraint (i.e., balance between demand and production) is represented by Equation (4).
The swarm optimization algorithms were applied to minimize the following objective function:
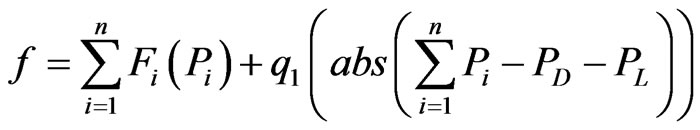 (6)
(6)
where: q1 is a positive constant to penalize the solutions that does not attend the power load balance.
This objective function was established to include not only the load distribution in the generating units with a lower cost but also to satisfy the equality constraint of the system.
3. Cuckoo Search Algorithm
Cuckoo search (CS) is inspired by some species of a bird family called cuckoo because of their special lifestyle and aggressive reproduction strategy. This algorithm was proposed by Yang and Deb [12]. The CS is an optimization algorithm based on the brood parasitism of cuckoo species by laying their eggs in the communal nests of other host birds, though they may remove others’ eggs to increase the hatching probability of their own eggs. Some host birds do not behave friendly against intruders and engage in direct conflict with them. If a host bird discovers the eggs are not their own, it will either throw these foreign eggs away or simply abandon its nest and build a new nest elsewhere [19].
The CS algorithm contains a population of nests or eggs. Each egg in a nest represents a solution and a cuckoo egg represents a new solution. If the cuckoo egg is very similar to the host’s, then this cuckoo egg is less likely to be discovered; thus, the fitness should be related to the difference in solutions. The better new solution (cuckoo) is replaced with a solution which is not so good in the nest. In the simplest form, each nest has one egg. When generating new solutions x(t+1) for, say cuckoo i, a Lévy flight is performed:
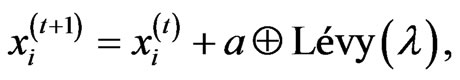 (7)
(7)
where a > 0 is the step size which should be related to the scales of the problem of interest. In most cases, we can use a = O (1). The product Å means entry-wise multiplications. Lévy flights essentially provide a random walk while their random steps are drawn from a Lévy distribution for large steps:
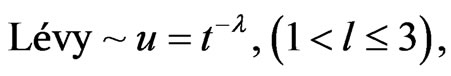 (8)
(8)
which has an infinite variance with an infinite mean. Here the consecutive jumps/steps of a cuckoo essentially form a random walk process which obeys a power-law step-length distribution with a heavy tail.
The rules for CS are described as follows:
• Each cuckoo lays one egg at a time, and dumps it in a randomly chosen nest;
• The best nests with high quality of eggs (solutions) will carry over to the next generations;
• The number of available host nests is fixed, and a host can discover a foreign egg with a probability pa Î [0, 1]. In this case, the host bird can either throw the egg away or abandon the nest so as to build a completely new nest in a new location.
The later assumption can be approximated by the fraction pa of the n nests which are replaced by new ones (with new random solutions). With these three rules, the basic steps of the CS can be summarized as the pseudocode shown bellow:
1) Define the objective function f(x), x = (x1, ..., xd)T.
2) Set n, pa and MaxGenerations parameters.
3) Generate initial population of n nests xi (i = 1, 2, ..., n).
4) Move a cuckoo (i) randomly by Lévy flights.
5) Evaluate the fitness Fi.
6) Randomly choose a nest (j) among n available nests.
7) If Fi > Fj then replace j by the new solution.
8) Abandon a fraction pa of worse nests and create the same fraction of new nests at new locations via Lévy flights.
9) Keep the best solutions (or nests with quality solutions).
10) Sort the solutions and find the best current solution.
11) If stopping criterion is not satisfied, increase generation number and go to step 4.
12) Postprocess results and find the best solution among all.
4. Experiments
CS has been applied to solve the ELD problems in two different test cases for investigating its optimization capability, where the objective function was limited within power ranges of the generating units and transmission losses are employed to demonstrate that were taken into account. Its performance was compared with six swarm optimization algorithm. We describe the test systems, the parameters’ settings and the experimental results as follows.
4.1. Test Systems
The CS and the other swarm algorithms were validated with two test systems consisting of three and six-generation units. The ELD problem was solved to obtain the minimum cost for the generation units with transmission losses. The Equation (6) was used as objective function for this problem.
4.1.1. Case 1: Three-Generating Unit System
This case study consists of three-generating units. The coefficients of fuel cost and the capacities of the generation units are shown in Table 1. In this case, the load demand expected (PD) to be determined is 150 MW.
However, the transmission loss coefficients matrix B is specified as:

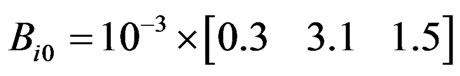
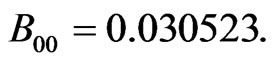
4.1.2. Case 2: Six-Generating Unit System
The six-generating unit system is presented here where the power system load demand (PD) is 700 MW and the fuel cost coefficients are given in Table 2. Comparing to Case 1, the complexity and non-linearity of the ELD problem are augmented.
The loss coefficients in the power transmission line (matrix B) are given by:
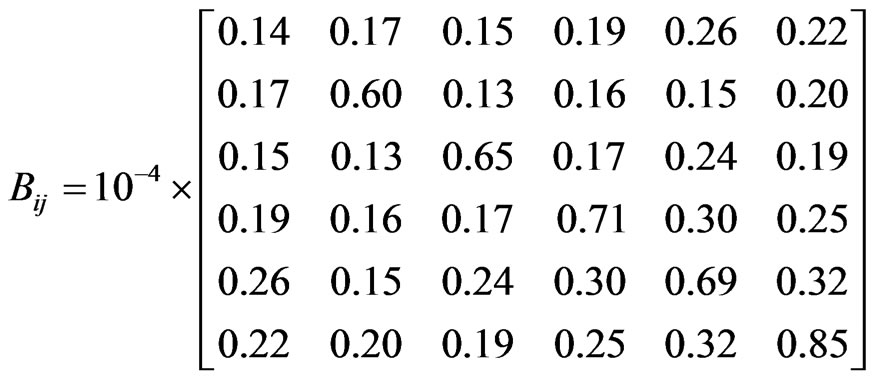
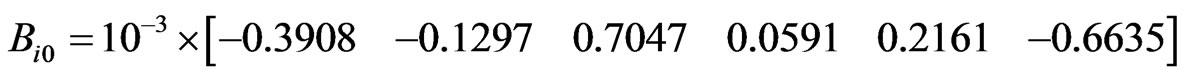
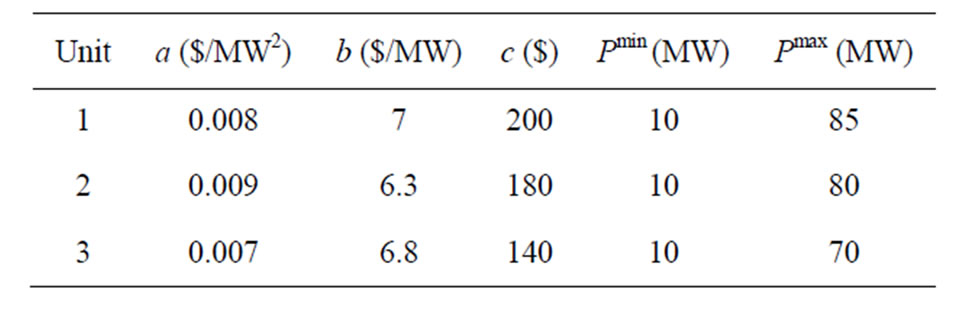
Table 1. Generator cost coefficients for the three-generating unit system.

Table 2. Generator cost coefficients for the six-generating unit system.

4.2. Algorithm’s Settings
We tested each test system for each swarm optimization algorithm. For every test, we carried on 20 independent runs with 5000 cycles per each run. We printed out worst, best and mean results as well the standard deviation within the set of 20 runs. Simulations were done on Intel Core i7 2630QM mobile processor with 4GB of RAM on Windows 7 × 64 Ultimate Operating System and Matlab R2010a. The parameters’ settings of each algorithm chosen by experimentation are cited bellow:
• Particle Swarm Optimization (PSO): P (particles) = 20, j1 (cognitive term) = 2, j2 (social term) = 2.
• Shuffled Frog Leaping Algorithm (SFLA): m (memeplexes) = 10, n (frogs) = 10, q (submemeplexes) = 2, Smax (step) = 5, iN (evolutions) = 5.
• Bacterial Foraging Optimization (BFO): S (bacteria) = 20, Nc = 10, Ns = 4, Nre = 4, Ned = cycles, ped = 0.25, dattract = 0.1, wattract = 0.2, hrepellant = 0.1, wrepellant = 10.
• Artificial Bee Colony (ABC): col (colony) = 20, BN
(employed bees) = 10, BC (onlookers) = 10, Cmax = 100.
• Harmony Search (HS): HMS (harmony memory size) = 2, HMCR (harmony memory considering rate) = 80, PAR (pitch adjusting rate) = 0.4.
• Firefly Algorithm (FA): n (fireflies) = 20, a (randomization factor) = 0.2, b0 (attractiveness) = 1.0, g (absorption coefficient) = 1.0.
• Cuckoo Search (CS): n (nests) = 20, pa (discovery rate) = 0.25.
4.3. Experimental Results
The results of CS algorithm were compared to those reported using PSO, SFLA, BFO and ABC [11]. HS and FA were implemented in this work for comparing with CS. The experimental results of overall simulations are shown in Table 3, where standard deviation and mean, worst and best costs for both test power systems were achieved.
In all cases, CS outperformed the solution founded by the others evaluated algorithms, in terms of reaching lowest worst cost, lowest mean cost solution and lowest standard deviation. As indicated in Table 3, CS presented the best convergence results and strong stability.
The optimal dispatch of the units is given in Table 4 for the three-generating unit system and in Table 5 for the six-generating unit system, in which CS results are compared to ABC and FA methods. The Tables 4 and 5 indicate the furnished power by each generating unit, the total generated power and the transmission losses for the best simulation.
It is clear from Tables 4 and 5 that the total power obtained by CS is closed to the constraint of the power demand. In this context, these CS approach performed better than the ABC and FA methods in terms of reducing the power transmission losses in the test case 2, while FA did not satisfy the power balance equality constraint (Equation (4)). Although the power outputs for PSO, SFLA, BFO and HS were not exhibited in these tables, all these methods achieved the active power balance.
5. Conclusions
In this work, Cuckoo Search is proposed for solving economic load dispatch problems. The effectiveness of this algorithm is demonstrated for test cases consisting of three and six-generating units. The results of the Cuckoo
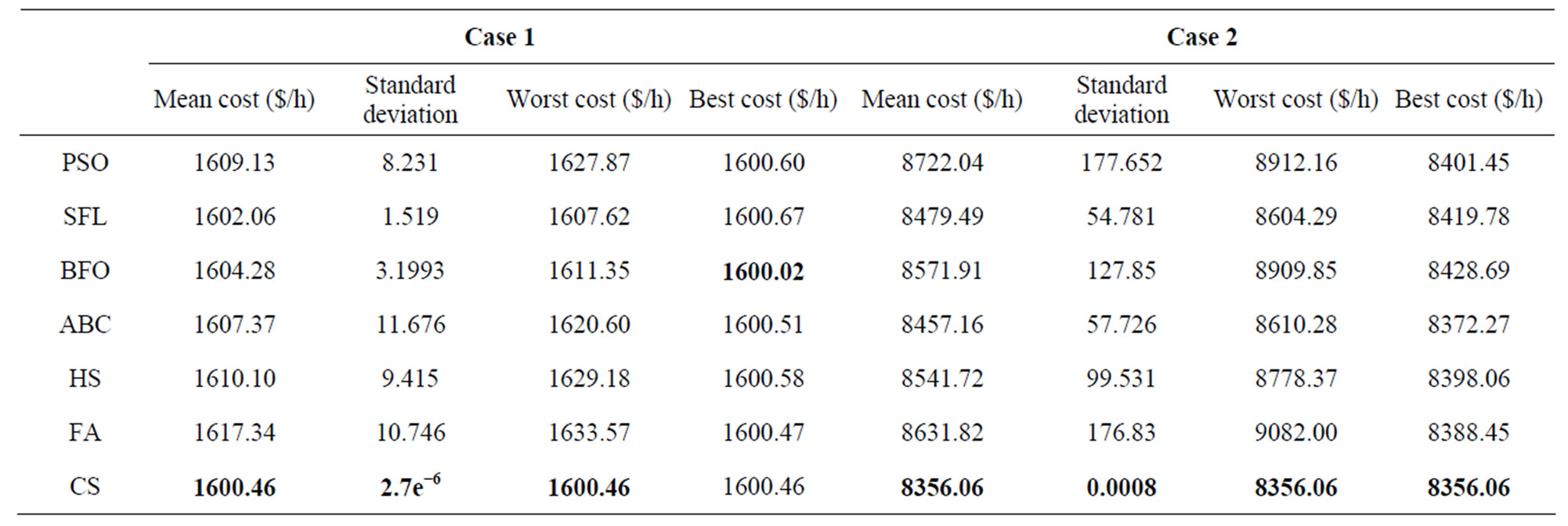
Table 3. Results for the seven swarm intelligence algorithms for minimizing the generation cost considering 20 runs.

Table 4. Results for the best simulations with three-generating units system.

Table 5. Results for the best simulations with six-generating units system.
Search are compared with that of other six swarm intelligence algorithms. Although in this work there are not methodological innovations, the comparison among the swarm methods is very interesting for potential real applications.
After contrasting the simulation results with the other algorithms, it is obviously seen that Cuckoo Search gives better results than other algorithms. Cuckoo Search is easy to implement and capable of finding feasible near global optimal solution.
In addition, the results substantiate the robustness, precise convergence and efficiency of this optimization algorithm. The main advantage of Cuckoo Search is a good ability for finding the solution. From the results obtained it can be concluded that Cuckoo Search is a competitive technique for solving complex nonsmooth optimization problems in power system operation.
6. Acknowledgements
The authors would like to thank Fundação de Amparo à Pesquisa do Estado de São Paulo for the financial support (Process FAPESP No 2011/08108-0).
REFERENCES
- L. Coelho and V. Mariani, “Combining of Chaotic Differential Evolution and Quadratic Programming for Economic Dispatch Optimization with Valve Point Effect,” IEEE Transaction on Power Systems, Vol. 21, No. 2, 2006, pp. 989-996. http://dx.doi.org/10.1109/TPWRS.2006.873410
- M. A. Abido, “A Novel Multiobjective Evolutionary Algorithm for Environmental/Economic Power Dispatch,” Electric Power Systems Research, Vol. 65, No. 1, 2003, pp. 71-81. http://dx.doi.org/10.1016/S0378-7796(02)00221-3
- Z. L. Gaing, “Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Constraints,” IEEE Transactions on Power Systems, Vol. 18, No. 3, 2003, pp. 1187-1197. http://dx.doi.org/10.1109/TPWRS.2003.814889
- J.-B. Park, K.-S. Lee, J.-R. Shin and K. Y. Lee, “A Particle Swarm Optimization for Economic Dispatch with Nonsmooth Cost Function,” IEEE Transactions on Power Systems, Vol. 20, No. 1, 2005, pp. 34-42. http://dx.doi.org/10.1109/TPWRS.2004.831275
- N. Sinha, R. Chakrabarti and P. K. Chattopadhyay, “Evolutionary Programming Techniques for Economic Load Dispatch,” IEEE Transactions on Evolutionary Computation, Vol. 7, No. 1, 2003, pp. 83-94. http://dx.doi.org/10.1109/TEVC.2002.806788
- B. K. Panigrahi, B. Ravikumar and V. Pandi, “Bacterial Foraging Optimisation: Nelder-Mead Hybrid Algorithm for Economic Load Dispatch,” IET Proceedings of Generation Transmission and Distribution, Vol. 2, 2008, pp. 556-565.
- S. Pothiya, I. Ngamroo and W. Kongprawechnon, “Ant Colony Optimization for Economic Dispatch Problem with Non-Smooth Cost Functions,” International Journal of Electrical power and Energy System, Vol. 32, 2010, pp. 478-487. http://dx.doi.org/10.1016/j.ijepes.2009.09.016
- V. Ravikumar Pandi, B. K. Panigrahi, M. K. Mallick, A. Abraham and S. Das, “Improved Harmony Search for Economic Power Dispatch,” Proceedings of the Ninth International Conference on Hybrid Intelligent Systems (HIS’09), Vol. 3, 2009, pp. 403-408.
- A. Bhattacharya and P. K. Chattopadhyay, “Biogeography-Based Optimization for Different Economic Load Dispatch Problems,” IEEE Transactions on Power Systems, Vol. 25, No. 2, 2010, pp. 1064-1077. http://dx.doi.org/10.1109/TPWRS.2009.2034525
- B. Shaw, S. Ghoshal, V. Mukherjee and S. P. Goshal, “Solution of Economic Load Dispatch Problems by a Novel Seeker Optimization Algorithm,” International Journal on Electrical Engineering and Informatics, Vol. 3, No. 1, 2011, pp. 26-42.
- A. B. S. Serapião, “Fundamentos de Otimização por Inteligência de Enxames: uma Visão Geral,” Revista SBA Controle & Automação, Vol. 20, No. 3, 2009, pp. 271-304.
- X. S. Yang and S. Deb, “Cuckoo Search via Lévy Flights,” Proceedings of World Congress on Nature and Biologically Inspired Computing, Coimbatore, 9-11 December 2009, pp. 210-214.
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of IEEE International Conference on Neural Networks, Perth, 27 November 1995, pp. 1942- 1948. http://dx.doi.org/10.1109/ICNN.1995.488968
- M. Eusuff and K. Lansey, “Optimizing of Water Distribution Network Design Using the Shuffled Frog-Leaping Algorithm,” Journal of Water Resources Planning and Manegement, Vol. 129, No. 3, 2003, pp. 210-225. http://dx.doi.org/10.1061/(ASCE)0733-9496(2003)129:3(210)
- K. M. Passino, “Biomimicry of Bacterial Foraging for Distributed Optimization and Control,” IEEE Control Systems Magazine, Vol. 22, No. 3, 2002, pp. 52-67. http://dx.doi.org/10.1109/MCS.2002.1004010
- D. Karaboga and B. Basturk, “A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm,” Journal of Global Optimization, Vol. 39, No. 3, 2007, pp. 459-471. http://dx.doi.org/10.1007/s10898-007-9149-x
- Z. W. Geem, J. H. Kim and G. V. Loganathan, “A New Heuristic Optimization Algorithm: Harmony Search,” Simulation, Vol. 76, No. 2, 2001, pp. 60-68. http://dx.doi.org/10.1177/003754970107600201
- X. S. Yang, “Firefly Algorithms for Multimodal Optimization”. In: O. Watanabe and T. Zeugmann, Eds., Stochastic Algorithms: Foundations and Applications. Lecture Notes in Computer Science, Springer-Verlag, Berlin, 2009, pp. 169-178.
- M. Tuba, M. Subotic and N. Stanarevic, “Modified Cuckoo Search Algorithm for Unconstrained Optimization Problems,” Proceeding of the European Computing Conference, Paris, 2011, pp. 263-268.

