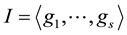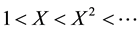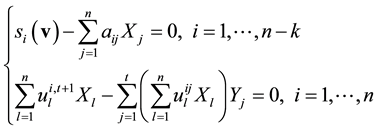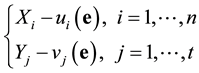Journal of Information Security
Vol.06 No.03(2015), Article ID:58256,8 pages
10.4236/jis.2015.63024
Grӧbner Bases Method for Biometric Traits Identification and Encryption
Mohamed Sayed*
Faculty of Computer Studies, Arab Open University, Kuwait City, Kuwait
Email: msayed@aou.edu.kw
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
Biometric identification systems are principally related to the information security as well as data protection and encryption. The paper proposes a method to integrate biometrics data encryption and authentication into error correction techniques. The normal methods of biometric templates matching are replaced by a more powerful and high quality identification approach based on Grӧbner bases computations. In the normal biometric systems, where the data are always noisy, an approximate matching is expected; however, our cryptographic method gives particularly exact matching.
Keywords:
Biometrics, Cryptography, Grӧbner Bases

1. Introduction
Digital data sent over communication channels are subject to distorting as a result of various circumstances such as electromagnetic fluctuations. Also, it might not be able to restore correct data from a hard disk or a digital audio (or video) system as most of the storage media is liable for errors. Another extreme example is the images remitted from space-probes, where a considerable error rate takes place and re-transmission is often not possible. The last example is the biometric feature vectors made of the attributes of the individuals which are noisy by nature. The consequence is that the digital data received (read or captured) may be not the same as the primarily sent (stored or enrolled). In this regard codes provide a methodical technique to transmit messages, with some supplementary information (check digits) in such a way that an error occurring in the original messages will not only be detected by the receiver, but in many cases, it could be corrected. More algebraic structures should be added to the code spaces to solve the decoding and encoding problems efficiently. In particular, linear codes are excessively exploited for controlling errors because they are well understood, powerful and easy to generate.
Biometrics can be defined as a largely automated measurement of physiological and behavioral characteristics that are used to prove or confirm identities of human beings [1] [2] . The physiological characteristics are the physical human traits such as hand shape, face, fingerprints, eyes, ear shapes, and hand veins. The behavioral characteristics of human beings are the way to sign their names, walk, speak or even keystroke dynamics; interested readers are referred to the literature [3] -[9] . Biometric identification methods show several particularities over traditional methods such as identification cards (tokens) and personal identification numbers (passwords) for many reasons. For example, users to be identified have to attend physically at the particular place of identification [10] . Also, biometric based identification systems avoid carrying tokens or remembering passwords. In addition, biometrics prevents misuse of stolen identification cards, credit cards and passports. Eventually, biometric systems can work in verification (authentication) or identification modes [11] . Several serious matters have to be con- sidered when designing a successful biometric system such as users must be first enrolled in the system as biometric templates which are securely stored in a database or on smart cards issued to the users. These templates can be used for matching when the users need to be identified or authorized to log into the secured system. This means that before the system can be used, during the enrollment step, the biometric imprints are acquired and data extracted from that imprints are saved as biometric templates in a central database. Later, during the authentication step, a new biometric imprint is acquired and the data extracted from that imprint are compared with the reference template [12] . The result of that comparison, with (a very small) percentage of error, is a match or no match.
Once a biometric trait is captured, residual random noise is removed by using filters (as a directed smoothing process); see for instance [13] . Then, the extracted feature vector or codeword, as we will more commonly call (see below), is turned out as a binary vector. Since the binary feature vectors of biometric templates acquired from the same person are most probably different from each other, it is necessary to detect and rectify the difference between the data acquired in the enrollment and verification steps [14] [15] . This correction takes the place of the normal templates matching in present biometric systems. Therefore, the matching between the enrolled and verified feature vectors can be modeled as transmitting messages through a noisy communication channel. Thus, the proposed matching algorithm measures diversities between the extracted and enrolled codewords. Each codeword (or bit string) is represented (or encoded) into secure data by computing its syndrome with respect to a preferable low-density parity-check (LDPC) code. The LDPC codes were first discovered by Gallager in 1962 [16] . In this work we develop a new biometric authentication algorithm that is not only based on the data contained in biometric templates but also on a randomly selected codeword from an LDPC code. Consequently, we propose a syndrome decoding algorithm (as replacement of matching process) based on Grӧbner bases calculations as a decoding scheme for the combination of data contained in biometric traits and suggested codewords.
A Grӧbner basis as a vigorous tool initiated from a commutative algebra is defined as a set of polynomials computed, using Buchberger’s algorithm [17] , from another set of polynomials. Grӧbner bases algorithms have been comprehensively studied, revised and implemented on most computer-algebra systems. In addition, Grӧbner bases have many interesting properties and applications in commutative (and non-commutative) algebra [18] - [20] . For instance, we can decide ideal membership or ideal equivalence with the aid of Grӧbner bases. Also, the elimination property of Grӧbner bases enables us to solve non-linear systems of algebraic equations in multiple variables. The application that we are actually interested in is to use Grӧbner bases in cryptography and, therefore, in biometric identification systems. In the case of binary linear codes, the Grӧbner bases will consist of all binomials which correspond to the problem’s codewords. The first connection between linear codes and Grӧbner bases was established in [21] . The main obstacle to our algorithm is that the computations of Grӧbner bases are expensive, and (in non-commutative algebras) are not guaranteed to stop [22] .
2. Theoretical Background
In this section, we give the substantial background required to understand the syndrome decoding problem and present some principles of linear codes. We also recall the elementary theory of Grӧbner basis algorithm for the case of multivariate polynomials. We show that the basic component of the Grӧbner basis theory is the concept of polynomial reduction that is used to compute the appropriately defined normal form of a specified polynomial.
2.1. Syndrome Decoding Problem
Let 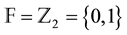 be the finite field of two elements and let n and k be positive integers with
be the finite field of two elements and let n and k be positive integers with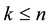 . In this work we assume that the feature vectors that represent biometric traits are given as elements of the vector space
. In this work we assume that the feature vectors that represent biometric traits are given as elements of the vector space . The (Hamming) weight of a word
. The (Hamming) weight of a word 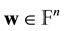 is defined to be the number of nonzero entries in
is defined to be the number of nonzero entries in 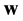 and the (Hamming) distance of
and the (Hamming) distance of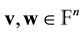 , denoted by
, denoted by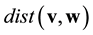 , is the weight of the difference
, is the weight of the difference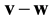 . A coding function
. A coding function 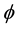 is defined by the injective mapping
is defined by the injective mapping
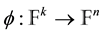 .
.
Let 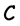 be an
be an  -code for some n and k. We say that
-code for some n and k. We say that
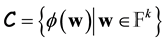
is a linear code of length n and dimension k over 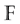 if it forms a subspace of
if it forms a subspace of . The rate of
. The rate of 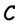 is
is 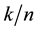
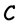
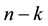
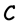

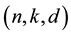
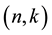
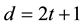
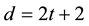
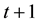
A generator matrix for the code 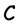
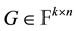
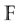
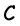
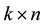
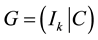
which produces the code 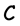
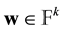
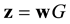
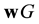
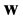
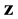
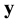
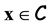
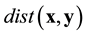
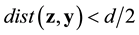
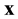
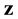
The parity-check binary matrix of such code 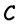
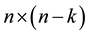
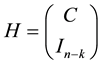
We define the syndrome 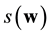
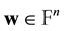
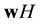
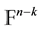
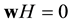
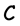
2.2. Grӧbner Bases
We introduce some basic definitions which we need to explain the Grӧbner basis theory. We only cite the theorem for the existence of the Grӧbner basis of an ideal. In 1965 Buchberger [17] gave an appropriate framework for the study of polynomial ideals in
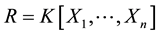
multivariate polynomials in commuting n variables over a computable field, with an introduction of Grӧbner basis. Furthermore, Mora [19] presented an algorithm for
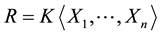
multivariate polynomials in non-commuting n variables over a computable field. We can say that both Buchberger and Mora algorithms, which based on a generalization of the Euclidean division algorithm to several variables, use the reality that coefficients are in a specified field. Therefore, given any two polynomials f and g, we can write f as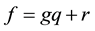
then, using the generalized division algorithm, we can write a polynomial f as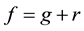
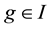
while, in several variables case, there are numerous preferences for the term ordering, see [18] . It is worth noting that the computation of Grӧbner basis could vary according to the type of ordering. A Grӧbner basis for an ideal has the property

Buchberger not only proved that each ideal has a basis for which the problem of ideal membership is computationally solvable, he also described an algorithm that can be exploited to get such a basis. Here, we should mention that polynomial reduction is the cornerstone in the Grӧbner bases algorithms as it represents the most intensive portion in terms of computations. In this regard we say that a polynomial f reduces to a different polynomial r, denoted as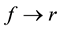
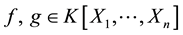
we define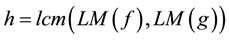
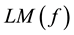
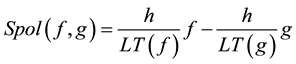
where 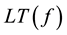
Of course, in non-commutative case the situation is more sophisticated since the monomials are words and there can be either more than one S-polynomial or none. A finite set of polynomials 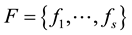
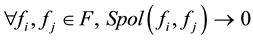
Now we are in a position to give the layout of the Buchberger algorithm. It launches with the initial basis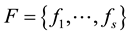
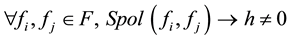
then h is appended to the basis. The process, with other added technical details, is reiterated till we obtain a basis satisfying the condition that is mentioned above. In the commutative situation, Buchberger showed that the process constantly terminates and gives at the end a Grӧbner basis. On the other hand, Mora noted that the process in non-commutative case does not always terminate―but, when it does, it should produce a Grӧbner basis.
For the proofs of the existence and uniqueness of a Grӧbner basis (in fact reduced Grӧbner basis) G for an ideal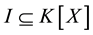
3. Syndrome Decoding and Grӧbner Bases
The interaction between coding theory and Grӧbner bases has been observed from the property that each function from 
Let 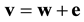
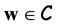
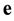
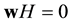
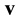
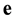
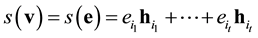
where 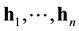
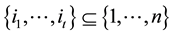
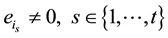
In order to solve the syndrome decoding problem we need to find such linear combination that gives the syndrome vector.
Let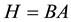
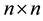
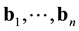

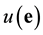
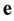
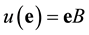
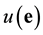

Then, we can recover the error vector as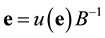
For any two vectors 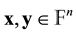
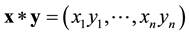
We can write the star product of two columns 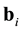
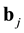
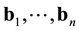
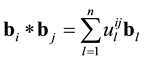
where 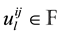
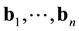
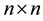
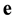
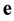
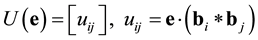
The relation between 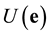
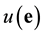
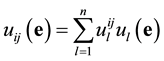
Now we can express the unknown syndromes in terms of the known syndromes as
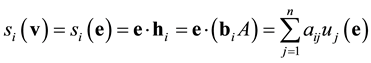
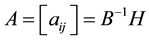
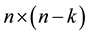
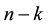

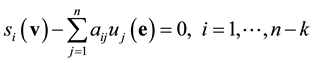
Since the rank of 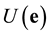
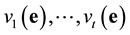
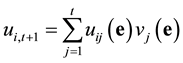
By representing 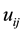
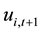

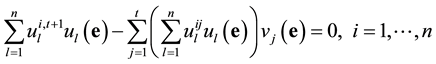
Let the unknowns 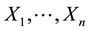

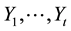
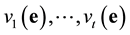
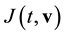
The ideal generated by the combined system defines the set of solutions that satisfies both systems. The reduced Grӧbner basis of the combined system with respect to a monomial ordering takes the form
where t is the smallest positive integer such that the system has solution (see the proof and some details on all of the above in Bulygin and Pellikaan [25] ). The unique solution of the system corresponds to the unknown syndrome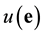
4. Biometric Matching Algorithm
In [26] [27] we showed that the biometric imprint (for security reason) is stored in encrypted binary form instead of plain-text. The biometric authentication device should agree access as long as two (enrolled and identified) biometric feature vectors do not differ by more than a definite amount of bits (the threshold). Here, the biometric identification systems should be able to deal with a large amount of bits. One more difficulty is how to design a system that can remedy 10% to 20% anticipated errors in extracted feature vectors [28] . Therefore, we require an 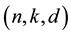
A biometric image is acquired and a feature vector is extracted from an enhance version of such image. Let 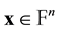
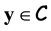
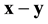
The authentication process is similar to the enrollment process for any new acquired biometric image. The result of such process is called the match score. Here, we assume that the number of errors is fewer than the code correcting capacity. Algorithm 2 shows how to verify (match)a feature vector of a new captured biometric trait.
Our technique is in fact different from conventional biometric authentication techniques which use numerical measure of the similarity of two biometric traits acquired at enrollment and verification steps. These conventional biometric systems require powerful digital signal processing algorithms in order to enhance the captured images before extracting the hidden characteristics. This process, which is called feature vector extraction, indeed plays the most critical part of biometrics identification. Our method is able to overcome most of the problems which might be resulting from the extraction of the biometric information as binary feature vectors from the realization of biometric traits.
5. Experimental Result
The implementation (as a proof-of-concept prototype) of our more promising approach has been done using various feature vectors of fingerprints and palm vein images as test data. We evaluated the algorithm using samples of 50 different users, with 5 samples per each user. The algorithm was implemented using an interpreted code as well as several built-in functions of MAGMA [29] . Because of our particular and special error correction and encryption approach the feature vectors exploited here are different from the biometric feature vectors used in the traditional biometric systems. For example, the dimension of the required code is minimal compared to other cryptographic based biometric systems. Using our approach, we can accept poor-quality biometric images which is always rejected (before matching) in most of conventional biometric technologies. Our approach also enables the use of low-cost sensors or even wireless biometric systems. For the used segmentation process and feature vectors extraction strategies the reader is referred to the literature [26] [27] . The LDPC code (with appropriate dimension), together with its standard generated matrix, was taken as the decoding strategy and proved to achieve optimal performance in terms of templates matching. We obtained an equal error rate of 0.1% for both false acceptance rate and false rejection rate, while the rate is about 5% with a template matcher in most conventional biometric systems.
Although the proposed approach does not yet fulfil the anticipated performance in terms of a Grӧbner basis computation complexity and latency, it does provide a low-cost secure biometric encryption architecture. On top of that it reveals various factors and provides beneficial insights that motivate the researchers in the area of integrating computational algebra with biometrics. The method is also suitable for other biometric systems such as iris biometrics that seem also very promising. All of these reasons make the algorithm feasible for different practical uses.
6. Conclusion
Even though many commercial and academic systems for biometrics identification are working out, the considerable number of publications on this domain states the necessity for extensive research for the sake of obtaining better performance and enhancing the reliability of such systems. In this paper, the problem for merging biometrics and cryptography was tackled. We used an algebraic method that allowed an exact recovery of a given a binary word (representing a biometric feature vector) using a randomly chosen word from a proposed code. We showed how to match a feature vector of a biometric trait by exploiting the theory of error-correcting codes over the field of two elements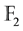
Cite this paper
MohamedSayed, (2015) Grobner Bases Method for Biometric Traits Identification and Encryption. Journal of Information Security,06,241-249. doi: 10.4236/jis.2015.63024
References
- 1. Raina, V.K. (2011) Integration of Biometric Authentication Procedure in Customer Oriented Payment System in Trusted Mobile Devices. International Journal of Information Technology Convergence and Services, 1, 15-25. http://dx.doi.org/10.5121/ijitcs.2011.1602
- 2. Vacca, J.R. (2007) Biometric Technologies and Verification Systems. Elsevier Science & Technology.
- 3. Sayed, M. and Jradi, F. (2014) Biometrics: Effectiveness and Applications within the Blended Learning Environment. Journal of Computer Engineering and Intelligent Systems (CEIS), 5, 1-8.
- 4. Rosdi, B.A., Shing, C.W. and Suandi, S.A. (2011) Finger Vein Recognition Using Local Line Binary Pattern. Sensors, 11, 11357-11371. http://dx.doi.org/10.3390/s111211357
- 5. Zhou, Y. and Kumar, A. (2011) Human Identification Using Palm-Vein Images. IEEE Transactions on Information Forensics and Security, 6, 1259-1274. http://dx.doi.org/10.1109/TIFS.2011.2158423
- 6. Xi, X., Yang, G., Yin, Y. and Meng, X. (2013) Finger Vein Recognition with Personalized Feature Selection. Sensors, 13, 11243-11259. http://dx.doi.org/10.3390/s130911243
- 7. Yang, J.F. and Yan, M.F. (2010) An Improved Method for Finger-Vein Image Enhancement. Proceedings of the 2010 IEEE 10th International Conference on Signal Processing, Beijing, 24-28 October 2010, 1706-1709. http://dx.doi.org/10.1109/icosp.2010.5656832
- 8. Teoh, A., Gho, A. and Ngo, D. (2006) Random Multispace Quantization as an Analytic Mechanism for Biohashing of Biometric and Random Identity Inputs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 28, 1892-1901. http://dx.doi.org/10.1109/TPAMI.2006.250
- 9. Tome, P., Vanoni, M. and Marcel, S. (2014) On the Vulnerability of Finger Vein Recognition to Spoofing. IEEE International Conference of the Biometrics Special Interest Group (BIOSIG), 230.
- 10. Raina, V.K. and Pandey, U.S. (2011) Biometric and ID Based User Authentication Mechanism Using Smart Cards for Multi-Server Environment. 5th National Conference on Computing for Nation Development, 5BVICAM, New Delhi, 10-11 March 2011.
- 11. Jain, A. and Aggarwal, S. (2012) Multimodal Biometric System: A Survey. International Journal of Applied Science and Advance Technology, 1, 58-63.
- 12. Yang, J. (2010) Biometric Verification Techniques Combing with Digital Signature for Multimodal Biometrics Payment Systems. IEEE 4th International Conference on Management of e-Commerce and e-Government, Chengdu, 23-24 October 2010, 405-410. http://dx.doi.org/10.1109/icmecg.2010.88
- 13. Yang, J.F. and Yang, J.L. (2009) Multi-Channel Gabor Filter Design for Finger-Vein Image Enhancement. Proceedings of the 5th International Conference on Image and Graphics, Xi’an, 20-23 September 2009, 87-91. http://dx.doi.org/10.1109/icig.2009.170
- 14. Sutcu, Y., Rane, S., Yedidia, J.S., Draper, S.C. and Vetro, A. (2008) Feature Transformation for a Slepian-Wolf Biometric System Based on Error Correcting Codes. Computer Vision and Pattern Recognition (CVPR) Biometrics Workshop, Anchorage, 1-6.
- 15. Kang, W. and Wu, Q. (2014) Contactless Palm Vein Recognition Using a Mutual Foreground-Based Local Binary Pattern. IEEE Transactions on Information Forensics and Security, 9, 1974-1985. http://dx.doi.org/10.1109/TIFS.2014.2361020
- 16. Gallager, R. (1962) Low-Density Parity-Check Codes. IEEE Transactions on Information Theory, 8, 21-29. http://dx.doi.org/10.1109/TIT.1962.1057683
- 17. Buchberger, B. (1985) Grobner Bases: An Algorithmic Method in Polynomial Ideal Theory. In: Bose, N.K., Ed., Multidimensional System Theory, D. Reidel, Dordrecht.
- 18. Becker, T., Kredel, H. and Weispfenning, V. (1993) Grobner Bases: A Computational Approach to Commutative Algebra. Springer-Verlag, London.
- 19. Borges-Trenard, M.A., Borges-Quintana, M.M. and Mora, T. (2000) Computing Grobner Bases by FGLM Techniques in a Non-Commutative Setting. Journal of Symbolic Computation, 30, 429-449. http://dx.doi.org/10.1006/jsco.1999.0415
- 20. Sayed, M. (2009) Coset Enumeration of Symmetrically Generated Groups Using Grobner Bases. International Journal of Algebra, 3, 693-705.
- 21. Cooper, A.B. (1992) Towards a New Method of Decoding Algebraic Codes Using Grobner Bases. 10th Army Conference on Applied Mathematics and Computing, 93, 293-297.
- 22. Arnold, E.A. (2003) Modular Algorithms for Computing Grobner Bases. Journal of Symbolic Computation, 35, 403-419. http://dx.doi.org/10.1016/S0747-7171(02)00140-2
- 23. Sayed, M. (2011) Coset Decomposition Method for Decoding Linear Codes. International Journal of Algebra, 5, 1395-1404.
- 24. Heegard, C., Little, J. and Saints, K. (1995) Systematic Encoding via Grobner Bases for a Class of Algebraic-Geometric Goppa Codes. IEEE Transactions on Information Theory, 41, 1752-1761. http://dx.doi.org/10.1109/18.476247
- 25. Bulygin, S. and Pellikaan, R. (2009) Bounded Distance Decoding of Linear Error-Correcting Codes with Grobner Bases. Journal of Symbolic Computation, 44, 1626-1643. http://dx.doi.org/10.1016/j.jsc.2007.12.003
- 26. Sayed, M. (2015) Coset Decomposition Method for Storing and Decoding Fingerprint Data. Journal of Advanced Computer Science & Technology, 4, 6-11. http://dx.doi.org/10.14419/jacst.v4i1.3958
- 27. Sayed, M. (2015) Palm Vein Authentication Based on the Coset Decomposition Method. Journal of Information Security, 6, 197-205. http://dx.doi.org/10.4236/jis.2015.63020
- 28. Yang, G.P., Xi, X.M. and Yin, Y.L. (2012) Finger Vein Recognition Based on a Personalized Best Bit Map. Sensors, 12, 1738-1757. http://dx.doi.org/10.3390/s120201738
- 29. Bosma, W., Cannon, J.J., Fieker, C. and Steel, A., Eds. (2010) Handbook of Magma Functions, Edition 2.16.
NOTES
*On leave from Faculty of Engineering, Alexandria University, Egypt.