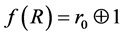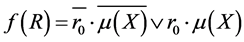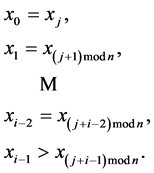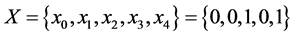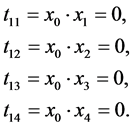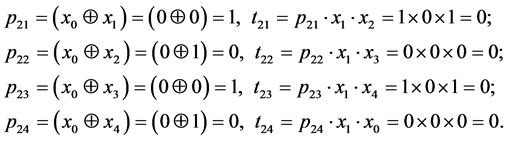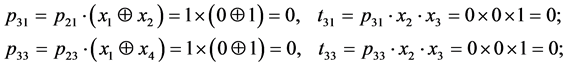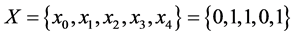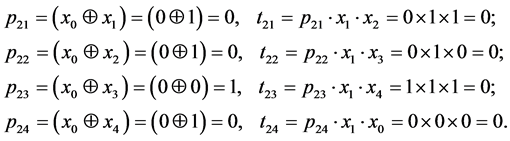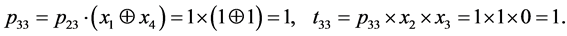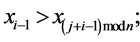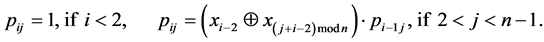Journal of Information Security
Vol.05 No.04(2014), Article ID:50983,9 pages
10.4236/jis.2014.54020
Method of Designing Generators of Pseudorandom Sequences for Information Protection Based on Shift Register with Non-Linear Feedback Function
Saleh Al-Omar
Department of Engineering, Al-Ahliyya Amman University, Amman, Jordan
Email: salehalomar@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 July 2014; revised 25 August 2014; accepted 20 September 2014
ABSTRACT
This paper proposes an efficient, high-tech method of construction of pseudorandom binary sequences generators with a repetition period 2n for n-bit shift register with a nonlinear feedback function. The developed method is illustrated by constructing a nonlinear function feedback shift register. It is proved that the offered method requires the realization of a memory size proportional to n2 that allows making successful use of suitable generators for practical use on the shift register of the longer word.
Keywords:
Pseudorandom Sequences, Non-Linear Feedback Function, Information Protection

1. Introduction
In tasks of information protection, statistical monitoring and diagnosis, modeling and designing, generators of pseudorandom sequences are widely used. The effectiveness of these generators in informational technologies is defined by specific features of using them [1] .
Pseudorandom objects are very important in modern systems of information protection [2] . Especially important role in this dynamically developing domain is played by pseudorandom binary sequences, which are used as a baseline for one of three types of information security algorithms—flow algorithms [3] . Pseudorandom sequences are widely used for generation of keys for the symmetrical data protection algorithms and pseudorandom binary strings for protocols of authentication of remote users in integrated systems [4] . In modern conditions of productivity growth of computational systems and possibilities to unite a huge number of computers in a network for solving problems of security breach, the problem of adequate increasing the reliability of information security becomes more actual, including methods of improving means of obtaining and using pseudorandom sequences.
Protective features of pseudorandom sequences and functional transformations in theoretical plan are defined by the principal impossibility of analytical solutions of the systems of non-linear Boolean equations [5] . This feature of Boolean transformations lies in the heart of using binary sequences and Boolean functions in information security systems. That is why the level of protection of data with using pseudorandom sequences is directly dependent on the nonlinearity of Boolean functions, which are used to generate pseudorandom sequences. From this, important reserve for increasing effectiveness of means of information protection, which use pseudorandom sequences, is in improving means of formation such sequences in the direction of increasing the nonlinearity of Boolean transformations, which they use.
Thus, at the current stage of development of information protection, the problem of developing methods and approaches for increasing effectiveness of hardware-software means of generation of pseudorandom binary sequences is actual.
2. Analysis of the Current State of the Problem of Effective Generation of Pseudorandom Sequences for Information Security Problems
2.1. Modern Generators of Pseudorandom Sequences Oriented to Be Used in Systems of Information Protection Are Built on the General Principles [5]
· Divergence—the notion which came from the theory of dynamical systems and consisted in the fact that algorithm of a generator should provide diverging sequence of binary n-bit words, that is the sequence, the repetitive cycle of which tends to 2n [5] .
· Nonlinearity of used functions of transformations, which provides complexity of recognition of generation functions of pseudorandom sequences.
· Computing complexity which means computational incompressibility of the procedures for pseudorandom sequences generation.
Mentioned principles, formulated on the theoretical level, are not strictly defined and partly overlap each other [6] . The notion of divergence is often used if the base for the functional transformation, which lies in the base of the generator, is a special case of the theory of numbers [6] . For bit transformations the problem of divergence which means to provide the repetitive cycle of 2n − 1, theoretically can be solved only for linear feedback functions: they must be isomorphic irreducible polynomials in Galois fields. For nonlinear functions of the bit transformation, divergence problem has a solution only for special cases [7] .
2.2. A Criteria of Quality of the Generators of Pseudorandom Sequences Oriented to Be Used in Systems of Information Protection the Following Indicators Are Mostly Used [8]
· Statistical criteria which allows to estimate the probability characteristics of the generated sequence [6] ;
· Divergence criteria of generator work—is estimated by the minimal length of cycle appeared during the run;
· Unpredictability of the generator—is estimated by the complexity of the special algorithm-recognizer which allows to distinguish the generated sequence from random [7] ;
· Rate of sequence generation.
Really important when these criteria are considered is the principle, formulated in [8] and postulating that the criterion for determining the randomness is always determined by the class of the problems in which this randomness will be used, that is: use should determine the target probability distribution with the specified degree of approximation and the importance of each of the above criteria.
The third of mentioned earlier criteria of quality of pseudorandom sequences generators is their algorithmic unpredictability, which stipulates the complexity of the algorithm which can predict next values by using data from previous samples [9] . From the point of reliability of data protection it is the third criterion is a determining, because all breaches in security provided by using pseudorandom sequences are reduced to the extrapolation of the recent [9] . It is proved that irreversible transformations should be used to make the sequence meet the unpredictability demand. For flow algorithms widely used in data transfers across networks and telecommunication systems, high speed of generation of the sequence is very important [3] . Exclusion of the possibility of gaining access to programs which implement the generation process is also very important. Based on the last two demands, more preferable is a variant of hardware realization of the generators. In this case, significant criterion of quality of means of pseudorandom sequences generation is their complexity. In practice, the most important class of generators of pseudorandom sequences is the generators based on shift registers with linear feedback—LFSR (Linear Feedback Shift Register). The main advantage of such generators is the fact that due to the developed method of synthesis of the feedback functions their acyclic work is provided (it means the cycle is 2n − 1 with n-bit shift register) along with the simplicity of circuit implementation on a hardware level and high performance [8] . So far as the maximum number of different combinations of n binary digits is 2n, period of the generated sequence cannot exceed 2n. If LFSR gets into a state with zero values of all bits, it cannot go to another state. That is why zero state shouldn’t appear if the initial state nonzero. Therefore, the maximum number of possible states is 2n ‒ 1. Maximal length sequence will be provided in case when the feedback function is a simple polynomial in Galois fields [4] . Thus the number G(n) of simple polynomials in Galois fields, and therefore the quantity of sequences with length of 2n ‒ 1 formulated by LSFR is determined by the formula:
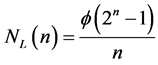 (1)
(1)
where f(2n ‒ 1)—Euler number—quantity of integer, including ones, which are less than 2n ‒ 1 and those, which don’t have common divisors with 2n ‒ 1.
Theoretically the maximum possible number of states of n-bit shift register equals 2n. Respectively, maximum repetition period of the binary sequence formulated by a nonlinear shift register of such length is 2n too. Such sequences are called Bruijn sequences. Number N(n) of nonlinear feedback functions of n-bit shift register which provide the maximum repetition period is determined by the formula:
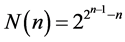 (2)
(2)
For example, for the 6-bit shift register (n = 6) according to (1) exist only 6 simple polynomials in Galois fields and respectively 6 linear functions which provide period of 26 ‒ 1 = 63 which is close to the maximum, though that number of nonlinear feedback functions for the register with the same bit number which provide the maximum period—26 according to (2) is 226 = 67108864.
Despite such a big number of nonlinear feedback functions, providing the maximum period of repetition of the sequence, finding them is a challenge, which hasn’t acceptable solution to date [4] . So, for n = 6 assuming that the total number of functions is 264, the maximum period is provided, on average, only by one of 264-26 = 240 functions.
3. Method of Finding Nonlinear Feedback Functions
The state of a shift register is characterized by w code which corresponds to the binary vector of Xw values of register bits:
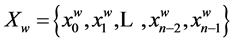
During the register shift new value of v code is determined by the following method:
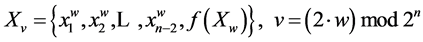
Suppose f(x1, x2,…, xn)—Boolean feedback function of n-bit shift register for which the following condition is true:
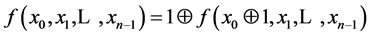 (3)
(3)
If the feedback function 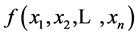 satisfies the condition (3), then each v code in the register is preceded by only one w code.
satisfies the condition (3), then each v code in the register is preceded by only one w code.
A set of codes which sequentially formulated in shift register with feedback feature which satisfies the condition [4] we will name the ring. Each of 2n possible codes in n-bit register is included into one of the rings.
Suppose we have two rings—A and B. If code w is included in A and the symmetrical to it code 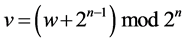 is included in B, then inverting the value of the function in these codes will lead to unite of A and B rings.
is included in B, then inverting the value of the function in these codes will lead to unite of A and B rings.
Proof: Binary vector 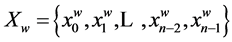 of state of the register corresponds to w code. Code e follows after w in the A ring:
of state of the register corresponds to w code. Code e follows after w in the A ring: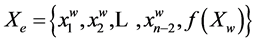 . When inverting the value of the feedback function
. When inverting the value of the feedback function
on code w, the following after w will be code u: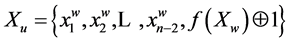 . Code v is symmetrical to w:
. Code v is symmetrical to w:
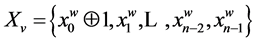 . According to (3.1)
. According to (3.1)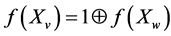 , that is why code u follows after v in the B ring. When inverting functions on code v, the following code will be e:
, that is why code u follows after v in the B ring. When inverting functions on code v, the following code will be e: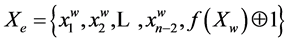 .
.
Therefore, when inverting functions on symmetrical codes which are included into different rings A and B, after w code there will be transition to code u 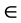 В. Later, serial pass of all codes of the ring B is performed, last of which is code v. From this code transition to code e
В. Later, serial pass of all codes of the ring B is performed, last of which is code v. From this code transition to code e 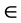 А is performed. Further all codes of the ring A are passed serially. Thus, rings A and B are combined into one ring.
А is performed. Further all codes of the ring A are passed serially. Thus, rings A and B are combined into one ring.
Offered method of synthesis of the nonlinear feedback function which provides full period is based on basic procedure of combining rings, obtained during cyclic shift.
The function of cyclic shift of the shift register equals to senior bit of the current code K.
 (4)
(4)
Obviously, that function (4) satisfies the condition (3). Function (4) forms NR rings, each of which includes codes with equal number of ones. Let’s denote with R(k) the ring, which includes code k. Suppose L(A)—num- ber of ones in codes of the cyclic ring A. For example, when n = 4 and k = 6: R(k) = {6(0110), 12(1100), 9(1001), 3(0011)}, L(R(k)) = 2.
Each of rings has only one minimal code. It is obvious that for any cyclic ring A ≠ R(0), minimal code q = min(A) is an odd number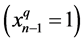
4. The Basic Procedure for Combining Cyclic Rings Is in Performing the Following Sequence
1. Initial value of the current code j is chosen randomly, 0 < j < 2n. Counter of h codes, for which the value of the feedback function is determined, is set to one: h = 1.
2. u = (2∙j) mod 2n + 1 is calculated. If calculated code u is minimal in its ring, which means u = min(R(u)), then the value of the feedback function on code j is determined as an inversion of the cyclic shift:
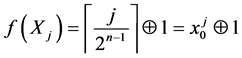
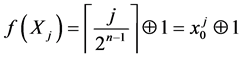
is greater than x.
3. The new value of the current code j: = (2∙j) mod 2n + f(Xj) is calculated. Increment of the counter is performed: h: = h + 1. If h ≤ 2n, then return to item 2, otherwise-end.
The function of cyclic transfer forms NR rings. Described procedure provides a connection of all these rings into one.
Proof: Combining of the rings is performed in pairs. Let’s consider random ring B, which consist of codes which include m ones (0 < m < n), minimum of them is denoted as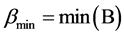
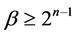
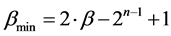
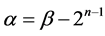
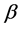
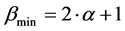
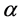
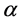
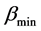
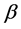
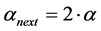
Transfer to the minimal code of the B ring possible from one code of the ring A: L(B) = L(A) + 1 except the situation when L(B) = 0. In this case one code is a predecessor of minimal codes for both rings. For example, when n = 4 code 1(0001) precedes the minimal code 0 of the ring {0} and the minimal code 1(0001) of the ring {1, 2, 4, 8}.
The minimal code of each of the rings (except the ring, which consist of zero code) is preceded by the code with less number of ones from other ring. It means that described procedure provides a binding of all rings, made by cyclic shift.
When k = 1 according to (4) RN(5,1) = 1 and, respectively, exist only one partial ring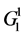
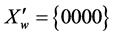
When k = 2 there are two partial rings: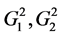
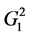
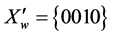
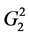
and, respectively, 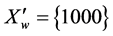
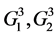
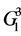
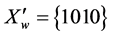
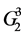
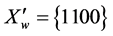
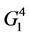
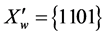
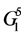
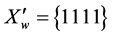
The resulting table of the values of the Boolean function 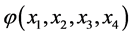
In algebraic normal form the synthesized function 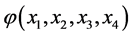
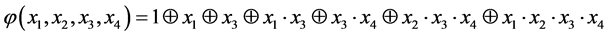
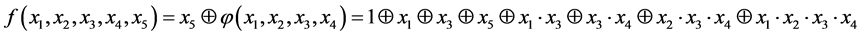
Let’s demonstrate that the proposed method of synthesis of the feedback function is constructive. An operation of setting value of the function 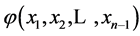
the ring which includes code 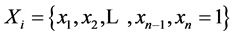
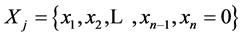
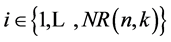
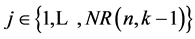
suggests a choice of one X code from all rings then it means that each ring is connected with one of the rings, codes of which have less number of ones. Thus all rings are connected into one that provides the maximum period of 2n repeats of the code in the shift register.
Described procedure for constructing the nonlinear feedback function opens opportunities for optimizations of parameters of generated pseudorandom binary sequences by choosing the ring from set of G. Since the procedure is consistent and includes element of choice, then choice can be done from selected criteria, for example, criterion of the maximum of nonlinearity or compliance to avalanche effect.
For comparative analysis of the effectiveness of the proposed method it is important to estimate the number of nonlinear feedback functions, which can be obtained from its use. The number NF(n) of Boolean functions which allow to synthesize the proposed method is determined by number of variants of choice of codes from partial rings. Since this choice is independent for each partial ring, then numeric value NF(n) is determined as a product of a number of variants for choice. With fixed number of k ones in the code of the ring, which contains n codes, number of variants to choose the code from partial ring is k. The total number of such rings is NF(n), numeric value of which is determined by the formula (2.12). Therefore, the total number of variants for choice of the code which contains k ones from the rings with length n is kNR(n,k). For rings with less length the number of variants of choice of the code is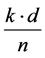
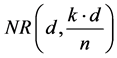
Table 1. Values of
NF(n) feedback functions which allows to synthesize the proposed method is defined by the following expression:
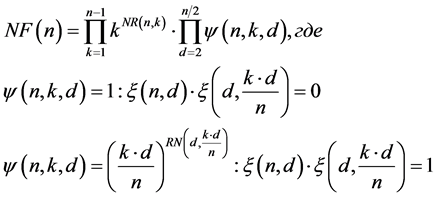
Analysis shows that developed method allows synthesizing 10 times more functions comparing with knows methods.
For n = 5 the proposed method allows to obtain NF(5) = 144 feedback functions, when the existent methods propose not more than 15 functions [8] . At the same time the proposed method is quite simple and technological [4] that provides higher performance compared to known methods. The proposed method is realized in software and successfully passed all tests.
The disadvantage of the method of building LFSR based on described procedure of combining elements of closed code groups is the fact, that time and amount of memory proportional to 2n is required for its implementation. A modification is proposed to significantly decrease computational complexity by narrowing the class of synthesized feedback functions and optimization of the procedure of building the function in disjunctive normal form.
Suppose the current vector of the values of bits of n-bit shift register is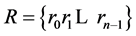
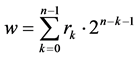
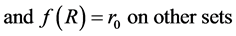
Feedback function will formed as:
where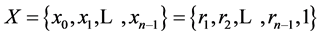
m(X) can be formed as disjunction of all tij terms:
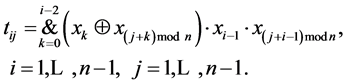
Set cannot be minimal if it contains at least one sequence of bits 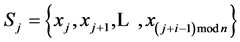
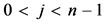
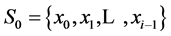
In particular, the set isn’t minimal if i ‒ 1 of corresponding senior bits of this sequence are equal and the junior bit of the sequence S0 is greater than junior bit of the sequence Sj:
In each term tij check of satisfying this condition is performed. If 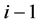
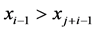
Condition is checked for all length of sequences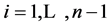
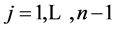
To extend the procedure of formation of the feedback functions, which provide full period, the previously described method of pre-unification of the two rings can be used. Let’s consider examples of work of the f1(X) function for n = 5 with different values of bits vector X.
Example 1.
Let’s determine terms for sequences with the length of one. The sequence of senior bits is S0 = {x0} = {0}. Next, let’s compare X0 with each bit x1, x2, x3, x4:
Note that for all sets with zero senior bit, values of t1j will always be zero.
Let’s determine terms for sequences with length i = 2 : S0 = {0, 0}.
It is obvious that all t2j have zero value. As long as values of the following tij depend on p2j, we will determine terms only for those values j, where p2j has value of one, thus j = 1 and j = 3. The length of the sequence i = 3, S0 = {0, 0, 1}. Let’s find terms for j = 1 and j = 3.
Zero values of p31 and p33 during calculations of the following terms convert the result into zero. Therefore, all tij for this set are equal to 0. f1(X), formed as disjunction of all tij terms, also obtains zero value. It means that code
Table 2. Terms tij for n = 5.
w, corresponding to Х = {0, 0, 1, 0, 1} set, has the minimal value in the ring. Really, w = 16 ´ 0 + 8 ´ 0 + 4 ´ 1 + 2 ´ 0 + 1 ´ 1 = 5 and the ring, where it is included, is {5, 10, 20, 9, 18}. We can see that 5 is the minimal value.
Example 2.
2.1 Since x0 = 0, then terms t11 = t12 = t13 = t14 = 0.
2.2 Let’s determine term for sequences with length of i = 2: S0 = {0, 1}.
All terms for t2j have zero values. Among values of p2j there is only one value p23 = 1, which can be used for further calculations. The rest of these values turn terms, to which they are included, into zero. Let’s consider the sequence of length i = 3. The sequence of three senior S0 = {0, 0, 1}. For all j values except j = 3, terms t3j will be zero. Determining p33 and t33:
If we have at least one term with value of 1, the value of the function f1(X) will also be one.
Therefore, for X = {0, 1, 1, 0, 1}, f1(X) = 1, it means code w = 13 isn’t a minimum in its ring. Let’s make sure that it is true. We obtain a ring by cyclic shift: {13, 26, 21, 11, 22}. Here we can see that the minimal value in this ring is 11, not 13. Table 3 shows the result of construction of the feedback function for a 5-bit shift register with minimal repetitive cycle.
Complexity of the developed algorithm of construction of the feedback function in Zhegalkin’s algebra is equivalent to the function itself.
Let’s estimate the complexity of the f1(X) function. To calculate one term tij the following number operations are required:
· i − 1 operations NXOR 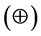
· 1 operation AND to check the condition
· i − 1 operations AND to unite all conditions.
So, in total we have 2i − 1 operations. The total complexity of calculation the terms for all values i and j is:
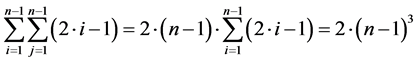
Another (n − 2)2 operations OR are required to unite all terms, that is to calculate the function m(X) 2(n − 1)3 + (n − 2)2 operations are required, therefore, the complexity is proportional to n3.
As we can see, the function is redundant. In each term tij calculations, which are made for ti‒1j, are performed. During paired comparison of the elements of the sequences S0 and Sj with length of i > 2 the results of the first i − 2 elements are known form the previous step. That is why the formula to determine tij can be written as:
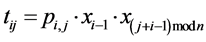
where pi,j-term, which compares for equality senior i − 1 bits of the sequences.
pij can be determined as:
Since for calculations of each tij constant number of operations is performed (1 operation when i = 1 and 4 otherwise), the complexity of the function m(Х) will be proportional to n2: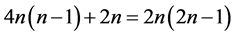
The amount of memory required to perform the algorithm is determined by necessity to save all terms tij, 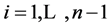
5. Conclusions
An approach is proposed for the construction of the important element of the contemporary systems for the pro-
Table 3. Construction of the feedback function.
tection of information-generators of pseudorandom binary sequences with the repetition period 2n on the basis of n-bit shift register with the nonlinear feedback function. Such generators are considerably simpler and more efficient compared with the generators constructed in the form of LFSR system and nonlinear inverter.
Within the common approach, based on the technology of the association “rings”, realization of which requires memory with size 2n, is developed with high-tech modification, which makes it possible to build the generators of pseudorandom sequences on the basis of the shift register with the nonlinear feedback function of with the use of memory, proportional to n2. The use of the method proposed makes it possible to build a suitable for the practical use in the telecommunication technologies. An experimental study made it possible with the use of the method proposed to build generators of word length up to 128 bit.
References
- Obeidat, A. (2012) Burst Error Correction Method Based on Arithmetic Weighted Checksums. Engineering, 4, 768- 773. http://dx.doi.org/10.4236/eng.2012.411098
- Luby, M. (1996) Pseudorandomness and Cryptographic Applications. Princeton University Press, Princeton, 273 p.
- Golomb, S.W. (1982) Shift Register Sequences. Aegean Park Press, Laguna Hill, 324 p.
- Menezer, A.J., Van Oorschot, P.C. and Vanstone, S.A. (1997) Handbook of Applied Cryptography. CRC Press, Boca Raton, 780 р.
- Sarkar, P. and Maitra, S. (2001) Efficient Implementation of “Large” Stream Cipher Systems. Proceeding of 3th International Workshop “Cryptographic Hardware and Embedded Systems” (CHES-2001), Springer-Verlag, 319-332.
- Key, E.L. (1976) An Analysis of the Structures and Complexity of Nonlinear Binary Sequence Generators. IEEE Transaction on Information Theory, 22, 732-736. http://dx.doi.org/10.1109/TIT.1976.1055626
- Sidorenko, V., Richter, G. and Bossert, M. (2011) Linearized Shift-Register Synthesis. IEEE Transaction on Information Theory, 57, 6025-6032.
- (2000) NIST Special Publicaion 800-22: A Statistical Test Suite for Random and Pseudorandom Number. 348 p.
- Gutierrez, J., Shparlinski, I.A. and Winterhof, A. (2003) On the Linear and Nonlinear Complexity Profile on Nonlinear Pseudorandom Number Generators. IEEE Transaction on Information Theory, 49, 60-64.