Materials Sciences and Applications
Vol.05 No.14(2014), Article ID:52196,7 pages
10.4236/msa.2014.514107
Binary Relations between Magnitudes of Different Dimensions Used in Material Science Optimization Problems Pseudo-State Equation of Soft Magnetic Composites
Krzysztof Z. Sokalski1*, Bartosz Jankowski2, Barbara Ślusarek2
1Institute of Computer Sciences, Częstochowa University of Technology, Częstochowa, Poland
2Tele and Radio Research Institute, Warszawa, Poland
Email: *sokalski_krzysztof@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 September 2014; revised 12 October 2014; accepted 10 November 2014
ABSTRACT
New algorithm for optimizing technological parameters of soft magnetic composites has been derived on the base of topological structure of the power loss characteristics. In optimization magnitudes obeying scaling, it happens that one has to consider binary relations between the magnitudes having different dimensions. From mathematical point of view, in general case such a procedure is not permissible. However, in a case of the system obeying the scaling law it is so. It has been shown that in such systems, the binary relations of magnitudes of different dimensions is correct and has mathematical meaning which is important for practical use of scaling in optimization processes. The derived structure of the set of all power loss characteristics in soft magnetic composite enables us to derive a formal pseudo-state equation of Soft Magnetic Composites. This equation constitutes a relation of the hardening temperature, the compaction pressure and a parameter characterizing the power loss characteristic. Finally, the pseudo-state equation improves the algorithm for designing the best values of technological parameters.
Keywords:
Soft Magnetic Composites, Scaling, Binary Relations, Pseudo-State Equation

1. Introduction
Recently novel concept of technological parameters’ optimization has been applied in Soft Magnetic Composites (SMC) by Ślusarek et al., [1] . This concept is based on assumption that SMC is a self-similar system where function of loss of power obeys the scaling law [2] -[4] . The efficiency of scaling in solving problems concerning power losses in soft magnetic composites has already been confirmed in [1] .
The scaling is very useful tool due to the three reasons:
• it reduces number of independent variables  and
and  to the effective one
to the effective one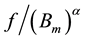 ,
,
• and determines general form of loss of power characteristic in a form of homogenous function in general sense (h.f.g.s.),
• as well as enables us to use binary relations between magnitudes of different dimensions.
Reduction of independent variables is based on definition of the h.f.g.s., namely, 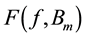 is the h.f.g.s. if:
is the h.f.g.s. if:
 (1)
(1)
According to the assumption concerning 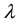 we are free to substitute any positive real number, for instance
we are free to substitute any positive real number, for instance
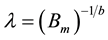 then we get:
then we get:
 (2)
(2)
where 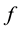 and
and 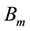 are frequency and pik of magnetic inductance, respectively.
are frequency and pik of magnetic inductance, respectively. 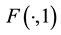 is an arbitrary function,
is an arbitrary function,
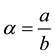 ,
,  are scaling exponents.
are scaling exponents.
Choice for the  depends on the power loss characteristics of investigated materials. In [1] we have modified the Bertotti decomposition rule [5] [6] which led to the following form for
depends on the power loss characteristics of investigated materials. In [1] we have modified the Bertotti decomposition rule [5] [6] which led to the following form for :
:
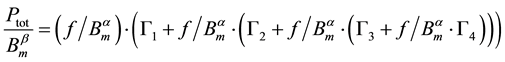 (3)
(3)
where





Figure 1. Selection of the power loss characteristics Ptot/(Bm)α vs. f/(Bm)α calculated according to (3) and Table 1 for Somaloy 500 [1] , T = 500˚C.
Figure 2. Selection of the power loss characteristics Ptot/(Bm)α vs. f/(Bm)α calculated according to (3) and Table 1 for Somaloy 500 [1] .
Table 1. Somaloy 500. Values of scaling exponents and coefficients of (3) vs. compaction pressure and hardening temperature, a selection from [1] .
power loss characteristics presented in Figure 1 and Figure 2 are different dimensions. So, we have to answer the following question: are we able to relate them in the optimization process which has been described in [1] ?
In this paper we will prove that if the considered characteristics obey the scaling, then the binary relation between them is invariant with respect to this transformation and comparison of two magnitudes of different dimensions has mathematical meaning. Reach measurement data of power losses in Somaloy 500 have been transformed into parameters of (3) vs. hardening temperature and compaction pressure Table 1 in [1] . Information contained in this table enable us to infer about topological structure of set of the power loss characteristics and finally to construct pseudo-state equation for SMC, and derive new algorithm for the best values of technological parameters.
2. Scaling of Binary Relations
Let the power loss characteristic has the form determined by the scaling (2). It is important to remain that 





Let us concentrate our attention at the point on the 

Let us take into account the two characteristics and let us assume that

Therefore, the considered binary relation is the strong inequality and corresponds to natural order presented in Figure 1 and Figure 2. The most important question of this research is whether (6) is invariant with respect to scaling:

Let 
• Let us perform the scaling with respect to 

where 
• Substituting appropriate relations of (8) to (7) we derive:

• Collecting all powers of 

Therefore (6) is invariant with respect to scaling. This binary relation has mathematical meaning and constitutes the total order in the set of characteristics.
3. Binary Equivalence Relation
The result derived in Section 2 can be supplemented with the following binary equivalence relation. Let

be the 





Theorem: 

4. Pseudo-State Equation of SMC
Let 
in 

state equation we transform each power loss characteristic into a number 


This function must satisfy the following condition. Let us concentrate our attention at the two following points:

Let us consider the two characteristics 





While, the other technological parameters powder compositions and volume fraction are constant. Let us assume that for (14) the following relation holds:

It results from the derived structure of 









Moreover, 


where the integration domain is common for the all characteristics. We have selected the common domain of Figure 1 and Figure 2:



where





Figure 3. Pseudo-Isotherm T = 500˚C of the Low-losses phase, according to data of Table 2 for Somaloy 500 [1] .
Table 2. V measure vs. hardening temperature and compaction pressure.

where 
In order to extent (19) to a realistic equation we apply again the scaling hypothesis (2) [2] -[4] :

where 





In order to extent (19) to a full state-equation we apply the Padé approximant by analogy to virial expansion derived by Ree and Hoover [7] :

where

5. Estimation of the Pseudo-State Equation’s Parameters
At the beginning we have to notice that the data collected in Table 2 reveal sudden change of 


where 

6. Optimization of Technological Parameters
Function 



Formula (24) represents the minimal iso-power loss curve. All points satisfying (24) are solutions of the optimization problem for technical parameters of SMC.
7. Conclusion
By introducing the binary relations we have revealed twofold. The power loss characteristics do not cross each other which makes the topology’s set of this curves very useful and effective that we can perform all calculations in the one-dimension space spanned by the scaled frequency or here in the case of pseudo-statee quation in the scaled temperature. For general knowledge concerning such a topology we refer to the papers by Egenhofer [8] and by Nedas et al. [9] . However, to our knowledge this paper is the first one about the binary relations be-
Table 3. Somaloy 500, low-losses phase. Values of pseudo-state equation’s parameters and the Padé approximant’s coefficients of (22).
Table 4. Somaloy 500, high-losses phase. Values of pseudo-state equation’s parameters and the Padé approximant’s coefficients of (22).
Figure 4. Phase diagram for Somaloy 500.
tween magnitudes of different dimensions in the sense of different physical magnitudes. Also, this paper is the first one which presents an application of scaling in designing the technological parameters’ values by using the pseudo-state equation of SMC. The obtained result is the continuous set of points satisfying (24). All solutions of these equations are equivalent for the optimization of the power losses. Therefore, the remaining degree of freedom can be used for optimizing magnetic properties of the considered SMC. Ultimately, one must say that the degree of success achieved when applying the scaling depends on the property of the data. The data must obey the scaling.
Acknowledgements
The work has been supported by National Center of Science within the framework of research project Grant N N507 249940.
References
- Ślusarek, B., Jankowski, B., Sokalski, K. and Szczygłowski, J. (2013) Characteristics of Power Loss in Soft Magnetic Composites a Key for Designing the Best Values of Technological Parameters. Journal of Alloys and Compounds, 581, 699-704. http://dx.doi.org/10.1016/j.jallcom.2013.07.084
- Sokalski, K., Szczygłowski, J., Najgebauer, M. and Wilczy?ski, W. (2007) Losses Scaling in Soft Magnetic Materials. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 26, 640-649. http://dx.doi.org/10.1108/03321640710751118
- Sokalski, K. and Szczygłowski, J. (2009) Formula for Energy Loss in Soft Magnetic Materials and Scaling. Acta Physica Polonica A, 115, 920-924.
- Sokalski, K., Szczygłowski, J. and Wilczy?ski, W. (2013) Scaling Conception of Power Loss’ Separationin Soft Magnetic Materials. International Journal of Condensed Matter, Advanced Materials, and Superconductivity Research (NOVA), 12, Nr. 4.
- Bertotti, G. (1984) A General Statistical Approach to the Problem of Eddy Current Losses. Journal of Magnetism and Magnetic Materials, 41, 253. http://dx.doi.org/10.1016/0304-8853(84)90192-6
- Bertotti, G. (1988) General Properties of Power Losses in Soft Ferromagnetic Materials. IEEE Transactions on Magnetics, 24, 621. http://dx.doi.org/10.1109/20.43994
- Ree, F.H. and Hoover, W.G. (1964) Fifth and Sixth Virial Coefficients for Hard Spheres and Hard Disks. The Journal of Chemical Physics, 40, 939. http://dx.doi.org/10.1063/1.1725286
- Egenhofer, M. (1989) A Formal Definition of Binary Topological Relationships. In: Litwin, W. and Schek, H.J., Eds., Proceedings of the 3rd International Conference on Foundations of Data Organization and Algorithms (FODO), Paris, France, Lecture Notes in Computer Science, 367, (Springer-Verlag, New York, 1989) 457-472.
- Nedas, K.A., Egenhofer, M.J. and Wilmsen, D. (2007) Definitions of Line-Line Relations. International Journal of Geographical Information Science, 21, 21-48.
NOTES
*Corresponding author.








