Materials Sciences and Applications
Vol.4 No.4(2013), Article ID:30648,7 pages DOI:10.4236/msa.2013.44033
Determination of Residual Stresses Numerically Obtained in ASTM AH36 Steel Welded by TIG Process
![]()
Department of Mechanical Engineering, Federal University of Pernambuco, Cidade Universitária, Recife-PE, Brazil.
Email: *ras@ufpe.br
Copyright © 2013 Pablo Batista Guimarães et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 2nd, 2013; revised March 6th, 2013; accepted April 5th, 2013
Keywords: Finite Element Method; TIG Welding; Temperature Field; Residual Stresses
ABSTRACT
Residual stresses have been numerically determined in welded joints. In this study, the numerical model is based on the coupling of different physical phenomena considering the thermal, mechanical and metallurgical nature of a welding process. The ABAQUS software program was used to perform the numerical simulations, based on the finite element method (FEM). The aspects related to the mathematical modeling of complex welding procedures were pondered with the FEM: variations in the physical and mechanical properties of the materials as a function of the temperature; the transience and the speed of the welding process, the material phase transformations; the different mechanisms of heat exchange with the environment (convection and radiation); all them associated with a high level of nonlinearity. The heat source used in this analytical model for heat supply was the double ellipsoid model proposed by Goldak, in which a 60 mm × 50 mm and 3 mm rectangular ASTM AH36 steel plate was used for the TIG process simulations. Throughout this work, the optimization of the welding procedures currently practiced in petrochemical and ship building industries can be applied to reduce the levels of residual stresses.
1. Introduction
The multiplicity of phenomena affecting a welding process and their microstructural heterogeneity has been a complicating factor for the theoretical analysis and prediction of the physical and mechanical properties of welded joints. The state of residual stresses is an important factor that determines the load capacity and the lifetime of a structural element. Residual stresses greatly influence the characteristics of the mechanical strength of the structural elements, considering their development after several technological processes as well as welding, thermomechanical processes, surface or thermochemical treatments, all caused by heterogeneous plastic deformation, sometimes supported by thermal action and/or phase transformations.
Studies on residual stresses have been used to define the conditions to carry out welding operations, developing lower levels of residual stresses and reducing the development of cracks [1]. Tsirkas et al. [2] conducted simulations research to determine the temperature field in welded joints using laser welding in order to obtain further the stress field. Monin et al. [3] experimentally obtained residual stresses using X-ray diffraction.
The resulting heterogeneous and complex microstructures followed by residual stresses cause the mechanical properties of a welded joint to be harder do forecast. Residual stress has been defined as any existing tension in the volume of a material without applying any external load [4,5]. These authors have separately published studies on the consequences of the residual stresses and distortions in welded steel structures. In a review, Francis et al. [6] described how the residual stresses are generated in structures of a ferritic steel plant and the methodology for the determination of these tensions.
In this study, an experimental methodology was developed to numerically determine the residual stresses of a welded joint. This numerical model is based on the coupling of different physical phenomena of thermal, mechanical and metallurgical natures existing in a welding operation. In order to do that, an analytical heat source double ellipsoid model proposed by Goldak et al. [7] was used to model the heat input. This model can be easily adopted by the industry because the input parameters of the welding process, such as electrical current, voltage and welding speed, can be controlled.
In the fusion arc welding process, the energy is concentrated in one region of the joint where the welding is being performed while the remaining material stays at lower energy regions. Under these conditions, a complex temperature field is generated as a function of both position and time producing a non-uniform and transient (time-changing) temperature distribution. Thus, the expansion of the natural hot regions is limited by the adjacent and less heated regions, generating a non-uniform plastic deformation. These heterogeneous deformations besides the cordon are responsible for much of the residual stresses produced by the welding.
According to Gurova et al. [8] and Castello et al. [9], another factor that may lead to the development of residual stresses are the volume changes (expansion or contraction) occurring during the phase transformations in solid. These authors made monitoring of the residual stresses of welded sheets for the ship building industry and proposed a numerical model to determine the stress state employing only the effect of thermal expansion of steel as a cause of residual stresses, neglecting the phase transformations and surface cooling. In summary, according to Macherauch et al. [10] and Bhadeshia [4], the development of residual stresses in welding is due to:
• Contraction during cooling in regions that are heated and plasticized differently (heterogeneous plastic deformation);
• More intense superficial cooling;
• Phase transformation.
Changes in volume (expansion or contraction) occurring during the phase transformations in the solid state can also lead to the development of residual stresses. In steels, the austenite-ferrite transformation occurs with volume expansion which is hindered by the unprocessed welding bead neighboring regions [6]. The intensity of residual stresses in the welding bead is related to the degree of restriction of the mechanical structure, which is usually 100% in the longitudinal direction of the weld joint. Temperature variations cause plastic deformations due to the thermal expansion phenomena. The deformations are accompanied by an irreversible material yield, thus resulting in a dissipation of energy in the form of heat in the material. In a numerical model this dissipative energy must be taken into account adding one more source term to the heat equation to achieve a thermomechanical coupling. However, a 1% plastic deformation during the loading of 400 MPa rises the temperature by approximately one degree, which can be negligible considering the welding process temperature [11].
Studying the weldability of the Inconel 738 alloy, Danis [12] proposed a numerical model considering simultaneously thermal, metallurgical and mechanical effects based on welding repair of upstream guide vanes. Kerrouault [11] examined the residual stresses in austenitic stainless steel alloy to reduce hot cracking. The thermo-mechanical problem of the welding can be attributed to a weak coupling, in which the thermal problem that will serve as the load for the mechanical calculation will be solved in the first place. Under these conditions, the mechanical setting has no influence on the thermal field. Residual stresses can be obtained from the deformations generated during a welding process. These deformations can be either elastic (εEl), plastic (εPl), viscoelastic (εVE) or thermal (εT), so the total strain can be determined by Equation (1).
 (1)
(1)
2. Materials and Methods
For the simulation of residual stresses, a 60 mm × 50 mm and 3 mm rectangular ASTM AH36 steel plate was used, considering the use of a TIG (tungsten inert gas) in the welding process. Table 1 shows the chemical composition of the alloy.
Numerical simulations were performed with a software program based on the finite element method (FEM). The board was divided into elements type DC3D8 sum to a total of 18,788 elements. This mesh presented more refinement in the fusion zone and in the heat affected zone (HAZ), because those were the areas where the most important phenomena in the welding process occurred. This mesh refinement is shown in Figure 1 and in Table 2.
These elements are continuous-3D linear formulation and each one of them contains 8 nodes (Figure 2). For all elements, edges along the 0.75 mm sheet thickness were always used, remaining four elements along the thickness of the plate.
The solution to the thermal problem is given by Equation (2).
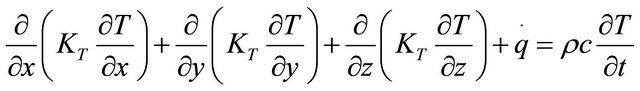 (2)
(2)
Table 1. Chemical composition of ASTM AH36 steel.

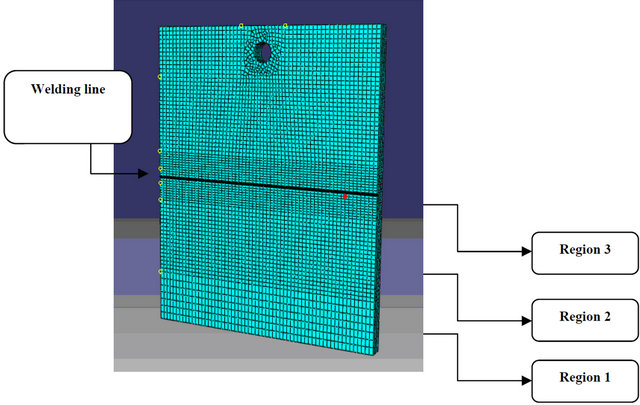
Figure 1. Mesh used for solution of the thermal and mechanical problems.
Table 2. Mesh elements for the FEM calculation.

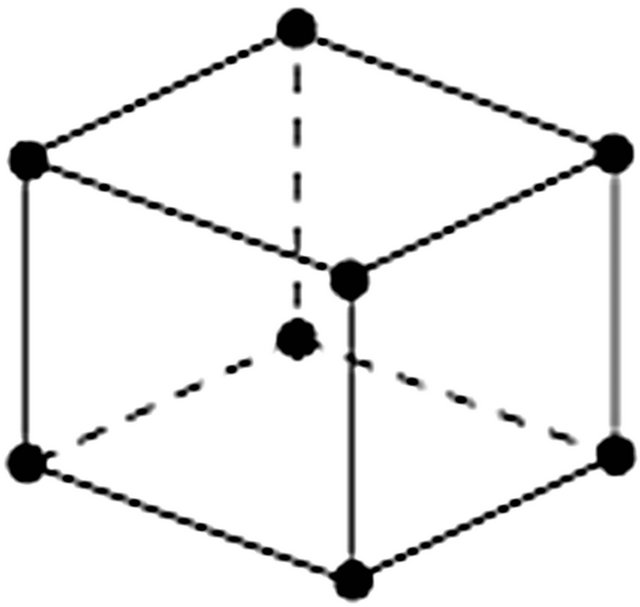
Figure 2. Element DC3D8 having 8 nodes and linear formulation [14,15].
where KT, q, ρ and c present: thermal conductivity, heat generation, density and specific heat, respectively. For the thermal boundary conditions, the exchange of convection and radiation was considered during the welding process. These boundary conditions were imported to the model. Five sides of the plate were welded, except the lower surface, which rested on the table during the welding operation. Heat exchange by convection and radiation was expressed by Equation (3) (Newton’s law) and Equation (4) (Stefan Boltzmann’s law), respectively.
 (3)
(3)
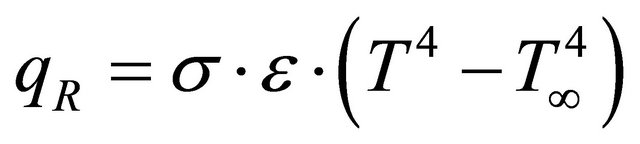 (4)
(4)
where h is the convection coefficient, σ is Stefan Boltzmann’s constant and ε represents emissivity. Literature values were used to model heat exchange and the assumed convection around the board. The ambient temperature considered was 25˚C and emissivity 0.7 [1].
The values used for the convection coefficient (h), specific heat (Cp) and thermal conductivity (kT) are shown in Figure 3 as a function of temperature [2]. The source used in this study was the double ellipsoid model proposed by Goldak, shown in Figure 4. The geometric parameters b, c were determined by metallographic analysis and the energy parameters af, ar, ff and fr were obtained with the support of the relationships found in references suggested by Gery et al. [1] and Goldak et al. [7] (Table 3). During the modeling, a FORTRAN DFLUX subroutine [15] was developed to displace the heat source. This function determines the torch position versus time, and calculates the heat input in all points of the board. Only one mechanical boundary [12,13] condition was established because the plate was attached through a 4 mm diameter hole, as shown in Figure 1.
The welding parameters [16] used in this paper are shown in Table 4.
The isotropic elasto-plastic hardening was the model used to determine residual stresses, and these strains were obtained from those generated during the welding operation. These deformations were considered elastic, plastic, and thermal in nature, so the total strain was determined by Equation (5).
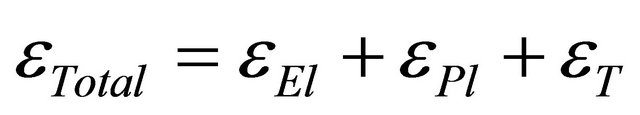 (5)
(5)
Both elastic and plastic deformations were obtained by tensile tests, and thermal deformations were obtained from the coefficient of thermal expansion as a function of temperature. Equation (6) was used.

Figure 3. Variation of material properties as a function of temperature [2].
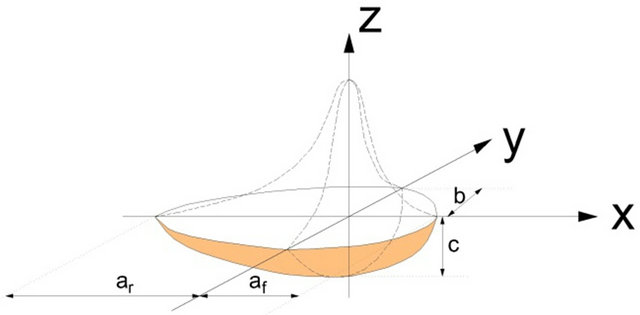
Figure 4. Schematic representation of the source of double ellipsoid.
Table 3. Geometrical parameters and energy from the heat source.

Table 4. Parameters of heat input used in the numerical simulation.

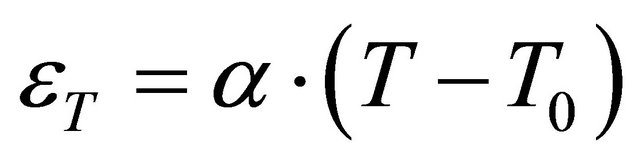 (6)
(6)
Considering that α is the expansion coefficient, T0 is the room temperature and T is the temperature of a specific point, the values of the mechanical properties as a function of the temperature [2] are shown in Figure 5.
To evaluate the results obtained by simulation the residual stresses were also measured by X-ray diffraction. A portable diffractometer was used to determine the tensions in the field. This equipment, by means of a specific software program, determines the stresses in the longitudinal and transverse directions of the welding. These stresses were determined at seven different points, as shown in Figure 6, after the sample had been submitted to a chemical cleaning with 2% Nital solution.
3. Results and Discussion
The stress field in the welding bead longitudinal direction after cooling the plate is demonstrated in Figure 7. The variation of the stresses versus time for a point 2 mm distant from the edge of welding bead is shown in Figure 8.
The welding time was 50 s and then, the piece was naturally cooled for 300 s. During welding, the stress at the welding point compared to a point 2 mm distant from the welding bead reached a minimum value of 445 MPa (compressive), then it reverts and reaches a maximum of 478 Mpa (tensile) stabilizing around 430 MPa during the cooling after 150 - 200 s. In the process of cooling, the weld metal solidified, the material contracted being hindered by regions that were cooler and more distant from the weld, giving rise to tensile stresses along the welding bead and compression stresses in more remote areas.
After total cooling, the residual stress in the center of the welding bead reached a level of the same order of magnitude of the material yield strength (430 MPa).
Figure 9 shows the behavior of the longitudinal stresses of the welded points on seven different measurements obtained by X-ray diffraction and by the numerical model. For the transverse direction (Figure 10), the same behavior was observed in relation to two measurement techniques (modeling and RX).
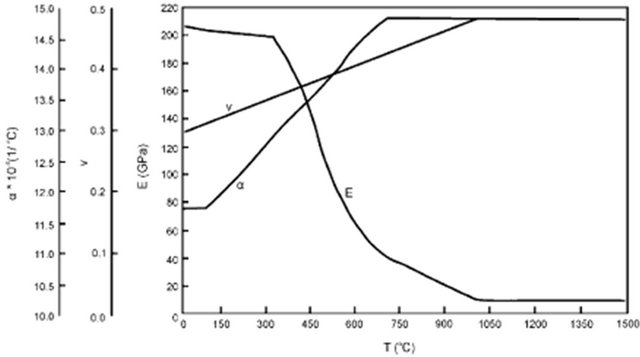
Figure 5. Variation of mechanical properties of the material [2].

Figure 6. Schematic representation of points of residual stress measured by X-ray diffraction.
The model developed with the ABAQUS software program was quite satisfactory in determining the residual stress, considering the stress measured by the X-ray behavior, which is an established method [3,17]. The model presented higher values than those experimentally measured by X-ray diffraction, because the welded plate recrystallized during cooling, after welding. The enthalpies of phase transformations were not considered by the model. In addition, it should be observed that a manual process was used; then the energy absorbed during welding was not uniform, and this had direct impact on the field under stress. The knowledge about the field where residual stresses occur in a welded joint is very important to optimize the welding procedures currently adopted in the industry, considering the reduction in the stress levels. Due to the complexity of the phenomena involved during welding, this model still needs further adjustments.
This study is just the beginning of the prediction of residual stresses, contributing to the improvement of the welding processes, particularly in establishing restricttions for the fixation of the plates during the process.
4. Conclusions
The behavior of the residual stresses in this model was consistent in terms of tensile and compressive forces; for a point 2 mm distant from the weld filet.
After cooling, the residual stresses for a point 2 mm distant from the weld filet reach levels of the same order of magnitude of the material yield strength (430 MPa).
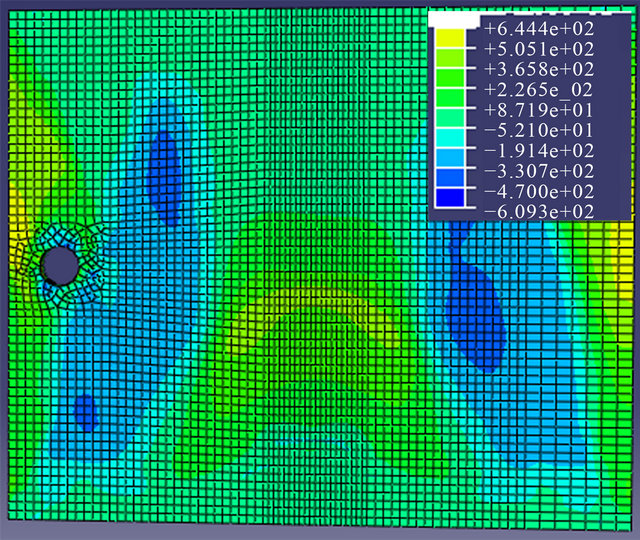
Figure 7. Range of residual stresses [MPa] in the longitudinal direction.
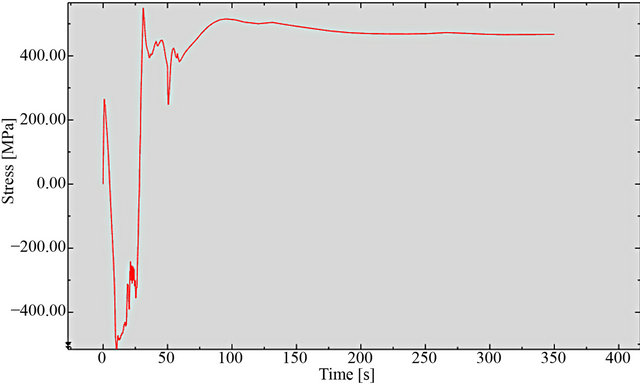
Figure 8. Longitudinal stress versus time of a point 2 mm distant from the edge of the welding bead.
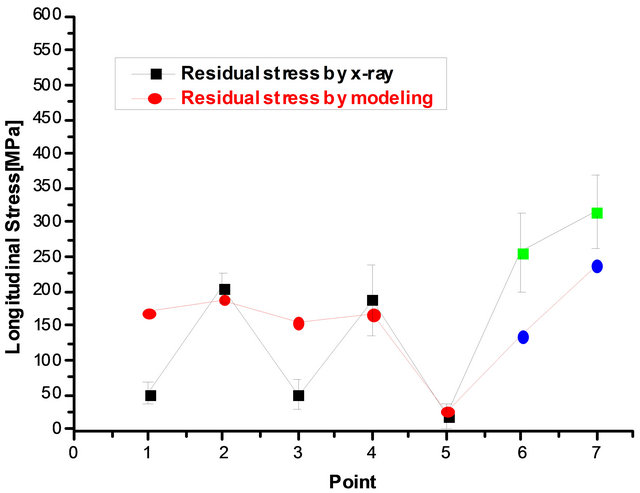
Figure 9. Comparison in performance of residual stresses in the longitudinal direction.
The determination of the temperature field in TIG welding can be simulated with ABAQUS to determine
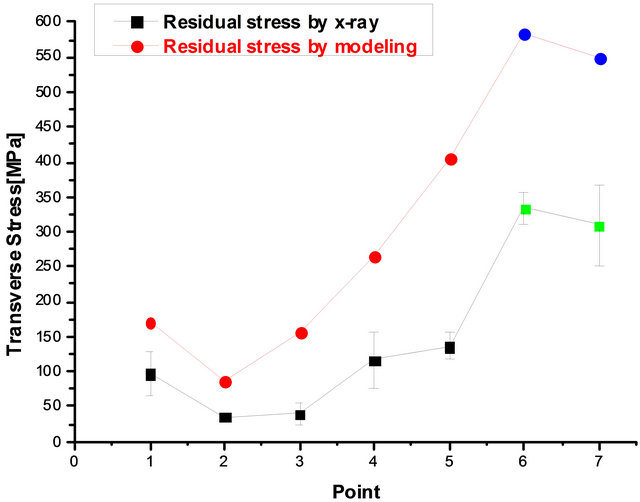
Figure 10. Comparison in performance of residual stresses in the transversal direction.
subsequent residual stresses, considering all thermomechanical effects. By observing phase transformation (γ-α) during virtual welding, this model presented results consistent with the practical experience.
5. Acknowledgements
We would like to thank FACEPE (Pernambuco State Foundation for Science and Technology) for their financial support to this study, as well as to the Federal University of Campina Grande for the X-ray measurements.
REFERENCES
- D. Gery, H. Long and P. Maropoulos, “Effects of Welding Speed Energy Input and Heat Source Distribution on Temperature Variations in Butt Joint Welding,” Journal of Materials Processing Technology, Vol. 167, No. 2-3, 2005, pp. 393-401. doi:10.1016/j.jmatprotec.2005.06.018
- S. A. Tsirkas, P. Papanikos and T. H. Termanidis, “Numerical Simulation of the Laser Welding Process in ButtJoint Specimens,” Journal of Materials Processing Technology, Vol. 134, No. 1, 2003, pp. 59-69. doi:10.1016/S0924-0136(02)00921-4
- V. I. Monin, J. R.Teodosio and T. Gurova, “A Portable X-ray Apparatus for Both Stress Measurements and Phase Analysis under Field Conditions,” Advances in X-ray Analysis, Vol. 43, 2000, pp. 66-71
- K. Masubuchi, “Analysis of Welded Structures: Residual Stress, Distortion and Their Consequences,” Pergamon Press, Oxford, 1980.
- H. K. D. H. Bhadeshia, “Developments in Martensitic and Bainitic Steels: Role of the Shape Deformation,” Materials Science and Engineering: A, Vol. 378, No. 1-2, 2004, pp. 34-39.
- J. A. Francis, H. K. D. H. Bhadeshia and P. J. Withers, “Welding Residual Stresses in Ferritic Power Plant Steels,” Materials Science and Technology, Vol. 23, No. 9, 2007, pp. 1009-1020. doi:10.1179/174328407X213116
- J. A. Goldak and M. Akhlaghi, “Computational Welding Mechanics,” Springer, New York, 2002.
- T. Gurova, F. Quaranta and S. Estefen, “Monitoramento do Estado de Tensões Residuais Durante a Fabricação de Navios,” 2008.
- X. Castello, T. Gurova and S. Estefen, “Simulação das Tensões Residuais de Chapas Soldadas na Construção Naval,” 2008.
- E. Macherauch and K. H. Kloos, “Origin Measurement and Evaluation of Residual Stresses,” Residual Stress in Science and Technology, Vol. 1, 1987, pp. 3-27.
- N. Kerrouault, “Fissuration à Chaud en Soudage d'un Acier Inoxydable austénique,” Ph.D. Thesis, Université Centrale Paris, Paris, 2000.
- Y. Danis, “Etude de la Soudabilité d'un Superalliage Base Nickel Fortement Chargé en Eléments Durcissants Titane et Aluminium: L'inconel 738,” Ph.D. Thesis, Université Bordeaux 1, Bordeaux, 2008.
- Y. Danis, E. Lacoste and C. Arvieu, “Numerical Modeling of Inconel 738LC Deposition Welding: Prediction of Residual Stress Induced Cracking,” Journal of Materials Processing Technology, Vol. 210, No. 14, 2010, pp. 2053-2061. doi:10.1016/j.jmatprotec.2010.07.027
- Hibbit, Karlsson & Sorenson Inc., “Getting Started with Abaqus: Keywords Edition, Version 6.7.,” USA, 2007.
- Hibbit, Karlsson & Sorenson Inc., User Subroutines Reference Manual: Version 6.7.,” USA, 2007.
- P. B. Guimarães, P. M. A. Pedrosa, Y. P. Yadava, J. M. A. Barbosa and R. A. S. Ferreira, “Determinação Numérica do Campo de Temperatura de uma Junta Soldada de Aço ASTM AH-36,” Proceedings of VI CONEM, Brazil, 2010.
- J. T. Assis, V. I. Monin and F. R. Pereira, “Portable Minidiffractometer for Measurements in Laboratory and Field Conditions,” The 49th Conference of Denver X-Ray, 2000.
NOTES
*Corresponding author.

