Materials Sciences and Applications
Vol.4 No.1(2013), Article ID:27077,7 pages DOI:10.4236/msa.2013.41008
First Principles Study of Structural and Electronic Properties of OxS1−xZn Ternary Alloy
![]()
1Department of Physics, University of Djillali Liabes, Sidi Bel-Abbes, Algeria; 2Institute of Nono Electronic Engineering, University Malaysia Perlis, Kangar, Malaysia; 3Modeling and Simulation Materials Sciences Laboratory, Sidi-Bel-Abbès University, Sidi Bel-Abbes, Algeria.
Email: *lttnsameri@yahoo.fr
Received September 6th, 2012; revised October 12th, 2012; accepted November 2nd, 2012
Keywords: FP-LMTO; Ab-Initio; Approach of Zunger; Effective Mass
ABSTRACT
We perform self-consistent ab-initio calculations to study the structural and electronic properties of zinc blende ZnS, ZnO and their alloy. The full-potential muffin-tin orbitals (FP-LMTO) method was employed within density functional theory (DFT) based on local density Approximation (LDA), and generalized gradient approximation (GGA). We analyze composition effect on lattice constants, bulk modulus, band gap and effective mass of the electron. Using the approach of Zunger and coworkers, the microscopic origins of band gap bowing have been detailed and explained. Discussions will be given in comparison with results obtained with other available theoretical and experimental results.
1. Introduction
The II-VI compound semiconductors have recently received considerable interest a lot of experimental and theoretical work on this alloy’s, they were promoted much interest because of their numerous applications in optoelectronic devices such as visual displays, high-density optical memories, transparent conductors, solid-state laser devices, photodetectors, solar cells, etc. for 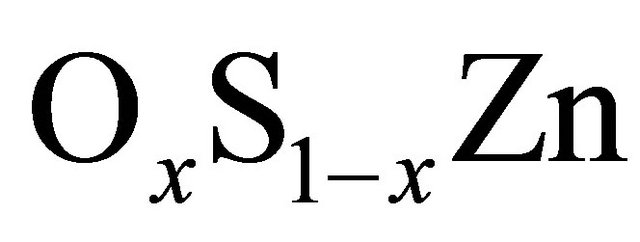 few studies that have been done on this alloy due the difficulty in the synthesis of this material, due to the large electronegativity differences between O and S [1]. From this the purpose of this paper is to illustrate such modifications by providing original ab initio structural and electronic properties for the zinc blende (ZB)
few studies that have been done on this alloy due the difficulty in the synthesis of this material, due to the large electronegativity differences between O and S [1]. From this the purpose of this paper is to illustrate such modifications by providing original ab initio structural and electronic properties for the zinc blende (ZB)  alloy with different discrete compositions, namely x = 0, 0.25, 0.50, 0.75, 1 and compare them with ZB ZnS and ZnO. The calculations were carried out within the density functional theory (DFT) [2,3]. Therefore, the main aim of the present study was to investigate the electronic and structural properties of
alloy with different discrete compositions, namely x = 0, 0.25, 0.50, 0.75, 1 and compare them with ZB ZnS and ZnO. The calculations were carried out within the density functional theory (DFT) [2,3]. Therefore, the main aim of the present study was to investigate the electronic and structural properties of  ternary alloy in cubic phase over a wide range of compositions 0 ≤ x ≤ 1 by using the full-potential muffin-tin orbitals (FP-LMTO) method. Various quantities, including lattice parameters, bulk modulus, band gap, optical bowing and effective masses, were obtained for these alloy.
ternary alloy in cubic phase over a wide range of compositions 0 ≤ x ≤ 1 by using the full-potential muffin-tin orbitals (FP-LMTO) method. Various quantities, including lattice parameters, bulk modulus, band gap, optical bowing and effective masses, were obtained for these alloy.
The organization of this paper is as follows: we explain the FP-LMTO computational method in Section 2. In Section 3, the results and discussion for structural and electronic properties are presented. Finally, a conclusion is given in Section 4.
2. Computational Methods
The calculations reported in this work were carried out by FP-LMTO [4,5] within the density functional theory DFT based on local density Approximation LDA [6] and generalized gradient approximation GGA [7]. In this method the space is divided into an interstitial region (IR) and non-overlapping muffin-tin (MT) spheres centered at the atomic sites. In the IR region, the basis functions are represented by Fourier series. Inside the muffin-tin spheres, the basis sets is described by radial solutions of the one-particle Schrödinger equation (at fixed energy) and their energy derivatives multiplied by spherical harmonics. The valence wave functions inside the spheres are expanded up to lmax = 6. The k integration over the Brillouin zone is performed using the tetrahedron method [8]. The values of the sphere radii (MTS) and the number of plane waves (NPLW) used in our calculation are listed in Table 1.
3. Results and Discussion
3.1. Structural Properties
The calculations were firstly carried out to determine the structural properties of ZB binary compounds ZnS and ZnO and 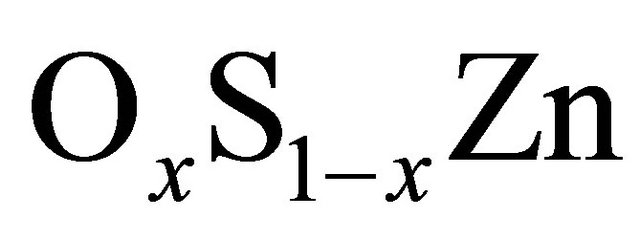 alloys. To model the
alloys. To model the  ZB structure alloys, we applied a 8-atom supercell. For the considered structures and at different oxygen concentrations x (x = 0, 0.25, 0.50, 0.75, 1), the structural properties were obtained by a minimization of total energy as a function of the volume for ZnS, ZnO and
ZB structure alloys, we applied a 8-atom supercell. For the considered structures and at different oxygen concentrations x (x = 0, 0.25, 0.50, 0.75, 1), the structural properties were obtained by a minimization of total energy as a function of the volume for ZnS, ZnO and  in the ZB structure. The bulk modulus and their pressure derivatives were obtained by a non-linear fit of the total energy versus volume according to the Birche-Murnaghan’s equation of state [9]. In Table 2, we summarize the calculated modulus and their pressure derivatives) of ZnS, ZnO compounds and
in the ZB structure. The bulk modulus and their pressure derivatives were obtained by a non-linear fit of the total energy versus volume according to the Birche-Murnaghan’s equation of state [9]. In Table 2, we summarize the calculated modulus and their pressure derivatives) of ZnS, ZnO compounds and 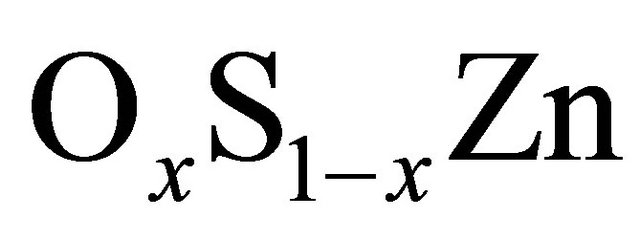 alloys. Considering the general trend that the GGA usually overestimates the lattice parameters while LDA is expected to underestimates them [10], It is clear that our results are in reasonable agreement with experimental values and theoretical results. Usually, in the treatment of alloys, it is assumed that the atoms are located at the ideal lattice sites and the lattice constant varies linearly with composition x according to the so-called Vegard’s law [30].
alloys. Considering the general trend that the GGA usually overestimates the lattice parameters while LDA is expected to underestimates them [10], It is clear that our results are in reasonable agreement with experimental values and theoretical results. Usually, in the treatment of alloys, it is assumed that the atoms are located at the ideal lattice sites and the lattice constant varies linearly with composition x according to the so-called Vegard’s law [30].
Table 1. The plane wave number PW, energy cuttof (in Ry) and the muffin-tin radius (RMT) (in a.u.) used in calculation for binary ZnS and ZnO and their alloy in zinc blende (ZB) structure.

aRef. [16], bRef. [20].
Table 2. Lattice constants a, bulk modulus B, and pressure derivative of bulk modulus B, for ZB ZnS, ZnO and OxS1−xZn solid solutions.
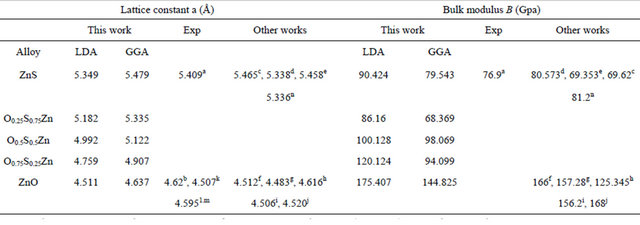
aRef. [11], bRef. [12], cRef. [13], dRef. [14], eRef. [15], fRef. [16], gRef. [17], hRef. [18], iRef. [19], jRef. [20], kRef. [21], lRef. [22], mRef. [23], nRef. [24].
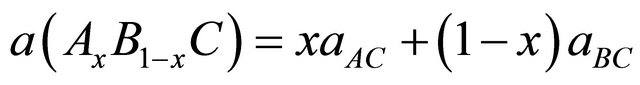 (1)
(1)
where aAC and aBC are the equilibrium lattice constants of the binary compounds AC and BC Hence, the lattice constant can be written as:
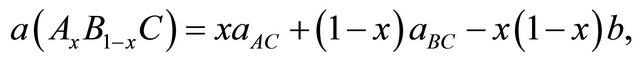 (2)
(2)
where the quadratic term b is the bowing parameter.
Figures 1 and 2 show the variation of the calculated equilibrium lattice constant and the bulk modulus versus concentration for 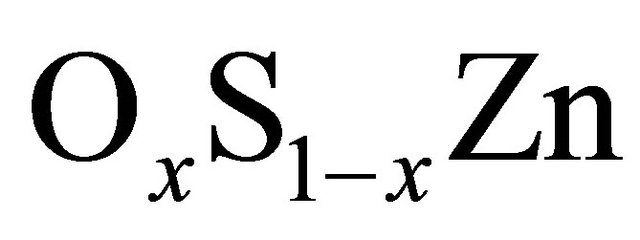 alloy. A slight large deviation from Vegard’s law [30] is clearly visible for the
alloy. A slight large deviation from Vegard’s law [30] is clearly visible for the 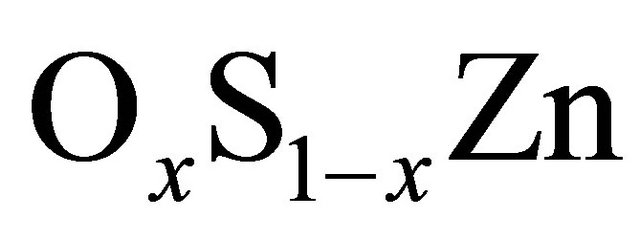 alloy. The bowing parameter determined by LDA, are obtained by fitting the calculated values respectively,
alloy. The bowing parameter determined by LDA, are obtained by fitting the calculated values respectively,  is the alloy lattice constant. With a polynomial function we found an upward and downward bowing parameter equal to −0.2359 Å and 142.9979 GPa for lattice and bulk modulus. The GGA results are −0.2887 Å and 142.9981 GPa. The physical origin of this slight large deviation could be mainly due to the large size difference between the O and S atom and the mismatch of the lattice constants of ZnS and ZnO compound.
is the alloy lattice constant. With a polynomial function we found an upward and downward bowing parameter equal to −0.2359 Å and 142.9979 GPa for lattice and bulk modulus. The GGA results are −0.2887 Å and 142.9981 GPa. The physical origin of this slight large deviation could be mainly due to the large size difference between the O and S atom and the mismatch of the lattice constants of ZnS and ZnO compound.
3.2. Electronic Properties
The calculations of the electronic band structure properties, magnitude of band-gap were carried out for ZnS, ZnO and  in ZB structure at the equilibrium calculated lattice constants. The band-gaps calculated using the FP-LMTO method for ZB ZnS, ZnO and
in ZB structure at the equilibrium calculated lattice constants. The band-gaps calculated using the FP-LMTO method for ZB ZnS, ZnO and 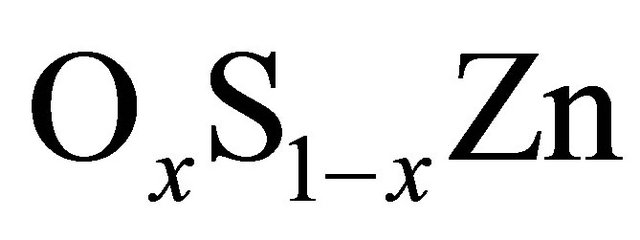 are listed in Table 3 for the high-symmetry
are listed in Table 3 for the high-symmetry
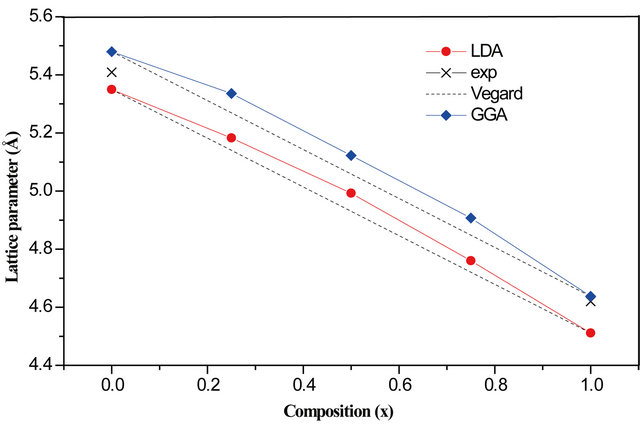
Figure 1. Composition dependence of the calculated lattice constants using the GGA (solid squares) and LDA (solid circles) for 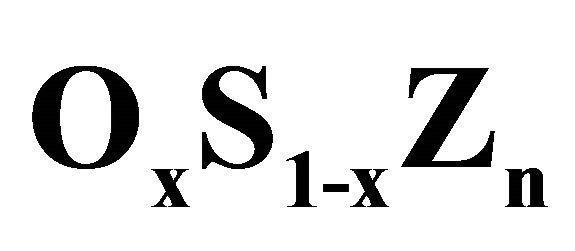 alloy compared with Vegard’s law (dashed line).
alloy compared with Vegard’s law (dashed line).

Figure 2. Composition dependence of the calculated bulk modulus using the LDA (solid squares) and GGA (solid circles) of 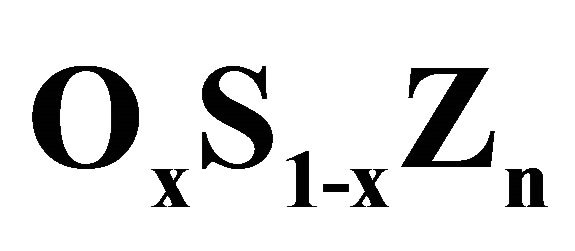 alloy.
alloy.
points Γ and X in the Brillouin zone. All energies are with reference to the top of the valence band at Γ point. The results show that ZnS and ZnO compound is a direct-gap semiconductor with the minimum of conduction band at Γ point.The calculated GGA (LDA) energy gaps of ZnS and ZnO Eg are 1.97(2.12) eV and 0.69(0.79) eV, respectively, which are in good agreement with the theoretical values as listed in Table 3. Focusing now on the electronic properties of the 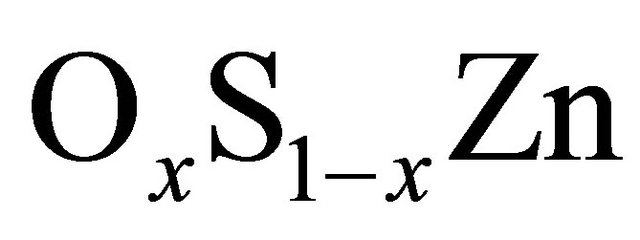 alloy system we obtained the direct band-gap at Γ point. Figure 3 presents the variation of the direct and indirect band gap energies as functions of the composition x for the ternary alloys. We note direct (Γ-Γ) and indirect (Γ-X) band gap not intersect because the computed band structures of the alloys using both LDA and GGA schemes indicate a direct band gap at various concentrations.
alloy system we obtained the direct band-gap at Γ point. Figure 3 presents the variation of the direct and indirect band gap energies as functions of the composition x for the ternary alloys. We note direct (Γ-Γ) and indirect (Γ-X) band gap not intersect because the computed band structures of the alloys using both LDA and GGA schemes indicate a direct band gap at various concentrations.
Indeed it is a general trend to describe the bandgap of an alloy AxB1−xC in terms of the pure compound energy gap EAC and EBC by the sem-empirical formula:
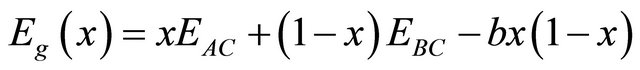 (3)
(3)
where EAC and EBC corresponds to the gap of the ZnO and ZnS for the OxS1−xZn alloy. The calculated band gap versus concentration was fitted by a polynomial equation. The results are shown in Figure 3 and are summarized as follows
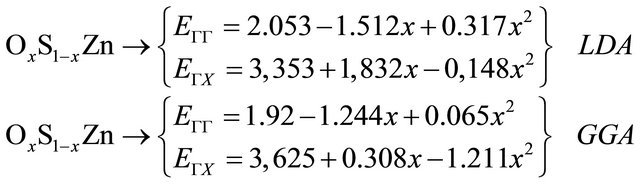 (4)
(4)
In order to better understand the physical origins of the large and composition-dependent bowing in  alloy alloys, we follow the procedure of Bernard and Zunger [31] and decompose the total bowing parameter b into physically distinct contributions. The overall bowing
alloy alloys, we follow the procedure of Bernard and Zunger [31] and decompose the total bowing parameter b into physically distinct contributions. The overall bowing
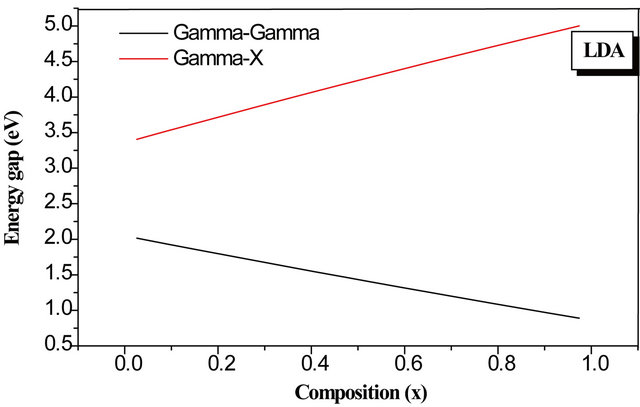
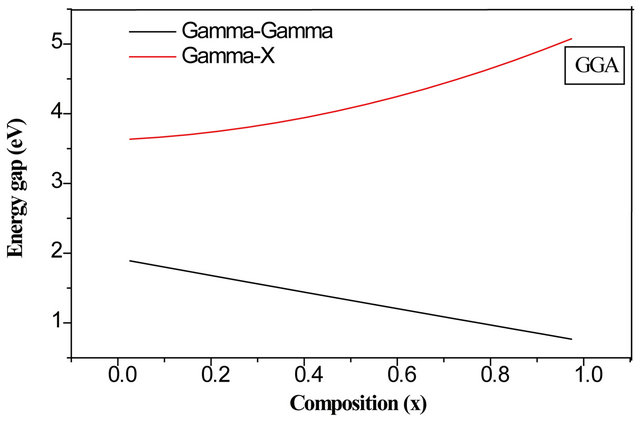
Figure 3. Direct and indirect band gap energies as a function of O composition using the LDA and GGA of  alloy.
alloy.
Table 3. Direct (Γ–Γ) and indirect (Γ–X) band gaps of ZnS and ZnO and their alloy at equilibrium volume (The energy is given in eV).
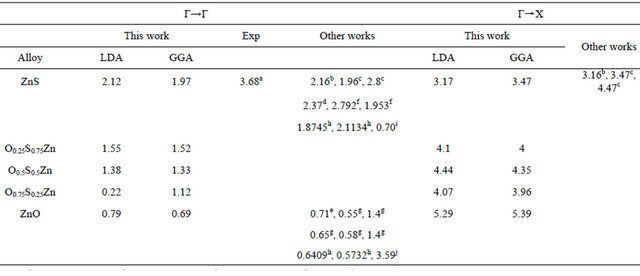
aRef. [25], bRef. [14], cRef. [15], dRef. [26], eRef. [16], fRef. [13], gRef. [18], hRef. [27], iRef. [19], jRef. [28].
coefficient at a given average composition x measures the change in band gap according to the formal reaction.
 (5)
(5)
where aAC and aBC are the equilibrium lattice constants of the binary compounds. which aeq is the equilibrium lattice constant of the alloy with the average composition x.
We decompose reaction into three step:
 (6)
(6)
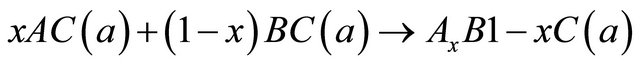 , (7)
, (7)
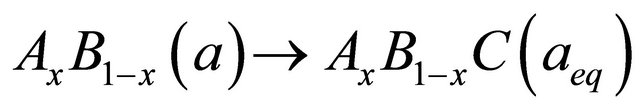 . (8)
. (8)
The first contribution, the volume deformation (bVD) represents the relative response of the band structure of the binary compounds AC and BC to hydrostatic pressure. The second contribution, the charge-exchange (CE) contribution bCE, reflects a charge-transfer effect that is due to the different (averaged) bonding behavior at the lattice constant a. The final step measures by bSR, changes due to the structural relaxation (SR) in passing from the unrelaxed to the relaxed alloy. Consequently, the total gap bowing parameter is defined as
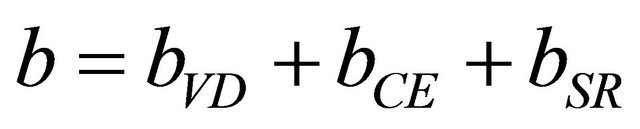 . (9)
. (9)
The general representation of the composition-dependent band gap of the alloys in terms of binary compounds gaps of the, 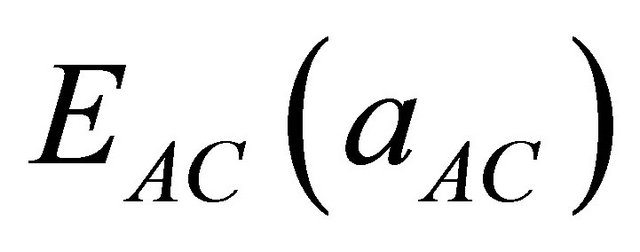 and
and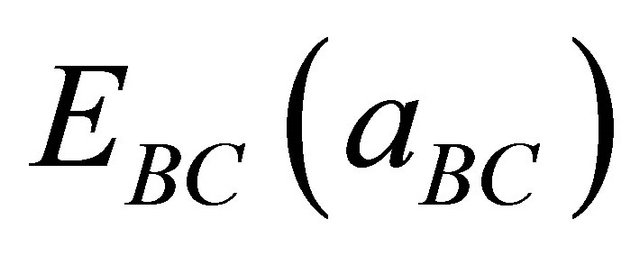 , and the total bowing parameter b is
, and the total bowing parameter b is
 (10)
(10)
where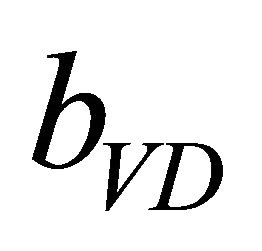 ,
, 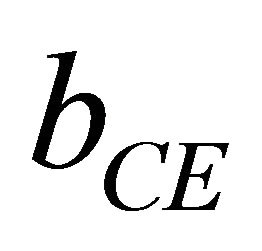 and
and 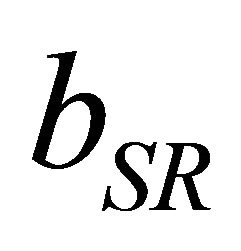 represents respectively the volume deformation (VD) effect, the charge exchange (CE) contribution and the structural relaxation (SR) of the alloy according to the following expressions:
represents respectively the volume deformation (VD) effect, the charge exchange (CE) contribution and the structural relaxation (SR) of the alloy according to the following expressions:
 , (11)
, (11)
 , (12)
, (12)
 . (13)
. (13)
The addition of the three contributions (11), (12), and (13) leads to the total bowing parameter b. The computed bowing coefficients b together with the three different contributions for the band gaps as a function of the molar fraction (x = 0.25, 0.5 and 0.75) are shown in the Table 4. The calculated band gap bowing parameter exhibits a strong composition dependence, as calculated within the GGA and LDA calculations, which show a weakly composition dependent bowing parameter. The variation of the band gap bowing versus concentration shown in Figure 4. The bowing remains linear and Decreases rapidly from x = 0.25 to x = 0.75 in both approaches (GGA and LDA). The calculated GGA and LDA gap bowing for  alloy ranges from 0.69 eV, 1.25 eV (x = 0.25) to −0.59 eV, −0.55 eV (x = 0.75), a negligible volume deformation term
alloy ranges from 0.69 eV, 1.25 eV (x = 0.25) to −0.59 eV, −0.55 eV (x = 0.75), a negligible volume deformation term  was registered for
was registered for 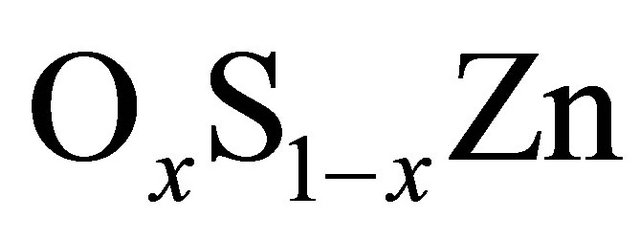 system can be correlated to the large mismatch of the lattice constants of the corresponding binary compounds between ZnS and ZnO. The charge transfer contribution bCE has been found greater than
system can be correlated to the large mismatch of the lattice constants of the corresponding binary compounds between ZnS and ZnO. The charge transfer contribution bCE has been found greater than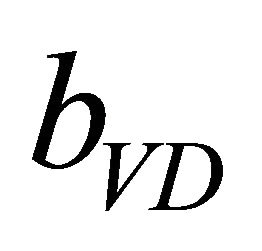 . This contribution is due to the different electronegativities of the O and S or Zn atoms. Indeed,
. This contribution is due to the different electronegativities of the O and S or Zn atoms. Indeed,  scales with the electronegativity mismatch. The contribution of the structural relaxation
scales with the electronegativity mismatch. The contribution of the structural relaxation 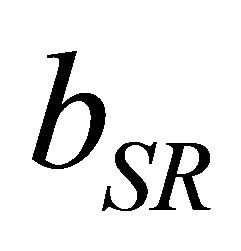 is small, the band gap bowing is due essentially charge exchange effect.
is small, the band gap bowing is due essentially charge exchange effect.
Table 4. Decomposition of optical bowing into VD, CE and SR contributions compared with other prediction.


Figure 4. Composition dependence of the calculated band gap bowing parameter using LDA (Solid Square) and GGA (Solid Circle).
Table 5. Electron (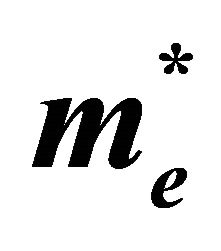 ) light hole (
) light hole (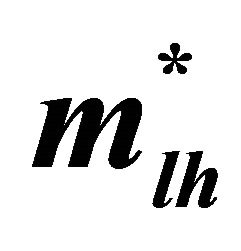 ) and heavy hole (
) and heavy hole ( ) effective masses (in units of free electron mass
) effective masses (in units of free electron mass ) at the
) at the  point of the Brillouin zone of the ternary alloys under investigation compared with the available experimental and theoretical predictions.
point of the Brillouin zone of the ternary alloys under investigation compared with the available experimental and theoretical predictions.

aRef. [29], bRef. [14], cRef. [13],dRef. [27], eRef. [15].
3.3. Effective Masses
It is also interesting to discuss at the end of the band structure study the effective masses of electrons and holes, which are important for the excitonic compounds. We have calculated the effective masses of electrons and holes using both LDA and GGA schemes are mentioned in Table 5. A theoretical effective mass in general turns out to be a tensor with nine components. However, for a very idealized simple case where E(k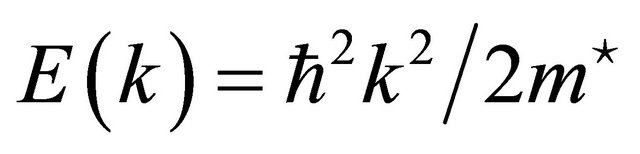 is a parabola at k = 0 (high symmetry point Γ) the effective mass becomes a scalar.
is a parabola at k = 0 (high symmetry point Γ) the effective mass becomes a scalar.
4. Conclusion
In summary, we have studied the electronic, structural properties of  alloys by using the FP-LMTO method. We found a slight large deviation from Vegard’s law for the lattice constant of
alloys by using the FP-LMTO method. We found a slight large deviation from Vegard’s law for the lattice constant of . The physical origin of this effect should be mainly due to the significant mismatch between the lattice constants of ZnS and ZnO compounds. Particular attention has been paid to the gap bowing, which exhibits linear behaviour versus the concentration. In addition, we have computed the effective masses of the electron (hole), which increases with the composition x. Our results are compared to other theoretical and experiment values.
. The physical origin of this effect should be mainly due to the significant mismatch between the lattice constants of ZnS and ZnO compounds. Particular attention has been paid to the gap bowing, which exhibits linear behaviour versus the concentration. In addition, we have computed the effective masses of the electron (hole), which increases with the composition x. Our results are compared to other theoretical and experiment values.
REFERENCES
- K. Iwata, P. Fons, A. Yamada, H. Shibata, K. Matsubara, K. Nakahara, T. Takasu and S. Niki, “Bandgap Engineering of ZnO Using Se,” Physica Status Solidi (b), Vol. 229, No. 2, 2002, pp. 887-890. doi:10.1002/1521-3951(200201)229:2<887::AID-PSSB887>3.0.CO;2-G
- P. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Physical Review, Vol. 136, No. 3B, 1964, pp. B864- B871. doi:10.1103/PhysRev.136.B864
- W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review A, Vol. 140, No. 4A, 1965, pp. A1133-A1138.
- S. Savrasov and D. Savrasov, “Full-Potential Linear-Muffin-Tin-Orbital Method for Calculating Total Energies and Forces,” Physical Review B, Vol. 46, No. 19, 1992, pp. 12181-12195. doi:10.1103/PhysRevB.46.12181
- S. Y. Savrasov, “Linear-Response Theory and Lattice Dynamics: A Muffin-Tin-Orbital Approach,” Physical Review B, Vol. 54, No. 23, 1996, pp. 16470-16486. doi:10.1103/PhysRevB.54.16470
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review B, Vol. 45, No. 13, 1992, pp. 13244-13249. doi:10.1103/PhysRevB.45.13244
- J. P. Perdew, S. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- P. Blochl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223-16233. doi:10.1103/PhysRevB.49.16223
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences USA, Vol. 30, No. 9, 1944, pp. 244-247. doi:10.1073/pnas.30.9.244
- A. Mokhtari and H. Akbarzadeh, “Electronic and Structural Properties of β-Be3N2,” Physica B: Condensed Matter, Vol. 324, No. 1-4, 2002, pp. 305-311. doi:10.1016/S0921-4526(02)01416-3
- O. Madelung, Ed., “Londolt-Bornstein,” New Series III, Vol. 22, Springer, Berlin, 1987.
- W. H. Bragg and J. A. Darbyshire, Joint Management Entrance Test, Vol. 6, 1954, p. 238.
- Z. Charifi, F. El Haj Hassan, H. Baaziz, S. Khosravizadeh, S. J. Hashemifar and H. Akbarzadeh, “Structural and Electronic Properties of the Wide-Gap Zn1−xMgxS, Zn1−xMgxSe and Zn1−xMgxTe Ternary Alloys,” Journal of Physics: Condensed Matter, Vol. 17, No. 44, 2005, pp. 7077-7088. doi:10.1088/0953-8984/17/44/001
- M. Ameri, D. Rached, M. Rabah, F. El Haj Hassan, R. Khenata and M. Doui-Aici, “First Principles Study of Structural and Electronic Properties of BexZn1–xS and BexZn1–xTe Alloys,” Physica Status Solidi (B), Vol. 245, No. 1, 2006, pp. 106-113. doi:10.1002/pssb.200743128
- H. Baaziz, Z. Charifi, F. El Haj Hassan, S. J. Hashemifar, and H. Akbarzadeh, “FP-LAPW Investigations of Zn1-xBexS, Zn1-xBexSe and Zn1-xBexTe Ternary Alloys,” Physica Status Solidi (B), Vol. 243, No. 6, 2006, p. 1296.
- Y. Z. Zhu, G. D. Chen and H. G. Ye, “Electronic Structure and Phase Stability of MgO, ZnO, CdO, and Related Ternary Alloys,” Physical Review B, Vol. 77, No. 24, 2008. doi:10.1103/PhysRevB.77.245209
- D. Maouche, F. S. Saoud and L. Louail, “Dependence of Structural Properties of ZnO on High Pressure,” Materials Chemistry and Physics, Vol. 106, No. 1, 2007, pp. 11- 15. doi:10.1016/j.matchemphys.2007.05.029
- A. S. Mohammadi, S. M. Baizaee and H. Salehi, “Density Functional Approach to Study Electronic Structure of ZnO Single Crystal,” World Applied Sciences Journal, Vol. 14, No. 10, 2011, pp. 1530-1536.
- H.-L. Shi and Y. Duan, “Band-Gap Bowing and P-Type Doping of (Zn, Mg, Be)O Wide-Gap Semiconductor Alloys: A First-Principles Study,” The European Physical Journal B , Vol. 66, No. 4, 2008, pp. 439-444. doi:10.1140/epjb/e2008-00448-6
- B. Amrani, I. Chiboub, S. Hiadsi, T. Benmessabih and N. Hamdadou, “Structural and Electronic Properties of ZnO under High Pressures,” Solid State Communications, Vol. 137, No. 7, 2006, pp. 395-399. doi:10.1016/j.ssc.2005.12.020
- O. Madelung, “Semiconductor: Data Handbook,” 3rd Edition, Springer, New York, 2003.
- S.-K. Kim, S.-Y. Jeong and C.-R. Cho, “Structural Reconstruction of Hexagonal to Cubic ZnO Films on Pt/Ti/SiO2/Si Substrate by Annealing,” Applied Physics Letters, Vol. 82, No. 4, 2003, p. 562. doi:10.1063/1.1536253
- A. Ashrafi and C. Jagadish, “Review of Zincblende ZnO: Stability of Metastable ZnO Phases,” Journal of Applied Physics, Vol. 102, No. 7, 2007, p. 71101. doi:10.1063/1.2787957
- H. Y. Wang, J. Cao, X. Y. Huang and J. M. Huang, “Pressure Dependence of Elastic and Dynamicalproperties of Zinc-Blende ZnS and ZnSefrom First Principle Calculation,” Condensed Matter Physics, Vol. 15, No 1, 2012, pp. 1-10.
- H. Okuyama, Y. Kishita and A. Ishibashi, “Quaternary Alloy Zn1-xMgxSySe1-y,” Physical Review B, Vol. 57, No. 4, 1998, pp. 2257-2263. doi:10.1103/PhysRevB.57.2257
- S.-G. Lee and K. J. Chang, “First-Principles Study of the Structural Properties of MgS-, MgSe-, ZnS-, and ZnSeBased Superlattices,” Physical Review B, Vol. 52, No. 3, 1995, pp. 1918-1925. doi:10.1103/PhysRevB.52.1918
- S. Zh. Karazhanov, P. Ravindrana, A. Kjekhus, H. Fjellvag, U. Grossner and B. G. Svensson, “Electronic Structure and Band Parameters for ZnX (X = O, S, Se, Te),” Journal of Crystal Growth, Vol. 287, No. 1, 2006, pp. 162-168. doi:10.1016/j.jcrysgro.2005.10.061
- M. Oshikiri and F. Aryasetiawan, “Band Gaps and Quasiparticle Energy Calculations on ZnO, ZnS, and ZnSe in the Zinc-Blende Structure by the GW Approximation,” Physical Review B, Vol. 60, No. 15, 1999, pp. 10754- 10757. doi:10.1103/PhysRevB.60.10754
- H. Kukimoto, S. Shionoya, T. Koda and T. Hioki, “Infrared Absorption Due to Donor States in ZnS Crystals,” Journal of Physics and Chemistry of Solids, Vol. 29, No. 6, 1968, pp. 935-944. doi:10.1016/0022-3697(68)90228-X
- L. Vegard, “Formation of Mixed Crystals by Solid-Phase Contact,” Journal of Physics, Vol. 5, No. 5, 1921, pp. 393-395.
- J. E. Bernard and A. Zunger, “Optical Bowing in Zinc Chalcogenide Semiconductor Alloys,” Physical Review B, Vol. 34, No. 8, 1986, pp. 5992-5995. doi:10.1103/PhysRevB.34.5992
NOTES
*Corresponding author.

