Materials Sciences and Applications
Vol.3 No.3(2012), Article ID:18063,6 pages DOI:10.4236/msa.2012.33028
The Role of Valence Electron Concentration on the Structure and Properties of Rapidly Solidified Sn-Ag Binary Alloys
![]()
1Metal Physics Lab., Physics Department, Faculty of Science, Mansoura University, Mansoura, Egypt; 2Physics Department, Faculty of Science, Port Said University, Port Said, Egypt.
Email: tnelashram@gmail.com
Received October 28th, 2011; revised December 2nd, 2011; accepted January 15th, 2012
Keywords: Alloys; Rapid Solidification; Valence Electron Concentration; Resistivity; Young’s Modulus; Fermi Energy; Brillouin Zone
ABSTRACT
A group of binary Sn-xAg alloys (x = 0.5, 1.5, 2.5, 3.5, 4.5, 5.5 and 6.5 wt%) has been produced by a single copper roller melt-spinning technique. In this study the interaction between Fermi sphere and Brillouin zone and HumeRothery condition of phase stability have been verified. It is found that by increasing valence electron concentration VEC the diameter of Fermi sphere 2kF increases which leads to the increase in the diameter of Brillouin zone which arises from the decrease in volume of the unit cell. It is found that the electrical resistivity increases by increasing VEC due to the decrease in relaxation time t with increasing VEC. Also it has been confirmed that the correlation between Young’s modulus and the axial ratio c/a of b-Sn unit cell.
1. Introduction
Valence electron concentration (VEC) plays an important role on the structure and properties of alloys. This quantity indicates the number of all valence electrons in the alloy per number of atoms. Hume-Rothery found that definite structures of compounds arise in certain ranges of the valence electron concentration [1]. These compounds are called Hume-Rothery compounds or electron compounds. Also [2,3] found that the axial ratio c/a of the β-Sn tetragonal unit cell increases by increasing VEC and decreases by decreasing VEC. This observation is confirmed recently by [4]. The increase in the axial ratio with decreasing VEC was explained qualitatively by [2,5] on the basis of the interaction between Fermi surface and Brillouin zone. When the Brillouin zone boundary touches the Fermi sphere, the structure corresponding to the zone will be stabilized. As a result, a pseudo-gap of density of states around the Fermi level will arise. This is the HumeRothery condition of phase stability i.e., KB = 2kF where KB is the diameter of Brillouin zone and kF is the radius of Fermi sphere. Also it is found by [6] that the most important factor for the formation of stable quasicrystals is the valence electron concentration.
Fermi parameters such as Fermi energy EF, radius of Fermi sphere kF Fermi velocity vF, and the diameter of the Brillouin zone KB can be calculated from the following equations;
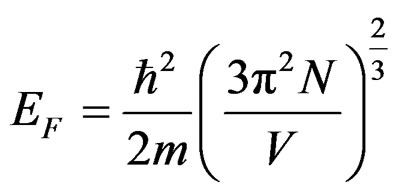 ,
, 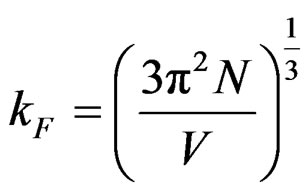 ,
, 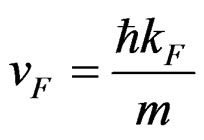 ,
, 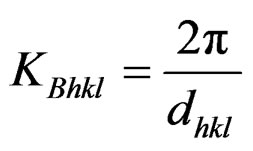
where N/V is the total number of electrons per unit volume in the alloy, m is the effective mass, ħ is the reduced Plank’s constant and dhkl is the interplanar distance.
Another example of the importance of VEC is the connection which has been observed by [4,7] between Young’s modulus and the axial ratio c/a of the tetragonal unit cell of b-Sn in which Young’s modulus increases by increasing the axial ratio. Also it is found that the resistivity decreases by increasing c/a. Therefore the objective of the present work is to study the role of valence electron concentration on the structure and properties of rapidly solidified Sn-Ag binary alloys using single roller melt-spinning technique. Rapid solidification has been used in the present work to prevent rejection of extra solute atoms and thus prevent precipitation, from a solid solution.
2. Experimental Procedures
A group of binary Sn-xAg alloys (x = 0.5, 1.5, 2.5, 3.5, 4.5, 5.5 and 6.5 wt%) have been produced by a single copper roller melt-spinning technique.
Required quantities of the used metals were weighed out and melted in a porcelain crucible. After the alloys were molten, the melt was thoroughly agitated to effect homogenization. The casting was done in air at a melt temperature of 800˚C. The speed of the copper wheel was fixed at 2900 r.p.m. which corresponds to a linear speed of 30.4 m·s–1. X-ray diffraction analysis is carried out with a Shimadzu x-ray diffractometer (DX-30), using Cu-Ka radiation with a Ni-filter (l = 0.154056 nm). Differential thermal analysis (DTA) is carried out in a Shimadzu DT-50 with heating rate 10 K/min. The measurement of resistivity is carried out by the double bridge method [8]. Young’s modulus was measured by the dynamical resonance method [9]. Vickers microhardness number (HV) is measured using the FM-7 microhardness tester.
3. Results and Discussion
3.1. Structure
Figure 1 shows the x-ray diffraction patterns for asquenched melt-spun Sn-Ag alloys. The structure of Sn- 0.5Ag alloy is single solid solution of Ag in Sn (Figure 1(a)). The solid solubility of Ag in Sn for conventional method is about 0.02 wt% at room temperature according to the equilibrium phase diagram [10]. This means extension of solid solubility from 0.02 to 0.5 wt% Ag. The Ag atoms are trapped in Sn lattice in excess of equilibrium concentration due rapid solidification. For Sn- 1.5Ag alloy an intermetallic compound Ag3Sn is formed (Figure 1(b)). From 2.5 to 5.5 wt% Ag the number and intensity of peaks due to intermetallic compound Ag3Sn increase which means that its proportion increases (Figures 1(c)-(f)). The intermetallic compound Ag3Sn is orthorhombic with space group (Pmmn) and lattice parameters a = 5.968 A, b = 4.7802 and c = 5.1843 A.
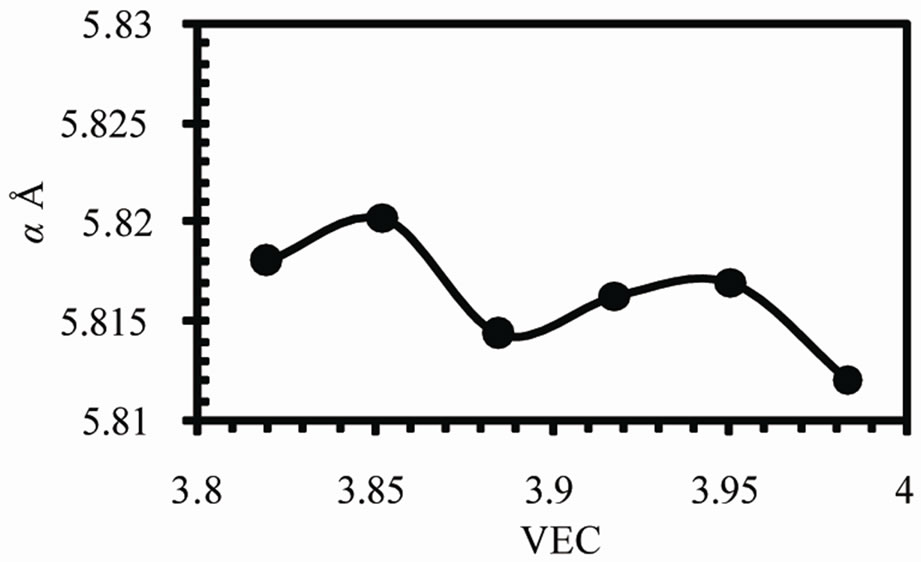
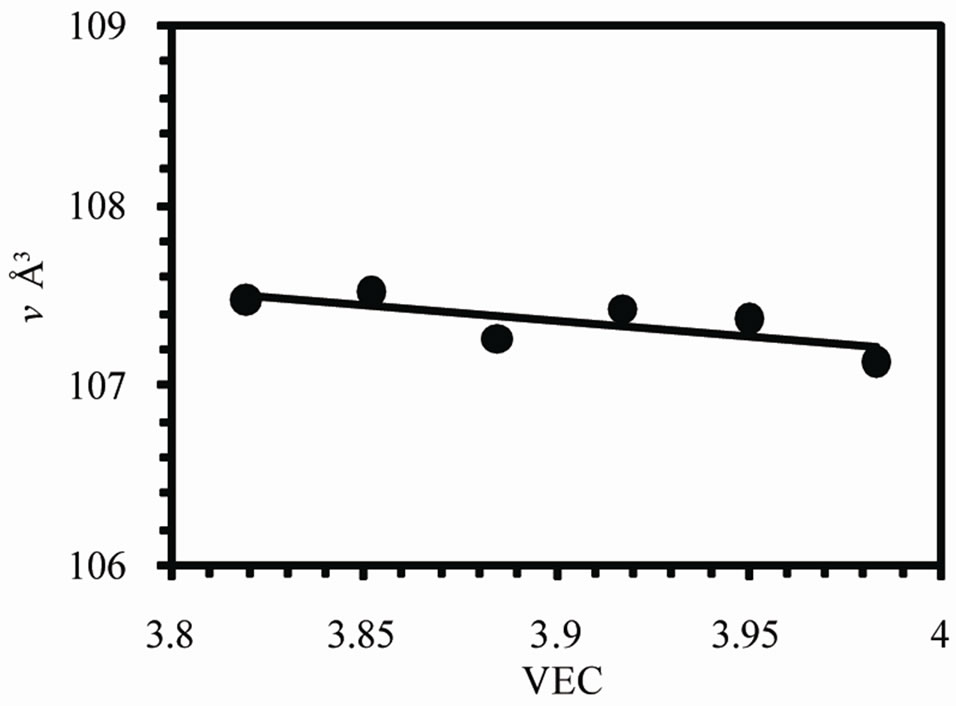
Figure 2 shows the variation of lattice parameters a, c and the axial ratio c/a of the b-Sn matrix with valence electron concentration VEC. The variation in a and c occurs in such a way to keep v decreases by increasing VEC as shown in Figure 3(a). The axial ratio c/a has a maximum value at VEC = 3.917 and minimum value at 3.852.
Figure 3(a) shows the variation of volume of unit cell v with VEC. It is found that the volume of unit cell decreases by increasing VEC (see also Table 1). Figure 3(b) shows the variation of the intensity ratio from (101) to (200) planes I101/I200 of b-Sn matrix with VEC. It is found that the ratio decreases to a minimum value 0.341 at 3.917 and then increases to maximum value about 1.8 at 3.983. The value of I101/I200 for pure Sn was found to
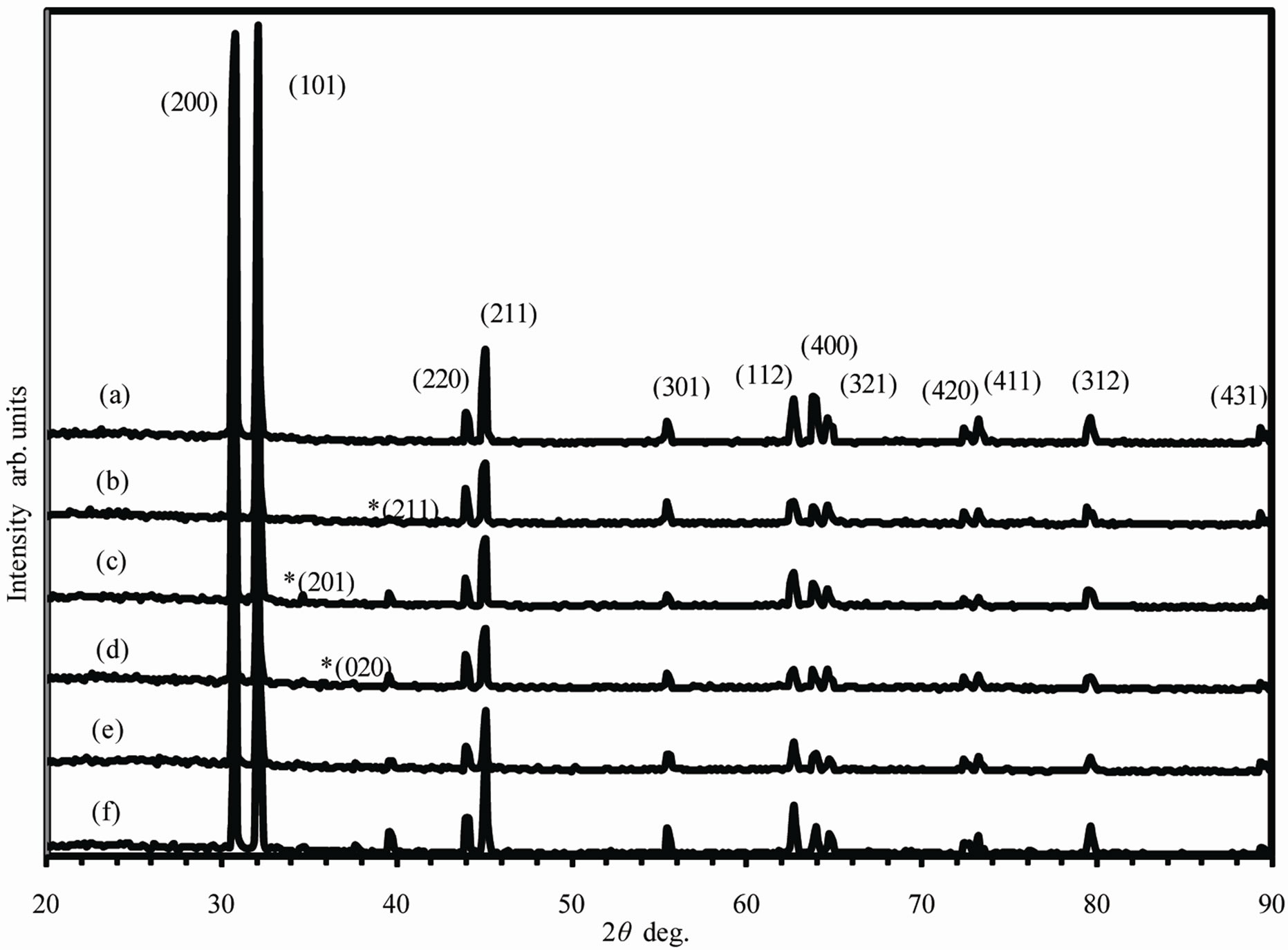
Figure 1. X-ray diffraction pattern for as quenched melt spun (a) Sn-0.5Ag; (b) Sn-1.5Ag; (c) Sn-2.5Ag; (d) Sn-3.5Ag; (e) Sn-4.5Ag; (f) Sn-5.5Ag alloys. All peaks are for b-Sn and the peaks for Ag3Sn are indicated by *.
 (a)
(a)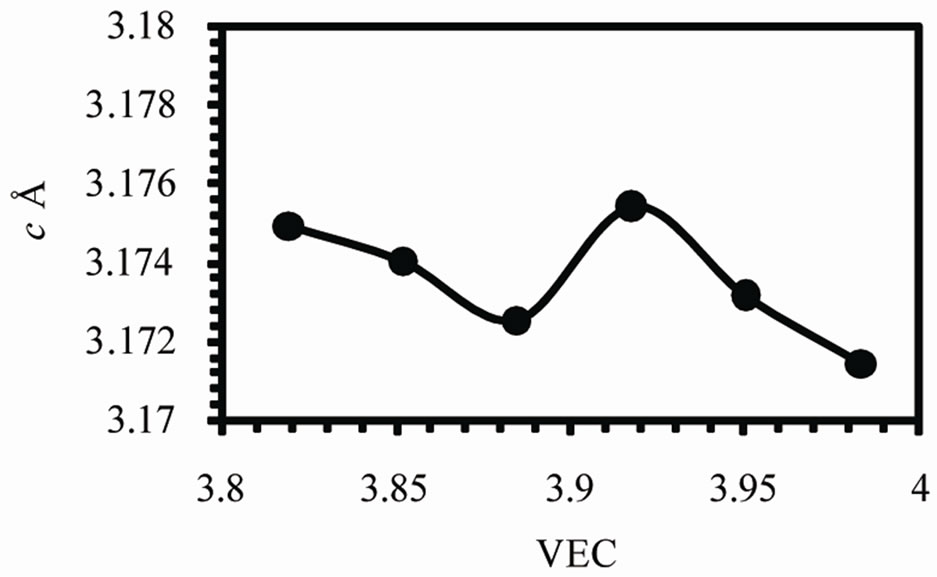 (b)
(b)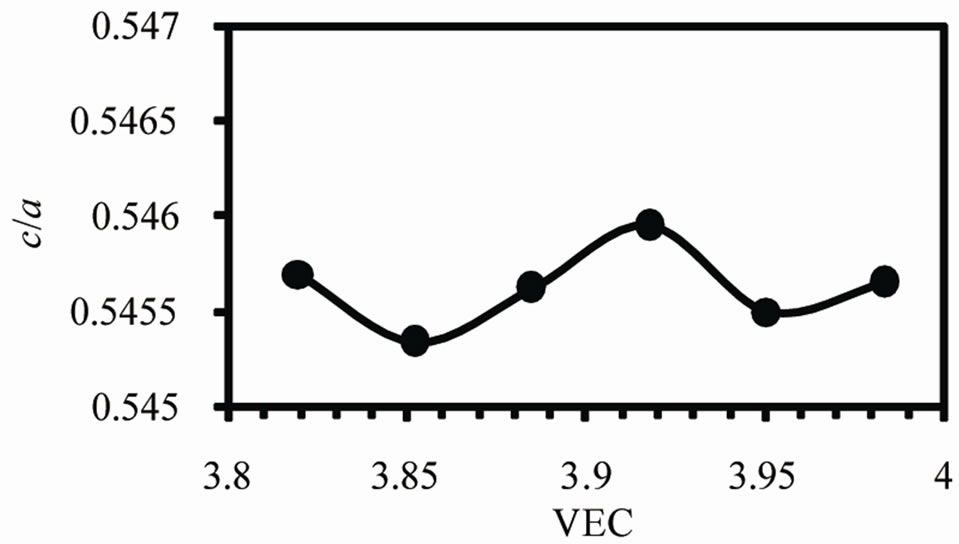 (c)
(c)
Figure 2. The variations of lattice parameters (a) a, (b) c and (c) the axial ratio c/a.
be 1.1 [11]. The addition of 0.5 Ag raises this value to 1.8; this may be attributed to that the Ag atoms are trapped in Sn lattice in excess of equilibrium concentration. The decrease in I101/I200 to 0.341may be due to the precipitation of Ag to form the intermetallic compound Ag3Sn.
The relationship between the diameter of the Brillouin zone KB and the diameter of the Fermi sphere 2kF is shown in Figure 4. A linear correlation is found between KB and 2kF. As 2kF increases, KB increases in agreement of the condition of stability (see also Table 1). The value of KB is calculated for (211) planes. This is direct evidence on the interaction between Fermi sphere and Brillouin zone and verification of Hume-Rothery condition of phase stability. From Table 1 it is clear that as the Ag concentration increases, VEC decreases since the valency of Ag is +1. All of the Fermi parameters decrease by decreasing VEC and vice versa. The decrease in v with increasing VEC means that the volume of the first Brillouin zone increases by increasing VEC since they are inversely proportional to each other. This is also indicated by the increase in KB with increasing VEC. There-
 (a)
(a) (b)
(b)
Figure 3. The variation of (a) volume of unit cell (v) and (b) intensity ratio from (101) and (200) planes (I101/I200) with VEC.

Table 1. The Fermi parameters and the diameter of the Brillouin zone.
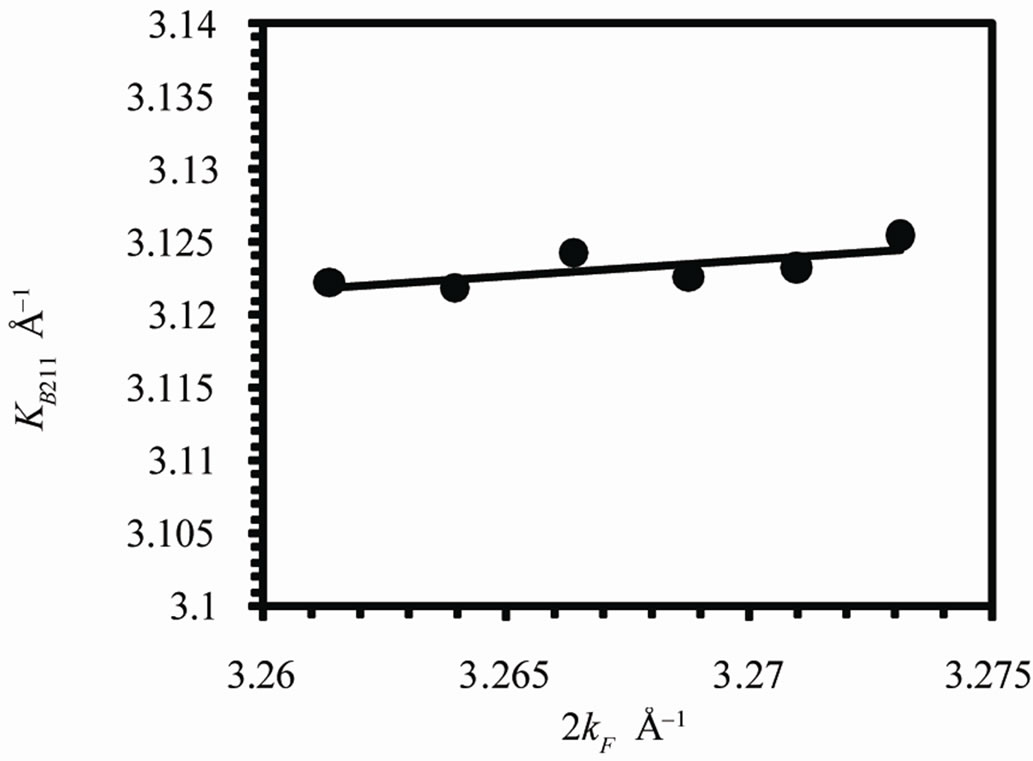
Figure 4. The relationship between the diameter of the Brillouin zone KB and the diameter of the Fermi sphere 2kF.
fore by increasing VEC the diameter of Fermi sphere increases which leads to the increase of the diameter of Brillouin zone which arises from the decrease in volume of the unit cell.
3.2. Thermal Analysis
The DTA curves obtained for as-quenched melt-spun Sn-xAg alloys (x = 0.5, 1.5, 2.5, 3.5, 4.5 and 5.5 wt%) are shown in Figure 5. There is double peak in case of Sn-0.5Ag and Sn-1.5Ag alloys. This double peak may be due to the decomposition of the supersaturated solid solution of Ag in Sn which is formed due to rapid solidification. The variation of the enthalpy ∆H of fusion with valence electron concentration VEC is shown in Figure 6" target="_self"> Figure 6(a). ∆H decreases by increasing VEC i.e., ∆H increases with Ag concentration. A maximum value 76.82 × 103 J·kg–1 is observed for VEC = 3.85 and then ∆H decreases with VEC to a minimum value 28.81 × 103 J·kg–1 for VEC = 3.95. The increase in enthalpy is due to the increase in the proportion of Ag3Sn intermetallic compound and this increases the incoherent interfaces which in turns increase the interfacial energy and hence increasing the enthalpy. The solidus Ts and liquidus T1 temperatures are shown in Figure 6(b). It is evident that the Sn-3.5Ag alloy is the eutectic alloy because it has the lowest melting point. Also the eutectic reaction is found to occur at about 494 K.
3.3. Electrical Properties
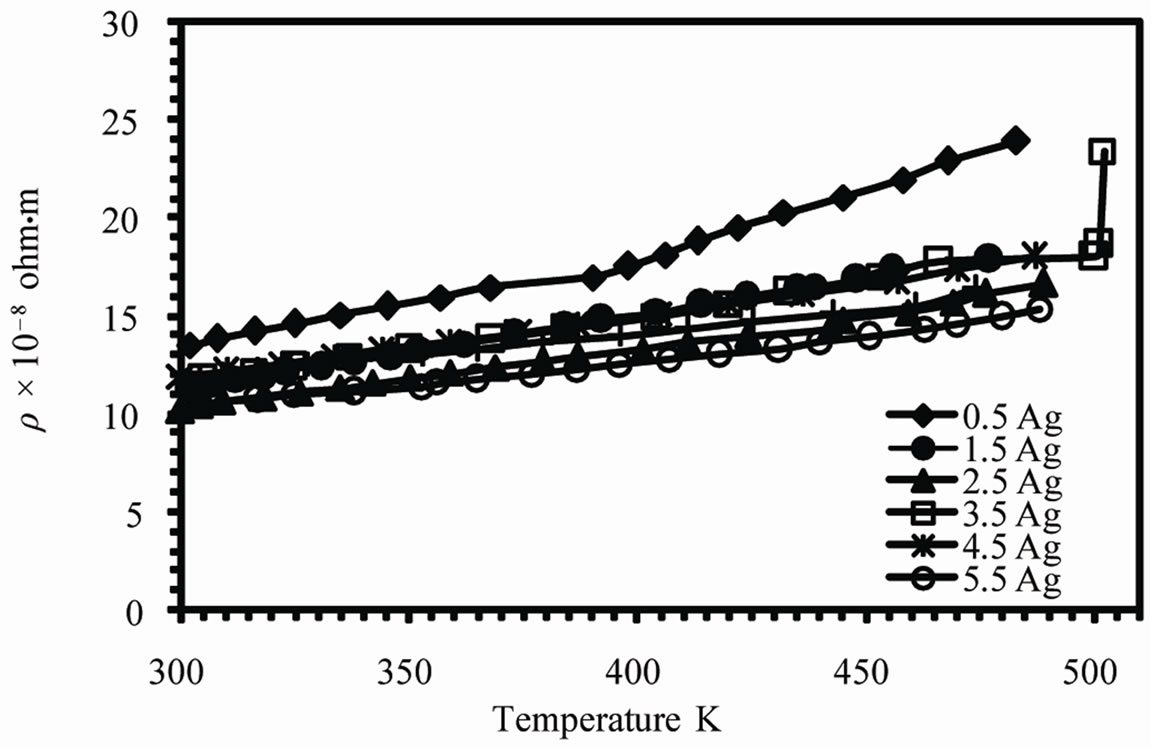
The temperature dependence of the electrical resistivity (r) of as-quenched melt-spun alloys is shown in Figure 7 (a). The resistivity increases linearly with temperature however; there is a phase transition before melting in case of Sn-0.5Ag alloy in agreement with DTA results. Also a rapid increase in resistivity observed for 3.5 Ag alloy at about 494 K which is due melting of alloy. The variation of the resistivity at room temperature with valence electron concentration (VEC) is shown in Figure 7 (b). The resistivity increases with VEC from about 9.9 × 10–8 to 12 × 10–8 ohm·m. The resistivity is given by;
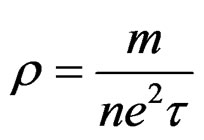 where m is the effective mass, n is the number of electrons per unit volume, e is the electron charge, and t is relaxation time. The relaxation time is given by;
where m is the effective mass, n is the number of electrons per unit volume, e is the electron charge, and t is relaxation time. The relaxation time is given by;
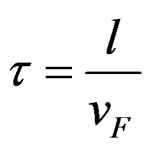 , where l is the mean free path and vF is the Fermi velocity. From Table 1 it is clear that vF increases with VEC, so that t decreases with VEC. Therefore the resis-
, where l is the mean free path and vF is the Fermi velocity. From Table 1 it is clear that vF increases with VEC, so that t decreases with VEC. Therefore the resis-
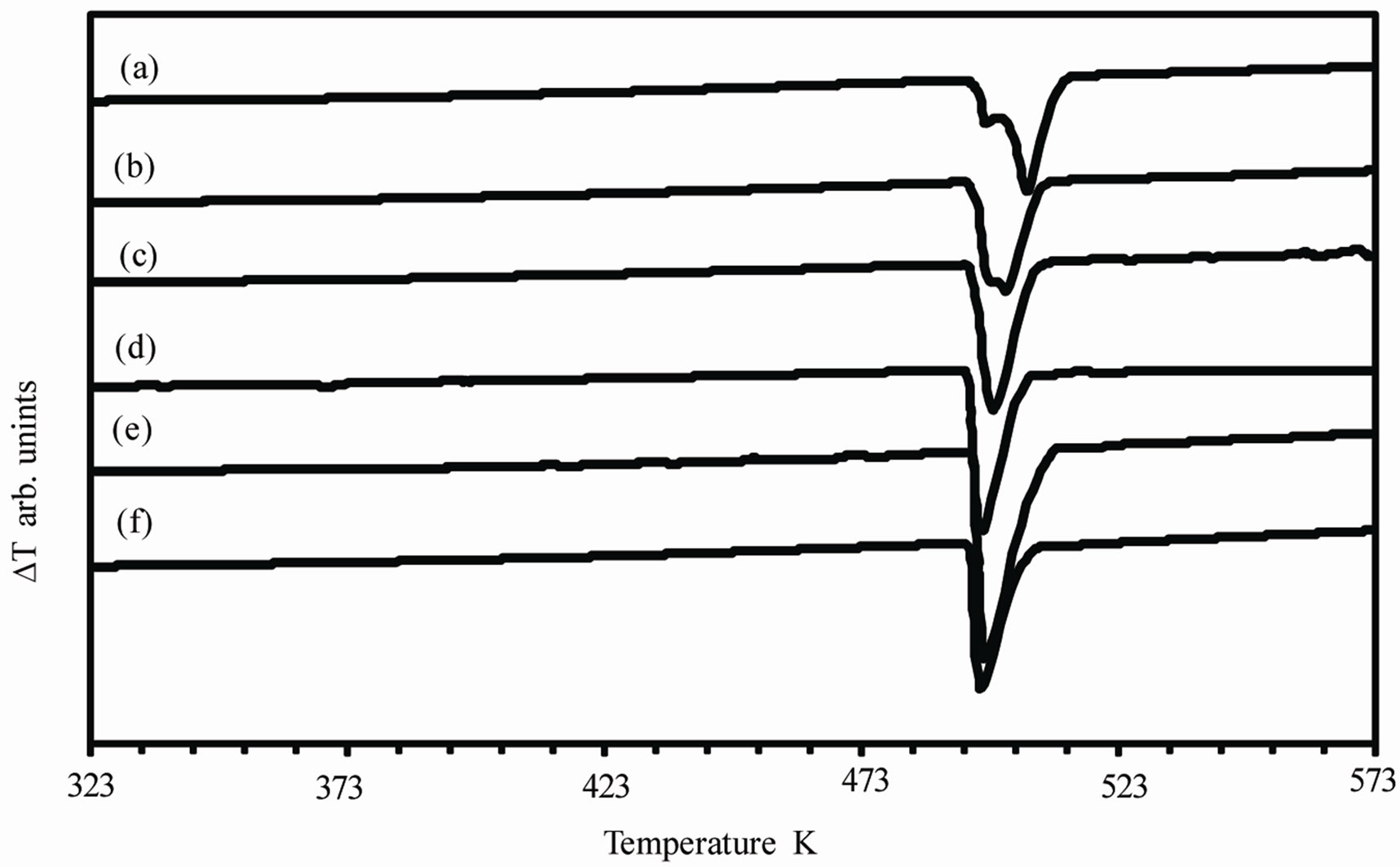
Figure 5. Differential thermal analysis for as quenched melt spun (a) Sn-0.5Ag; (b) Sn-1.5Ag; (c) Sn-2.5Ag; (d) Sn-3.5Ag; (e) Sn-4.5Ag; (f) Sn-5.5Ag alloys.
 (a)
(a)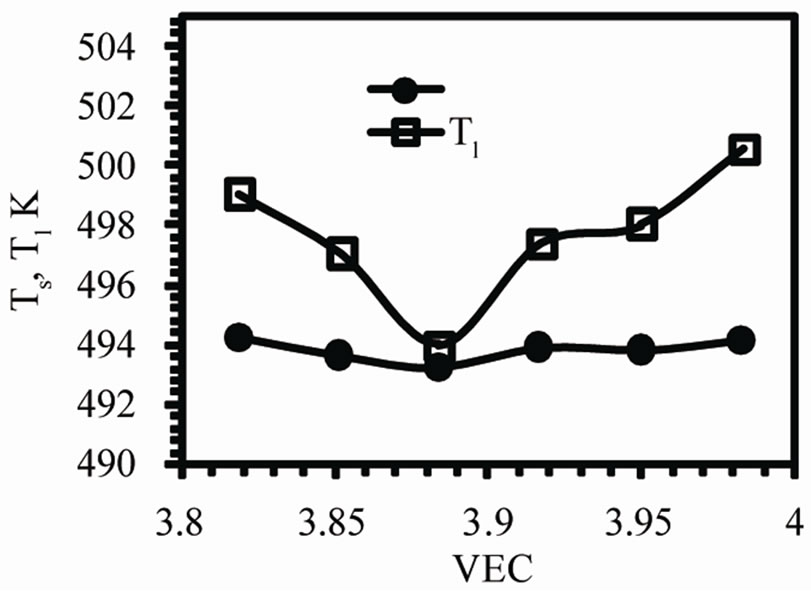 (b)
(b)
Figure 6. The variation of (a) enthalpy of fusion, (b) solidus and liquidus temperatures with VEC.
tivity increases with VEC which is observed experimentally.
Figure 7(c) shows the variation of temperature coefficient of resistivity a with VEC. It is found that a increases linearly with increasing VEC. It is well known that the relaxation time is inversely proportional to the temperature which leads to the linear dependence of the resistivity with temperature. Therefore as the relaxation time decreases with VEC, a increases with VEC.
3.4. Mechanical Properties
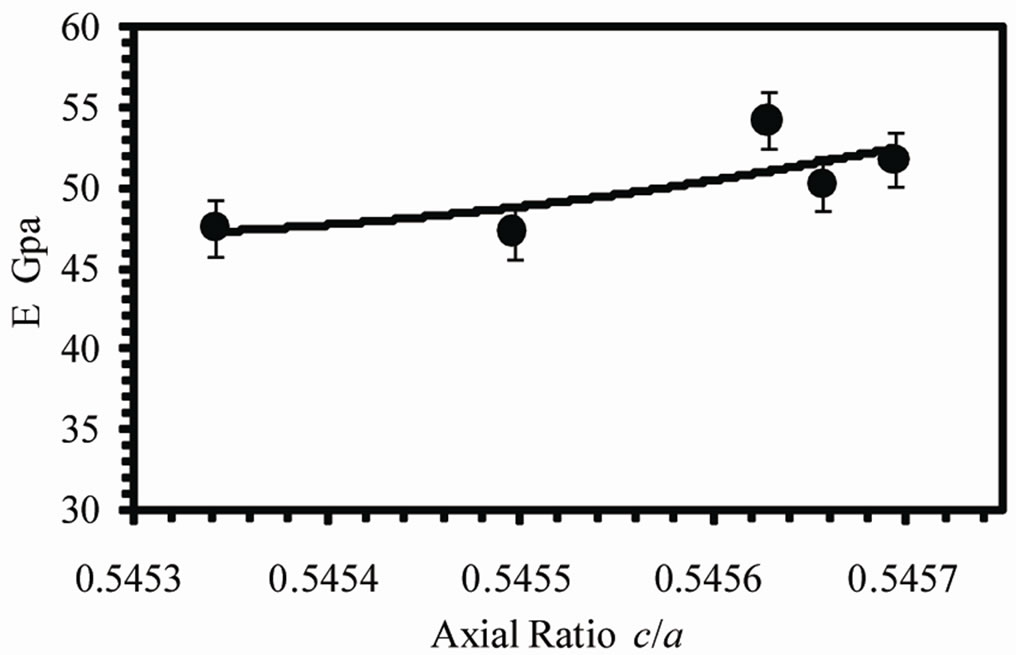
Figure 8(a) shows the variation of Young’s modulus (E) with the variation of the axial ratio (c/a) of the b-Sn matrix. It is evident that E increases by increasing c/a from 47.56 GPa at 0.5453 to 54.22 GPa at 0.5456. This result is in agreement with the result obtained by [4]. The increase in c/a ratio means the stretching of the unit cell along the c-axis, this modification in the shape of unit cell of Sn matrix may results in an increase in the bond strength which results in an increase of Young’s modulus.
Figure 8(b) shows the variation of internal friction Q–1 with the axial ratio (c/a). Q–1 decreases from 0.2138 at 0.5453 to 0.0962 at 0.5456. There are several mechanisms by which internal friction results such as thermoelastic effect, motion of interstitial and substitutional atoms, intercrystalline thermal current and the motion of dislocations. Which of these mechanisms is operative
 (a)
(a)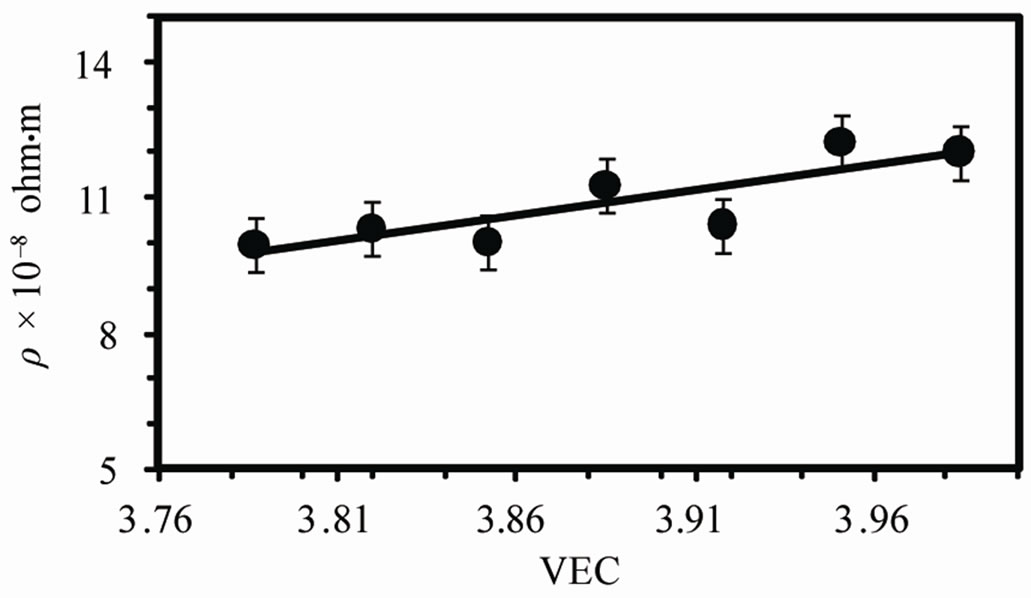 (b)
(b)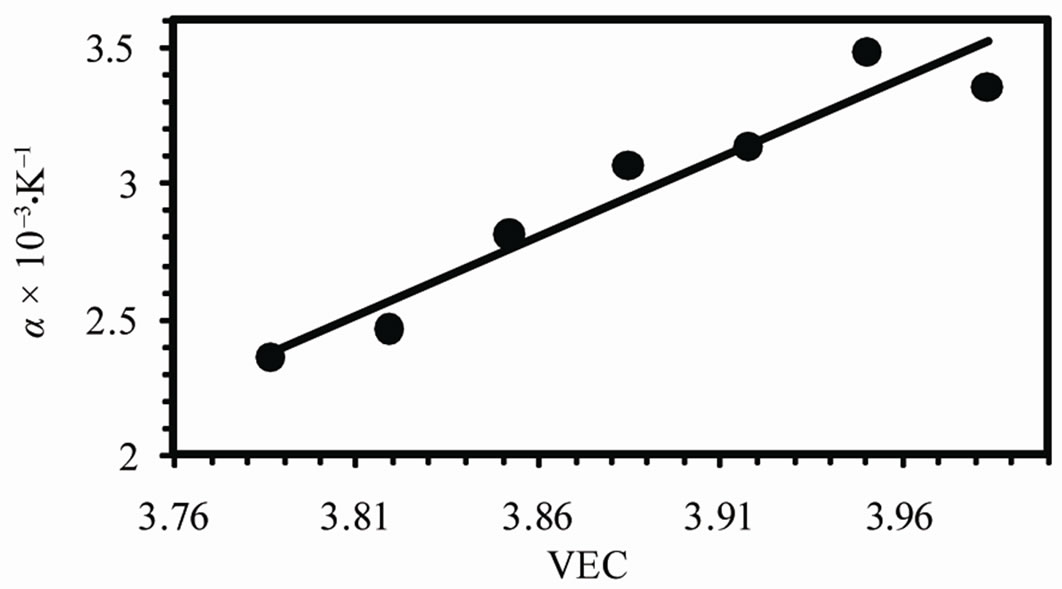 (c)
(c)
Figure 7. (a) The temperature dependence of resistivity (b) The varaition of resistivity at room temperature and (c) temperature coefficient of resistivity with VEC.
depends on the frequency. In the frequency range from 0.1 to 20 Hz used in the present work the mechanism inherent here is the motion of interstitial atoms. The decrease in internal friction with c/a may be due to the stretching of the unit cell along c-axis resists the movement of Ag atoms within the unit cell.
Figure 8(c) shows the variation of Vickers microhardness number HV with VEC. It is found that HV decreases with increasing VEC from 167 MPa to a minimum value 93 MPa and then increases to 117 MPa at 3.9835. This means HV increases by increasing Ag concentration. The increase in HV due to the addition of Ag is attributed to the dispersion hardening of small particles
 (a)
(a)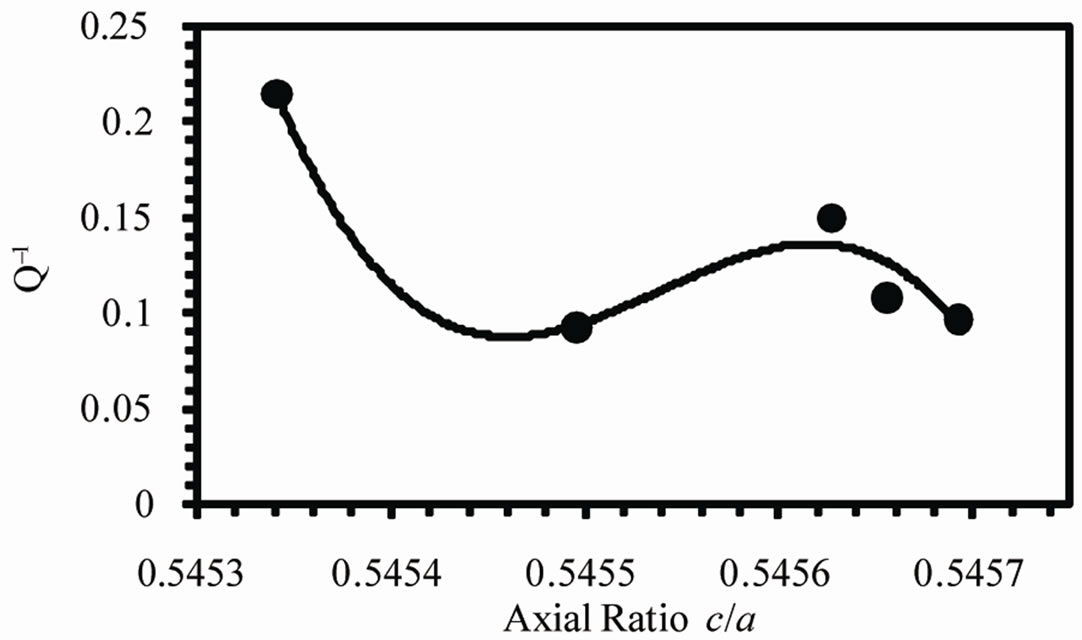 (b)
(b)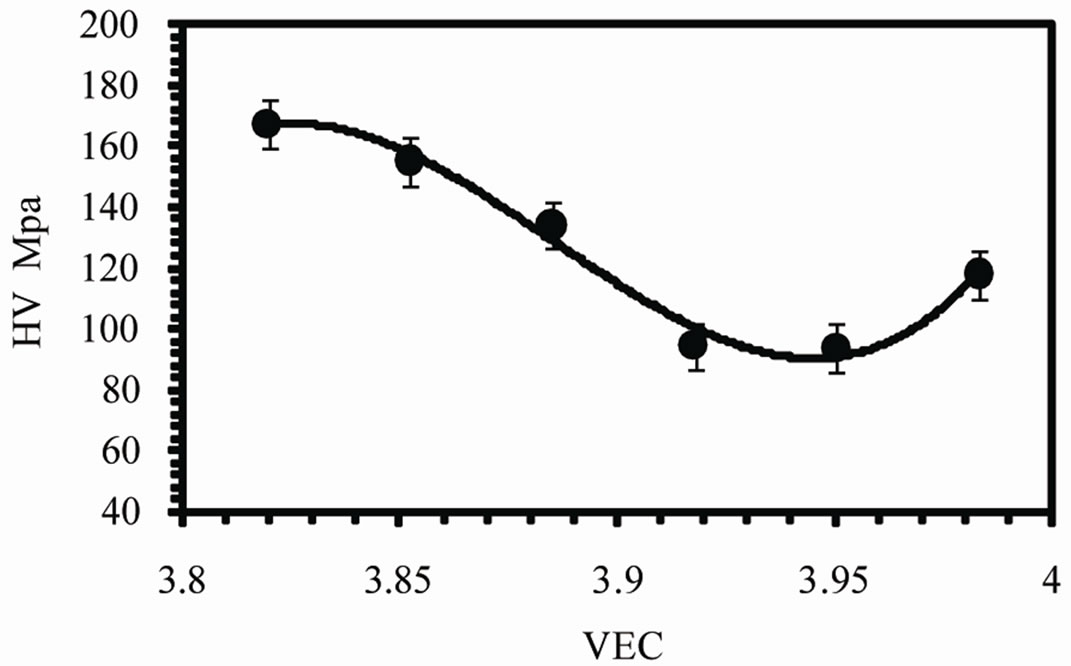 (c)
(c)
Figure 8. (a) Variation of Young’s modulus and (b) internal friction with axial ratio (c) Variation of Vickers microhardness number with VEC.
of Ag3Sn intermetallic compound which increases by increasing Ag concentration.
4. Conclusion
In this study the interaction between Fermi sphere and Brillouin zone and Hume-Rothery condition of phase stability have been verified. By increasing valence electron concentration VEC the diameter of Fermi sphere 2kF increases which leads to the increase in the diameter of Brillouin zone which arises from the decrease in volume of the unit cell. The electrical resistivity increases by increasing VEC due to the decrease in the relaxation time t with increasing VEC. Also it has been confirmed that the correlation between Young’s modulus and the axial ratio c/a of b-Sn unit cell. In conclusion, valence electron concentration is the most important factor for structure and properties changes of Sn-Ag alloys.
REFERENCES
- W. Hume-Rothery, “Research on the Nature, Properties and conditions of formation of Intermetallic Compounds, with Special Reference to Certain Compounds of tin,” Journal Institute of Metals, Vol. 35, 1926, pp. 295-299.
- G. V. Raynor and J. A. Lee, “The Tin-Rich Intermediate Phases in the alloys of tin with Cadmium, Indium and mercury,” Acta Metallurgica, Vol. 2, No. 4, 1954, pp. 616- 620. doi:10.1016/0001-6160(54)90197-2
- R. H. Kane, B. C. Giessen and N. J. Grant, “New Metastable Phases in Binary Tin Alloy Systems,” Acta Metallurgica, Vol. 14, No. 5, 1966, pp. 605-609. doi:10.1016/0001-6160(66)90068-X
- T. El-Ashram, “The relation between Valency, Axial Ratio, Young’s Modulus and resistivity of Rapidly Solidified Tin-Based Eutectic Alloys,” Journal of Materials Science: Materials in Electronics, Vol. 16, 2005, pp. 501- 505. doi:10.1007/s10854-005-2724-3
- K. Schubert, U. Roseler, W. Mahler, E. Doerre and W. Schuett, “Strukturuntersuchungen an einigen Valenzelektronen-armen Legierungen zwischen B-Metallen,” Z. Metallk, Vol. 45, 1954, pp. 643-647.
- A.-P. Tsai, “Decagonal structure of Al72Ni20Co8 studied by Atomic-Resolution Electron Microscopy,” Journal of Non-Crystalline Solids, Vol. 334-335, 2004, pp. 317-322. doi:10.1016/j.jnoncrysol.2003.11.038
- M. Kamal, A. B. El-Bediwi and T. El-Ashram, “The effect of Rapid Solidification on the Structure, Decomposition Behavior, Electrical and Mechanical Properties of the Sn-Cd Binary Alloys,” Journal of Materials Science: Materials in Electronics, Vol. 15, No. 4, 2004, pp. 211-217. doi:10.1023/B:JMSE.0000012457.77041.c6
- Y. A. Geller and A. G. Rakhshtadt, “Science of Materials,” Mir Publishers, Moscow, 1977.
- E. Schreiber, O. L. Anderson and N. Soga, “Elastic Constants, and Their Measurements,” McGraw-Hill Companies, Inc., New York, 1973.
- M. Hansen and K. Anderko, “Constitution of Binary Alloys,” 2nd edition, McGraw-Hill Companies, Inc., New York, 1958.
- T. El-Ashram, “Structure and properties of Rapidly Solidified Pure Tin,” Radiation Effects and Defects in Solids, Vol. 161, No. 3, 2006, pp.193-197. doi:10.1080/10420150500485192

