Materials Sciences and Applications
 Vol.3 No.1(2012), Article ID:16972,9 pages DOI:10.4236/msa.2012.31008

Synthesis and Piezoelectric Properties of Pb0.98Sm0.02[(Zry,Ti1–y)0.98(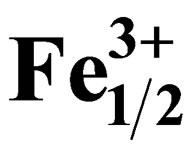,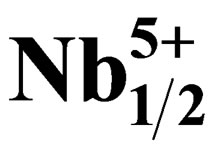80001449585 height=57.094998550415  />)0.02]O3 Ceramics

Fares Kahoul1,2*, Louanes Hamzioui1,2, Nora Abdessalem1, Ahmed Boutarfaia1,2

1Laboratoire de Chimie Appliquée, Université de Biskra, Biskra, Algérie; 2Département de Science de la Matière, Université de Ouargla, Ouargla, Algérie.

Email: {Fares_260, aboutarfaia}@yahoo.fr

Received July 9th, 2011; revised September 26th, 2011; accepted October 12th, 2011

Keywords: X-Ray Methods; Co-Existence of Phase; Piezoelectric Properties; Dielectric Properties

ABSTRACT

The structural and electrical properties of Pb0.98Sm0.02[(Zry,Ti1–y)0.98(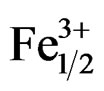,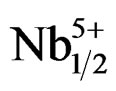)0.02]O3 ceramics system with the composition near the morphotropic phase boundary were investigated as a function of the Zr/Ti ratio by X-ray diffraction (XRD). Studies were performed on the samples prepared by solid state reaction for y = 0.47, 0.49, 051, 0.53, 0.55 and 0.57. Combined with piezoelectric properties results, it was consistently shown that an MPB exists between y = 0.51 and y = 0.55 in this system. When y < 0.51, the tetragonal phase dominates at ambient temperatures. In the range of y > 0.55, the rhombohedral phase dominates. Lattice parameters of the tetragonal phase and rhombohedral phase were found to vary with chemical composition. The average particle size ranged from 17.18 to 26.05 nm. The dielectric (ε = 1076), tanδ = 0.013 and piezoelectric properties (d31 = 122 pC/N, kp = 0.631 and Qm = 462) obtained were maximum at y = 0.55 which could be suitable for possible electromechanical and energy harvesting applications.

1. Introduction

Work carried out these last years on piezoelectric ceramics Pb(Zrx,Ti1–x)O3 attest the importance of these materials in the vicinity of the morphotropic phase boundary (MPB) where the two phases coexist and exhibit the highest values of the permittivity and the electromechanical coupling factor. This border separates the two ferroelectric phases, one is tetragonal, and the other is rhombohedral [1]. The PZT are often modified by the introduction of the doping agents into the sites A or/and in the sites B of perovskite ABO3 structure. The principal role of the doping agents is generally the improvement of the physical and mechanical properties of these materials. Substitutions in the crystal lattice called doping are often led with the aim to improve the specific properties of the PZT or sometimes adapt them to specific applications. These properties are generally improved by the additions of one or more cations which will replace Pb2+ in site A and/or couple (Zr4+/Ti4+) in site B of perovskite structure (ABO3) [2]. The work focuses, firstly, on the substitution of: Pb2+ with Sm3+, couple (Zr4+/Ti4+) with (Fe3+, Nb5+); and, secondly, on their effect on the piezoelectric properties of the solid solution:

Pb1–xSmx[(Zry,Ti1–y)0.98(Fe3+1/2,Nb5+1/2)0.02]O3.

Pb(Zrx,Ti1–x)O3 perovskite have been extensively studied with the objective to optimize their piezoelectric properties. The Zr/Ti ratio is known to strongly influence properties, such as the elastic constant, the permittivity, the coupling factor, etc. Near the morphotropic phase boundary (MPB), all these properties take extreme values when x corresponds to the composition of the morphotropic phase boundary (MPB) which separates the tetragonal (T) and rhombohedral (R) phases towards Tirich and Zr-rich sides, respectively [3,4]. Investigating the Pb(Zrx,Ti1–x)O3 system has shown the existence of an almost temperature-independent morphotropic phase boundary at x = 0.535, which separates a rhombohedral phase from a tetragonal one. By means of X-ray diffracttion, the co-existence of the two phases over a range of compositions around MPB was demonstrated [5-11].

The present work aims, first, to synthesize new materials which represent interesting electric and mechanical properties; and, second, to efficiently combine the dielectric and electromechanical properties of this system. The dielectric, ferroelectric, and the piezoelectric behaviors of the MPB system were examined and discussed.

2. Experimental Procedure

The specimens were manufactured by using a conventional mixed oxide process. The compositions used in this study were as follows:

Pb1–xSmx[(Zry,Ti1–y)0.98(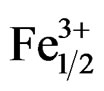,)0.02]O3 (hereafter named as PSZTFN). This study of this new system is carried out while varying y (47% ≤ y ≤ 57% with a step of y = 2%), by fixing x (x = 2%), and carrying out substitutions in site A and B of a perovskite structure by a mixture of the doping agents: acceptors and donors (Sm2O3, Fe2O3, Nb2O5). The starting materials were Pb3O4 (99.90%), ZrO2 (99.90%), TiO2 (99.90%), Fe2O3 (98%), Sm2O3 (99.90%) and Nb2O5 (99.6%).

Raw materials were mixed in acetone medium by using a magnetic stirrer during two hours. The obtained paste is being dried at 80˚C in a drying oven for two hours, and then crushed in a mortar out of glass during six hours. After crushing, the obtained powder is compacted in a form of pastilles with a pressure of 300 kg/cm2. Then, a preliminary calcination with 800˚C is carried out during two hours with a heating rate of 2 ˚C/mn. The calcined mixture is crushed for a second time during four hours, and then was quickly crushed in a form of pellets with a pressure of 1000 kg/cm2. These pellets are agglomerated at various temperatures of sintering (1100˚C, 1150˚C, 1180˚C, 1200˚C) during two hours. It is important to note that a lead loss is possible by evaporation of PbO which is very volatile in T ≥ 900˚C. To limit this effect; an atmosphere rich in PbO was maintained with the powder of PbZrO3 to the minimum to reduce this loss during sintering. The pastilles are metalized by using a thin layer of silver paste on the two faces.

X-ray diffraction (XRD, Siemens D500) was used to determine the crystalline phases present in the powder. The compositions of the PZT phases were identified by the analysis of the peaks [(002)T, (200)R, (200)T] in the 2θ range 43˚ - 46˚. The tetragonal (T), rhombohedral (R) and tetragonal-rhombohedral phases were characterized and their lattice parameters were calculated. The rhombohedral lattice parameter was calculated on the assumption that the rhombohedral distortion was constant (unit cell angle aR = 89.9˚) [6,7]. In order to ensure an accurate determination of the lattice parameters, the X-ray peaks were recorded gradually with 0.01˚ steps.

Electronic micrographs scanning (SEM) were taken from fractured as well as chemically etched surfaces. A section of the sintered sample was etched in a 5% HCl solution for 3 minutes. The fractured surfaces were used for grain size and morphology determination. The size distribution of the grains was measured and the results compared with each other. The size distribution of the pores and the total value of porosity were determined on a polished cross-section of the samples with an image analyzer.

The specimens were polished for the dielectric and piezoelectric studies. Silver paste was fired on both sides of the samples at 750˚C for forty five minutes as the electrodes for the dielectric and piezoelectric measurements. The dielectric response was measured at the frequency of 1 kHz by using an automatic LCR meter at a temperature ranging from 50˚C to 450˚C. Before measuring the piezoelectric properties, the specimens were poled in silicone oil at 110˚C by applying a d.c. field of 3.6 kV/mm for forty five minutes. Twenty four hours after poling, the piezoelectric properties: piezoelectric constant (d31), electromechanical planar coupling factor (kp) and mechanical quality factor (Qm) were measured by a method similar to that of the IRE standard. The resonance and anti-resonance frequencies were obtained by using the maximum and the minimum of spectra admittance.

3. Results and Discussion

3.1. Phase Analysis and Microstructure

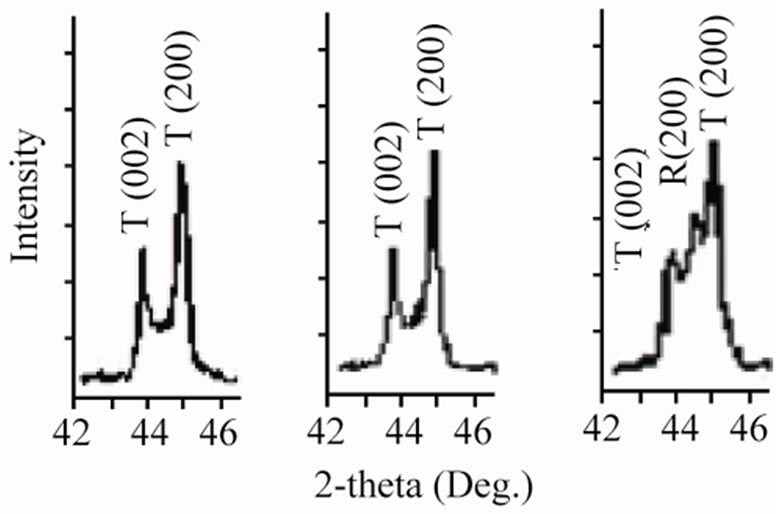
Sintered powders were examined by X-ray diffractometry to ensure phase purity, and to identify the crystal structure. It can be seen that all the samples show pure perovskite structure, suggesting that Sm, Fe and Nb diffuse into the PZT lattice to form a solid solution. Figure 1 shows the XRD patterns of (1–x)Pb (Zry,Ti1–y)O3-xSm (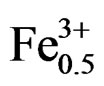,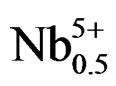)O3 ceramics sintered at 1180˚C for two

(a)(b)

Figure 1. X-ray diffraction patterns of (1–x)Pb (Zry,Ti1–y)O3 -xSm(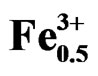,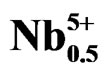)O3 ceramics sintered at 1180˚C for 2 h: (a) 47/53; (b) 49/51; (c) 51/49; (d) 53/47; (e) 55/45; (f) 57/43 The co-existence of tetragonal and rhombohedral splitting in the ((c), (d), (e)).

hours. It was found that the (1–x)Pb (Zry,Ti1–y)O3-xSm (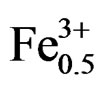,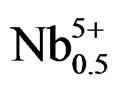)O3 ceramics formed the tetragonal structure in the case of y ≤ 0.51. The more the Zr/Ti ratio increases, the more the structure changes; and when the Zr/Ti was 0.51 ≤ y ≤ 0.55, morphotropic phase boundary (MPB), coexisting rhombohedral and tetragonal phases were observed.

At the sintering temperature of 1180˚C, we have studied the evolution of lattice parameters of the solution (1–x)Pb (Zry,Ti1–y)O3-xSm(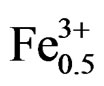,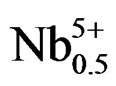)O3 as a function of the composition of y “Figure 2”. It is noted that these parameters are very sensitive to the variation of the composition of y, and the distortion of the perovskite structure cT/aT ratio decreases when the composition of y believes. The tetragonal phase shows that the parameter aT increases and cT decreases when the composition of y increases. The parameter aR of the rhombohedral phase increases with the increase in the composition of y. The influence of the substitution of Zr/Ti ratio on the structure of the parameters can be explained by the difference between the ionic rays of Zr and Ti (0.68 and 0.79 Å, respectively). This cannot provide a total homogeneity in the solid solutions containing both tetragonal and rhombohedral phases.

The variation in the lattice parameters of the identified phase composition shows that the values of the cT/aT ratio have decreased. This can be explained by microscopic compositional fluctuations occurring in these perovskite materials, which cannot provide a real homogeneity in the solid solutions that determine the co-existence of tetragonal-rhombohedral phases. The increase of the sintering temperature and the firing time enhanced the diffusion effects within these regions and led to a relative homogenization of the local composition in the material. The transition from tetragonal to rhombohedral phase as a function of composition can be visualized to occur as follows: 1) The tetragonal and rhombohedral distortions decrease continuously as one approaches the MPB composition from either side; 2) If the tetragonal to rhombohedral transition is first order, the two phases might coexist over some range of y around the MPB composition.

Figures 3(a)-(c) shows the SEM images of PSZTFN (47/53), PSZTFN (49/51) and PSZTFN (53/47) ceramics sintered at 1180˚C. All the sintered ceramics appear to be very dense and of a homogeneous granular structure. At first sight, the three compositions seem homogeneous and there do not seem to be grains of the pyrochlore phase which are identifiable by their pyramidal form. The ruptures with the grain boundaries are synonymous with a good sintering. It is noticed that the average diameter of the grains increases significantly with the increases in the Zr/Ti ratio. The intermediate size of the grains is 1,718 μm for the sample “Figure 3(a)” with Zr/Ti (47/53). For cons, the intermediate size of sample “Figure 3(b)” of the grains is larger (2,167 μm). In the case of ceramics “Figure 3(c)” with Zr/Ti (53/47), the intermediate size of the grains is larger than that of “Figure 3(a)” and “Figure 3(b)” (of the order 2,605 μm); and the broader the granulo-metric distribution “Figure 3(c)”, the more the size of the grains gets bigger [12]. The variation of the experimental density with Zr/Ti ratio in the PSZTFN ceramics system is shown in Figure 4. The density of the ceramics increases with the increase of Zr/Ti ratio. The observed increase in density is in agree-

Figure 2. Variation of: the unit cell dimensions and ratio cT/aT of PSZTFN as a function of composition (y).

(a)(b)(c)

Figure 3. Microstructure of Pb1-x Smx[(Zry,Ti1-y)0.98(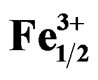,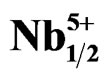)0.02]O3 ceramics sintered at 1180˚C for 2 h, (a) Zr/Ti = 47/53; (b) Zr/Ti = 49/51; (c) Zr/Ti = 53/47.

ment with the grain distribution observed in SEM microstructures.

3.2. Dielectric Properties

Figure 5 shows the variation of the dielectric constant as a function: of composition and of temperature at sintering temperatures 1100˚C, 1150˚C and 1180˚C. For the three temperatures of sintering 1100˚C, 1150˚C and 1180˚C, observed that the permittivity increases gradually with the increase in the composition of y and takes a maximum of 1076 for the sample with Zr/Ti = 55/45 included in the morphotropic phase boundary (MPB) at the temperature 1180˚C and then decreases. This maximum of dielectric activity can be explained by the presence of several directions of spontaneous polarization relating to the existence of the two structures rhombohedral and tetragonal.

Figure 6 is a plot of the dissipation factor (at room temperature, 1 kHz) versus composition of all samples sintered at various temperatures (1100˚C, 1150˚C, and 1180˚C). All the samples within the investigated compositional range (y = 0.47 - 0.57) have dissipation factors <3%.

The diffuse phase transition (DPT) is one of the distinguishing features for the relaxor ferroelectrics. Various models have been proposed for explaining the behavior of relaxor ferroelectrics e.g. the composition fluctuation model [13], the superparaelectric model [14], the dipolar glass model [15], and the random field model [16]. For PSZTFN type of relaxor ferroelectrics, the occurrence of the diffuse phase transition is due to the presence of 1:1 short-range non-stoichiometric ordering between Fe3+ and Nb5+ ions. The chemically ordered domains destroy the charge balance; however, the decrease of the free energy in the system caused by forming ordered domains is larger than the free energy increase by imbalance charge so that ordered domains could actually exist in spite of the inability to grow further because of the imbalanced charge. In the present work, Sm3+ ions substitute for Pb2+ ions on the A-site sublattice. Sm3+ is a very well-known donor dopant for the Pb2+ ions in the A-site sublattice in PZT systems and is reported earlier by other researchers [17,18]. Donor doping like Sm3+, could effectively compensate the imbalance charge resulting from ordering so that 1:1 short-range ordering regions grow larger. The growth increases the separation between disordered matrix. Thus the DPT behaviour can be consistently enhanced [19,20].

3.3. Piezoelectric Properties

The electromechanical variation of the coupling factor kp is very sensitive to the variation of the composition. The Zr/Ti ratio varies from 47/53 to 57/43. Figure 7 illustrates the electromechanical coupling factors (kp) of Pb1–x Smx[(Zry,Ti1–y)0.98(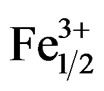,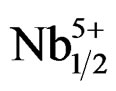)0.02]O3 sintered at 1180˚C. One notes an increase in the coupling factor kp along with an increase in the Zr rate until reaching a maximum value with Zr/Ti = 51/49 (kp = 0.632). On this side of Zr/Ti ratio value one also observed almost a stabilization

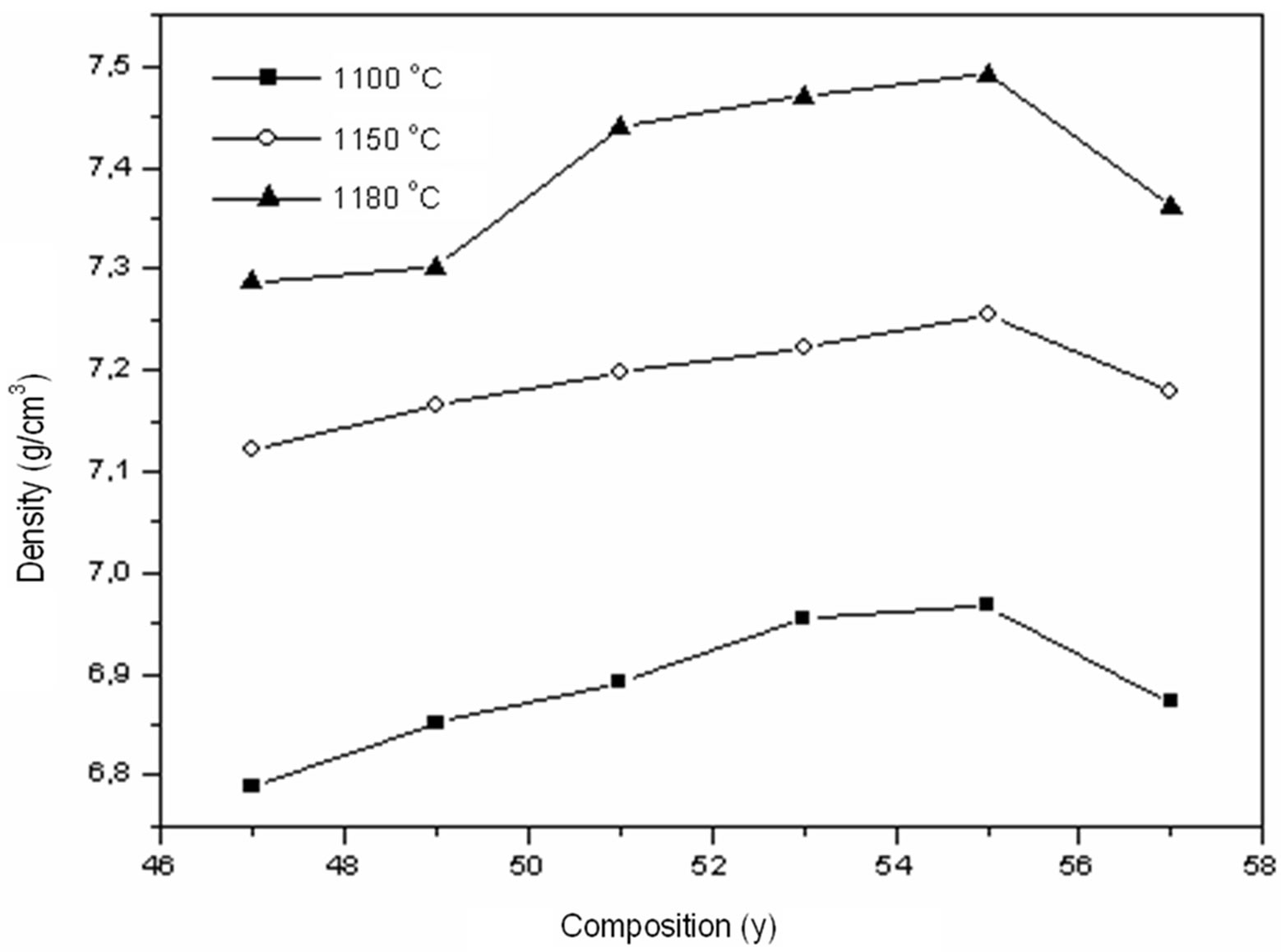
Figure 4. Density according to the variation of y (Zr) in the composition and sintering temperature.

of the electromechanical coupling factor kp, with Zr/Ti = 53/47 the value of kp = 0.63; and as for the sample with Zr/Ti = 55/45 the value of kp = 0.63. The kp value was also reported to have correlation with the specimen density. Thus, in addition to the low sinterability, high grain boundary density could also be observed in PSZTFN ceramics; and when Zr/Ti ratio increased, it might result in low kp value of the ceramics. Heywang [21] and Isupov [22] have explained this increase by the following opinion: during the polarization of material, the degree of domain alignment increases and becomes higher in the area of co-existence of the tetragonal and rhombohedral phases. This idea was underlined and confirmed by Dantsiger and Fesenko [23]. We can say that the zirconium rate for the compositions belonging to the morphotropic phase boundary (MPB), which combines two phases Tetragonal-Rhombohedral, lies between 51% and 55%.

The piezoelectric properties variation (d31 and Qm) with Zr/Ti ratio in the Pb1–xSmx[(Zry,Ti1–y)0.98(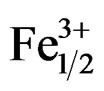,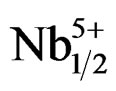)0.02]O3 ceramic system is depicted in Figure 8. The d31 and Qm of the ceramic system are enhanced with the increase of Zr/Ti ratio. It is observed in Figure 8 that as the Zr/Ti ratio increases, the value of d31 represents a peak of 122 at Zr/Ti ratio of 53/47; and when Zr/Ti ratio is further increased, the value of d31 decreases. Qm continues to increase, and finally it shows the maximum value when Zr/Ti ratio goes to 55/45 and then decreases. When the Pb1–xSmx[(Zry,Ti1–y)0.98(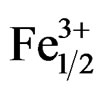,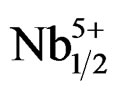)0.02]O3 system is doped with Sm3+, it replaces the Pb2+ ion at Asite; and Pb vacancies are created in the lattice to maintain the electroneutrality. In a lattice having Pb vacancies, transfer of atoms is easier than in a perfect lattice; and domain motion is easier. Such a mechanism is termed ferroelectrics softening. If the domain reorientation is enhanced, the ceramic will be easier to pole. If PZT is softened by donor doping, the coercive field will be lowered, the remnant polarization will be increased, the dielectric constant will be increased, and the piezoelectric properties will be enhanced [8,14].

The piezoelectric properties of PZT ceramics are influenced by the type and content of dopants. The dopant can improve the sintering process, produce ceramics with high specific mass, reduce the lead oxide evaporation, and prevent the formation of second phases [24]. Besides, dopants also engender the substitution of A or B cations of ABO3 perovskite structure. Ions of higher valence, such as Nb5+, cause vacancies in the A cation called lead vacancies; and the lower valence ions, as Fe3+, result in oxygen vacancies [25]. The additives that increase the amount of oxygen vacancies cause a small reduction of the unit cell dimensions, increase the internal stress; and, consequently, increase the coercitive field. Therefore, the additives that accept electrons are called hardener additives. The material doped with iron presents lower dielectric constant, and loses constant when the mechanic quality factor is increase [26]. Therefore, according to Takahashi [27] the vacancies of oxygen generated by the addition of iron are suppressed when there are niobium and iron equimolar compositions. In a polycrystalline system, dielectric and piezoelectric properties are dependent on both intrinsic and extrinsic mechanisms [28, 29]. Intrinsic contributions are from the relative ion or cation shift that protects the ferroelectric crystal structure. The extrinsic contributions are from the domain wall

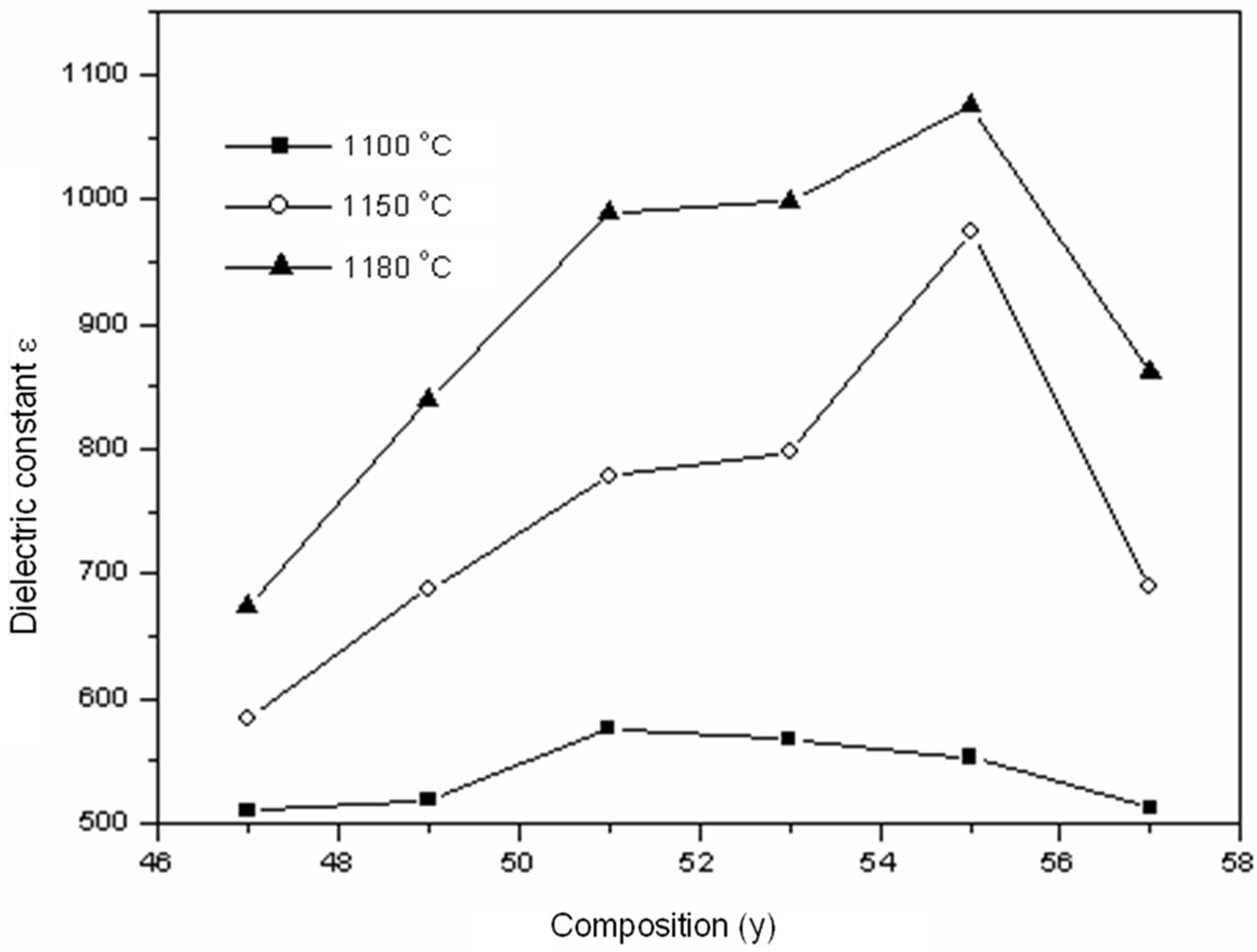
Figure 5. Dielectric constant (ε) according to the variation of y (Zr) in the composition and temperature.

motion. The extrinsic mechanisms are thermally activated processes, and can be frozen out at a very low temperature. The intrinsic mechanisms are due to the lack of MPB in the systems of Pb1–xSmx[(Zry,Ti1–y)0.98(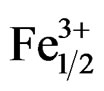,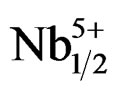)0.02]O3, and to the  increase of the BF content. Thus, the mechanical quality factor Qm increases with the increase of the ratio of Zr/Ti.

4. Conclusion

Investigations on the structure and properties of the Pb1–x Smx[(Zry,Ti1–y)0.98(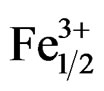,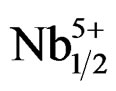)0.02]O3 system over the range y = 0.47 - 0.57 have revealed an MPB between y = 0.51 and 0.55, which separates a tetragonal phase from a rhombohedral phase. The effect of a sintering temperature on density and porosity was studied in order to reach the optimal sintering temperature. This temperature (1180˚C) corresponds to the maximum value of density; consequently, the minimum value of porosity corresponds to the product of better quality. The lattice parameters of the two structures tetragonal and rhombohedral vary with the variation of the Zr/Ti ratio in the matrix. The composition that contains Zr/Ti ratio of 55/45 gave the desirable piezoelectric properties, i.e. e = 2100, tanδ = 0.013, kp =

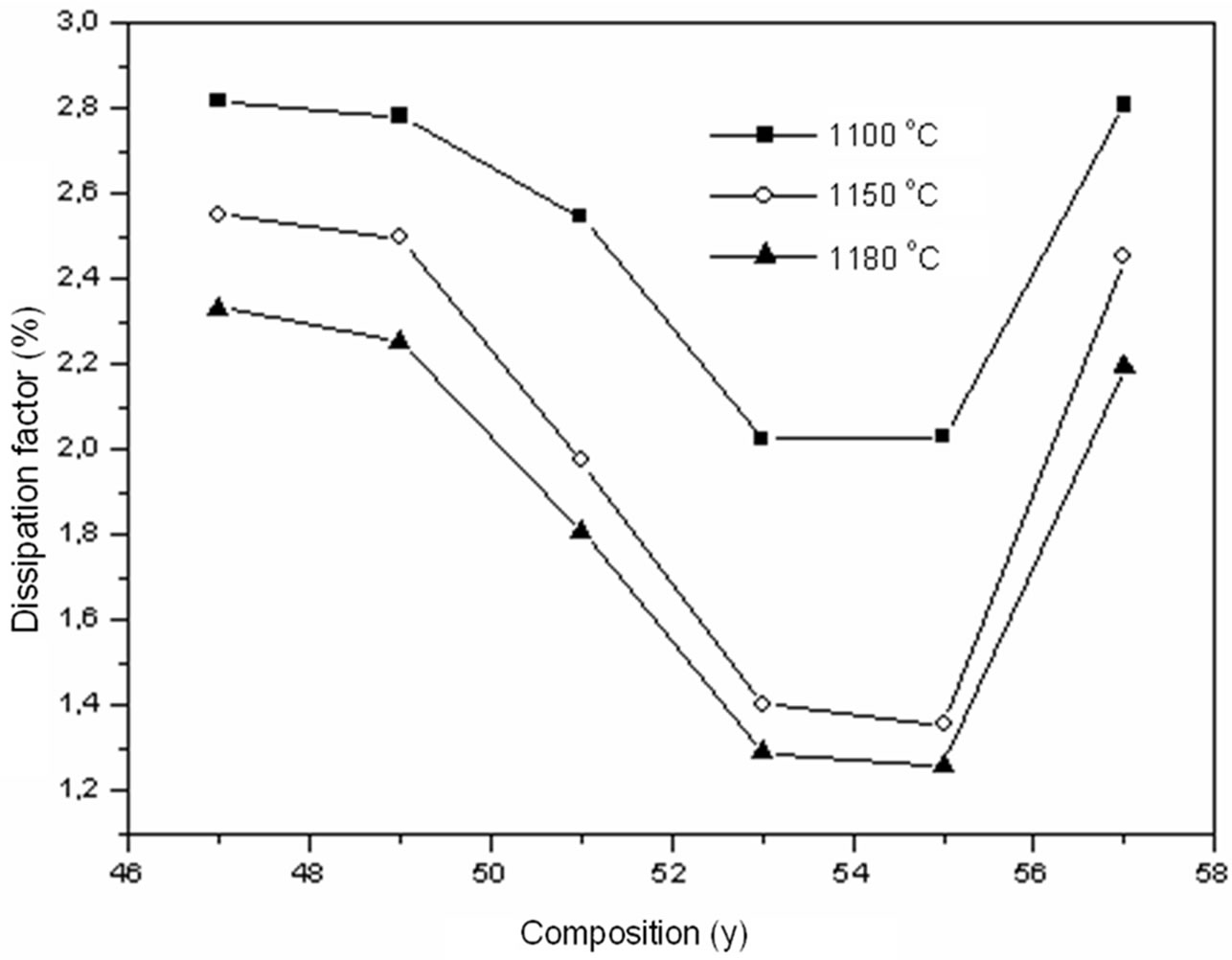
Figure 6. Dissipation factor according to the variation of y (Zr) in the composition and temperature.

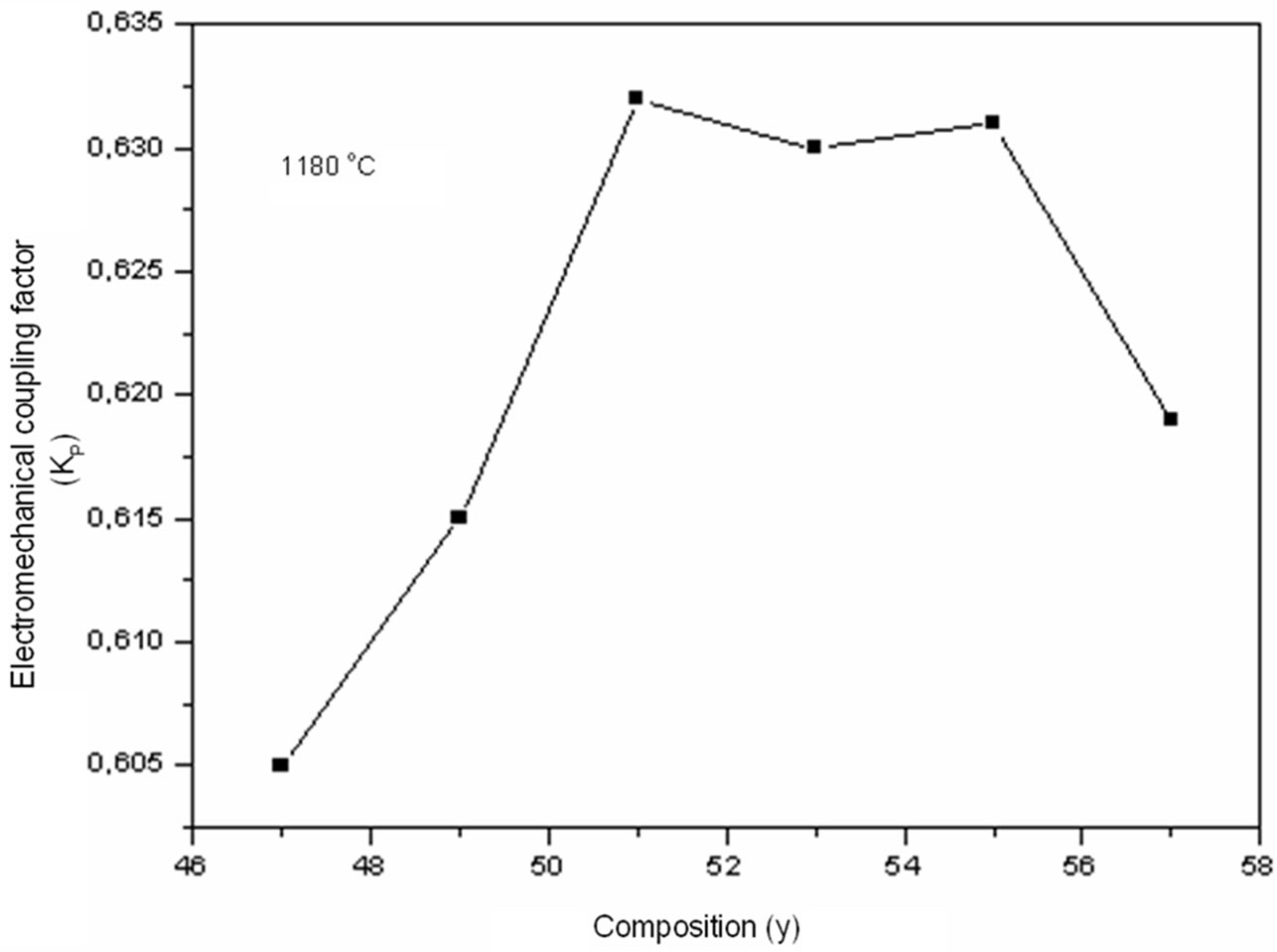
Figure 7. Electromechanical coupling factor (kp) according to the variation of y (Zr) in the composition.

Figure 8. Piezoelectric constant (d31) and mechanical quality factor (Qm) according to the variation of of y (Zr) in the composition.

0.63, Qm = 462 and d31 =122 pC/N, which makes this material a good candidate for high-power multilayer piezoelectric transformer applications.

REFERENCES

  1. B. V. Hiremath, A. I. Kingon and J. V. Biggers, “Reaction Sequence in the Formation of Lead Zirconate-Lead Titanate Solid Solutions: Role of Raw Materials,” Journal American Ceramic Society, Vol. 66, No. 11, 1983, pp. 790-793. doi:10.1111/j.1151-2916.1983.tb10564.x
  2. S. S. Chandratreya, R. M. Fulrath and J. A. Y. Pask, “Reaction Mechanisms in the Formation of PZT Solid Solutions,” Journal American Ceramic Society, Vol. 64, No. 7, 1981, pp. 422-425. doi:10.1111/j.1151-2916.1981.tb09883.x
  3. A. Boutarfaia, “Study of the Solid State Reaction and the Morphotropic Phase Boundary in Pb(Zr, Ti)O3-Pb(Fe1/5, Ni1/5, Sb3/5)O3 Ceramics,” Ceramics International, Vol. 27, No. 1, 2001, pp. 91-97. doi:10.1016/S0272-8842(00)00047-X
  4. N. Abdessalem and A. Boutarfaia, “Effect of Composition on the Electromechanical Properties of Pb[ZrxTi(0.9-x)- (Cr1/5, Zn1/5, Sb3/5)0.1]O3 Ceramics,” Ceramics International, Vol. 33, No. 2, 2007, pp. 293-296. doi:10.1016/j.ceramint.2005.08.008
  5. K. Kakegawa, J. Mohri, T. Takahashi, H. Yamamura and S. Shirasaki, “A Compositional Fluctuation and Properties of Pb(Zr, Ti)O3,” Solid State Communications, Vol. 24, No. 11, 1977, pp. 769-772. doi:10.1016/0038-1098(77)91186-3
  6. P. Ari-Gur and L. Benguigui, “X-Ray Study of the PZT Solid Solutions near the Morphotropic Phase Transition,” Solid State Communications, Vol. 15, No. 06, 1974, pp. 1077-1079. doi:10.1016/0038-1098(74)90535-3
  7. A. Boutarfaia and S. E. Bouaoud, “Tetragonal and Rhombohedral Phase Co-Existence in the System: PbZrO3- PbTiO3-Pb(Fe1/5, Ni1/5,Sb3/5)O3,” Ceramics International, Vol. 22, No. 4, 1996, pp. 281-286. doi:10.1016/0272-8842(95)00102-6
  8. P. Ari-Gur and L. Benguigui, “Direct Determination of the Coexistence Region in the Solid Solutions Pb(Zrx- Ti1-x)O3,” Journal of Physics D: Applied Physics, Vol. 8, No. 15, 1975, pp. 1856-1862. doi:10.1088/0022-3727/8/15/018
  9. A. Boutarfaia, C. Boudaren, A. Mousser and S. E. Bouaoud, “Study of Phase Transition Line of PZT Ceramics by X-Ray Diffraction,” Ceramics International, Vol. 21, No. 6, 1995, pp. 391-394. doi:10.1016/0272-8842(95)94463-K
  10. R. B. Atkin and R. M. Fulrath, “Point Defects and Sintering of Lead Zirconate-Titanate,” Journal American Ceramic Society, Vol. 54, No. 5, 1971, pp. 265-270. doi:10.1111/j.1151-2916.1971.tb12286.x
  11. A. Boutarfaia, “Investigations of Co-Existence Region in Lead Zirconate-Titanate Solid Solutions: X-Ray Diffraction Studies,” Ceramics International, Vol. 26, No. 6, 2000, pp. 583-587. doi:10.1016/S0272-8842(99)00099-1
  12. O. Ohtaka, R. Von Der Mühll and J. Ravez, “Low-Temperature Sintering of Pb(Zr,Ti)O3 Ceramics with the Aid of Oxyfluoride Additive: X-Ray Diffraction and Dielectric Studies,” Journal American Ceramic Society, Vol. 78, No. 3, 1995, pp. 805-808. doi:10.1111/j.1151-2916.1995.tb08251.x
  13. G. A. Smolenskii and A. I. Agranovskaya, “Dielectric Polarization of a Number of Complex Compounds,” Soviet Physics Solid State, Vol. 1, 1960, pp. 1429-1437.
  14. L. E. Cross, “Relaxor Ferroelectrics,” Ferroelectrics, Vol. 76, No. 3-4, 1987, pp. 241-267. doi:10.1080/00150198708016945
  15. D. Viehland, J. F. Li, S. J. Jung and L. E. Cross, “Dipolar-Glass Model for Lead Magnesium Niobate,” Physical Review B, Vol. 43, No. 10, 1991, pp. 8316-8320. doi:10.1103/PhysRevB.43.8316
  16. R. Fisch, “Random-Field Models for Relaxor Ferroelectric Behavior,” Physical Review B, Vol. 67, No. 9, 2003, pp. 4110-4117. doi:10.1103/PhysRevB.67.094110
  17. H. Xu, “Ferroelectrics and Piezoelectric Materials,” Science Press, Beijing, 1978.
  18. G. H. Haertling, “Ferroelectric Ceramics: History and Technology,” Journal American Ceramic Society, Vol. 82, No. 4, 1999, pp. 797-818. doi:10.1111/j.1151-2916.1999.tb01840.x
  19. W. Z. Zhu, A. Kholkin, P. Q. Mantas and J. L. Baptista, “Dielectric Response of PZN-Based MPB Composition Doped with Lanthanum,” Materials Chemistry and Physics, Vol. 73, No. 1, 2002, pp. 62-69. doi:10.1016/S0254-0584(01)00356-X
  20. K. M. Lee, H. M. Jang and W. J. Park, “Mechanism of 1:1 Nonstoichio-Metric Short-Range Ordering in La-Doped Pb(Mg1/3Nb2/3)O3 Relaxor Ferroelectrics,” Journal of Materials Research, Vol. 12, No. 6, 1997, pp. 1603-1613. doi:10.1557/JMR.1997.0220
  21. W. Heywang, “Ferroelektrizität in Perowskitischen Systemen und Ihre Technischen Anwendungen,” Zeitschrif Angewandte Physik, Vol. 19, 1965, pp. 473-481.
  22. V. A. Isupov, “X-Ray Study of the PZT Solid Solutions near the Morphotropic Phase Transition,” Solid State Communications, Vol. 17, No. 11, 1975, pp. 1331-1333. doi:10.1016/0038-1098(75)90595-5
  23. A. Y. Dantsiger and E. G. Fesenko, “Relation between the Main Electro-Physical and Structural Parameters of Ferro- (Piezo-) Electric Ceramics and Methods of Their Changing,” Journal of the Physical Society of Japan, Vol. 28, 1970, pp. 325-327.
  24. C. Miclea, C. Tanasoiu, C. F. Miclea, L. Amarande, A. Gheorghiu and F. N. Sima, “Effect of Iron and Nickel Substitution on the Piezoelectric Properties of PZT Type Ceramics,” Journal of the European Ceramic Society, Vol. 25, No. 12, 2005, pp. 2397-2400.
  25. J. E. Garcia, R. Pérez, A. Albareda and J. A. Eiras, “Non-Linear Dielectric and Piezoelectric Response in Undoped and Nb5+ or Fe3+ Doped PZT Ceramic System,” Journal of the European Ceramic Society, Vol. 27, No. 13-15, 2007, pp. 4029-4032. doi:10.1016/j.jeurceramsoc.2007.02.086
  26. Z. Yang, R. Zhang, L. Yang and Y. Chang, “Effects of Cr2O3 Doping on the Electrical Properties and the Temperature Stabilities of PNW-PMN-PZT Ceramics,” Materials Research Bulletin, Vol. 42, No. 12, 2007, pp. 2156- 2162.
  27. S. Takahashi, “Effects of Impurity Doping in Lead Zirconate-Titanate Ceramics,” Ferroelectrics, Vol. 41, No. 1, 1982, pp. 143-156. doi:10.1080/00150198208210617
  28. C. A. Randall, N. Kim, J. P. Kucera, W. Cao and T. R. Shrout, “Intrinsic and Extrinsic Size Effects in FineGrained Morphotropic-Phase-Boundary Lead Zirconate Titanate Ceramics,” Journal American Ceramic Society, Vol. 81, No. 3, 1998, pp. 677-688. doi:10.1111/j.1151-2916.1998.tb02389.x
  29. Q. M. Zhang, H. Wang, N. Kim and L. E. Cross, “Direct Evaluation of Domain-Wall and Intrinsic Contributions to the Dielectric and Piezoelectric Response and Their Temperature Dependence on Lead Zirconate-Titanate Ceramics,” Journal of Applied Physics, Vol. 75, No. 1, 1994, pp. 454-459. doi:10.1063/1.355874

NOTES

*Corresponding author.

Journal Menu >>