ABSTRACT

In this treatise we stress the analogy between strongly interacting many-body systems and elementary particle physics in the context of Quantum Field Theory (QFT). The common denominator between these two branches of theoretical physics is the Green’s function or propagator, which is the key for solving specific problems. Here we are concentrating on the vacuum, its excitations and its interaction with electron and photon fields.

Keywords:

Quantum Vacuum, Quantum Electrodynamics, Quantum Field Theory, Relativistic Quantum Mechanics, Feynman Diagrams

1. Introduction

It is the aim of this treatise to pay tribute to Feynman’s propagator method and its visualization in Feynman diagrams. This method has applications as wide as e.g. many electron theories, condensed matter physics and quantum field theory.

It consists on one hand of showing for intricate mathematical expressions of the underlying physics, and on the other hand, of applying pre-established rules to these graphs, to set up these expressions.

Here we are not giving a lecture on these procedures; we are merely applying them to vacuum excitations interacting with electron and photon fields.

Starting from routinely used techniques as e.g. developed in the book by M. E. Peskin and D. V. Schroeder [1] , we introduce some novelties in the derivation of final results. In particular, a discussion of the electron self-energy result in terms of a Zitterbewegung is presented.

In a first introductory part, we recall the basic facts of the second quantization of the Klein-Gordon and the Dirac field and discuss the resulting consequences.

Then we define propagators for the Dirac and photon fields and use them to treat interactions of these fields with the vacuum. More specifically we study the electron and photon self-energies.

We do not concern ourselves in general with collisions between elementary particles, although this is one of the main subjects met in Quantum Field Theory. As an exception we consider however electron-electron scattering because of its connection with vacuum polarization. The resulting physical facts are discussed extensively.

2. Particles and Fields

It is the aim of this section to recall how, in relativistic quantum physics, negative energy states are avoided by adopting the field viewpoint. For this purpose we chose as the simplest possible case that of an uncharged particle obeying the Klein-Gordon equation. The essential arguments developed here then apply equally to the case of more general systems.

Negative energy states, causality.

In quantum mechanics we associate a particle with a wave function 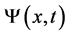depending on time and space coordinates and respectively. The wave functions are solutions of a differential equation known as the Schrödinger equation. In a heuristic way this equation can be derived by replacing the energy and momentum of the particle by operators, according to the relations

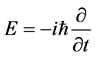and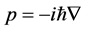

For a particle we then have in the non relativistic case 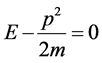yielding

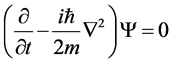(2.1)

In the relativistic case we start from the relation 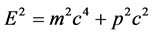and obtain, after inserting the relevant differential operators

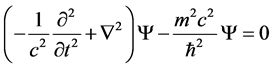(2.2)

This relativistic version of the Schrödinger equation is called the Klein-Gordon equation. It is important to note that in contrast to the non relativistic Equation (2.1) the Klein-Gordon equation contains the second time derivative meaning that it allows for negative energy solutions. Using from now on natural units, , 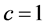we write explicitly

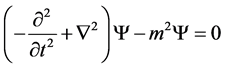(2.3)

Setting

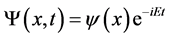
Equation (2.3) reduces to

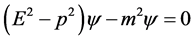(2.4)

where we have used.

For plane wave solutions with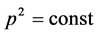, we then have the energy relations

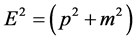(2.5a)

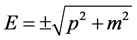(2.5b)

Hence there are negative energy solutions. The question arises whether these solutions cannot be discarded as non physical. But in that case we would not have a complete set of basic functions since these solutions are part of it. In actual calculations this could yield erroneous results. Furthermore, in a less obvious way, omitting these solutions leads to a violation of the principle of causality as we shall demonstrate now.

Consider the amplitude for the evolution of a free particle from an initial to a final position during the time interval. Discarding negative energy states this amplitude would be

(2.6)

Inserting the wave functions

(2.7)

we have

(2.8)

Using polar coordinates as follows:

;

we arrive after integration over at the expression

(2.9)

For simplicity we set. With a convergence factor

inserted the value of this integral is known [2] . Setting

its value is proportional to the Bessel function

up to a rational function of and. For large values of its argument the

Bessel function reduces essentially to the exponential [3] , leading

for to the result

(2.10)

Given this factor in the expression of we have a non-zero amplitude outside the light cone, thus violating the principle according to which space like separated events cannot be causally connected. Consequently violation of the causality principle occurs if only positive energy functions are taken into account.

There are however other shortcomings contained in the relativistic particle theory. One could argue that any positive energy state must be unstable since after some time the particle would fall into a lower energy state, in the same way as an atomic electron in an excited state falls into the ground state after some short lifetime. In the case of fermions this can be prevented by assuming, following Dirac, that all negative energy states are occupied already. This situation is due to the fact that, according to the Pauli principle, each state can only receive one electron. The completely filled negative states constitute the Dirac sea. Moreover, this picture has led Dirac to the prediction of the positron, i.e. a positively charged electron, appearing as a hole in the Dirac sea when by some process an electron is removed from it.

It is however possible to give a less artificial description of relativistic quantum particles by adopting the field viewpoint which will be presented now.

Lagrangian field method

We consider a field function depending on the time-space vector with components. Distinguishing between contra- and covariant components, respectively, we further have and a similar

relation with the metric tensor As usual, Greek

indices belong to the Minkowski four-space, Latin ones to ordinary space, with.

In analogy with classical mechanics, we introduce a Lagrange function, having here the character of a density, given by the expression, where we have set

.

Note also the complementary relation. We now define an

action integral over a region bordered by a closed surface, as follows:

(2.11)

Varying this integral in the usual way according to the relation

(2.12)

and using the identities

we arrive at

(2.13)

The last term in the parenthesis can be seen as the four-divergence of a four-vector proportional to. Therefore with Gauss’s theorem it can be transformed into a surface integral over the border. Since the Lagrange method postulates at the surface, this term disappears. On the other hand, if the action integral has to be an extremum, must vanish for any value of. This leads to the familiar Euler-Lagrange equations

(2.14)

or more explicitly

. (2.15)

These equations apply to classical fields, e.g. one component of the electromagnetic vector potential, as well as to wave functions in particle quantum mechanics.

As an example let us therefore consider the Klein-Gordon wave function.

Setting

(2.16)

we write and hence

yielding with the Klein-Gordon equation

(2.17)

The Hamiltonian.

In order to establish a link with classical mechanics, we first conceive the space coordinates as a countable set, each element occupying an infinitesimal space segment.

Considering the classical expression of the Hamiltonian

(2.18)

with the canonical variable obeying the relation

(2.19)

we have the correspondence

defining the canonical variable

. (2.20)

With these definitions we obtain for the classical relation (2.18) the following equivalent expression:

(2.21)

Switching now to the limit of continuous space coordinates, this result takes the form

(2.22)

where represents the Hamiltonian density

(2.23)

with the canonical momentum given by

. (2.24)

Let us consider as an example the Klein-Gordon case.

According to Equation (2.16) the Lagrange density can be written as

. (2.25)

We then have and hence

. (2.26)

Second quantization.

Simply speaking, a given wave function is quantized if it is replaced by an operator. This is familiar in quantum electrodynamics where e.g. one component of the vector potential is replaced by photon creation and annihilation operators. A similar procedure can be applied to quantum mechanical wave functions and in this latter case one then talks of second quantization, since the wave functions are already obtained by a first quantization procedure. Note however that the term second quantization is not universally accepted.

Here we consider again as an example the Klein-Gordon case, which constitutes the simplest one, as it concerns spinless particles like K or π mesons.

Let us first switch from space to space by introducing the following transformations:

. (2.27a)

(2.27b)

(2.27c)

The Hamiltonian density then takes the form

(2.28)

Since we want to quantize the system by replacing wave functions with operators in the Schrödinger picture, we disregard in this expression.

Integrating over the space coordinates, we thus arrive at the following expression for the Hamiltonian in terms of functions in space:

(2.29)

with

(2.30)

To obtain Equation (2.29) we have made use of the relation

The parenthesis inside the integral of Equation (2.29) reminds one of the Hamiltonian

of a harmonic oscillator.

In the latter case quantization is achieved by introducing creation and destruction operators, , according to the relation

with the commutator.

We therefore try in Equation (2.29) the substitutions

(2.31a)

(2.31b)

The parenthesis inside the integral in Equation (2.29) is then found to be given by the expression

Since complete summation over takes place, we can disregard the minus signs of the indices and write

We thus obtain for the Hamiltonian the following result

(2.32)

According to general rules of quantum physics, the commutation relation for canonical variables takes the following form in the present case:

. (2.33)

Inserting into the commutator the transformation relations given By equation’s (2.27a), (2.27c) we write

(2.34)

Substituting for the expressions given by Equation’s (2.31a), (2.31b) we obtain after a lengthy but straightforward calculation

(2.35)

Adopting the trial rule

(2.36)

Equation (2.35) reduces to

(2.37)

Substituting this result into Equation (2.34) we recover the commutation relation of Equation (2.33). This confirms the validity of the trial rule of Equation (2.36).

In the field equations developed above the number of particles concerned is not specified. Let us now be more specific by introducing single particle states assumed to constitute an orthonormal set in a given inertial frame. Acting with the Hamiltonian of Equation (2.32) on one of these states, e.g., and using Equation (2.36) for the commutator, we obtain the formal expression

(2.38)

The second term on the r.h.s. of this equation contains the infinite quantity and moreover it involves an infinite sum over energies. Mostly this term can be considered as some sort of ground state energy which cannot be detected experimentally and thus can be ignored.

In order to establish the time dependence of the operators and one has to replace them by Heisenberg operators according to the relation

and similarly for.

Starting from the expressions (2.31a), (2.31b) we evaluate the corresponding Heisenberg operators of and as follows:

Acting on an eigenstate of, according to Equation (2.38), the infinite zero-point energy term cancels in the operator product since it is a c number. We are thus left with the expression

using

.

Similarly we have

Hence the requested operator equations are

(2.39a)

(2.39b)

With Equation (2.31b) the quantized form of Equation (2.27a) becomes

(2.40)

where Equation’s (2.39a), (2.39b) have been used.

Introducing the Lorentz invariant scalar product in four space, with and, we obtain for the quantized field the expression

. (2.41)

Causality again.

As mentioned earlier, two points with space like separation

are not causally connected. This means that in this case, which corresponds to the region outside the light cone, the commutator must vanish.

Starting from Equation (2.41) the commutator is given by the expression

(2.42)

where the operator commutation rule of Equation (2.36) has been used. In order to obtain zero for this quantity, the inversion transformation has to be applied to the second integral. However, this is only legitimate if this transformation leaves the value of the integral invariant. This we shall discuss now. First set, with,. Then we have

(2.43)

Now we define a space like surface [3]

(2.44)

Without loss of generality we can restrict ourselves to the plane where the surface of Equation (2.44) appears as the curve

see Figure 1 (2.45)

Now take a particular point on this curve and rotate the coordinate frame in both terms of Equation (2.42) from to.

One then has the relations

(2.46)

Hence the transformed quantities are

yielding the following result in terms of rotated quantities:

Now the cumbersome factor has disappeared and the transformation leaves the value of the second integral unchanged, since in this integral one can change the sign of the integration variable without affecting its value. The fact that for any point on a given curve the corresponding coordinate rotation can be made, and that this is true for any curve, proves the statement that the commutator vanishes at any point outside the light cone.

Inside the light cone, i.e. for time like separations, the commutator does not vanish so that in this region points can be causally connected. It is however interesting to note that the corresponding commutator is invariant with respect to proper Lorentz transformations as shown e.g. in ref. [1] .

Note finally, that in many calculations the infinite energy of the vacuum state is eliminated by performing normal ordering of operators. It consists in reshuffling operator products in such a way that destruction operators always stand on the right of creation operators.

Generalizations [4] [5] [6] .

Particles obeying the Klein-Gordon equation do not bear any electric charges. In order to treat charged particles, complex wave functions have to be introduced into the theory. Even more profound modifications are necessary in the case of electrons according to the Dirac theory. Here, due to the presence of spin, wave functions are represented by spinors consisting of four functions as components of a vector. An even more striking difference occurs if second quantization is performed. In this case, the fermion character of the particle is taken into account in postulating anti-commutation rules for the field operators instead of the commutation rules pertaining to bosons.

However, the general idea of avoiding negative energy states by means of second quantization, already applied to the Klein-Gordon case, remains essentially the same in this and other situations.

3. Symmetry Transformation Relations

An essential feature of relativistic particles and fields is their behaviour with respect to transformations of the Lorentz group.

Transformation operators

We recall that the elements of this group are three rotations in the xy, xz, and yz planes around the z, y and x axis respectively, completed by three pseudo-rotations belonging to the xt, yt and zt planes respectively. These transformations can be viewed as an infinite succession of infinitesimally small rotations which generate a representation of the group. Designating the rotation operator with respect to the plane as, and the corresponding rotation parameter as, then an infinitesimal transformation is generated by the operator

(3.1)

yielding for the finite Lorentz transformation operator the expression

. (3.2)

Recalling that the familiar expression for rotations in ordinary space can be generalized to Minkowski space as

, (3.3)

we can generate a four dimensional representation of the proper Lorentz group by acting with this operator on the vector. Using the relations

, (3.4)

we consider the example, all other equal zero. Equation (3.1) then yields the matrix

(3.5)

This matrix thus corresponds to a rotation by an infinitesimal angle in the plane as can be shown by multiplying the matrix by the vector.

As a second example we consider the Lorentz boost in the direction by setting with all others equal zero. Then the relation

(3.6)

with substituted into Equation (3.1) leads to the result

(3.7)

Note that the factor in Equation (3.1) disappears because in both examples two equal terms are accounted for. Note also that by multiplying the matrices

of Equation’s (3.5) and (3.7) by the column vector one recovers the usual

relations for the corresponding infinitesimal rotations and Lorentz boosts.

Applying a Lorentz transformation as expressed by the operator of Equation (3.2) to wave functions, one obtains the following change:

(3.8)

The criterion for the corresponding wave equations to be valid is their Lorentz invariance. This property can be established by proving that the Lagrange density, from which a given wave equation is derived, is a Lorentz scalar. We shall now demonstrate this point in the particular case of the Klein-Gordon equation.

We cast the Lagrange density of Equation (2.16) in the form

(3.9)

with only one type of differential operator. With the transformation of Equation (3.8), i.e.

(3.10)

the scalar property of is obvious. We therefore focus on the quantity and write

(3.11)

where we have omitted on the r.h.s. the argument of the functions. Note also that the horizontal shift of the lower indices on matrix elements allows us to distinguish between line and column indices. Since matrix elements are c-numbers, their product can be treated separately. It is sufficient to do this in the limit of infinitesimal rotations. The more abstract general treatment can be found in the literature e.g. in ref. [1] .

According to Equation’s (3.1) and (3.2) we write

(3.12)

With the defining relation

(3.13)

Treating only the change introduced by the transformation and given the fact that is an infinitesimal quantity, we consider the expression

(3.14)

In the first term the indices and are eliminated yielding with,

no summation

whereas for the second term we find with, ,

no summation

Hence the final result

no summation (3.15)

Suppose now that and belong both to ordinary space i.e.

then the elements are both equal to, but as shown by Equation (3.5), we have and the sum in Equation (3.15) is zero. In the opposite case of Lorentz boosts with e.g., we have and whereas, according to Equation (3.7) and the sum is again zero. This proves the statement that Lorentz transformations do not affect the Lagrangian density function, except for the argument of the wave functions, and hence it is a Lorentz scalar. The resulting Euler-Lagrange equation, i.e. the wave function, has therefore a Lorentz invariant form.

The proof given here for infinitesimal variations is generally valid, since finite transformations involve an infinite succession of infinitesimal ones. As already mentioned, more formal proofs are found in the literature, but we thought it instructive to approach the problem by explicit calculations as well.

Spinors.

Having treated as an example the case of a structure less particle obeying the Klein-Gordon equation, we are now moving to the case of the electron, where in addition to space coordinates spin variables have to be considered, together with the existence of an electric charge.

Introducing spin functions, with the + − signs indicating spin variables, in a given frame, the wave function in four space can be written in the form

(3.16)

Considering components etc. as elements of a vector in spin space, we can also write

(3.17)

where the functions etc depend on both the space and the spin variable. The column vector of Equation (3.17) is known as a spinor.

Its Lorentz transformation can be expressed as follows:

(3.18)

where it is understood that the operator acts only on spin states.

We now define operator matrix elements by introducing for the limiting expression

(3.19)

with being the usual rotation and boost parameters.

We now recall that spin functions transform under rotations in ordinary space according to the Pauli spin matrices with

(3.20)

Then clearly, ordinary space rotations occur according to the relation

(3.21)

i j k in normal order.

Remark: normal order means that i j k are all different and that starting with 1 2 3 an odd number of permutations introduces a minus sign. One may ensure this property automatically by multiplying with a quantity known as the -tensor.

The question now arises, what happens in the case of Lorentz boosts? Without entering into details, we only state the answer given by Dirac’s theory according to the relation

(3.22)

Hence the matrices of Equation’s (3.21) and (3.22) constitute a four-dimen- sional representation of the Lorentz group known as the Dirac-Pauli representation.

The Weyl representation.

The Dirac-Pauli representation is reducible since its matrices can be brought into diagonal form by a unitary transformation involving the matrices

(3.23)

With these matrices we have

and hence

(3.24)

whereas the matrices remain unaffected.

Designating as left and right handed spinors and the spinors which now replace and, we have instead of Equation’s (3.21), (3.22) the relations

and (3.25)

Taking as an example the values, with particular figures for and all other equal 0, Equation’s (3.19) and (3.25) then yield the equation

, (3.26)

showing that the functions and, called Weyl spinors, transform independently from each other.

Clearly, these relations can be generalized for arbitrary rotation and boost parameters described by vectors and respectively. This leads to the transformation relations

(3.27a)

(3.27b)

Hence the Weyl spinors, constitute the basis for two-dimensional representations of the Lorentz group, instead of the reducible four-dimensional representation of the Dirac-Pauli basis.

In order to explain the designations of as left and right handed spinors, we consider the fact that they are eigenstates of the helicity operator

with eigenvalues for left and for right handed

spinors.

As an example the spinors introduced in Section 4 are right handed for those of Equation’s (4.13a), (4.15a) and left handed for those of Equation’s (4.13b), (4.15b). This can be shown by applying the helicity operator with to these spinors.

Connection with wave equations.

The wave equation for spinors is Dirac’s equation, which can be derived from the Lagrange density

(3.28)

as the corresponding Euler-Lagrange equation applied to, with the result

. (3.29)

Note that for and similar products Feynman has introduced the slash notation.

The matrices entering the Lagrange density are of vital importance, since in choosing them in an appropriate way, one meets the condition that has to be a Lorentz scalar, necessary for the corresponding wave function to be valid. As a consequence, there is clearly a connection between these matrices and the Lorentz transformation properties of the spinors. The corresponding relations are derived in many textbooks and will be given here only in their final form. According to Dirac, the following equations hold:

(3.30)

(3.31)

where the + index indicates an anticommutator. Note that later in this text the anticommutator will be designated by the symbol.

Given the fact that the matrices are different in the Dirac and the Weyl representation, one would expect a similar difference in the matrices. Substituting in Equation’s (3.30), (3.31) the special values, , one obtains

and (3.32)

Making the guess that is equal in both the Dirac and the Weyl representation, i.e. for

Dirac and Weyl

one obtains the result

(3.33)

By setting

Dirac (3.34)

Weyl (3.35)

one then obtains the following relations:

The Dirac equation, given in its general form by Equation (3.29), then takes in the case of the Weyl representation the form of the following two coupled equations:

(3.36a)

(3.36b)

written in matrix form as

(3.37)

As can be seen from these equations, the mixing of the two Lorentz group representations and occurs because of the mass term in the Dirac equation.

Noether currents.

Let us now consider some continuous symmetry transformations on the wave functions, which leave the Lagrangian density invariant. In the infinitesimal limit we then write

(3.38)

The corresponding change in the Lagrange density is then represented by the expression

(3.39)

With the obvious relation

(3.40)

we then have

(3.41)

Using the identity

the second term on the r.h.s. of Equation (3.41) can be rewritten with the result

(3.42)

Now the second term of this equation, set equal to zero, represents the Euler-Lagrange equation as given by Equation (3.14). For, according to the invariance condition of the Lagrange density, we then write

(3.43)

Introducing Noether currents by the defining relation

, (3.44)

Equation (2.43) involves the four-divergence of this quantity for which we thus have

(3.45)

Integrating this expression over the entire ordinary space, and applying Gauss’ theorem to the corresponding three-divergence, with vanishing contribution at the infinite surface, we are left with the expression

. (3.46)

Hence the space integral is a conserved quantity.

In order to interpret this quantity, let us consider the Dirac equation. The corresponding Lagrange density function is given by Equation (3.28). This equation is invariant under the phase transformation, or in infinitesimal form

(3.47)

For Noether’s current we then have, according to Equation (3.44)

(3.48)

and

(3.49)

where we have used the fact that in any representation. As can be seen, represents the probability density, which multiplied by the electron charge, constitutes the charge density. Hence Equation (3.46) expresses the fact that the electric charge of the electron is a conserved quantity.

4. The Dirac Field

As an entrance door to the Dirac field let us consider free particle solutions of the Dirac Equation (3.29). These solutions can be viewed as superpositions of plane waves of the form

with (4.1)

Plugging this expression into Equation (3.29), yields the equation

(4.2)

This equation is most easily solved in the rest frame, where only the component is different from zero, so that we have

(4.3)

where for the Weyl expression (3.35) has been used.

Introducing two-component spinors, the solution is

(4.4)

where the factor has been chosen for future convenience.

Let us now look for a more general solution with two components and and becoming

(4.5)

This solution can be obtained by performing a Lorentz boost on the previous one, which in infinitesimal form can be written as

(4.6)

This relation can be deduced by analogy from the matrix of Equation (3.7) noticing that all spatial directions are equivalent whereas the infinitesimal parameter, called rapidity, replaces the previous.

For finite values of we therefore have

(4.7)

The second expression on the r.h.s. is obtained by expanding the exponential

and noticing that even powers of the matrix yield the unit matrix,

whereas odd ones leave this matrix unchanged.

Now we apply the same boost to the amplitude of Equation (4.1) and write

(4.8)

From the infinitesimal operator as given by Equation (3.24) with I = 3, we deduce the relevant Lorentz transformation operator

(4.9)

Considering the matrix, with the unit matrix, an even

power of the matrix in the exponent of Equation (4.9) yields the unit matrix, whereas an odd one yields this same matrix. The series expansion of the exponential operator of Equation (4.9) therefore leads to the following matrix expression:

(4.10)

Explicitating and adding all matrices, a lengthy but straightforward calculation yields the following diagonal matrix

(4.11)

where the relation

(4.12)

has been used.

We now go back to Equation (4.8) and calculate the amplitude for two

special spinors and, corresponding to spins oriented in the

positive and negative direction respectively. The matrix of Equation (4.11) then immediately yields the results

(4.13a)

(4.13b)

So far we have put the minus sign on the exponent of the defining relation given by Equation (4.1). Consider now the case of a plus sign with

(4.14)

We choose however to maintain and hence. Despite this choice this case corresponds to the negative energy solutions which constitute the famous Dirac sea. This is only apparent if e.g. the Hamilton density is calculated. At this stage we take it only as a known fact.

We are not repeating a calculation similar to the previous one, but indicate only the relations replacing Equation’s (4.13a), (4.13b). For these special situations one finds

(4.15a)

(4.15b)

Defining as usual and, it is instructive to calculate the products, and Considering the special case of Equation (4.13a) we have

With given by Equation (4.13a) we thus obtain

(4.16)

A similar calculation for the case of Equation (4.15b) yields the result

(4.17)

For the case of an arbitrary spin orientation axis we introduce the notations with designating the two opposite spin directions. Then the relations (4.16), (4.17) have to be completed as follows:

(4.18)

. (4.19)

Furthermore we have the relations

, (4.20)

The Hamiltonian.

Starting from the expression (3.28) of the Lagrangian density

and from the expression of the conjugate variable, the Hamiltonian

density is given, according to Equation (2.23) by the expression

More explicitly we then have with and

(4.21)

In the expression of the term thus cancels the first term in Equation (4.21) and we are left with the result

(4.22)

Involving the single particle Hamiltonian

(4.23)

The amplitudes and of Equation’s (4.1) and (4.14) are eigen- functions of this Hamiltonian with eigenvalues and respectively. To see this, multiply the Dirac Equation (3.29) by and write

(4.24)

remembering that.

This equation can be expressed in the form

(4.25)

Replacing by the free-particle expressions of Equation’s (4.1) and (4.14) we then have

(4.26a)

(4.26b)

Introducing these expressions into Equation (4.25) yields the eigenvalue relations stated above

, , (4.27)

with Hence the amplitudes correspond to negative energy solutions which constitute the famous Dirac sea. As in the Klein-Gordon case, this inconvenience is circumvented by means of a fully quantized treatment.

Second quantization.

In replacing the wave function by an operator, we first consider the time-independent Schroedinger operator which, in analogy with Equation (2.40), we write in the form (summation rule with)

(4.28)

or equivalently

(4.29)

Defining an empty state it is understood that we must have

.

Introducing the total Hamiltonian we obtain using Equation (3.22) in the Schoedinger picture

(4.30)

After substituting the expression (4.29) and its adjoint we write

(4.31)

Inverting the order of integration, we take advantage of the relation

and notice that, according to Equation (4.20), the cross terms in the product of the integrand in Equation (4.31) disappear. We are thus left with the expression

(4.32)

where, given the integration over all values of, the replacement has been made.

Eliminating the amplitudes by means of the relations (4.18), (4.19), we thus arrive at the final expression

(4.33)

At this stage it has to be reminded that in the present case of fermions the operators obey anti-commutation relations, which in contrast to the boson relations (2.37), are of the form

(4.34)

This relation allows us to deal with the embarrassing negative energy term in the integrand of Equation (4.33).

Writing by means of the rule stated by Equation (4.34)

(4.35)

we have cast the negative energy into an infinite constant term which can be ignored if the origin of the energy scale is shifted adequately.

A next step consists in interchanging the order of and. This is a trick justified in detail in ref’s [1] [4] [6] . Here we indicate only that it has to do with the fact that in the one-particle case, according to the Pauli principle, we have so that by interchanging, we recover the fundamental relation.

Normal ordering

A procedure of eliminating negative energy terms in the Hamiltonian consists in what is called normal ordering. It means that all operator products are reshuffled in such a way that annihilation operators stand always on the right of creation operators. These operations are symbolically expressed by the letter in front of the products.

Applying this convention to the expression (4.22), supposed second quantized, we thus write

(4.36)

where are time-dependent Heisenberg operators given by the expressions, similar to Equation (4.28) and its conjugate

(4.37a)

(4.37b)

Here the time dependence of the operators has been absorbed into the exponential factors. Moreover, the interchange discussed above, has been taken into account.

A calculation similar to that developed above, with only the cross terms contributing, then leads to the expression

(4.38)

This is exactly the result obtained previously if in Equation (4.35) the infinite negative energy term is ignored and if the operator and state changes discussed there, are accomplished. Thus clearly normal ordering merely integrates these facts.

5. Propagators

The retarded Green’s function.

Let us first consider propagation amplitudes given by the expressions

(5.1a)

(5.1b)

These expressions are obtained by using the fact that in the product of the wave functions of Equation’s (4.37a), (4.37b) only cross terms contribute. This is because in the other terms annihilation operators are on the right and therefore eliminate these terms in the mean values of Equation’s (5.1a), (5.1b). Furthermore the operator relation (4.34) has been accounted for.

We now evaluate the spin sums appearing in Equation’s (5.1a), (5.1b). Using Equation’s (4.13a), (4.13b) and (4.15a), (4.15b) we obtain the following tensor products:

where the relation has been used.

A similar calculation yields

For the spin sum we therefore arrive at the result

(5.2)

It is now an easy matter to show that this matrix is identical with the expression or by extension. Consequently we obtain

(5.3a)

with after a similar calculation

(5.3b)

Making these replacements in the expressions (5.1a), (5.1b) and adding them afterwards, we obtain an anticommutator of the form

(5.4)

with and hence

(5.5)

We now want to link the above commutator to an integral in four space. For this purpose we introduce a quantity defined by the relation

(5.6)

where has now become an integration variable. The integral can be evaluated by considering a closed circuit in the complex plane with two singularities at as shown in Figure 2(a). The corresponding residua are for

for

for the lower clockwise circuit, corresponding to, we therefore obtain for the integral the value

(5.7)

whereas for the upper circuit, corresponding to, the integral is zero.

Inserting the value given by Equation (5.7) into the complete integral given by Equation (5.6) we can, without loss of generality, replace in the second term by and in this way we obtain for

(5.8a)

and for

(5.8b)

Comparing with Equation (5.4) we thus find

(5.9)

where is the Heaviside step function.

Going back to Equation (5.6) we notice that the denominator can be written as. One can also prove that so that in the end we have

(5.10)

Written in the form

(5.11)

this quantity can be regarded as the Fourier transform of

(5.12)

or in Feynman slash notation

(5.12’)

This expression is known as the Dirac propagator. Its Fourier transform represented by Equation (5.10) is a Green’s function of the Dirac operator defined in Equation (3.29). To see this, we first notice that for plane wave states this operator can be written as. Acting with it on the expression given by Equation (5.10) the denominator cancels and we obtain

(5.13)

thus proving the Green’s function relation stated above.

Note however that the integral in Equation (5.10) can be evaluated along different paths. The way chosen so far yields the particular expression (5.9), called the retarded Green’s function. This is because it is only non zero during the time period.

The Feynman propagator.

A different path for evaluating the integral of Equation (5.6) is that shown on Figure 2(b). Designating by the lower circuit, i.e. and by the upper one, i.e., the theorem of residua then yields, instead of Equation (5.7) the following two contributions:

(5.14a)

(5.14b)

Inserting these expressions into Equation (5.6) we obtain the Feynman Green’s function

(5.15a)

(5.15b)

where again in the second line.

Comparing these expressions with Equation (5.4) we see that we have

(5.16)

This can also be written as

(5.17)

where is the time ordering operator which ensures that the earlier time always stands on the right, with the additional condition of a minus sign if the operators are interchanged.

In the Feynman case the integration paths can be slightly modified with respect to those of Figure 2(b) if we replace Equation (5.10) by the expression

(5.18)

With the denominator equal to, the singularities are now shifted

away from the real axis to so that this axis is now entirely part

of the integration paths.

Interpreting Equation (5.18) as a Fourier integral we thus obtain for the Feynman propagator the expression

(5.19)

or in slash notation

(5.19’)

These expressions are basic elements in Many-Body type calculations.

The photon propagator.

In analogy with Equation’s (5.16) and (5.17) representing the Feynman propagator in the Dirac case, we define a photon propagator by the relations

(5.20)

Corresponding to the time-ordered product

(5.21)

Here, are operators of the quantized vector potential according to the expression

(5.22)

The quantities and are polarization vectors labeled by the index in a chosen basis. Let us first consider the product

(5.23)

Postulating the rule

(5.24)

This expression reduces to

(5.25)

with

(5.26)

The value of the quantity depends on the choice of a particular gauge. In the case of the Lorentz-Feynman gauge this value reduces to the metric tensor, as shown in standard textbooks.

As in the Dirac case we now link the expression (5.25) to an integral in 4 dimensional space of the following form:

(5.27)

Performing the integration over along the paths indicated in Figure 2(b) we obtain the two expressions

(5.28a)

(5.28b)

Comparing this with Equation (5.20) we see that the two integrals correspond to the expressions defining the propagator. Finally, as in the Dirac case, the expressions (5.28a), (5.28b) can be obtained by replacing the integral (5.27) by the modified expression

(5.29)

Setting we therefore obtain the expression for the propagator in momentum space

(5.30)

as the final result for the photon propagator in the Lorentz-Feynman gauge.

6. Interacting Fields: The Radiative Electron Mass Shift

Introduction.

Consider an electron in the form of a point charge-e, then the surrounding static electric field possesses the energy

(6.1)

with the Sommerfeld fine structure constant. Recall that through-

out this treatise we use natural units setting

In order to make the integral in Equation (6.1) finite, a lower cut-off radius has to be introduced yielding the value for the energy

(6.2)

In this way the energy tends linearly towards infinity with the cut-off parameter. Applying in a naïve manner Einstein’s relation or in our units, we see that the electromagnetic mass of the electron appears as a linearly diverging quantity.

Attempts have been made to improve things by applying the formalism of quantum field theory to this problem. In this treatise we present a slightly renewed version of these calculations. As a result the linear divergence of the semi-classical theory is brought to the form of a logarithmic one however with no quantitative solution at the end.

The propagators.

Preliminary remark: as is customary in quantum field theory we designate vectors and indices in 4 dimensional Minkowski space by ordinary letters and l.c. greek letters (e.g.) respectively and the corresponding objects in 3 dimensional Euclidean space by bold letters and l.c. Latin letters (e.g.), respectively. Moreover, summation over repeated indices is assumed and furthermore are Dirac’s gamma matrices.

We now consider an electron moving freely through vacuum and define a correlation function by the expression

(6.3)

where and are operators replacing in second quantized theory the usual wave functions.

In expression (6.3) the Dyson operator stands for the time ordered product.

The presence of ground states instead of zero electron states indicates that we are considering interaction of the moving electron with the surrounding electromagnetic vacuum field.

The easiest way for evaluating the correlation function (6.3) consists in applying Feynman rules according to the Feynman diagram of the figure (Figure 3) which shows that the electron-vacuum interaction can be conceived as the emission and reabsorption of a virtual photon visualized by the wavy line.

The elements of this diagram correspond to Feynman propagators in momentum space given by the expressions

(6.4)

for the electron of mass m in momentum state p and k respectively and the propagator expression

(6.5)

for the photon.

In this way during the process the total momentum of the system is conserved at every step. In addition the expressions

, (6.6)

describing the electron-photon interaction have to be inserted at the vertices.

In these expressions the Feynman slash notation abbreviates the sums and, whereas is the metric tensor represented by a 4 dimensional diagonal matrix with,.

Assembling these relations, known as the Feynman rules, we see that the above diagram corresponds to the product

(6.7)

where the relation has been used. Noticing that in both the Weyl and the Dirac representation the sum is equal to 4 times the unit matrix, we condense the expression (6.7) into the form

(6.8)

where the central part is given by the expression

(6.9)

after adding an integration over all possible intermediate 4 momenta.

The index on indicates that the application of the above diagram represents in fact a limitation to second order of a perturbation expansion. An extension to all orders under special conditions will be discussed below.

The integration procedure.

Before starting the integration in the expression for we use Feynman’s trick based on the identity

Comparing with Equation (6.9) we thus write the integral in the form

(6.10)

Following a common procedure we now change variables according to the relation

(6.11)

Then the parenthesis in the denominator of the integrand takes the form

(6.12)

An essential simplification arises if we restrict ourselves to the zero’th order contribution in with

(6.13)

The integral in (6.10) then reduces to

(6.14)

Note that the same letter matrices as well as scalars recognizable from the context.

Separating the part from the space part and extending the integral over components from to, the term in the numerator does not contribute and we are left with the expression

(6.15)

where now all matrices are replaced by scalars.

The evaluation of the second integral is presented in Appendix leading to the result

(6.16)

Setting and introducing an upper limit cut-off we replace the expression (6.16) by the following integral

(6.17)

Introducing the dimensionless variable we also have

(6.18)

with the limiting expression

(6.18’)

where we have assumed that the cut-off value is large as compared to unity.

Plugging this result into Equation (6.9) we thus arrive at the final expression

(6.19)

Renormalization.

Let us suppose that the change in the correlation function represented by the resulting expression (6.19) can be reproduced by renormalizing the mass in the free electron propagator, i.e. by adding a correction to the initial mass. Assuming this correction sufficiently small we then consider the expansion

(6.20)

Equating the correction term with the expression (6.8) with the expression (6.19) for inserted, we have

(6.21)

Approximating on the r.h.s. by its dominant part

Equation (6.21) yields the result [7] [8]

(6.22)

This is the result derived in the literature by various methods, showing that the fully quantized theory reduces the linear convergence of the classical expression (6.2) to a logarithmic one.

Discussion.

There seems to be no indication how to estimate the cut-off parameter Clearly the logarithmic divergence makes the mass shift less sensitive to the value of this parameter. Moreover it can be argued that a large mass shift should show up in experiments. Nevertheless, in order to get a number out of the calculations, one could for instance consider the fact that the proton mass constitutes a natural upper limit on the mass scale of conventional particles. Identifying it with would lead to the result:

a number that seems realistic. Naturally this estimation has to be taken merely as an example among others that one could imagine.

However, despite the fact that the true numerical value of the electromagnetic electron mass shift is as yet unknown, its correct qualitative evaluation, as reviewed in this section undoubtedly constitutes an important fact.

Zitterbewegung

The fact that quantum field calculations lead to a logarithmic divergence of the electron self-energy instead of the linear classical result of Equation (6.2), can be understood if one takes into account the spread of the electron position due to quantum fluctuations [7] . This is equivalent with attributing the electron a finite dimension of the order of the Compton wavelength, whereas classically the electron is point like. More generally, quantum fluctuations of a particle position of the order of are known as Zitterbewegung. It is this effect that we are studying now in the stationary case.

In order to determine the position occupied in the average by the electron with respect to some central position, let us consider the propagator product

(6.23)

Interpreting the central part

(6.24)

as a density operator we obtain the desired average by taking a trace represented fomally by the expression

(6.24a)

Writing out explicitly the product of (6.23) we obtain from the defining relation (5.14) the result

(6.25)

under the condition

(6.25a)

Furthermore, the variable can be specialized as so that the condition (6.25a) becomes With these simplifications the product of (6.25) reduces to

(6.26)

The taking of the trace in Equation (6.24a) amounts to integrating over the variable y and afterwards replacing the matrix by the scalar. The resulting delta function then leads to the result

(6.27)

The integral of Equation (6.27) is elementary, yielding with the result

(6.28)

With the last integral on the r.h.s being equal to, we obtain for the

probability the final result

(6.29)

As a test we integrate over the entire space and find

(6.30)

thus proving the validity of our probability calculation.

Clearly a distribution as represented by Equation (6.29) will lead to a softer divergence than one of the type corresponding to the non relativistic case. We want however to emphasize that the electron is still regarded as a point particle, but one that giggles around some central position producing an apparent spread of its mass.

7. The Electron-Electron Scattering (MLLER) Amplitude and Its Yukawa Analog

Consider scattering involving two particles and introduce a scattering matrix in the form

(7.1)

where the second term describes the scattering process.

Assuming that the particles have incident momenta and respectively and outgoing momenta and, momentum conservation demands that matrix elements of satisfy the relation

(7.2)

where is the scattering amplitude which is of interest here. In the fully quantized theory interaction takes place by means of the exchange of a virtual particle of momentum q.

We specialize now to the case of two colliding electrons schematically represented by the Feynman diagram below.

We write the Hamiltonian of the system in the form

(7.3)

where is the part belonging to the free electrons and that of the interaction during the scattering. In second quantized Dirac theory this latter part is given by the expression

(7.4)

with, the electron field operators in the Heisenberg picture and the vector potential operator of the electromagnetic field present in the system.

The relevant contribution here is the second order term in the perturbation expansion of the matrix involving the quantity.

Given the interaction Hamiltonian of Equation (7.4) this term contains the time-ordered product

(7.5)

with T the familiar time ordering operator. Note that a factor 1/2 from the exponential expansion is left out since it is compensated for by adding identical expressions with and interchanged. In order to evaluate the above product we apply Wick’s theorem [1] reducing it to a product of the contracted e-m field operators with the remaining factors put into normal order. Thus we write

(7.6)

Substituting into the parenthesis the expressions derived in section (3) for and we obtain an operator product of the form

(7.7)

At this stage we suppress for simplicity spin labels on the operators and functions.

Putting in the expression (7.7) the operators in normal order we make the replacement

(7.8)

We now take matrix elements between states

(7.9a)

(7.9b)

Together with the preceding sequence of Equation (7.8) this generates the new operator sequence

(7.10)

We now make use of operator commutation relations which yield the equations

(7.11)

similarly for etc i.e. 4 equations.

Now after integrating in Equation (7.7) over the variables the and factors disappear and we are left with the expression

(7.12)

Going back to Equation (7.6) and recalling that the contraction of vector potential operators is equivalent with the propagator expression

(7.13)

we obtain the matrix element in the form

(7.14)

Identifying the integrals as times delta functions so that

, the expression (7.14) reduces to

(7.15)

Comparing this expression with the defining relation (7.2) we find for the electron-electron scattering amplitude the formal expression

(7.16)

The non-relativistic limit.

In the non relativistic limit where it is assumed that the kinetic energy of the electrons is small as compared to, i.e. to, the spinors derived in section 3 reduce to the simple form

, (7.17)

with equal to or.

Then for we have

, (7.18)

with and, in the Weyl representation,

The products in Equation (7.16) are

(7.19a)

(7.19b)

Furthermore we have in this approximation with

(7.20)

Thus the amplitude of Equation (7.16) reduces to

(7.21)

Now clearly, labeling the spins by in the x term and by in the term, the products reduce to the Kronecker symbol and respectively, meaning that the spin is conserved during the process. Therefore Ignoring the spin labels and setting we write for the scattering amplitude

(7.22)

Consider now the electrostatic potential of the system and its Fourier transform defined by the relation

(7.23)

In the case of a Coulomb potential

(7.24)

An elementary integration yields the result

(7.25)

Comparing this result with Equation (7.22) one sees that the amplitude factor is proportional to the Coulomb potential in the representation. This shows that it is equivalent to the ordinary quantum mechanical solution of the scattering problem in the Born approximation.

For the sake of completeness we indicate the link between the amplitude and the differential cross section. In the center of mass frame the following relation holds:

(7.26)

Substituting for the expression (7.22) we thus obtain

(7.27)

Note that this expression is equal to the celebrated Rutherford formula which applies to scattering of a particle in a static Coulomb field.

The Yukawa potential.

An approach similar to that leading to the Coulomb potential, treated in terms of the exchange of a photon between two electrons, has been proposed by Yukawa in 1935 for the interpretation of nuclear forces. Here the interaction takes place between heavy particles of mass, i.e. nucleons, and for the binding the photon is replaced by a massive particle of mass much smaller than called meson.

The calculation can be deduced from the previous one by replacing the photon

propagator by the meson propagator with the four momentum

of the meson and the electro-magnetic interaction replaced by a quantity designed as. The result which replaces that of Equation (7.16) is then

(7.28)

In the non-relativistic limit one finds

with (7.29)

Connecting in this limit the scattering amplitude to the potential in the representation one has

(7.30)

with in the representation

(7.31)

Setting;, the integral can be done easily, leading to the result

. (7.32)

This attractive potential is short ranged as compared with the Coulomb potential. The presence of the exponential factor yields for this range the value

, which is of the order of 1 fm if for the meson mass is inserted.

Although the Yukawa model has been replaced since by more evolved concepts, it still provides insight into the nature of nuclear forces.

8. Vacuum Polarization

The photon self energy.

Consider a photon propagating freely in vacuum. If its interaction with the vacuum field is taken into account, a situation represented by the Feynman diagram below will be present. During the propagation there will be emission/absorption of a virtual electron/positron pair at one vertex and afterwards the inverse process will occur at the other vertex.

The difference with respect to the case without interaction involves a tensor which in second order will be written as with the four momentum of the photon. For this tensor, by applying Feynman rules, in [1] the following expression has been derived:

(8.1)

Applying, as in the electron case, the Feynman trick and setting afterwards

(8.2)

one arrives at the expression

(8.3)

where terms linear in have been omitted.

In [1] a Wick rotation has been applied to this integral with the result

(8.4)

with

(8.5)

This integral is ultraviolet diverging. It can be simplified by using the tensorial relation

(8.6)

involving the scalar quantity Comparing for Equation’s (8.4) and (8.6) we obtain for this quantity the expression

(8.7)

Assuming now, making in (8.5) the approximation and performing the integration over we find

(8.8)

For the integral on the r.h.s. we have, according to [1] , the expression

(8.9)

The remaining integral is logarithmically ultraviolet diverging. Let us calculate it however formally as follows:

Pauli-Villars regularization.

The Pauli-Villars regularization consists in making the integral convergent by subtracting the same expression but with replacing and. This immediately yields

(8.10)

The integral of Equation (8.9) thus becomes

(8.11)

For the quantity of interest we therefore find

(8.12)

Considering as a cutoff value, designated from now on as, we finally obtain [7] [8]

(8.13)

with the fine structure constant.

Charge renormalization.

Going back to the electron-electron scattering problem clearly the photon self-energy effect just discussed, will manifest itself as a modification of the photon propagator represented by the wavy line in Figure 4, which therefore has to be replaced by the configuration of Figure 5. One then expects that the global effect corresponds to the scalar quantity which, with the approximations made, takes a constant value given by Equation (8.13). Designating this value by the letter, then in the case of non-relativistic electron-electron scattering the amplitude is reduced by a factor. Obviously this is equivalent to a renormalization of the electric charge which is thus diminished by a factor. Due to this effect the vacuum behaves like a polarizable medium capable of producing what is known as vacuum polarization. Note that a vacuum containing electron-positron pairs represents an analogy with ordinary dipole polarizable media.

The amended Coulomb potential

Having treated the diverging expression in (8.7) by means of a regularization procedure, we are now going to extract from this expression a term which is independent of any cut-off parameter. For this purpose we make the following first order expansion:

(8.14)

where we have set

(8.15)

assuming in accordance with the previous condition Focussing on the second term inside the parenthesis in Equation (8.14), which yields the non diverging contribution, we replace Equation (8.7) by the expression

(8.16)

where the equivalence has been used.

Expliciting now and according to Equation (8.15), we write

(8.17)

With the values of the integrals equal respectively to and we thus

find

(8.18)

which is indeed the value found in the literature.

Atomic energy level shift

Consider now the Coulomb potential as given in space by Equation (7.25). Its modification due to vacuum polarization produces a relative change equal to so that according to Equation (8.18) we have

(8.19)

Taking the inverse Fourier transform yields for the amended potential in space the expression

(8.20)

Applying this potential to electrons inside an atom will lead to a shift of energy levels obtained by multiplying the correction term with the electron density function and space integration. The effect then becomes proportional to showing that only s levels will be affected. In the case of hydrogen the effect represents a small part of the Lamb shift. Larger effects can be predicted in the case of muonic atoms, i.e. atoms where the electrons are replaced by mesons [9] .

For numerical values of the expected or measured shifts we are referring to the abundant literature on this subject.

9. Conclusion

In this treatise we are interested in phenomena involving the presence of what is sometimes called the physical vacuum. To deal with these effects, one adopts the field viewpoint, which consists of replacing for elementary particles, e.g. electrons, wave functions by operators acting on physical vacuum states. Interactions between fields defined in this way are then treated according to Feynman’s propagator method. The main difficulty affecting this method is the appearance of divergencies which are dealt with by means of two specific procedures known as regularization and renormalization. The first one consists of making expressions finite by applying e.g. cut-off or Pauli-Villars regularization. The second one is a redefinition of physical quantities, e.g. electric charge or mass, in accordance with the finite results previously obtained. In this treatise, we consider mainly results for the electron self-energy and the vacuum polarization case. Some of our derivations of these results are original and special attention is given to their interpretation in terms of the underlying physical facts.

Acknowledgements

Particular thanks go to Prof. Gillian Peach and to Prof. Cynthia Kolb Whitney for reading and improving the manuscript.

Cite this paper

Schuller, F., Neumann-Spallart, M. and Savalle, R. (2017) Guidelines to Quantum Field Interactions in Vacuum. Journal of Modern Physics, 8, 382-424. https://doi.org/10.4236/jmp.2017.83026

References

Appendix

Evaluation of the integral

(A1)

Setting we write

(A2)

With the change of variables

(A3)

The integral in (A2) takes the form

(A4)

where we have deliberately not specified the integration limits.

Introducing the identity

we ignore the principal value which in a more detailed treatment can be proven to yield zero. With the delta function inserted the expression (A4) then reduces to

(A5)

Performing the derivation as indicated in Equation (A2) and replacing the intermediate parameter A by its value leads to the desired result

(A6)