Journal of Modern Physics
Vol.08 No.01(2017), Article ID:73626,12 pages
10.4236/jmp.2017.81008
Bell’s Non-Locality Theorem Can Be Understood in Terms of Classical Thermodynamics
Tomofumi Miyashita
Miyashita Clinic, Mitsuya-kita, Yodogawa-ku, Osaka, Japan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 30, 2016; Accepted: January 17, 2017; Published: January 20, 2017
ABSTRACT
Bell’s non-locality theorem can be understood in terms of classical thermodynamics, which is already considered to be a complete field. However, inconsistencies in classical thermodynamics have been discovered in the area of solid-oxide fuel cells (SOFCs). The use of samarium-doped ceria electrolytes in SOFCs lowers the open- circuit voltage (OCV) to less than the Nernst voltage. This low OCV has been explained by Wagner’s equation, which is based on chemical equilibrium theory. However, Wagner’s equation is insufficient to explain the low OCV, which should be explained by fluctuation and dissipation theorems. Considering the separation of the Boltzmann distribution and Maxwell’s demon, only carrier species with sufficient energy to overcome the activation energy can contribute to current conduction, as determined by incorporating different constants into the definitions of the chemical and electrical potentials. Then, an energy loss equal to the activation energy will occur because of the interactions between ions and electrons. This energy loss means that an additional thermodynamic law based on an advanced model of Maxwell’s demon is needed. In this report, the zero-point energy can be explained by this additional thermodynamic law, as can Bell’s non-locality theorem.
Keywords:
Wagner’s Equation, Fluctuation and Dissipation Theory, Boltzmann Distribution, Maxwell’s Demon, Additional Thermodynamic Law

1. Introduction
Solid-oxide fuel cells (SOFCs) directly convert the chemical energy of fuel gases, such as hydrogen and methane, into electrical energy. SOFCs use a solid-oxide film as the electrolyte, and oxygen ions serve as the main charge carriers. Typically, yttria-stabilized zirconia (YSZ) is used as the electrolyte material in these cells. The operating temperature of these cells (873 - 1273 K) should be reduced to extend their life spans. Therefore, the use of mixed ionic and electronic conducting (MIEC) electrolyte materials, such as samaria-doped ceria (SDC) electrolytes, at lower temperatures is preferred. The open- circuit voltage (OCV) of an SDC cell is approximately 0.8 V, which is lower than the Nernst voltage (Vth) of 1.15 V at 1073 K. This low OCV is attributed to the low value of the ionic transference number (tion). The low OCV has been calculated using Wagner’s equation, which is based on chemical equilibrium theory [1] [2] . However, there are serious problems in Wagner’s equation [3] - [8] . We discuss these problems in Section 2.
Over the past two decades, the understanding of nonequilibrium thermodynamics has been enhanced by fluctuation and dissipation theorems such as the Jarzynski and Crooks relations [9] [10] . Attempts have been made to explain Maxwell’s demon based on fluctuation and dissipation theorems [11] . We discovered the following empirical equation using SDC electrolytes [12] :
 (1)
(1)
where 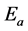 is the ionic activation energy, which is 0.7 eV for SDC electrolytes. Therefore, the OCV in Equation (1) is
is the ionic activation energy, which is 0.7 eV for SDC electrolytes. Therefore, the OCV in Equation (1) is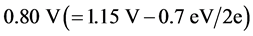 . Equation (1) can be explained using an advanced model of Maxwell’s demon. On the basis of this model, we proposed an additional thermodynamic law. We previously discussed the relationship between quantum physics and this additional thermodynamic law [8] . In Section 3, we discuss a prototypical and an advanced model of Maxwell’s demon in relation to hopping conduction.
. Equation (1) can be explained using an advanced model of Maxwell’s demon. On the basis of this model, we proposed an additional thermodynamic law. We previously discussed the relationship between quantum physics and this additional thermodynamic law [8] . In Section 3, we discuss a prototypical and an advanced model of Maxwell’s demon in relation to hopping conduction.
Then, the inevitable energy dissipation equal to  from the particles to the environment will occur as the zero-point energy. Consequently, the space uses not the prototypical model of Maxwell’s demon using YSZ electrolytes but rather the advanced model of Maxwell’s demon using SDC electrolytes. In Section 4, we discuss the relationship between the zero-point energy and this additional thermodynamic law.
from the particles to the environment will occur as the zero-point energy. Consequently, the space uses not the prototypical model of Maxwell’s demon using YSZ electrolytes but rather the advanced model of Maxwell’s demon using SDC electrolytes. In Section 4, we discuss the relationship between the zero-point energy and this additional thermodynamic law.
Bell’s theorem [13] is a “no-go theorem” that draws a distinction between quantum mechanics and classical mechanics. Bell’s theorem states that “No physical theory of local hidden variables can reproduce the predictions of quantum mechanics.” However, Bell did not know that the information of local hidden variables could be erased during measurement due to the inevitable energy dissipation. In Section 5, based on the advanced model of Maxwell’s demon, we show that Bell’s non-locality theorem can be explained in terms of classical thermodynamics. Furthermore, a determination experiment to disprove quantum teleportation is proposed. Bell’s non-locality theorem can be local with this additional thermodynamic law.
2. Problems in Chemical Equilibrium Theory
The low OCV has been explained by Wagner’s equation, which is based on chemical equilibrium theory. The flux of oxygen ions under open-circuit conditions, as described by Wagner’s equation [1] [2] , is
 (2)
(2)
where  and
and  are the
are the 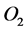 flux and the
flux and the 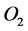 partial pressure, respectively;
partial pressure, respectively; 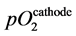 and
and  are the
are the 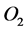 partial pressures at the cathode and the anode, respectively; R, T, and F are the gas constant, the absolute temperature, and Faraday’s constant, respectively; L is the thickness of the membrane or film; and
partial pressures at the cathode and the anode, respectively; R, T, and F are the gas constant, the absolute temperature, and Faraday’s constant, respectively; L is the thickness of the membrane or film; and 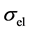 and
and  are the conductivities of the electrons and oxygen vacancies, respectively.
are the conductivities of the electrons and oxygen vacancies, respectively.
From Equation (2), Equations (3) and (4) can be deduced [14] .
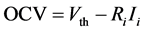 (3)
(3)
where Ri and Ii are the ionic resistances of the electrolyte and the ionic current, respectively.
 (4)
(4)
Equation (4) is often used when 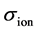 is constant under various
is constant under various  partial pressures [14] , and Ii is not apparently expressed. When an SOFC is operated under OCV conditions, the electronic leakage current (Ie) is defined using the external current (Iext):
partial pressures [14] , and Ii is not apparently expressed. When an SOFC is operated under OCV conditions, the electronic leakage current (Ie) is defined using the external current (Iext):

In general, Ii and Ie are not zero. Parameter tion is expressed as

However, σel is a function of the 

where 

Problem 1: The calculated OCV will always be higher than the experimental result. Polarization voltage losses are frequently used to compensate, but the lack of change of the OCV during electrode degradation is impossible to explain [3] [4] [5] .
Problem 2: The equilibration process of thick SDC electrolytes in response to a change in the anode gas cannot be explained because the response from the experimental results is too fast to explain the delay in the electron diffusion current from the cathode to the anode [6] .
To solve the aforementioned problems, there should be a fast response current- independent constant anode voltage loss (
3. Prototypical and Advanced Model of Maxwell’s Demon in Relation to Hopping Conduction
3.1. Prototypical Model of Maxwell’s Demon in Relation to Hopping Conduction
YSZ is a ceramic in which the crystal structure of zirconium dioxide is made stable by the addition of yttrium oxide. When yttria is added to pure zirconia, Y3+ ions replace Zr4+ on the cationic sublattice. Oxygen vacancies are generated due to the charge neutrality. A graphical explanation is provided in Figure 1. Ionic conduction involves
Figure 1. Graphical explanations for generating oxygen vacancies. Oxygen vacancies are generated because of charge neutrality. Quoted from Yttria-stabilized zirconia (Wikipedia). https://en.wikipedia.org/wiki/Yttria-stabilized_zirconia
hopping from an occupied site (8c site) to a vacant lattice site (8c). Oxygen ions then pass through the first gate (32f site) and the second gate (another 32f site) [17] . A sche- matic of the path for ions is shown in Figure 2. The situation is very similar to that of a prototypical model of Maxwell’s demon. Landauer first proposed the principle of this model in 1961. Landauer’s principle states that, if an observer loses information about a physical system, the observer loses the ability to extract work from that system [18] .
3.2. Advanced Model of Maxwell’s Demon in Relation to Hopping Conduction
YSZ electrolytes are purely ionic conductors; however, SDC electrolytes are MIEC materials. Interactions should occur between hopping ions and electrons. A schematic of the path for ions in SDC electrolytes is shown in Figure 3. Gabor and Brillouin independently proposed the energy loss during interactions [19] [20] . Hence, the situation is different from the use of YSZ electrolytes, which can be explained by Landauer’s principle [18] .
In previous work, we explained the advanced model of Maxwell’s demon electrochemically [6] [8] . The Boltzmann distribution of oxygen ions in the electrolyte at 1073 K is displayed in Figure 4. The ions with energies exceeding the ionic activation energy become carriers (hopping ions). Figure 5 presents an incorrect carrier distribution. The Boltzmann distribution cannot be separated using passive filters, and an accurate distribution is provided in Figure 6. The loss of Gibbs energy is illustrated in Figure 5, and the real Gibbs energy (Greal) should be determined using Equation (8) [6] :

Then, voltage losses occur during every hopping process in the MIEC area. Therefore, the voltage loss resulting from only four hopping processes (

Figure 2. Schematic of the path for ions in YSZ electrolytes. The situation is very similar to that of a prototypical model of Maxwell’s demon explained by Landauer’s principle.
Figure 3. Schematic of the path for ions in SDC electrolytes. Interactions should exist between the hopping ions and electrons, as explained by Gabor and Brillouin.
Figure 4. Boltzmann distribution at 1073 K. Ions with energies exceeding the ionic activation energy are converted into charge carriers (i.e., hopping ions).
Figure 5. Forbidden distribution of hopping ions. This distribution is forbidden according to “Maxwell’s demon.”
Figure 6. Correct distribution of hopping ions. The shape of the distribution in this figure should be the same as the shape of the distribution in Figure 4.

The Jarzynski equality is [7]

where the over-line indicates an average over all possible realizations of an external process that takes the system from the equilibrium state A to a new nonequilibrium state under the same external conditions as that of the equilibrium state B.
Ions in equilibrium state A lose energy (=0.7 eV) during their hopping in the MIEC electrolyte, and the heating of the colder ions can occur immediately in the vacancies. However, after the last hop, the ions cannot be heated and therefore exit the electrolyte in equilibrium state B. A schematic of this explanation of the energy loss is shown in Figure 7. Consequently, Equation (1) is compatible with the second law of thermodynamics.
3.3. Additional Thermodynamic Law Based on the Advanced Model of Maxwell’s Demon
The electrochemical potential can be separated into the chemical potential and the electrostatic potential,

where zi, ηi, μi and 


where N, 




Figure 7. Schematic of the explanation for the energy loss. Equation (1) can be compatible with the Jarzynski equality.
The electrical potential (
“Considering the separation of the Boltzmann distribution and Maxwell’s demon, only carrier species with sufficient energy to overcome the activation energy can contribute to current conduction, as determined by incorporating different constants into the definitions of the chemical and electrical potentials. Then, an energy loss equal to the activation energy will occur because of the interactions between ions and electrons.”
Using S (the action function), we can state the Nernst-Planck equation as

From the principle of least action,

Considering the separation of the Boltzmann distribution and Maxwell’s demon, the generalized expression obtained from Equations (12) and Equation (13) is

Equation (17) holds for one hop but not zero when Ea is not zero. In SDC electrolytes, the energy loss during hopping due to inevitable dissipation (Eloss) is

3.4. Determination Experiment for an Advanced Model of Maxwell’s Demon
Oxygen ions transport through a path during hopping in the lattice structure. The electric potential in the path during hopping differs from the electric potential in the vacancies. In YSZ electrolytes, which are purely ionic conductors, ions do not lose energy. However, in SDC electrolytes, which are MIEC materials, the ions lose a large amount of energy. However, measuring the electric potential during hopping is difficult. We thus propose a determination experiment. A negatively charged metal ball (N-ball) and positively charged heavy metal balls (P-balls) should all be coated with plastic. Using springs, the three P-balls can be connected with each other, and then the N-ball can go through the center of them at high speed under vacuum. The speed of the N-ball may be unchanged after the collision. However, when an ionized gas spray is used during the collision, the speed of the N-ball will become small. The energy loss of the N-ball can be controlled by changing the spring constant. A schematic of the explanation of this determination experiment is shown in Figure 8.
4. Explanation of the Zero-Point Energy in Terms of Classical Thermodynamics
Equation (17) and Equation (18) form the generalized expression of the additional thermodynamic law. In quantum physics, instead of



where 

Equation (20) indicates that, when the separation of the Boltzmann distribution by 



5. Bell’s Non-Locality Theorem Can Be Understood in Terms of Classical Thermodynamics
5.1. Bell’s Non-Locality Theorem
Bell’s theorem is a “no-go theorem” that draws a distinction between quantum mechanics and classical mechanics [13] . Bell’s theorem states, “No physical theory of local hidden variables can reproduce the predictions of quantum mechanics.”
The inequality that Bell derived can then be written as

where 
Figure 8. Schematic of the explanation of the determination experiment for an additional thermodynamic law. When an ionized gas spray is used during the collision, the speed of the N-ball will become small. The energy loss of the negatively charged metal ball can be controlled by changing the spring constant.
proven by considering a system of two entangled qubits. The examples concern systems of particles that are entangled in spin. Quantum mechanics allows predictions of correlations that would be observed if these two particles have their spin measured in different directions.
However, Bell was unaware of the inevitable energy dissipation during the measurement. According to Brillouin [20] , information means negative entropy (negentropy), which should be erased during the observation. Hence, the information of local hidden variables can be erased during the inevitable energy dissipation.
5.2. Confounding Factor of the Inevitable Energy Dissipation
In statistics, a confounding factor is an extraneous factor in a statistical model that correlates with both the dependent variable and the independent variable in a way that explains away some of the correlation between these two variables.
When there should be inevitable energy dissipation from particles to the environment during the measurement, combined with the relative theory, the total angular momentum of two entangled qubits cannot be conserved after the measurement. We propose the following confounding factor based on locality.
Confounding factor: Spin is similar to a vector quantity that has a direction as the local hidden variable. However, the information of the direction can be erased because of the inevitable energy dissipation during the measurement. This information refers to spin in the positive or negative direction of the chosen axis after the measurement.
5.3. Calculation of Correlation Coefficient Considering the Confounding Factor Based on Locality
We consider a photon. The frequency of photons is much higher than that of radio waves. Within radio waves, AM broadcasting is the process of radio broadcasting using amplitude modulation and FM broadcasting uses frequency modulation. In principle, we can manipulate photons using amplitude modulation and frequency modulation. When the angle between a vector quantity and the chosen axis is



Then, the rest of the information I1 between 


Thus, I1 is determined only by 



In general, because of rotational symmetry, Equation (24) should be rewritten as

In the experiment performed by Aspect [22] , the definition of 


Consequently, Bell’s non-locality theorem can be understood in terms of classical thermodynamics.
5.4. Determination Experiment for Local Hidden Variables Considering a Confounding Factor Based on Locality
We proposed a determination experiment for local hidden variables, which is combined with the experiment of Aspect and a double-slit experiment. The source S produces pairs of photons, which are sent in opposite directions. After the detection of the left photons, the right photon receives the information of its position by quantum teleportation. Then, an interference pattern cannot be created on the screen behind the double slit. A schematic of the determination experiment for the local hidden variables is shown in Figure 9. When an interference pattern is observed, quantum teleportation (non-locality) will be denied.
6. Summary
Inconsistencies in classical thermodynamics have been discovered in the area of SOFCs. The use of SDC electrolytes in SOFCs lowers the OCV to less than the Nernst voltage. This low OCV has been explained by Wagner’s equation, which is based on chemical equilibrium theory. However, Wagner’s equation is insufficient to explain the low OCV. By considering the separation of the Boltzmann distribution and Maxwell’s demon, we proposed an additional thermodynamic law based on an advanced model of Maxwell’s demon. The zero-point energy can be explained by this additional thermodynamic law. Then, inevitable energy dissipation equal to 
Figure 9. Schematic of the determination experiment for local hidden variables. The source S produces pairs of photons, which are sent in opposite directions. After the detection of the left photons, the right photon receives the information by quantum teleportation. When an interference pattern is observed, quantum teleportation (non-locality) will be denied.
Maxwell’s demon. Bell’s non-locality theorem can be explained by this additional thermodynamic law. Spin is similar to a vector quantity with direction as a local hidden variable. According to Brillouin, the information of the direction can be erased because of the inevitable energy dissipation during the measurement. We proposed a determination experiment for local hidden variables, which was combined with the experiment by aspect and a double-slit experiment. When an interference pattern is observed, quantum teleportation (non-locality) will be denied. Bell’s non-locality theorem can be local with this additional thermodynamic law.
Cite this paper
Miyashita, T. (2017) Bell’s Non-Locality Theorem Can Be Understood in Terms of Classical Thermodynamics. Journal of Modern Physics, 8, 87-98. http://dx.doi.org/10.4236/jmp.2017.81008
References
- 1. Wagner, C. (1975) Progress in Solid State Chemistry, 10, 3-16.
https://doi.org/10.1016/0079-6786(75)90002-3 - 2. Bouwmeester, H.J.M. and Burggraaf, A.J. (1997) Dense Ceramic Membranes for Oxygen Separator. In: Gellings, P.J. and Bouwmeester, H.J.M., Eds., The CRC Handbook of Solid State Electrochemistry, CRC Press, New York, 481-553.
https://doi.org/10.1201/9781420049305.ch14 - 3. Miyashita, T. (2006) Journal of Materials Science, 41, 3183-3184.
https://doi.org/10.1007/s10853-006-6371-8 - 4. Miyashita, T. (2011) Electrochemical and Solid-State Letters, 14, 1-4.
https://doi.org/10.1149/1.3581208 - 5. Miyashita, T. (2014) ECS Transactions, 59, 53-61.
https://doi.org/10.1149/05901.0053ecst - 6. Miyashita, T. (2017) ECS Transactions, 75,1-24.
http://ecst.ecsdl.org/content/75/54/1.full.pdf+html - 7. Miyashita, T. (2011) Materials Sciences and Applications, 2, 180-186.
https://doi.org/10.4236/msa.2011.23022 - 8. Miyashita, T. (2011) Journal of Modern Physics, 2, 26-29.
https://doi.org/10.4236/jmp.2011.21005 - 9. Jarzynski, C. (1997) Physical Review Letters, 78, 2690-2693.
https://doi.org/10.1103/PhysRevLett.78.2690 - 10. Crooks, G.E. (1999) Physical Review E: Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 60, 2721-2726.
https://doi.org/10.1103/PhysRevE.60.2721 - 11. Sagawa, T. and Ueda, M. (2007) Jarzynski Equality with Maxwell's Demon. arXiv: cond-mat/0609085.
https://arxiv.org/abs/cond-mat/0609085v3 - 12. Miyashita, T. (2005) Journal of Materials Science, 40, 6027.
https://doi.org/10.1007/s10853-005-4560-5 - 13. Bell, J. (1964) Physics, 1, 195-200.
http://cds.cern.ch/record/111654/files/vol1p195-200_001.pdf - 14. Rickert, H. (1982) Electrochemistry of Solids—An Introduction. Springer, Berlin.
https://doi.org/10.1007/978-3-642-68312-1 - 15. Kudo, T. (1997) Survey of Types of Solid Electrolytes. In: Gellings, P.J. and Bouwmeester, H.J.M., Eds., The CRC Handbook of Solid State Electrochemistry, CRC Press, New York, 195-221.
https://doi.org/10.1201/9781420049305.ch6 - 16. Dalslet, B., Blennow, P., Hendriksen, P.V., Bonanos, N., Lybye, D. and Mogensen, M. (2006) Journal of Solid State Electrochemistry, 10, 547-561.
https://doi.org/10.1007/s10008-006-0135-x - 17. Boyapati, S., Wachsman, E.D. and Jiang, N. (2001) Solid State Ionics, 140, 149-160.
https://doi.org/10.1016/S0167-2738(01)00698-1 - 18. Landauer, R. (1961) IBM Journal of Research and Development, 5, 183-191.
https://doi.org/10.1147/rd.53.0183 - 19. Gabor, D. (1964) Progress in Optics, 1, 111-153.
http://www.sciencedirect.com/science/article/pii/S0079663808706097 - 20. Brillouin, L. (1951) Journal of Applied Physics, 22, 334-337.
https://doi.org/10.1063/1.1699951 - 21. Grossing, G. (2004) Foundations of Physics Letters, 17, 343-362.
https://arxiv.org/abs/quant-ph/0205047v6 - 22. Grangier, A., Aspect, A. and Roger, P. (1982) Physical Review Letters, 49, 91-94.
https://doi.org/10.1103/PhysRevLett.49.91










