Received 5 October 2015; accepted 26 December 2015; published 29 December 2015

ABSTRACT

The universal expression for the amplitude square 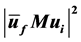for any matrix of interaction M is derived. It has obvious covariant form. It allows the avoidance of calculation of products of the Dirac’s matrices traces and allows easy calculation of cross-sections of any different processes with polarized and unpolarized particles.

Keywords:

Quantum Electrodynamics, Amplitude Square, Polarized Particles

1. Introduction

Amplitude square calculations are necessary in order to find probability transactions for any processes

in quantum electrodynamics. The interaction matrix M is the combination of the Dirac matrices and their products. This circumstance causes very labor-intensive calculation even if the Feynman technique of trace of matrix products calculation is used [1] . When polarization of in- and out-particles is taken into account corresponding calculations are especially labor-intensive. That is why such calculations often do not take particle polarization

into account. Usually for each particular process is calculated separately. There are many papers devoted to calculation of for a particular process.

However, all interaction matrices have the same structure and set of permissible matrices is restricted. Any 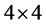matrix can be represented as

(1)

Here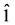―unit matrix,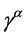―four Dirac’s matrices, 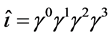, , 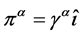, 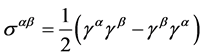I

and J―scalar and pseudoscalar, 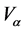and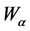―vector and pseudo-vector,―anti-symmetrical tensor.

In- and out-fermions are represented by Dirac’s bispinors of the same type:

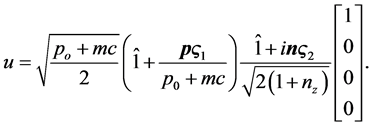(2)

Here, ,―three-dimensional unit spin pseudo- vector in particle’s own reference frame,. In particles’ own reference frame its linear momentum is zero. For the bispinor the relativistically covariant normalization is used.

Thus the possible choices for are restricted. So, for all of them can be calculated and a

universal expression can be derived. This expression can be used for all possible interaction matrices. Similar problem was discussed in [2] . Unfortunately, that expression was almost impossible to use for practical purposes because it was expressed in terms of vector parametrization of Lorentz’s group. Also such expression was dis-

cussed in [3] but was expressed through the three-dimensional quantities in laboratory reference frame. In most cases it is preferable to have Lorentz’s covariant expression which is derived below.

2. Covariant Expression for Amplitude Square

Let us write as and use the equality:

(3)

Here

(4)

Which leads to:

(5)

Let us take into account that for the bispinor (2)

(6)

Here―spin pseudo-vector, coordinates in the reference frame where a fermion has momentum. Vector has coordinates

(7)

in the fermion’s reference frame, where it is at rest.

Vector has the following coordinates in the reference frame in which the fermion has linear momentum

(8)

Spin tensor

(9)

has coordinates in the fermion’s reference frame:

(10)

Here―entirely anisymmertical tensor, , the same tensor. Note that

(11)

For the with a help of (5) and (6) we have:

(12)

This product contains 400 terms. The trace of most of them is zero. Calculations with the rest of the 164 terms lead to:

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

Here―dual to the tensor

(28)

The usual expression for the dot-product is used. Expression (13)-(27) determines the amplitude square for any quantum electrodynamics process with polarized particles. It has obviously Lo-

rentz’s covariant form. This expression helps to get rid of the time-consuming necessity of trace matrices products calculations for different processes. Results of such calculations are already included into (13)-(27). The only thing we need to do is to substitute specific coefficients I, , , , J for the interaction matrix M into (13)-(27). It is essentially reducing and simplifying calculations especially for the polarized particles. Expression (13)-(27) is very cumbersome. This is our price for its universality. Note that for the specific processes many of the quantities I, , , , J are zero so that only some fragments of the (13)-(27) are used. These fragments are marked by different numbers in (13)-(27). In each particular case expression (13)-(27) becomes

much simpler. As an example of such simplification let us use (13)-(27) for calculation of for an electron-muon collision.

3. Electron-Muon Collision

The electron-muon system transaction probability per unit time from the initial state to the final state can be calculated in the usual way:

(29)

Here―fine structure constant, V―normalization volume, which contains one electron and one muon,―final states density of the system with total energy and 3D impulse:

(30)

―solid angle, through the which electron is scattered. In (29)-(30) for electron (muon) quantities lower- case (upper-case) letters are used. Expression can be written as or, where or. Amplitude square can be obtained using only fragment

(15) from (13)-(27). The following quantities are zeroes, , ,. Then we need to contract tensor coefficient in front of the, calculated for the electron, with the similar tensor coefficient calculated for the muon. Note that the real parts of these coefficients are symmetrical tensors and the imaginary parts are anti-symmetrical tensors. That is why we must contract them separately and add the contraction results:

(31)

Expression (29)-(31) determines the transaction probability per unit time for the scattering of polarized electrons and muons. For the unpolarized particles one must average (31) by the initial polarizations of the particles and summing by the final polarizations of electrons and muons. It can be easily done in expression (31): all terms with, , , must be omitted and the result must be multiplied by 4 (2 for the electrons and 2 for the muons).

(32)

In the particular case when muon is at rest: further simplifications can be done. Namely, expression (32) becomes simpler:

Also expressions for the final states density of the system and quantity become simpler:

Thus, the scattering probability per unit time becomes:

(33)

Here―angle between and. Divide (33) by the electron beam density and obtain the well-known result―Mott cross-section [4] :

(34)

Here―classical electron radius. As we can see using expression (13)-(27) allows us to easily obtain process cross-section without a calculation of the trace of the matrix products.

4. Conclusion

The covariant form of the expression for the amplitude square for any interaction matrix is derived. The expression allows calculating cross-sections of any processes with polarized particles. In particular, the universal expression was used in order to calculate the transaction probability per unit time for the scattering of polarized electrons and muons. Then this result was averaged by the initial polarizations of the particles and summed by the final polarizations of electrons and muons. The final expression coincides with well-know expression for unpolarized particles (Mott cross-section).

Acknowledgements

The authors would like to thank Prof. Lukyanets S.P., Prof. Lev B.I., Prof. Tomchuk P.M. and Prof. Cooney for stimulating discussions. We also thank the Editor and the referee for their comments.

Cite this paper

KonstantinKarplyuk,OleksandrZhmudskyy, (2015) The Universal Expression for the Amplitude Square in Quantum Electrodynamics. Journal of Modern Physics,06,2219-2225. doi: 10.4236/jmp.2015.615226

References