Received 8 September 2015; accepted 18 October 2015; published 21 October 2015

ABSTRACT

The central part of the nuclear potential energy is shown to depend on the interacting masses of the nuclear matter. This mass dependent potential energy reduces to the usual Newtonian potential energy of the interacting masses when both the interacting masses are more than a certain limiting mass. This strong potential energy results when both the interacting masses are less than the limiting mass. The potential energy is applied to two more systems here and out of which one nucleus is in the middle of periodic table.

Keywords:

Newtonian Potential Energy, Mass Limit, Boron-5, Silver-95, Uncertainty Principle

1. Introduction

The gross properties of a nucleus are obtained by applying approximate potentials derived from quantum chromodynamics. In this note, a mass dependent potential energy is derived and it applies to any nucleus. It only depends how we choose the interacting masses of the given nucleus. Whenever the masses are quite large compared to the binding energy of the system, non-relativistic quantum mechanics can be used with any potential energy. For example, the electron and proton masses are very large compared to the binding energy of hydrogen atom and non-relativistic quantum mechanics provides a very good idea of the various properties of the hydrogen atom. The universal constant of gravitation is assumed to be universal for all values of the interacting masses. Once we relax this assumption for small masses like those of a nucleus, the results are stunningly accurate as shown in [1] -[5] . Usually, we generally assume that an interaction is constant to depend on the distance of separation between the interacting masses or charges. In [1] -[5] , the Potential energy is obtained assuming no dependence of the Universal Constant of Gravitation on the distance of separation between the interacting masses. Here, we overcome this deficiency and show how ar dependent G leads to the same potential energy that is used in the references cited. Moreover, the earlier application leads one to believe that this potential energy applies only to low mass number nuclei. To overcome this misunderstanding, we apply the potential energy to such a nucleus like silver isotope with a mass number 95.

What are the gross properties of a nucleus? 1) The binding energy, 2) the ground state wave function, 3) the total spin and 4) the principal energy levels. These are some properties with which we can decide the acceptability of the given potential energy. The mass dependent potential energy is presented in Section 2. In Section 3, the mass dependent potential energy is applied to two more nuclei. These results are in addition to our results that are presented in [1] -[5] with this potential energy. Section 4 contains our conclusions.

2. Mass Dependent Potential Energy

In general, the main nuclear potential energy consists of two parts. 1). The central part and 2) the Yukawa exchange factor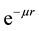. The Yukawa exchange factor limits the range of interaction. Let the central part of the nuclear potential be given by

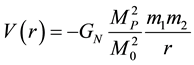. (2.1)

where, 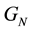is the universal constant of gravitation and,

. (2.2)

In order to account for various gross properties of nuclei such as Deuteron Helium-4 and many other nuclei, we were led to choose,

. (2.3)

The expression in Equation (2.1) looks different from the usual expression of Newtonian potential energy for interacting masses and. But Whenever,

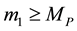and/or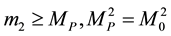. (2.4)

Equation (2.4) ensures that whenever even if one of the masses is greater than or equal to the cut-off mass 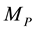the Newtonian potential energy is restored. For example, a neutron experiences the same acceleration as any other object near the earth because one of the masses (the earth) satisfies Equation (2.4). If and when both the masses satisfy the following condition, Equation (2.1) holds.

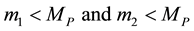. (2.5)

The same neutron experiences a different potential energy near a proton. It experiences the potential energy given by Equation (2.1) where for a proton-neutron there is no prior information as to the value of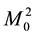.This parameter is specific to each pair of 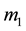and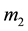. The parameter 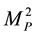is same for all interacting masses and provided they satisfy Equation (2.5). In plain words if a nucleus is envisaged or can be taken as two interacting masses and Equation (2.1) holds for its central part of the potential energy and is specific to the interacting masses. The potential energy is renormalizable. It is dimensionless when. In Ref. 5, we used it to explain the alpha decay of Beryllium-8 nucleus. It is only when Equation (2.4) holds we can relate to. Otherwise, it is a free parameter to be chosen by relating theory to experiment. The expression for the Potential energy given by (2.1) can also be arrived at in the following way.

Let the universal constant of gravitation G be a function of r where r is the distance between the interacting masses.

. (2.6)

where k is a dimensionless parameter and a has the dimensions of inverse length. The central part of the nuclear potential energy is given by,

. (2.7)

Suppose we choose k in the following way:

, (2.8)

where, f(N) is a function of the variable, such that,

whenever either, or/and. (2.9)

The above condition ensures that the factor k becomes equal to and the exponential factor inside the brackets in Equation (2.6) goes to zero irrespective of the value of r. On the other hand,

. (2.10)

If a system can be imagined to be made up of two interacting masses and which are both less than then the function f(N) is zero. In the case of any nucleus, the splitting of its masses can be arranged to satisfy this condition. So for any nucleus Equation (2.10) applies. In the product of even if one mass is more than or equal to then Equation (2.9) operates and thereby we recover the usual

Newtonian potential energy. From Equation (2.8), it is clear that k is dimensionless as the factor is a dimensionless positive real number. We observe that a in the exponential factor of Equation (2.7) must have the dimensions of inverse length. Let,

. (2.11)

The above factor is not a YUKAWA factor. In case of the Yukawa factor the mass appears as a single factor or as a sum but not as a product of masses. The factor a also indicates the dependence of on the product.We can use the r dependent G with the above definitions. To see what is really happening we can restrict r of the exponential of Equation (2.7) by means of the uncertainty principle. Let,

. (2.12)

That is specific to the product is also evident from Equation (2.12). The product. All the dependence of the gravitational constant on r is somehow now connected to. This is a specific approximation to arrive at the results we have already obtained in [1] -[5] . Inserting k, a and r into Equation (2.7), we note that,

. (2.13)

Assuming that f(N) = 0 for interacting nuclear masses or for those products of masses for which Equation (2.10) satisfies the above equation can be simplified to,

. (2.14)

From the above expression, it is quite clear why is given by Equation (2.2). Simplifying

Equation (2.14) we have,

. (2.15)

From Equation (2.15) it must be very clear that is same for all nuclei. In other words is same for all interacting nuclear matter. The factor has the dimensions of mass. It contains universal constants [see Equation (2.2)] and therefore it does not change with speed. The factor should likewise not change with speed of the interacting masses. The universal constant of gravitation can be modified by a choice of k and the product ar. For example, let and. For this case whenever f(N) satisfies Equation (2.10). That means that the universal constant is altered just numerically by a small number in this example. If this small change is effected in this way, the gravitational interaction plays no significant role whatsoever in the case of nuclear interaction. The point is that the choice of k through Equation (2.8) appears to relate the strong nuclear interaction to the Newtonian Potential Energy. The factor where b is a constant dependent on the product of the interacting rest masses and. The very fact that many gross properties of a nuclear system can be obtained through the application of the potential energy given by Equation (2.15), is an indication that the Morphed gravitational potential energy is indeed the right choice. The factor will be equal to 1, whenever Equation (2.4) or Equation (2.9) is satisfied. If where is as small as possible and tends to zero Equation (2.1) shows that the universal constant of gravitation is universal for all masses and gravitational interaction is ineffective in the nuclear context.

If the results of an experiment or observation match the theoretical prediction then there is good reason to accept the theory.

3. Applications

The potential energy in general should also include the YUKAWA factor to restrict the range of this interaction. For any nuclear interactions the potential energy is in general given by.

. (3.1)

The factor is specific to the choice of the product of the nuclear matter and this choice should follow the condition stipulated in Equation (2.10) or Equation (2.5). In Equation (3.1) the factor other than the YUKAWA Factor is what is called the morphed gravitational potential energy. In Equation (3.1), becomes equal to whenever Equation (2.4) or Equation (2.9) holds. In [4] , we applied Equation (3.1) to the scattering of a neutron by a nucleus and the theory explains the known experimental values. The morphed gravitational potential energy is earlier applied to many nuclei and all the results confirm the gross properties of these nuclei. In general, we have to solve the Schrodinger equation with the potential energy given by Equation (3.1). But the exact solution is not known for the full Yukawa potential energy given by Equation (3.1). Our results are almost correct because the morphed gravitational potential energy is tailored to suite the size of a nucleus through the uncertainty relation. Below we apply this potential energy to some more nuclei one of them is in the middle of the periodic table.

3.1. Boron-11

Boron nucleus contains 5 protons and 6 neutrons. The core for this nucleus consists of 5 neutrons and 5 protons. There is a neutron outside this core. The total spin of this nucleus in the ground state is. Hence, the outer neutron is in a state and therefore the principal quantum number for the ground state of this nucleus must be 2. The potential energy for this nucleus is given by,

, (3.2)

where, , and (3.3)

. (3.4)

The energy spectrum is given by,

. (3.5)

Here n = 2, 3, 4 is the principal quantum number as in the case of hydrogen atom.

The ground state (n = 2) energy for this nucleus is given by,

. (3.6)

The binding energy of this nucleus is 76.2046 MeV. The solution of the time independent Schrodinger equation led to the result given by Equation (3.5). By following

3.2. Silver

The Silver nucleus has many isotopes. One isotope of silver has a mass number of 95. This isotope is active most of the time. It has a total spin of. This indicates that this silver nucleus must have a core of 48 neutrons and 46 protons. The core mass is given by,

. (3.7)

There must be a proton outside this core of 48 neutrons and 46 protons with an orbital angular momentum quantum number of, for the ground state of this silver nucleus. The principal quantum number n must be 5 for the ground state of this isotope of silver. The total potential energy of this nucleus is given by,

, (3.8)

where is the fine structure constant in the second term above. Moreover.

. (3.9)

The mass defect for this nucleus is given by.

This is equivalent to a binding energy of 766.5079 MeV. With the potential energy given by Equation (3.8) the time independent Schrodinger Equation can be solved as in Refs. (1,2,3). The energy eigen-values are given by,

, (3.10)

where, (3.11)

In Equation (3.10), is the reduced mass. Non-relativistic quantum mechnics still holds because the masses of the interacting particles, proton and the core part have more mass than the binding energy of the system. For example in the case of hydrogen atom the binding energy is very small compared to the masses of the proton and electron. From Equation (3.10) we note that,

. (3.12)

When n = 5, the ground state energy is −766.508 Mev. The binding energy of this nucleus is 766.5 MeV. To decide whether a neutron or proton is outside the core we have to examine the magnetic moment of the silver-95 nucleus.

4. Conclusions

In this note, the Newtonian potential energy is modified through a limiting mass. A system like a nucleus can be imagined to consist of two interacting parts with their masses interacting through a potential energy similar to the gravitational potential energy. The mass parameter is an unknown parameter and it depends on the product of the masses. In all the examples we have considered so far, is different for different Nuclei [1] -[5] . It has a far reaching consequence. The principle of equivalence is not necessarily valid for interacting masses below.Whenever the interacting masses satisfy Equation (2.5) or Equation (2.10), the universal constant of gravitation is not universal.

In general, we should use Equation (3.1) for any nucleus. Here, we use it without the Yukawa factor to explain the gross properties of silver nucleus which is in the middle of the periodic table and has 95 nucleons. Is it possible to explain these results for this nucleus through QCD?

Acknowledgements

The author is very grateful to Prudhvi RChintalapati.

Cite this paper

Cvavb ChandraRaju, (2015) Strong Interaction and Newtonian Potential Energy. Journal of Modern Physics,06,1814-1819. doi: 10.4236/jmp.2015.613185

References