Received 29 May 2015; accepted 19 July 2015; published 22 July 2015

ABSTRACT

A theory of gravitation in flat space-time is applied to homogeneous, isotropic cosmological models. There are non-singular cosmological models. A natural interpretation is a non-expanding universe. The redshift is an intrinsic effect and not a Doppler effect. The universe contains only energy in the beginning, i.e. no matter exists. In the course of time matter and radiation are created from energy where the whole energy is conserved. Matter increases with time but a certain time after the beginning of the universe the creation of matter is finished and the universe appears like a static one. A modified Hubble law is considered which may explain the high redshifts of objects in the universe without the assumption of dark energy.

Keywords:

Universe, Non-Expanding, Non-Singular, Creation of Matter, Conservation of Total Energy, Redshift Is No Doppler Effect, Modified Hubble Law

1. Introduction

Einstein’s general theory of relativity yields a singularity in the beginning of a homogeneous, isotropic universe. Hence, space and time do not exist before and are created in the beginning. The redshift is interpreted as Doppler effect which yields the expansion of space. This is the mainstream interpretation of cosmological models studied by general relativity. It is implied by the singularity of the models.

A theory of gravitation in flat space-time is studied by the author in several articles, e.g. in article [1] and in the book [2] . The theory of gravitation has a flat space-time metric. Gravitation is described by gravitational potentials which form a tensor of rank two. The source of these potentials is the total energy-momentum tensor including that of the gravitational field which is a tensor by this theory. This theory is a field theory in analogy to the well-known Maxwell’s electrodynamics. For weak gravitational fields the results of this theory agree with those of general relativity to measurable accuracy. In the beginning of the universe where strong gravitational fields work there are differences between the results of the two theories.

In the beginning of the universe only energy exists, i.e. there is no matter. In the curse of time matter and radiation are created at coasts of energy where the total energy is conserved. Non-singular cosmological models exist, i.e. a big bang doesn’t exist. The creation of matter is finished a certain time after the beginning of the universe, i.e. the creation of the universe is finished. It is now like a stationary universe. A natural interpretation is a non-stationary, non-expanding universe, the creation of which is finished. The redshift is an intrinsic gravitational effect and not a Doppler effect. A non-expanding universe is also experimentally indicated by several authors, e.g. the articles [3] - [8] . Theoretical studies of a non-expanding universe are given by several authors (see e.g. [9] - [14] ). A fast increase of the inhomogeneity in the matter dominated universe by flat space-time theory of gravitation is given in article [15] . This is important to explain the presently observed inhomogeneity in the universe. General relativity gives only slow increase of the inhomogeneity which does not allow to explain the presently observed universe.

Chapter 2 contains the theory of gravitation in flat space-time which is a field theory. The metric is a flat space-time, e.g. the pseudo-Euclidean metric. The gravitational field satisfies covariant differential equations of order two with the total energy-momentum as source. Conservation of the total energy-momentum and the equations of motion for matter are stated (see e.g. article [1] and the book [2] ).

In Chapter 3 a homogeneous, isotropic universe is studied. The pseudo-Euclidean metric is used implying a flat space as indicated by measurements. The matter consists of dust and radiation. The universe is described by two functions. There is no singularity, i.e. no big bang. The absolute time is introduced. There is no age problem. A redshift formula is derived.

A modified Hubble law is described in Chapter 4 by the assumption that everybody is surrounded by a medium similar to that in electrodynamics. Absolute time is used and a modified Hubble law is derived. Quasars and galaxies with nearly the same redshift can have quite different distances as already experimentally indicated by Arp. Redshifts can give smaller distances of the objects than by the standard Hubble law. It may be that dark energy in the universe is not needed because the high redshifts are explained by the modified Hubble law.

The theory of gravitation in flat space-time and the general theory of relativity are compared with one another from the theoretical point of view in article [16] . A modified Hubble law is stated in article [17] which may be important to explain the high redshift of quasars without the assumption of dark energy. The existence of nearby quasars and galaxies with quite different redshifts is already stated by Arp [18] . This is also in agreement with the modified Hubble law in article [17] . Results about a non-singular, non-expanding universe can also be found in the book [2] .

2. Gravitation in Flat Space-Time

A theory of gravitation in flat space-time is studied in several articles ( see e.g. article [1] and the book [2] ) gives for small gravitational fields the same results as general relativity to measurable accuracy. In this section the theory is shortly summarized.

Let 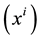be the coordinates of space-time and 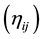the symmetric metric tensor of flat space-time with line-element

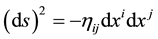. (3.1)

A special case is the pseudo-Euclidean geometry where 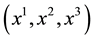are the Cartesian coordinates, and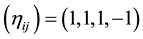. The gravitational field is described by a symmetric tensor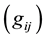. The proper-time is defined by

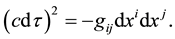(3.2)

Put

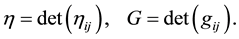
Define the tensor 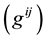by

.

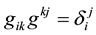Then, the Lagrangian for the gravitational potentials is defined by

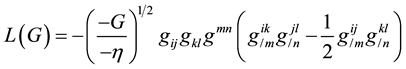(3.3)

where the bar/denotes the covariant derivative relative to the metric (3.1). Let k be the gravitational constant and put

.

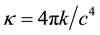Then, the energy-momentum 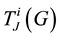of the gravitational field from the Lagrangian is

(3.4)

This is a tensor whereas the energy-momentum of general relativity is not a tensor.

The energy-momentum tensor of matter is

(3.5)

Here, and denote the density, the pressure and the four-velocity of matter. It holds by relation (3.2)

(3.6)

Define the differential operator of order two

. (3.7)

Then, the field equations for the potentials from the Lagrangian (3.3) are

(3.8)

where is the total energy-momentum tensor of matter and of the gravitational field, i.e.

(3.9)

The equations of motion are

(3.10)

where

(3.11)

is the symmetric energy-momentum tensor of matter. In addition to the field Equations (3.8) we have the conservation of the total energy-momentum tensor, i.e.

(3.12)

The field Equations (3.8) and the equations of motion (3.10) imply the conservation law (3.12) of the total energy-momentum. In addition, the field Equations (3.8) and the conservation law (3.12) of the total energy- momentum give the equations of motion (3.10).

The field Equations (3.8) are formally similar to those of general relativity with quite different meanings of and.

The theory of gravitation in flat space-time and that of general relativity are compared with one another from the theoretical point of view in article [16] .

3. Homogeneous, Isotropic Universe

Flat space-time theory of gravitation is applied to a homogeneous, isotropic universe. The results can be found in several articles, especially in [11] and in the book [2] .

The metric is the pseudo-Euclidean geometry, i.e.

(4.1)

The potentials are

(4.2)

which implies the proper-time

(4.3)

Assume that matter is at rest, i.e.

which gives by (3.2) the four-velocity

The matter tensor has the form

(4.4)

Here, and are the densities of matter and radiation and is the pressure of radiation, i.e.

(4.5a)

The pressure of matter is that of dust, i.e.

(4.5b)

The energy-momentum tensor of gravitation is given by

(4.6)

with

(4.7)

The prime denotes the time-derivative.

The equations for the gravitational field have the form

(4.8a)

(4.8b)

The conservation of the total energy gives

(4.9)

where is a constant of integration. The equations of motion imply under the assumption that matter and radiation do not interact with one another:

(4.10)

where and are the present densities at time.

The initial conditions for the differential Equations (4.8) are the values at present time:

(4.11)

where Is the Hubble constant and is a further constant which is zero for general relativity.

Let and be the well-known density parameters of radiation and matter. Put

(4.12a)

and

(4.12b)

The it follows from (4.9) for

(4.13)

Longer calculations imply the relations

(4.14b)

(4.14b)

The condition

gives by the use of (4.12b) that the denominator of (4.14b) is positive for all. Hence, non-singular solutions exist. Let us assume

(4.15)

then, there exists a time

(4.16)

and for all holds

We get for

(4.17a)

(4.17b)

Put

(4.18a)

and assume

(4.18b)

then, the solutions are approximated by

(4.19a)

(4.19b)

In the beginning of the universe, i.e., the functions are

(4.20a)

(4.20b)

This means that the universe starts with a small positive value at and decreases till with. Then, it increases to infinity as. The function is infinite at and it is always decreases for all to a value a little bit smaller than 1. In the beginning of the universe there is no matter and no radiation. In the course of time matter and radiation are created. A certain time after the beginning of the universe the creation of matter is finished, i.e. the total universe is created. Hence, the universe appears as a static one. A static universe is also claimed by Watts [5] .

In addition to the time t there exist the proper time defined by

(4.21a)

and the absolute time defined by

(4.21b)

The proper time is measured by atomic clocks. The introduction of the absolute time gives

(4.22)

i.e. the light-velocity in the universe is at every time equal to the vacuum light-velocity c.

The universe happens in the pseudo-Euclidean geometry with the time transformation (4.21b). Hence, space is not expanding.

Two light rays are emitted at distance r at time resp. and they are received at at time 0 and. Hence, it follows

The last two relation yield

(4.23)

Therefore, the time-intervals are at any time always identical.

The Equation (4.14b) is by the use of (4.14a) and the use of the absolute time of (4.21b) rewritten the form

(4.24)

The frequency of an atom emitted at time in the universe is by (4.22)

(4.25)

where is the emitted frequency of the same atom at present time. By the use of (4.22) the change of the photon-energy during the motion of the photon in the universe is given by

Hence the frequency (energy) is not changed when light moves in the universe. Therefore, the measured redshift at the observer at present time is

(4.26)

The redshift formula (4.26) implies by the use of (4.24), differentiation of (4.24) and the constant velocity of light c in the universe

(4.27)

The age of the universe measured with absolute time from time till the present time is by the use of (4.24), (4.13), (4.15) and (4.16)

(4.28a)

The age of the universe from the beginning till is by the use of (4.24), (4.16) and (4.20a)

(4.28b)

Hence, the age of the universe measured with absolute time from the beginning till is very small compared to the total age of the universe.

There is no age problem for the universe by the use of the absolute time which is more natural than the proper time by virtue of the constancy of the light-velocity c in the universe.

There exist several articles which require a universe with non-expanding space (see e.g. [3] - [10] [12] ). Non- singular universes are studied in the articles [11] - [14] .

A theoretical comparison of the theory of gravitation in flat space-time with general relativity is given in the article [16] . The total energy-momentum tensor of matter and gravitation is the source of the gravitational potentials whereas general relativity has only the energy-momentum of matter as source since the energy-mo- mentum of gravitation is not a tensor. Therefore, the Ricci tenor is used to describe the gravitational metric which implies non-Euclidean geometries. Experimental results indicate that the space of our universe is flat in agreement with flat space-time theory of gravitation. A flat space yields difficulties to be explained by general relativity since in the beginning of the universe there is a high matter density which implies high curvature. Therefore, the inflationary universe is introduced.

It is worth to mention that flat space-time theory of gravitation gives in the matter dominated universe a fast increase of the inhomogeneity of matter (see [15] ). This is necessary to explain the observed inhomogeneity by galaxies and quasars. General relativity has difficulties to explain this inhomogeneity because only weak increases can arise.

4. Modified Hubble Law

The interpretation of an expanding space gives with recently observed high redshift quasars an acceleration of the expansion of the space. This is partly explained by the introduction of a cosmological constant in the general theory of relativity. This is also possible for flat space-time theory of gravitation.

Here we will consider another possibility. Let us assume that a body is surrounded by a medium analogous to that of electrodynamics with electric permittivity and magnetic permeability. We put

(5.1)

We follow along the lines of article [17] and that of the book [2] . Put

(5.2)

with

(5.3)

Then, the proper-time is given by

(5.4)

Let be the electric four-current density and consider the covariant differential equations

(5.5a)

. (5.5b)

The electric and the magnetic field are defined by

(5.6a)

and the derived fields are

(5.6b)

Then, it follows from (5.5) with (5.2) and (5.3)

(5.7)

and with the abbreviation we have the well-known Maxwell equations in a medium

(5.8a)

(5.8b)

Let us now consider a medium in the universe described by the absolute time and. We define the approximating potentials

(5.9)

The metric is given by

(5.10a)

and the proper-time has the form

(5.10b)

Assume that an atom at rest emits a light ray at time in the universe. The Equation (5.10b) gives for the proper-time

(5.11)

Hence, the emitted frequency is

(5.12)

Assume that the light-ray moves only a small part of his way to the observer in this medium. In the exterior of the medium relation (4.22) holds, i.e. the frequency is not changed during the motion. Hence, the redshift at the observer is

(5.13)

which gives analogous to Section 4

(5.14)

Hence, we get an intrinsic redshift by the medium, i.e. the standard Hubble law doesn’t give a real distance indicator. We must use the modified Hubble law (5.14).

We can assume

(5.15)

Then, we conclude:

(1) The linear modified Hubble law overestimates the Hubble constant.

(2) For a fixed redshift the resulting distance of the object is smaller than by the standard Hubble law.

(3) Quasars and galaxies with nearly the same distance can have quite different redshifts depending on the medium in which light is emitted (see e.g. Arp [18] ).

(4) Quasars may be nearer than by the standard Hubble law. Hence, the measured energy emitted from these quasars is smaller than generally assumed.

(5) It is possible that the assumption of dark energy in the universe is not necessary because the higher redshift implying the acceleration of the universe may be explained by the surrounding medium of the objects, as e.g. of galaxies and quasars.

All these results can be found in the article [17] and in the book [2] .

5. Conclusion

The theory of gravitation in flat space-time gives a non-expanding, non-singular universe, i.e. there exists no big bang. The redshift is an intrinsic effect and not a Doppler effect. Space is not expanding. In the beginning of the universe only energy exists and no matter. In the course of time matter (dust) and radiation are created whereas the total energy is conserved. Matter increases with time and a certain time after the beginning the creation of matter is finished, i.e. the total universe appears static. A modified Hubble law is given which may explain the high redshifts of objects in the universe without the assumption of dark energy.

Cite this paper

WalterPetry, (2015) Creation of a Non-Expanding, Non-Singular Universe. Journal of Modern Physics,06,1085-1094. doi: 10.4236/jmp.2015.68113

References