Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57375,5 pages
10.4236/jmp.2015.67096
A Fresh View for Maxwell’s Equations and Electromagnetic Wave Propagation
Narahari V. Joshi
Department of Physics, University of Los Andes, Merida, Venezuela
Email: joshi@ula.ve
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 20 June 2015; published 24 June 2015
ABSTRACT
Equations related with wave propagation are reexamined as in certain circumstances law of conservation of energy is not fulfilled even though it is cautiously clarified with the help of Heisenberg’s uncertainty principle. Recently, attempt has also been made to understand certain discrepancies in optical phenomena like diffraction or interference. The purpose of the present investigation, therefore, is to overcome some discrepancies by introducing constants of integration in Maxwell’s Equation. It turns out that the presence of vibrating strings (or store energy) in the medium becomes essential to understand several details of the wave propagation.
Keywords:
Maxwell’s Equations, Wave Propagations, String Theory

1. Introduction
A set of Maxwell Equations [1] is fundamental in electricity and magnetism and they are developed on the basis of numerous experimental data. Almost all the theoretical work is based directly or indirectly on this set of equation together with the equation related with Lorentz force. Transformers, inductors, and many types of electrical motors and generators are based on these principles. Even more, a significant property of these equations is that they give rise to the wave equation for electric and magnetic fields denoted by E and B respectively. In spite of the importance of this set of equations, the proper attention for the origin and the basic mechanism behind these principles has not received due attention. Recently, some aspects of Lorentz force [2] and Faradays law [3] are evaluated on the basis of the presence of strings in the form of a compact liquid by Joshi. It turns out that fluid dynamics explains several aspects of Maxwell’s Equation as mentioned earlier [4] . The purpose of the present investigation, therefore, is to examine details of these equations related with electromagnetic wave propagation and the variation of the electric field (E) with respect to the magnetic field (B) in free space.
2. Theoretical Developments
It is known that wave equations are obtained from Faraday law and they are given by [1]
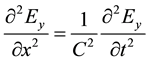 (1a)
(1a)
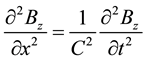 (1b)
(1b)
Here Ey and Bz are the strengths of electric and magnetic fields in Y and Z directions respectively.
The stander solution for this equation is generally given by
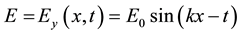 (2a)
(2a)
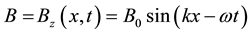 (2b)
(2b)
where 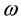 is the angular frequency of the oscillation,
is the angular frequency of the oscillation, 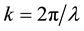 and
and  is the wavelength.
is the wavelength.
In this solution of the wave equation (or these types of equations) the constant of integration is always neglected or considered as 0 and the wave propagation is explained perfectly. However, if constants of integration are added then the solution of Equation (1a) can be expressed as
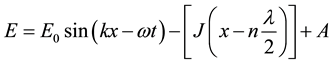 (3)
(3)
Here n is a positive integer.
In fact, the introduction of constants, term  and A do not affect or alter the second order partial differential equations, but, are necessary to examine them. Contribution from
and A do not affect or alter the second order partial differential equations, but, are necessary to examine them. Contribution from 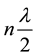 takes into account the
takes into account the
periodicity of the motion and its importance will be discussed later. These constants which will make a substantial difference and their consequences will be evaluated in the present investigation.
At the start, when x and n both are 0, the electromagnetic energy has a constant value given by A. It suggests that the medium through which the wave is propagating has energy which is in agreement with the string theory, according to it the space is filled with vibrating strings [4] . Moreover, several experimental data confirm that vacuum has energy and even it can be converted into electromagnetic energy [5] . Some patients have been already registered to convert space energy into electrical energy for application purpose [6] .
Recently, it has been noted that several electromagnetic phenomena have been explained on the basis of strings as a compact, non viscous, surface tension free liquid [2] - [4] . From the point of view of quantum field theory, this forms a system of coupled harmonic oscillators and obviously the oscillatory motion is not limited to a single oscillator but it forms a collective oscillating system of vibrating strings. A coupled oscillating system forms a vibrating line of strings [7] . It has been found out that there is a little difference between continuous and discrete line. Smaller the dimension of the vibrating elements, the difference between continuous and discrete nature is reduced considerably. Moreover, the system has another advantage namely that it is a flexible. The details of the strings from the point of view of vibrational properties are not known and consequently, there does not exist a precise formalism to estimate the vibrational properties of the system and hence the constant,
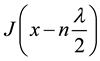 needs to be introduced to understand the basic mechanism of the collective system. The negative sign is assigned to
needs to be introduced to understand the basic mechanism of the collective system. The negative sign is assigned to 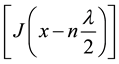 so that it represents the force constant corresponding to harmonic oscillator or for a system of coupled oscillators. Moreover, the term
so that it represents the force constant corresponding to harmonic oscillator or for a system of coupled oscillators. Moreover, the term 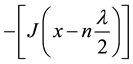 indicates that every pulse of the
indicates that every pulse of the
wave contributes in the activation of the harmonic oscillator. The variation of the electromagnetic field in x direction directly creates the compression of the system of strings. Therefore, J represents the restoring force constant for the corresponding displacement. According to quantum field theory, a close association of fields and
harmonic oscillations is well established. This is the reason why the term  has been introduced as
has been introduced as
a constant of integration. It is worth mentioning that Equation (3) satisfies the wave equation given by Equation (1a).
The other important reason is that the field quantization is based on the assumption that there exists a discrete field quantum and therefore each field is connected to a discrete quantum oscillator. Quantum features of the fields are extensively discussed earlier and it is established that it can be expressed in the form of harmonic oscillator. Hamiltonian for harmonic oscillator is given by [7] [8]
 (4)
(4)
which is used for formalism of quantum field theory for electromagnetic fields.
Here q is a generalized co ordinate and p is the momentum operator given by [7] [8]
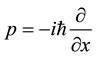 (5)
(5)
It is known that the non interacting Hamiltonian of electromagnetic fields participates in the creation and annihilation of particles, the corresponding operators a+ and a are given by [7] [8]
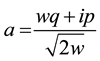
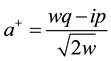
In this case, Hamiltonian for harmonic oscillator turns out to be [7] [8]

Here 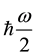
Creation and annihilation of particles are also examined from the point of view of increase or decrease of the excited states of the harmonic oscillator. Therefore, it is necessary to introduce the presence of oscillators in the system. Moreover, it is found that in the wave propagation process [7] , the conversion of fields into particles (or vice versa) is necessary to conserve the total energy of the system [8] . Therefore, the constant J, related with the creation-annihilation process, has been introduced in Equation (3)
3. Relation between Electric and Magnetic Field
Now, let us consider electromagnetic wave motion where the variation of electric field is in x direction and apply Faradays law, namely
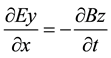
By using Equations (8) and (3), we get

as ω/k is the velocity of light C, then the Equation (9) becomes
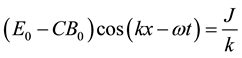
Here, k is the wave vector indicating that the direction of the photon flux coincides with the direction of the propagation of the wave. Equation (10) is very significant and it differs from the conventional as it includes an extra term which incorporates J corresponding to the creation annihilation of particles; thus fields and particle approach are taken into account. If this aspect is neglected, and if it is accept that J = 0, then only the Equation (9) takes the conventional form

An additional term is necessary to balance the equation as E is directly proportional to B. Electric and magnetic fields are increasing (or decreasing) simultaneously without having the mechanism for adjusting the conservation of energy. Instead of providing a suitable explanation, this observed phenomenon is justified (not rigorously) with the help of Heisenberg’s uncertainty principle. This aspect has been already brought to notice by Joshi [8] [9] . According to the quantum field theory, free non interacting Hamiltonian of the field plays the role in the creation and the annihilation of the particle. Therefore, the insertion of integration constant J is necessary. Thus, at every point is space and time the sum of energies associated with electric, magnetic fields and photons (created or annihilated) are conserved in the radiation propagation process.
Now let us examine the Equation (10) which indicates the motion of the flow of the energy of the electro-
magnetic fields. As mentioned earlier the term 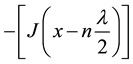
oscillator in one dimension originated from the vibrating string. As J is a restoring force constant, the total energy, U, or Hamiltonian of the harmonic oscillator corresponding to the vibrating string system is given by
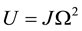
where and 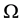

and hence
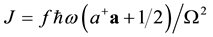
Therefore, Equation (10) can be written as
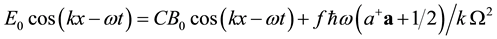
The Equation (15) clearly indicates that as the electric field increases, the magnetic field also increases but the energy is conserved by the annihilation process which is expressed with the second term. Similarly, when electric and magnetic fields start decreasing, the particles are created and their density becomes maximum when electric field becomes zero. It also takes into account the possibility of energy storage in the form of increasing excited state of the oscillator. Thus, the energy is conserved in the process and when the pulse passes it is stored and reused for the generation and the flow of the next pulse of electromagnetic field.
Now, the solution of wave Equation (3) becomes
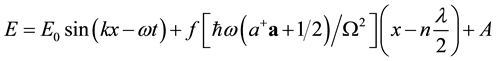
The second term contributes in the annihilation or creation of the particles and free (non interacting) Hamiltonian is a determining factor for this process. The term A corresponds to the buffer energy of the vibrating system. Thus the medium through which the wave is propagating is excitable, continuous and it can also be used as a source of buffer energy, it means it can be stored and reused. In such a system, the flow of energy is easy to understand. It means that when the electric field (or magnetic field) is oscillating, the total energy of the system is conserved without applying Heisenberg principle of uncertainty.
It is worth mentioning that Equation (11) is derived from Equation (8) which is based on Faradays law. Recently, the origin for this important law has been examined on the basis of the presence of strings and it has been concluded that a medium is required for converting the variation of magnetic field into electric field. This view also supports the approach presented here.
In short, the insertion of two constants namely J and A in well accepted solution of wave equation suggests that there must be an excitable medium through which the electromagnetic wave propagates and the mechanism of conversion of free field into particles (vice versa) based on quantum field theory helps to conserve the energy during the entire processes. This supports the presence of vibrating elements in the space. It is worth mentioning that all aspects of string theory are not considered here; but it is only assumed the presence of vibrating elements.
4. Discussion
The above approach clearly indicates that when the electric field (or magnetic field) is maximum, the free Hamiltonian is zero and hence the rate of particles creation is zero. Meanwhile, when the intensity of the electric field starts decreasing, the operators start creating particles. From the point of view of quantum field theory, the creation operator raises the energy level of an Eigen state of harmonic oscillator or they are getting excited. When the electric field is zero (at nλ/2,) the density of the particles created by the operators is maximum and the harmonic oscillator is de-excited converting the energy into photons. Thus, Huygens wave front is formed and the process of propagation is continued.
This point of view is in agreement with an earlier work where some discrepancies have been reported about the propagation of electromagnetic waves with the help of Huygens wave front. Moreover, a different approach for diffraction phenomenon has been suggested where the separation between two wave fronts is not infinitesimally small but it is found to be λ/2 where the density of photons or particles is maximum. This has explained the observed diffraction pattern successfully for circular aperture without ad hoc assumptions [9] and can be generalized to similar interference and diffraction patterns.
The other important aspect is that the present approach also helps to understand the wave motion when it is expressed in a spherical polar coordinate system. The solution of the wave equation in polar coordinates is given by [10]

where K is a constant corresponding to the intensity of the electric field.
According to Equation (17), when r = 0, the amplitude becomes infinite and the wave propagation at the origin cannot be explained. This difficulty has been overcome with the present view as at time t = 0, the propagation starts with the particle nature of the radiation [10] . The details of the dual nature of the radiation and its validity during the propagation of the wave have been pointed out earlier. The new point of view presented here explains several optical phenomena like diffraction, the role of Huygens wave front, Kirchhoff’s correction factor etc. satisfactorily [9] . The foundation given in this paper and earlier publications support the inference expressed by Einstein indicating that radiation does not only propagate in the form of wave but it is self trapped giving origin to the quanta [11] .
5. Conclusion
In the present investigation, wave equations are reexamined by introducing the constants of integration. It is noted that equation E = BC needs an additional term to balance the energy. Moreover, the presence of the constants strongly suggests that wave propagation needs an excitable, continuous medium where the energy can be stored and reused. The situation is explained with the help of the system of vibrating strings in the form of compact liquid.
References
- Feynman, R.P., Leighton, R.B.M. and Sands, M. (1969) The Feynman Lectures on Physics. Addition Wesley, Boston.
- Joshi, N.V. (2014) World Journal of Mechanics, 4, 247-250.
- Joshi, N.V. (2014) World Journal of Mechanics, 4, 309-314.
- Joshi, N.V. (2013) Physics Essays, 36, 61-67. http://dx.doi.org/10.4006/0836-1398-26.1.61
- Bearden, T.E. (2004) Energy from the Vacuum. Cheniere Press, Santa Barbara.
- Haisch, B. and Moddel, G. (2008) Quantum Vacuum Energy Extraction. USA Patent No. 7379286.
- Henley, E.M. and Thirring, W. (1962) Elementary Quantum Field Theory. McGraw-Hill, London.
- Joshi, N.V. (2010) Comments on the Dual Nature of Photons. Quantum Optics SPIE Proceeding, Vol. 7727.
- Joshi, N.V. (2013) Optik, 124, 6122-6123. http://dx.doi.org/10.1016/j.ijleo.2013.04.084
- Joshi, N.V. (2012) Journal of Optical Communication, 33, 57-59.
- Einstein, A. (1917) Physikalische Zeitschroft, 18, 121-125.

