Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53439,11 pages
10.4236/jmp.2015.61008
Constitutive Elements of Non-Abelian Gauge Theories
Ademir E. Santana1, Samuel Simon2
1International Center for Condensed Matter Physics, Instituto de Fisica, Universidade de Brasilia, Brasilia, Brazil
2Deaprtamento de Filosofia, Universidade de Brasilia, Brasilia, Brazil
Email: a.berti.santana@gmail.com, samuell@unb.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2014; accepted 19 January 2015; published 22 January 2015
ABSTRACT
A set, S, of constitutive elements characterizing mechanical theories is defined. In S, the role played by concepts such as mass, particle, fields and symmetry is discussed. This structure is first used to consider the Nöther’s theorem from an algebraic point of view. As examples, we explore non-relativistic quantum mechanics and special relativistic particles. The set S is then applied to analyze non-abelian gauge theories, considering the Higgs mechanism for generation of mass.
Keywords:
Gauge Fields, Constitutive Elements, Lie Symmetry

1. Introduction
With the emergence of subatomic theories, in the 1920s, the problem of establishing the basis of quantum mechanics, considering the classical mechanics counterpart, came about [1] [2] . Attempts to address this pro- blem gave rise, over the decades, to numerous works, following different mathematical approaches and physical motivations. Although much of these investigations have been initially restricted to the analysis of classical and quantum premises in the non-relativistic realm, they have led to important discoveries, such as the notion of entanglement and teleportation, crucial keys for quantum computers and quantum network [3] - [5] ; concepts that have been explored in high energy physics [6] . These investigations are mainly considered in two directions, that are at some extent complementary to each other.
One of them is the stochastic methods, that have been used to derive quantum mechanics starting, for instance, from the Liouville equation or from the Fokker-Planck equation [7] - [15] . In another direction, there are attempts exploring the notion of symmetry and representation theories [16] - [20] . The former direction usually em- phasizes the nature of the state, being interesting for deriving, for example, the Schrödinger equation, while the later, guided by algebraic structures and symmetries, is useful for generalizations, and can accommodate an abroad class of mechanical systems, that include relativistic, non-relativistic and thermal systems [21] [22] .
For the case of non-relativistic quantum mechanics, Levi-Leblond [23] - [25] was the first to present a systematic study of unitary representations of the Galilei group, leading to the Schrödinger equation and Pauli- Schrödinger equation, describing, respectively, spin-0 and spin 1/2 non-relativistic particles. A consequence, in terms of premises, was that the spin of a particle should be fully described and physically interpreted in terms of the rotation symmetry. It is important to note that, before these works, it was usual to consider spin in the non- relativistic quantum mechanics as a relativistic remnant of the Dirac equation.
Although representations of Lie group are key aspects to deriving physical theories, this method, as well as the stochastic analysis, has been only partially explored to address the premises of quantum field theories in comparison with other mechanical theories [6] [15] [18] [26] . This is a demanding problem, since new phenomena and concepts need to be analyzed in detail. The situation is more appealing in non-abelian gauge field theories, as the standard model for particle physics, where the nature of the mechanism for the origin of mass is only partially explained through the introduction of the Higgs bosons, presently under experimental test.
In the present work, our main goal is to construct a systematization for mechanical formalisms, which is established by six constitutive elements. In this context, gauge fields are considered by taking into account counterparts of other theories of motion, such as quantum mechanics and one-particle special relativity. The general algebraic structure is supported by physical (experimental) conditions. A first result is a derivation of a Lie-al- gebra structure associated to the six constitutive elements. This aspect, which is in turn connected to the Nöther theorem, is important to establish the consistency of the number of six constitutive elements. After analyzing the structure of quantum mechanics and special relativity, we investigate non-abelian fields, discussing the concept of mass, from Newton up to Higgs. We have to emphasize that what is new in the present work is the structure of six constitutive elements fixing the content of theories of motion. This aspect is useful, as aforementioned, for the comparative analysis of theories. In this realm, for instance, a fundamental difference between classical and quantum mechanics is not the nature of the Hilbert space, but the experimental condition imposed by the Heisemberg relations.
The paper is organized in the following way. In Section 2, we present the constitutive elements of a mechanics. In Section 3, there is a demonstration that the constitutive elements induce an algebraic structure of Lie algebra in association with the Nöther theorem. In Section 4, the premisses of the special relativity theory and quantum mechanics are analyzed. In Section 5, non-abelian gauge theory is discussed as a mechanical theory. In Section 6, the notion of mass is analyzed. The final concluding remarks are presented in Section 7. In the Appendix, we review some well know aspects of gauge theories in order to make clear the origin of the six constitutive elements.
2. Constitutive Elements for Theories of Motion
A theory of movement, a mechanics, can be defined by the following set, 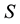 , of constitutive elements (CE).
, of constitutive elements (CE).
CE1. Reference systems. A reference system is defined from points in the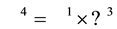 , where
, where  stands for the time and
stands for the time and  is the Euclidian space. Time is defined by clocks and the Euclidian space is defined by the constructions of rods. In both the cases, the definitions are given by considering events relative to each other. The mechanical characterizations of the manifold
is the Euclidian space. Time is defined by clocks and the Euclidian space is defined by the constructions of rods. In both the cases, the definitions are given by considering events relative to each other. The mechanical characterizations of the manifold 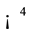 is specified by the kinematical symmetry of the space time. Since a general symmetry is a continuous mapping
is specified by the kinematical symmetry of the space time. Since a general symmetry is a continuous mapping ,
, 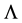 can be taken as a Lie-group (see next section for a general explanation). It is important to mention that a clock is defined by any periodic system, such that this periodicity depends on the experimental precision.
can be taken as a Lie-group (see next section for a general explanation). It is important to mention that a clock is defined by any periodic system, such that this periodicity depends on the experimental precision.
CE2. Kinematical variables. The set of kinematical variables, 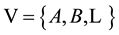 , is defined as an associative algebra, such that each element of
, is defined as an associative algebra, such that each element of 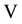 is in correspondence with aspects of motion taking place in
is in correspondence with aspects of motion taking place in . There is a subset
. There is a subset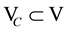 ,
,  from which all the elements of
from which all the elements of  are constructed in the form
are constructed in the form
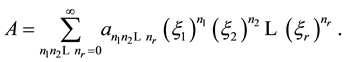
The set 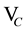 will be called the set of canonical variables.
will be called the set of canonical variables.
CE3. Mechanical system. A mechanical system is defined as the object under movement. It can be classified by two categories of primitive concepts. One is the material point, specified by a set of local points of 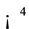 and endowed with the content of momentum. The other is the concept of a field, which is a mechanical system with no local characteristics in
and endowed with the content of momentum. The other is the concept of a field, which is a mechanical system with no local characteristics in 
CE4. State of a mechanical system. The mechanical state 





CE5. Changes in the state of mechanical system. The changes in the state 

















CE6. Specification of mechanical systems. The specification of a particular mechanical system is given by a function of the state of the system, 



The equations of motion, the causal law, will be the Euler-Lagrange equations and are given by the functional equation
3. Lie-Algebra Structure of Ω and Nöther’s Theorem
In this section, using physical (experimental) ingredients of the motion, we show that the set of transformations 










For simplicity, we consider that each element of 




that is, the mapping (,) is antisymmetric.
Since 













which is the derivation of the Leibnitz rule, defining the association between the associative product 

Let 




considering now that 


which is the Jacobi identity. Then the mapping 

From these results, we observe that an invariant quantity, say



4. Two Examples: Special Relativity and Quantum Mechanics
In this section we investigate the constitutive elements of mechanical system with two examples: one particle special relativistic system and one particle quantum mechanics.
4.1. Special Relativity
The constitutive elements of a particle in special relativity are identified in the following way.
CE1. Reference systems. The reference systems is defined from points in the













CE2. Kinematical variables. The set of kinematical variables, 






CE3. The mechanical system. We consider as a mechanical system a material point. The mass of material point is defined with the characteristics of a Newtonian material point with inertia, but now mass, 



CE4. The state characterizing a material point can be given by











CE5. Changes in the state of mechanical system. The changes in the state given by 

CE6. The specification of the particular mechanical system is given by a function of the state of the system, 




It is important to consider now another representation for relativistic particles, the Poisson-Liouville formul- ation of special relativity. In this case, the state is defined by a 

which can be written as
is the Poisson bracket. In this representation, the generators of Lorentz transformation are given by

The kinematical variable 


Explicitly, we then note a separation of generators of symmetry, as


For


The representations of the Lorentz algebra, given in Equation (5) has been analyzed in the literature [21] . However, considering the set of constitutive elements
Then we can define

Now we can calculate the values of the constants a, b, c and d, leading to a representation of the Poincaré-Lie algebra by introducing the generator
In order to get a representation of the Lorentz-Lie algebra, given by Equation (5), the constants a, b, c and d in Equation (6) have to satisfy the following condition
4.2. Quantum Mechanics
A mechanical theory describing the movement of one quantum particle is given by the following set, S, of con- stitutive elements.
CE1. Reference systems. A reference systems is defined from points such that the mapping 
CE2. The set of kinematical variables, 








CE3. The mechanical system is a non-relativistic material point, interacting to each other by a potential. For electrons such a potential is given by the electromagnetic field.
CE4. The state of a quantum mechanical system is









CE5. Changes in the state of mechanical system. The changes in the state 
CE6. The specification of the particular mechanical system is given by a function of the state of the system, 


then used to get the causal law among states, by the variational principle, defined by action by
This leads to the Schrödinger equation describing the motion of a quantum particle. In this case the Lagrangian is

The representation of quantum mechanics in phase space has been explored starting with the Wigner for- malism, based on the notion of quasi-distribution function. In this case representations of the Galilei group in phase space has been analyzed following in parallel to the Lorentz symmetry, considered in the last Section [21] . This aspect will be developed in a separate investigation. However, it is important to note here that different formalisms of classical or quantum mechanics can be accommodated in the set of Constitutive Elements and analyzed in comparison to one another.
5. Constitutive Elements of Non-Abelian Gauge Fields
One goal in this section is to consider the Constitutive elements of non-abelian gauge-fields, in order to perform a conceptual analysis, in the next section, about the notion of mass, from Newton to Higgs. In order to fix the notation and to emphasize important aspects of our discussion, we review in the Appendix some elements of a gauge theory.
CE1. Reference systems. In a (abelian or non-abelian) gauge theory, the reference systems are taken from special relativity, i.e. the Minkowski space. The set of transformation 


CE2. The set of kinematical variables, 




The procedure of quantization is carried out, consistently, by the definition of a generating functional for correlation function of the system. With this procedure, the basic physical observables are established. In parti- cular, the cross-section of a physical process, such as the scattering of particles, can be defined and compared with experiments by using correlation functions.
CE3. The mechanical system. In quantum field theory, a mechanical system is described by a field. A gauge field will describe the process of interaction among the matter field; that is the case of the Dirac field describing electrons or quarks. The notion of mass of a field is still defined with the characteristics of a Newtonian material point with inertia, and is a Lorentz scalar, obtained from the energy-momentum tensor.
CE4. The state characterizing a field is a vector in









CE5. Changes in the state of the mechanical system. The changes in the state 


CE6. Mechanical system. The specification of a particular mechanical system is given by the Lagrangian density


where 












6. The Notion of Mass from Newton to Higgs
We analyze now the notion of mass. Our aim here is not to provided a complete historical account about the developments of the concept of mass, but describe the basic improvements in the concept of mass considering the set of Constitutive Elements (CEs). We start with the concept of mass as it was first introduced by Newton in his Principia, Book I, Definition I, as the quantity of matter [32] . In the Book I, Definition III, Newton introduce mass also as a measure of the inertia; i.e. the resistance of a particle to have its state of motion changed by the interactions with another particle (taking as an example a mechanical system described by two particles). The quantity of motion, the momentum, is introduced in Definition II. As emphasized first by Poisson, the notion of material point (or material particle) was implicitly given in the Newton’s definition of mass. Such a notion was generalized also by Newton, considering problems in hydrodynamics, following the Pascal’s achievements. From the XVIII Century on, with Euler, Lagrange, Laplace, Hamilton and Poisson, a new formalism for classi- cal mechanics is constructed, using new concepts such as energy and gravitational potential. Later, the notion of mass was included in concepts such as the energy momentum-tensor, in order to accommodate the mechanical description of the continuum media. All these concepts were then generalized in two aspects: to accommodate relativistic particles and subatomic physics.
Considering the mechanical constitutive elements, the notion of mass arises as an element defining the characteristics of a particle, taken as a primitive concept. As such, mass has to be an invariant under the space- time symmetry



Considering the particle-physics standard model, the mass is introduced by the Higgs mechanism of spontane- ous symmetry breaking. As we have observed in the previous section, the gauge field is a zero mass-field by the definition of the gauge symmetry. The original Lagrangian can be improved by introducing a Higgs field in interaction with the gauge field, in order to give rise to a mass term, exploring the concept of spontaneous symmetry breaking, in a way which is similar to the Ginzburg-Landau theory for superconductivity. Although this is an intricate and ingenious mechanism, providing to some extent an explanation for the appearance of mass, the primitive kinematical characteristic of mass is still the same. This is due to the dispersion relation of a particle, which associates the notion of mass in quantum field theory with the primitive concept of matter introduced by Newton.
7. Concluding Remarks
In this work we have characterized a mechanical theory from the point of view of six Constitutive Elements (CEs), that is: CE1, the reference systems; CE2, the kinematical variables; CE3, the mechanical system; CE 4, the state of a mechanical system; CE5, the changes in the state of a mechanical system; CE6, the specification of a (particular) mechanical system. These CEs are introduced by taking as a starting point the symmetries of space-time, which in turn is associated with measurement procedures. Such a structure gives rise to a unified description for theories of motion and has been used here to analyze the Newtonian mechanics, fluid mechanics, non-relativistic quantum mechanics, one-particle special relativity and quantum field theories.
From this structure the main results include: i) notions such as particle and fields are described under the unified perspective of a mechanical theory; ii) the demonstration that the CEs has a Lie-symmetry structure in association to the Nöther theorem for conservation laws; iii) considering the Dirac theory for relativistic Hami- ltonian mechanics, we obtain a general family of representation of the Lorentz group in phase-space; (iv) non- abelian gauge fields are taken as a representation of the six CEs and, under this perspective, the notion of mass is then analyzed since Newton―regarded as the quantity of matter and a measure of the inertia―, to Higgs― associated to the notion of spontaneous of symmetry breaking.
Some aspects of this analysis are in order. First we notice that the experimental nature of the movement leads to a specific nature of mechanics. For instance, we conclude that a crucial difference between classical and quantum mechanics is the experimental conditions imposed by the Heisenberg relations. In this case, a mechan- ical theory for subatomic systems is intrinsically different from a classical mechanics. But how far is one to the other? Indeed, from the perspective of the set of CEs, one would say that the systems are described by the same mechanical theory, where the differences are emerging from the representation. In particular, this implies that there is nothing “intrinsically quantum mechanical” with the Hilbert space. This is the case for classical theories defined in the simplectic Hilbert spaces [21] . Similar achievements are derived from the comparative analysis of a relativistic and a non-relativistic classical particle. Here the experimental condition of invariance of the veloc- ity of light imposes the Lorentz symmetry for the space-time, such that the Galilei group arises from a low ve- locity limit. From this point of view, keeping in mind the set of CEs, we conclude that the space and time sym- metries (the kinematics) used for describing a specific movement is strongly associated with our experimental capacity. In other words, depending on the prescription, we can use different kinematics, which are in turn de- fined by measurements. That means that, notions like space and time are fully specified in physics by the rela- tions among objects in movement, which is the main characteristic used for defining a measurement process. This leads us to the conclusion that the Galilei or the Lorentz symmetries are constrained by the experimental conditions; and as such, these set of symmetries are not ontological structure of the space time. This is the case of the conformal symmetry, that can be broken by the Higgs-like mechanism. Therefore, considering the set of CEs, a theory is valid by itself in a domain defined by the experimental characterization of the movement. This establishes a picture of relations among theories, that combines symmetry and representations. Discarding expe- rimental evidences, one can extrapolate such a picture in different directions, which can be mathematically con- sistent, but can no longer be called a mechanical theory.
Finally, it is important to mention that, the structure of the CEs can be extended to equilibrium thermody- namics and thermal quantum field theories, by using thermofield dynamics [21] [33] . This analysis is in progress and will be presented elsewhere.
Acknowledgements
The authors thank F. C. Khanna, for the discussions and for his interest in this work, and CNPq of Brazil, for financial support.
References
- Jammer, M. (1954) Concepts of Space. Dover, N. York.
- Jammer, M. (1974) The Philosophy of Quantum Merchanics: The Interpretations of QM in historIcal Perspective. John Wiley and Sons, N. York.
- Brida, G., et al. (2011) Foundations of Physics, 41, 305. http://dx.doi.org/10.1007/s10701-009-9396-4
- Omnès, R. (2013) Foundations of Physics, 43, 1339. http://dx.doi.org/10.1007/s10701-013-9750-4
- Fox, M. (2006) Quantum Optics, an Introduction. Oxford University Press, Oxford.
- Di Domenico, A., et al. (2012) Foundations of Physics, 42, 778. http://dx.doi.org/10.1007/s10701-011-9575-y
- Brooke, J.A. (1984) International Journal of Theoretical Physics, 23, 783. http://dx.doi.org/10.1007/BF02214066
- Halabi, T. (2013) Foundations of Physics, 43, 1252. http://dx.doi.org/10.1007/s10701-013-9743-3
- Khrennikov, A. (2010) Foundations of Physics, 40, 1051. http://dx.doi.org/10.1007/s10701-009-9392-8
- Olavo, L.S.F. (2004) Foundations of Physics, 34, 891. http://dx.doi.org/10.1007/s10701-009-9392-8
- Olavo, L.S.F. (2000) Physical Review A, 61, Article ID: 052109. http://dx.doi.org/10.1103/PhysRevA.61.052109
- Olavo, L.S.F., Lapas, L.C. and Figueiredo, A.D. (2012) Annals of Physics, 327, 1391-1407. http://dx.doi.org/10.1016/j.aop.2012.01.004
- Olavo, L.S.F. (2014) Quantum Mechanics: Principles, New Perspectives, Extensions and Interpretations. Noca Science, New York.
- Smolin, L. (2012) Foundations of Physics, 42, 1239-1261. http://dx.doi.org/10.1007/s10701-012-9666-4
- Prugovečki, E. (1984) Stochastic Quantum Mechanics and Quantum Spacetime. Reidel, Dordrecht. http://dx.doi.org/10.1007/978-94-009-4492-3
- Bacry, H. and Levy-Leblond, J.M. (1968) Journal of Mathematical Physics, 9, 1605. http://dx.doi.org/10.1063/1.1664490
- Santana, A.E., Matos-Neto, A. and Vianna, J.D.M. (1994) Hadronic Journal, 17, 539.
- Rovelli, C. (2014) Foundations of Physics, 44, 91-104. http://dx.doi.org/10.1007/s10701-013-9768-7
- Oliveira, M.D., Fernandes, M.C.B., Khanna, F.C., Santana, A.E. and Vianna, J.D.M. (2004) Annals of Physics, 312, 492-510. http://dx.doi.org/10.1016/j.aop.2004.03.009
- Brading, K. and Castellanis, E. (2003) Symmetry in Physics: Philosophical Reflections. Cambridge University Press, Cambridge.
- Khanna, F.C., Malbouisson, A.P.C., Malbouisson, J.M.C. and Santana, A.E. (2009) Thermal Quantum Field Theory: Algebraic Aspects and Applications. World Scientific, Singapore.
- Khanna, F.C., Malbouisson, A.P.C., Malbouisson, J.M.C. and Santana, A.E. (2014) Physics Reports, 539, 135-224. http://dx.doi.org/10.1016/j.physrep.2014.02.002
- Levy-Leblond, J.M. (1963) Journal of Mathematical Physics, 4, 776. http://dx.doi.org/10.1063/1.1724319
- Levy-Leblond, J.M. (1967) Communications in Mathematical Physics, 4, 157-176. http://dx.doi.org/10.1007/BF01645427
- Levy-Leblond, J.M. (1967) Communications in Mathematical Physics, 6, 286-311. http://dx.doi.org/10.1007/BF01646020
- Ludwig, G. and Thurler, G. (2006) A New Foundation of Physical Theories. Springer, Berlin.
- Weinberg, S. (2011) The Quantum Theory of Fields I. Cambridge University Press, Cambridge.
- Peskin, M.E. and Schroeder, D.V. (1995) An Introduction to Quantum Field Theory. Addison-Wesley, New York.
- Toll, J.S. (1956) Physical Review, 104, 1760-1770. http://dx.doi.org/10.1103/PhysRev.104.1760
- Schroer, B. (2012) Foundations of Physics, 42, 1481-1522. http://dx.doi.org/10.1007/s10701-012-9676-2
- Plácido, H.Q., Bunchaft, R. and Santana, A.E. (1992) Hadronic Journal, 15, 225-238.
- Newton, I. (1995) The Principia. Prometheus Book, New York.
- Umezawa, H. (1993) Advanced Field Theory: Micro, Macro and Thermal Physics. American Institute of Physics, New York.
Appendix
In this appendix we present a brief review of basic facts of non-abelian gauge theories in order to emphasize the Constitutive Elements structure. The Lagrangian of the free Dirac field describing 

where 



















where repeated Latin indices are summed. Since this transformation 
where 









The set of symmetries is specified by
where 

The Lagrangian 










where the following definitions are used. (i) The term 
(ii) Using the fact that 

The gauge invariance of 


For infinitesimal transformation, where

Then we obtain the expression

where 


In this equation, each 

There is an arbitrariness in the definition of








The final results are independent of 



















