Received 8 October 2014; revised 2 November 2014; accepted 25 November 2014

ABSTRACT

This contribution is the third of a series of articles devoted to the physics of discrete spaces. After the building of space-time [1] and the foundation of quantum theory [2] one studies here how the three fundamental interactions could emerge from the model of discrete space-time that we have put forward in previous contributions. The gauge interactions are recovered. We also propose an original interpretation of gravitational interactions.

Keywords:

Gauge Interactions, Gravitation, Mond Theory, Cosmological Constant, Principle of Equivalence

1. Introduction

the particle to particle interactions are carried by three sorts of fields, the electroweak field, the strong field, and the gravitation field. The most striking feature is the enormous difference between their intensities. The electric force is stronger than the gravitation force by more than forty orders of magnitude. This is the hierarchy problem.

We have put forward in [1] a model of discrete space-time where the universe is comprised of the simplest physical systems that one can imagine, namely the cosmic bits. The cosmic bits interact through 2-bodies (binary) random links such as 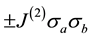and 4-bodies (quarternary) random links such as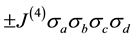. We associate the gauge interactions (electroweak and strong) with 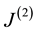and the gravitation interactions with. This will be the guideline of this contribution.

The article is, accordingly, divided in two main sections. In the first section we show how the gauge symmetry interactions naturally emerge from the model of discrete spaces that we propose. In the second section we introduce a new interpretation of gravitation based on a mechanism, somehow similar to the Van der Waals interaction, where quantum wave fluctuations play the role of electric dipole fluctuations.

2. Gauge Interactions

2.1. The Yang-Mills Theory of Interactions: A Reminder

According to Yang-Mills theory [3] , the physical space is not limited to the usual 4-dimensional continuum: to every point of the continuum one must also associate an internal space. Then the physical space becomes a fibre bundle, a space that can be locally defined as the Cartesian product of two manifolds, the fibres and a basis. In the Yang-Mills fibre bundle the usual 4-dimensional continuum plays the role of fibres, and the internal spaces the role of a basis of the fibre bundle.

Whereas a position increment dx is enough to define the derivative operator in a 4-dimensional continuous space that is into a fibre, in a fibre bundle one must also take into account an increment 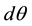between the internal spaces of neighbouring world points. Then the usual derivative 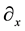is to be replaced by a covariant derivative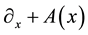. The term 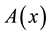is called a parallel displacement. Some symmetry transformations may be defined in internal spaces and, if physics is left invariant under these transformations, there are called gauge transformations. Yang-Mills theory assumes that the gauge transformations are Lie groups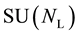, where 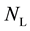is the dimension of the matrix representation of the group. The theory associates a particular interaction to a given Lie group: U(1) for electromagnetic interaction, SU(2) for weak interactions, and finally, SU(3) for strong interactions. Each Lie group then introduces a specific parallel displacement 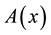called a gauge field.

In this section we show that the Yang-Mills theory can be transposed in the framework of the model of discrete spaces that we propose. The ill-defined concepts used by the Yang-Mills theory, such as the notion of internal spaces, are now given a physical meaning. Moreover unanswered questions posed by this theory, for example the choice of the relevant Lie groups, are also given a response.

2.2. Gauge Symmetry

In the model of discrete spaces that we put forward, the universe is made of basic cells called world points, and the physical points of the Yang-Mills theory are similar to world points. The internal space of a world point is the space spanned by its possible states. This space is d-dimensional with 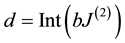(for more information see [1] ). A gauge symmetry group is a group whose elements leave physics unchanged. Nothing determines a particular orientation of the d axes of coordinates in the internal space of world points. Therefore any permutation of axes or any unitary transformation of the internal space must leave physics unchanged. Physics, therefore, must be invariant with respect to permutations of axes, that is, to the operations of symmetric permutation group S₄ (since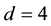). It must also be indifferent to unitary transformations U(4) of the internal space. S₄ and U(4) are gauge symmetry groups of the model of discrete spaces. The relevant symmetry groups, however, must comply with both gauge groups. The group S₄ has five irreducible representations, namely two 1-dimensional representations (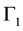and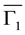), one 2-dimensional representation, and two 3-dimensional representations (and) (the table of characters of is given in [1] ). The particles that transform according to are fermions and those that transform according to and are bosons [2] . The operations of U(4), however, must be compatible with the representations of and therefore there are three, and only three, relevant unitary gauge symmetry groups:

a) U(1) which is associated with irreducible representations or.

b) SU(2) which is associated with irreducible representation.

c) and, finally, SU(3) which is associated with irreducible representations or.

There are no other gauge groups.

2.3. Covariant Derivatives in Discrete Spaces

All properties of discrete spaces are derived from a very general Lagrangian, where is the state of the physical system, that is a set of states with of the N world points i of the physical system. A state is a 4-dimensional vector:

.

The Lagrangian writes

(1)

is square, random, matrix that describes the world points to world points interactions. is a set of N matrices that describes the interactions between the four components of (for a more detailed presentation of the model see [1] and [2] ).

The notion of partial derivatives is introduced in discrete spaces through the matrix D obtained by factorizing the operator of Lagrangian (1).

According to the LDU (Lower triangular, Diagonal, Upper triangular) Banaciewicz theorem may, indeed, be written as where D is a random, , upper triangular matrix that can be interpreted as a discrete differential operator. An increment along the axis of component of state of world point i is defined by

,

and the partial derivative by

(2)

an operation that can be symbolized by in the usual 4-dimensional continuum. is the size of a world point.

Physics must be left unchanged under the operations of a unitary gauge group. As discussed above, the physical system is a fibre bundle where the fibres are given by D and the basis by. In a specific transformation in Equation (2) becomes where, an element of Lie group, is given by

is a unitary matrix and therefore where C stands for hermitian conjugation. The operators t_a are the generators of and the parameters determine a particular transformation of

the internal space of world point i. We consider infinitesimal transformations. A

first order expansion approximation of is:

.

Then the derivation operation becomes

. (3)

Finally, one finds a covariant derivative indeed., one of the associated

parameters, materializes a gauge field.

2.4. The Lagrangians of Gauge Fields

In the Lagrangian (1), rewritten as

(4)

one replaces the operators D by their covariant expressions (3). Then (4) is made of three terms.

a) We first recover the Lagrangian term of the free quantum particle field:

.

b) Then we obtain the Lagrangian term of gauge fields

.

If we only consider local contributions we must look at terms with. Since this expressions becomes:

.

c) and finally, a local interaction term between the particle and the gauge fields:

.

2.5. Electro-Weak Interactions

In this section we recover the results of the GSW (Glashow, Salam, and Weinberg) theory of electroweak interactions [4] . The interest of this section is less in the derivation of the theory, which is classical, but, rather, in the answers to questions posed by this theory.

According to the GSW theory the gauge group for leptons would not be U(1) or SU(2) or SU(3) but a combined group, namely. We consider the contribution of this gauge symmetry group to the local Lagrangian where the vacuum state is the state that minimizes the local Lagrangian

,

with

under the constraint (see [1] ). One finds

. (5)

The contribution writes

.

Here the matrices are the generators of Lie group. The generators of SU(2) are the three Pauli matrices and the generators of U(1) are scalar numbers. For electroweak interactions one has, accordingly,

.

From a mathematical point of view this expression is meaningless because it mixes a scalar with two dimensional matrices. The problem is resolved by introducing the simple following transformation between the scalar 1 and the two dimensional matrix.

.

The value of the electroweak Lagrangian in vacuum is then given by (with c = 1)

. (6)

Instead of a 4-dimensional real representation of, a two dimensional complex representation may also be used, namely

.

In this representation the vacuum state is written

.

By introducing this state in Equation (7) and by defining

and

one has

.

Finally with

the results of the Glashow, Salam and Weinberg (GWS) theory are recovered. The eigenvalues of the last 2-dimensional matrix are associated with the field and associated with the electromagnetic field A. The electroweak interaction therefore compels the photon mass to be strictly zero but this result only holds for the chosen vacuum (5). The GSW theory, however, does not answer the following questions.

a) What is the mechanism that binds the groups U(1) and SU(2)?

We shall not treat that subject here in detail but it can be shown that the entire organization of particles of the Standard Model can be recovered by assuming that the seed of a particle does not involve a single world point but a pair of world points, instead, one with a bosonic character, the other with a fermionic character, an idea close to super-symmetric (Suzy) approaches. According to this interpretation the leptons would transform as and the quarks as where are three irreducible representations of the symmetric group of permutations of four objects. Combined with the unitary symmetry group U(4) the gauge group of leptons is accordingly. The Suzy mechanism has been introduced to (partly) remedy the divergences that appear in Feynman diagrams but the price to pay is a doubling of the number of particles (bosinos that are fermions associated with bosons and sfermions that are bosons associated with fermions). Here there is no need for such a doubling because, in our approach, the ordinary particles are made of pairs of bosonic and fermionic world points and are super-symmetric in essence. For the time being no super-symmetric particles has been experimentally found. One also could say that the success of the GSW theory is a good support of our Suzy-like model of particles.

b) What is the vacuum state?

The vacuum state is chosen in the GSW theory so as to make the photon mass vanish. How to justify this choice whereas the Higgs vacuum states

with are all equivalent?

In our interpretation the vacuum state of an isolated world point is necessarily asymmetric. It is given by Equation (6) which is precisely the vacuum state used in the GSW theory.

c) How to determine the Weinberg parameter?

The vacuum state is fully oriented along the time axis. The three Pauli matrices are associated with the three space dimensions. The three dimensions of space and the time dimension constitute an affine space with a dilatation factor given by c. It is then convenient to assume that. In [1] we have seen that the (dimensionless) speed of light is given by (with) and that the dimensionality d of space- time is determined by. The Weinberg angle is defined by

The experimentally accessible parameter is

.

Since, one has and therefore

The experimental value is

which is consistent with the prediction. With this value as a datum we find

3. Gravitation

3.1. A Link between Discrete Spaces and General Relativity

A state of vacuum with, given by Equation (6), for all world points i is not acceptable because such a vacuum would have no space dimensions. One observes that is not allowed because it ignores the uncertainty principle or, more precisely, the notion of zero point motion. Let be the state of the fundamental mode of the harmonic oscillator that represents the dynamics of the electromagnetic field. is a

Gaussian function. Then vacuum is defined as a state with

with. Vacuum then recovers spatial dimensions.

The central hypothesis of general relativity is that the metric matrices are site dependent in space-time and that these modifications are caused by masses and, more generally, by non vanishing energy densities. In our model this hypothesis transforms the vacuum metric matrix into. The developed Lagrangian of a free particle in a space is then given by

.

The length increments of space along the dimension at world point i are given by

where l^* is the size of a world point. This gives

.

In the continuous limit the expression reads

.

This action is the starting point of General Relativity. The main conclusions of General Relativity, in particular the Einstein equation, may then be derived by using the usual (covariance) arguments. More precisely General Relativity may also be seen as a gauge field theory where space-time is analogous to a fiber bundle. The fibers of the bundle are (approximate) copies of the Minkowskian metrics and the basis of the bundle is space- time itself. This is exactly the scheme that appears in the present approach. The fibers are (approximate) copies of and the basis of the bundle, that is the connection between the fibers, is provided by the matrix. In the present approach there is no longer a contradiction between quantum and general relativity theories because both theories become irrelevant below the metric limit l^*, quantum theory because a quantum state can no longer be defined and general relativity because the metric matrices disappear.

3.2. Weak Gravitation Fields

Let us now consider weak gravitation fields. In weak gravitation fields the local metric matrix may be written as

where is the four dimensional coordinate associated with world point i and. The Lagrangian of a free particle is modified accordingly

.

The second term on the right hand side may be seen as a three-body interaction where the field is scattered by a tensor field. If the perturbation is assumed to be so weak that the modifications of the (inertial) masses of particles are negligible, the Lagrangian is not modified either, and one must write

,

that can be satisfied only if

.

This expression is a propagation equation that describes the dynamics of a massless tensor field implying 10 independent components. Let us consider the trace of this tensor (its dilatation component)

.

Its dynamics is then given by

.

This is the propagation equation of a massless gravitation wave travelling at the speed of light c. Its propagator writes

. (7)

3.3. Quantum Mechanics in Curved Spaces

In this section we look for the quantum dynamics of a particle evolving in such curved spaces. The Lagrangian

is minimized under the set of N constraints. The expression to be minimized is

where is a site dependent Lagrange multiplier. This yields the following eigenvalue equation

.

Making explicit every component of world point polarizations, this equation gives

.

Following the argument already given in [1] the 4-dimensional wave function satisfies the following equation

.

This equation describes the quantum dynamics of a particle in the framework of the theory of general relativity. In flat spaces, the Klein-Gordon equation is recovered. This description of quantum states in gravitation fields is similar to the approach called “quantum mechanics in curved spaces” [5] . There is, however, an essential difference: the mass of the particle is site-dependent, , which makes the calculations much more difficult. In strongly distorted space-time metrics, the particle can even lose its identity.

3.4. Indirect (Fluctuation) Interactions

Particles interact through gauge interactions by an exchange of bosonic particles (photons, vector bosons or gluons) that result from the quantization of gauge fields. These are direct interactions, but besides those interactions there are also indirect interactions where two physical systems interact through fluctuations of their internal structures.

The best known example of indirect interactions is the Van der Waals interaction. In physical systems housing positive and negative electric charges, the centres of gravity of positive and negative charges may not match, giving rise to fluctuating electric dipoles. The dipoles interact and some dipole orientations lower the energy, the closer the systems the larger the energy lowering. The result is an attractive force that decreases as.

Another example is the nuclear indirect interaction between nucleons. The mechanism at work arises from the fluctuations of quark colour charges. The fluctuations are transmitted between the various quarks that compound a nucleus through gluons (which are colour charged). The result is a strong, attractive, short range interaction.

Since the fluctuation interactions are always attractive and since the gravitation interaction is also attractive, we suggest that the gravitational interaction is an indirect interaction. The polarization of a world point, in fact the quantum wave, may indeed fluctuate due both to cosmic noise b and finite size n of a world point.

3.5. Newton Gravitational Attraction

The polarization amplitude of a world point is given by the thermal average of an order parameter s

with. The cosmic noise parameter b may be interpreted as the inverse of a temperature. We have seen in [1] that the partition function of this system writes

where

.

The polarization is therefore a random Gaussian variable with a mean square deviation given by

. (8)

The fluctuations vanish when n, or b, or J, goes to infinity. The vanishing of fluctuations characterizes the so- called mean field approximation. Then the realized state is the state that minimizes the free energy, a technique called saddle point approximation. A large fluctuation of destabilizes the eigenstates solutions of the equation. If is a random Gaussian variable with standard deviation, (where is a constant) is also a random Gaussian variable with standard deviation and therefore the relevant standard deviation of the world points polarizations must be modified along the following formula

.

The eigenvalue of a system where a world point i houses a particle P is. Since (see [1] ) the fluctuations modify the polarization of world point i of the system by an amount

where is a factor of the order of 1.

Similarly, the polarization perturbation of a world point j housing another particle Q is

.

The propagation of gravitation waves creates an interaction between the two particles P and Q that, owing to the weakness of vertices, may be calculated by using a low order perturbation expansion. The lowest order writes

.

By using Equation (8) the static gravitation interaction is given by

. (9)

The Fourier transform of in a d-dimensional space behaves as. This expression yields for d = 3.

.

Finally, the Newton expression of attractive gravitational forces is recovered:

. (10)

The gravitation constant is proportional to 1/n. Let us see how the experimental value of the gravitation constant gives an indication as regards the orders of magnitude of n and l^* the size of a world point.

The Planck length is given by. is the Planck mass:. One has and. is the smallest length that has still a physical meaning. Since a cosmic bit is the most simple system one can imagine, one assumes that is the (non phy- sically measurable) size of a cosmic bit.

In other respects, the electric potential between two electrons at a distance is

whereas the gravitational potential between these two electrons is.

With and the ratio between the two potentials is

(is the fine structure constant). According to the present interpretation this ratio varies as. Assuming that the number of bits belonging to a world point is then of the order of

,

a very large number indeed. n is determined by the ratio of second order comic bits interactions to

fourth order interactions and, more precisely, by minimizing a Landau-type free energy

[1] .

One has and as assumed above.

This large difference between and would explain the large intensity gap between the gauge interactions and gravitation interaction (the hierarchy problem).

The number of cosmic bits in a world point is given by

that is and therefore

,

the size scale of world points that has been used so far. The energy corresponding to this size is

very far (by four orders of magnitude) from the possibilities of available machines even those of the LHC.

Finally the size of a coherent domain [2] , that is the limit of classical mechanics, is such that

and

about two hundred times the size of an hydrogen atom.

3.6. Mond Theory

The anomalous motion of outer stars in a galaxy has led the astrophysicists to introduce an invisible matter that they called dark or hidden matter [6] . No such matter has been directly found so far and its only experimentally measurable effect is the bending of light rays, a consequence of general relativity. Milgrom has put forward another explanation for the anomaly. At very large distances the Newton dynamics would have to be modified [7] (Mond is for Modified Newton dynamics). Instead of the classical Newton attraction

Milgrom suggests that one must write

with for, and for. At large distances, the gravitation force is then given by

is the Milgrom range. There is, in principle, a way to deduce the parameter from experimental observation. In Newton dynamics, the speed of stars in a galaxy disk is given by, that is

.

In Milgrom dynamics, that is

,

a constant as observed. can be measured and one has. The problem is that one does not know the value of M the mass of the galaxy bulb.

Since the motion of stars in the disks of galaxies is determined by the Mond dynamics the Milgrom parameter must be of the order of, or less than, the galactic bulbs radii. The galaxy bulbs diameters are of the order of (light year) to. We chose the value but the value of could be smaller.

The model of discrete universe that we propose can provide an explanation of Mond theory based upon the possible modifications of world point dimensionality d under the influence of polarization fluctuations. Let us recall that the internal space of a world point may be considered as a d-dimensional space where the polarization is a d-dimensional vector [1] :

and. The Lagrangian of a world point is expressed in term of polarization components and the partition function Z in term of their thermal averages. Z, given by

,

has been computed in [1] . The result is

.

Every component fluctuates with a standard deviation

. (11)

If the fluctuations of one component of exceed the associated dimension is lost, and the internal space of world point, instead of being a (3 + 1)-dimensional, becomes a (2 + 1)-dimensional space. The proportion of such world points is given by

where is the Gauss distribution

.

Then by letting one has

.

Since we find

.

The form of the gravitation interaction associated with (2 + 1)-dimensional world points is modified because the Fourier transform (7) is now 2-dimensional. The potential in a 2-dimensional space becomes

.

Finally, the Milgrom attractive gravitational forces is

.

As a whole the gravitation interaction becomes

with. Then if and if as assumed by Mil-

grom.

The disappearance of a dimension may be interpreted as the shrinking of the lengths associated to that dimension by a factor. This reminds the shrinking of non observable dimensions in string theories (where 10 or 11 dimensional spaces are reduced to the classical 4-dimensional spaces) with the difference that we have here a mechanism that really put the process at work. For example a standard length is now seen as a length.

3.7. Cosmological Constant

A world point i eventually loses another dimension if the fluctuations perturb simultaneously two field components and of the polarization of i. The probability for such a situation to occur is . Then the internal space of world point becomes (1 + 1)-dimensional and the interaction potential becomes

.

The associated gravitation force is

a repulsive constant force that acts as a negative pressure exactly as does the cosmological constant.

The formula gathering the various contributions to the gravitation forces is

. (12)

In Equation (13) is the cosmological constant.

Since the distance travelled by light in one year is, and, with,. Finally, which is close to the experimental observed value. The agreement is striking but it must not be taken too strictly because it depends on a poorly known parameter, the Milgrom range. The main interest of the derivation is that it seems to give the right orders of magnitude to the cosmological constant.

The distance r_M where the cosmological expansion takes the lead over the Milgrom dynamics is , a value of the order of the size of the observable universe.

3.8. On Dark Matter

Up to now the possible effect of dark matter has not been taken into account. Dark matter has been introduced to account for the rotation curves of stars gravitating at the peripheries of galaxies. The Mond theory proposes another explanation and dark matter seems to be no longer necessary. The study of galaxies clusters shows that this is not the case. The gravitation forces are, in the Mond theory, exactly known. They are central and enable an exact calculation of the motions of galaxies in a cluster of galaxies to be carried out. The observation of the galaxy cluster 1E0657-56 (the Bullet) does not support the calculations. Dark matter is still necessary. Moreover dark matter is also necessary to account for the formation of galaxies. There is, however, no direct experimental evidence for their material existence except for their gravitational lens effects.

The model of discrete space-time that we put forward may provide another interpretation. Let us consider the metric matrix of the model [1] . It writes

This metric matrix is sensitive to variations of cosmic noise b and since the speed of light is given by a variation of cosmic noise b leads to a variation of the speed of light c. Space then behaves as a refractory medium and a non uniform repartition of cosmic noise is reflected by the bending of light rays exactly as gravitational lenses would do. Astrophysicists generally tend to interpret the deviations by the presence of matter although no matter is necessarily involved in the process. Given the agreement between the experimental and the computed values of the cosmological constant, a theory that does not take dark matter into account, is satisfactory, and one must conclude that the universe is flat and its dimension is everywhere. This remark does not jeopardize the existence of dark matter. We can define our universe as a set of world points where and define dark matter as regions where is in between these two limits.

3.9. Principle of Equivalence

The parameter that appears in the Klein Gordon equation is called the mass of particle P. It is given by where is the eigenvalue of the following equation

.

In the classical limit this mass is the mass parameter that appears in the Schrödinger equation and, finally, through the Erhenfest equations, the mass of the Newton equation

.

Therefore is the inertial mass of P.

is also the parameter that appears in the Newton gravitational force (9). Therefore is the gravitational mass of P. We conclude that, a proof of the principle of equivalence.

4. Discussions and Conclusions

In contribution [1] we put forward a model of discrete space-time that we consider to be a convenient framework for the description of natural phenomena. To be accepted, this statement must be supported by a proof that the model can account for the main issues of theoretical physics. Some have been studied in [1] and [2] . Here we show that the four fundamental interactions may be understood in the framework of this model. It allows a natural introduction of gauge interactions. Moreover, it suggests the idea that gravitation could be an effect of fluctuations of world point polarizations (quantum states). The fluctuations are caused, on one hand, by the finite size n of world points and, on the other, by the cosmic noise b. The former effect gives a solution to the hierarchy problem because n is so large that the gravitation forces are extremely weak compared to gauge interactions. The later, the cosmic noise b, leads to the idea that the dimensionality d is not given once and for all. Large enough cosmic noise fluctuations may result as a decrease of d. For the attractive gravitation law is that of Newton, for one finds the attractive gravitation law of Milgrom and, finally, for d = 1 + 1, one finds an extremely weak, repulsive interaction that reminds the effects of the cosmological constant. Instead of increasing d, as in string theories, we think that the physical phenomena can be better understood by decreasing d.

Obviously, the introduction of a cosmic noise must have large consequences in cosmology. Although this issue is out of the scope of this article we would like to mention briefly a few effects of b.

Below everything disappears, space, fields and particles, a situation that reminds a pre Big-Bang state.

If the speed of light becomes imaginary and so is the case of time. The concept of imaginary times has been proposed by Hawking to cope with the difficulties set by the initial state of the universe [8] . One also sees that the metric matrix becomes Euclidean which yields another solution to these difficulties [9] .

Finally the speed of light diverges for which could give a physical solution to the inflation problem.

Acknowledgements

I would like to heartily thank Pr. Bart Van Tiggelen. He does not believe in my ideas but he strongly incited me to continue.

References