Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40916,4 pages DOI:10.4236/jmp.2013.412198
Higgs Bosons, Quark Masses and Two Components of Cabibbo Angle
New York City Transit Authority, New York, USA
Email: lsitnikov@cs.com
Copyright © 2013 L. S. Sitnikov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 21, 2013; revised September 25, 2013; accepted October 24, 2013
Keywords: Hierarchy of Fermions’ Masses; The Masses and Mixing Parameters of Quarks; Cabibbo Angle; Higgs Bosons
ABSTRACT
This paper discusses the discovery and study of the functional connection between the quark masses and their mixing parameters. That allowed calculating Cabibbo angle from the known values of the masses of two lower quarks. It has been established that mixing occurs not only among lower quarks, as it was known up to now, but the upper quarks, independently, do the same. A separate mixing angle is calculated for the latter. The existence of “two Cabibbo angles”, i.e. independent mixings of upper and lower quarks, is a strong argument in favor of models with not one, but with several Higgs bosons. Only taking into account such a link, it is possible to give the unified description of the dependence of the mass on the generation number for all charged fermions (except t-quark). It turns out that increments of values 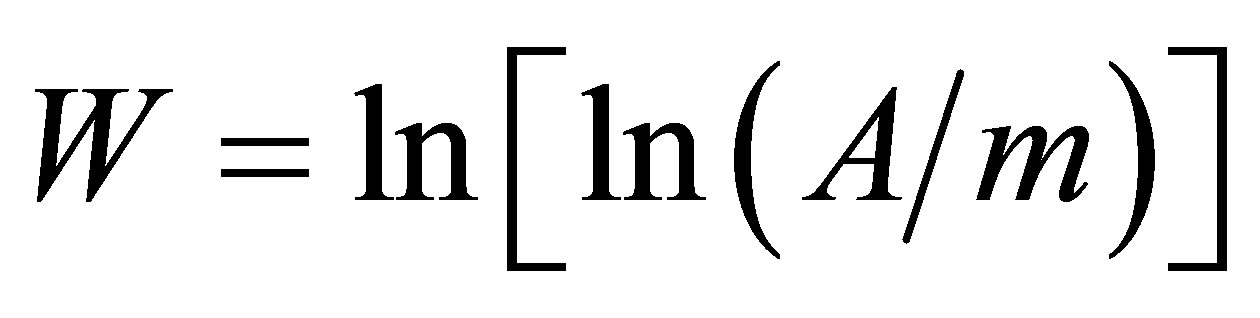 and N are linearly linked. (Here m and N—mass and generation number of fermion, A—common internal parameter of concerned fermions).
and N are linearly linked. (Here m and N—mass and generation number of fermion, A—common internal parameter of concerned fermions).
1. Introduction
In the Standard Model, there are many so-called external, free, or adjustment, parameters, the numerical values of which are known only from the experiment. These also include the quark mixing parameters, as well as mentioned in the title Cabibbo angle that describes mixing quarks of two generations. “Cabibbo angle is introduced to the theory phenomenologically only. From a theoretical point of view, the calculation of this angle is a task that is very close to the problem of determining the relations of the quark masses. At this time, however, there are no reasonable approaches to solving it” [1].
This paper examines both of these challenges and establishes a connection between the quark masses and the quark mixing parameters. In an alternative approach, they consider that the observed hierarchy of the masses of quarks is based on spontaneously broken global symmetry, linking generations of fermions [2]. However, this theory predicts the existence of Goldstein boson (so-called familon) with tightly restricted settings [2] not found experimentally. Another alternative approach is given in the dimensional model of the world [2,3]. In this model, there is only one generation of six-dimensional particles, which gives three generations of particles with different masses in four-dimensional (three-dimensional space and time) of the world).
So, in papers [4], without reference to any new entities, exotic hypotheses and models, we proposed an expression like
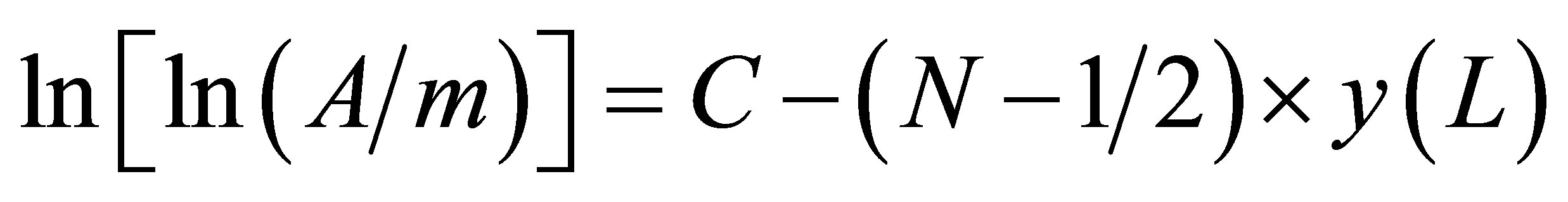 , (1)
, (1)
describing mass of a charged lepton m as a function of the number of its generation N. The values of the parameters A = 42.87 GeV, y(L) = 0.6354 and C = 2.7458 were calculated in [4] from the known masses of the charged leptons.
2. Extrapolation for Current Quarks
Let us try to generalize the solution (1) for masses of current quarks. For convenience we introduce the notation n = (N − 1/2) and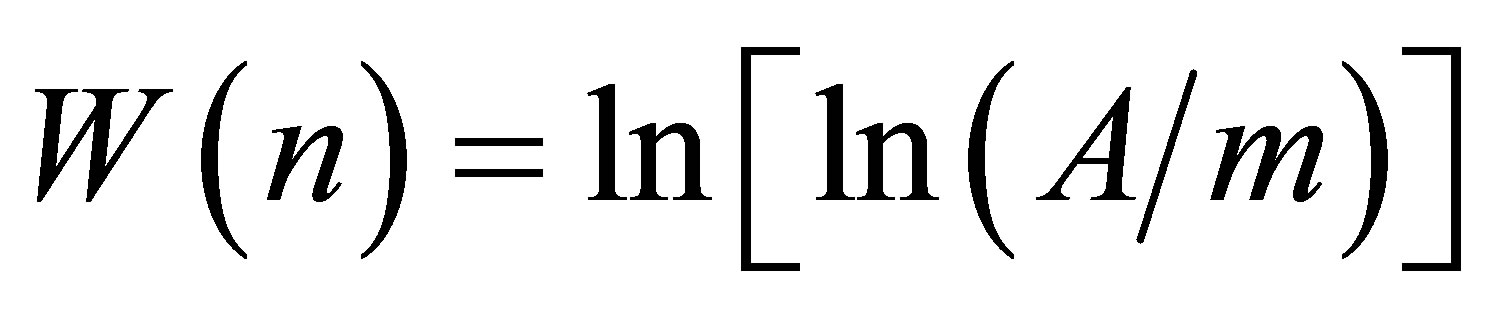 . Let us calculate the values W(n) for the quarks and charged leptons and place on the diagram (Figure 1) the data points W(n) that are marked with the symbols of corresponding particles (the solution (1) and W(n) do not exist for t-quark,
. Let us calculate the values W(n) for the quarks and charged leptons and place on the diagram (Figure 1) the data points W(n) that are marked with the symbols of corresponding particles (the solution (1) and W(n) do not exist for t-quark,
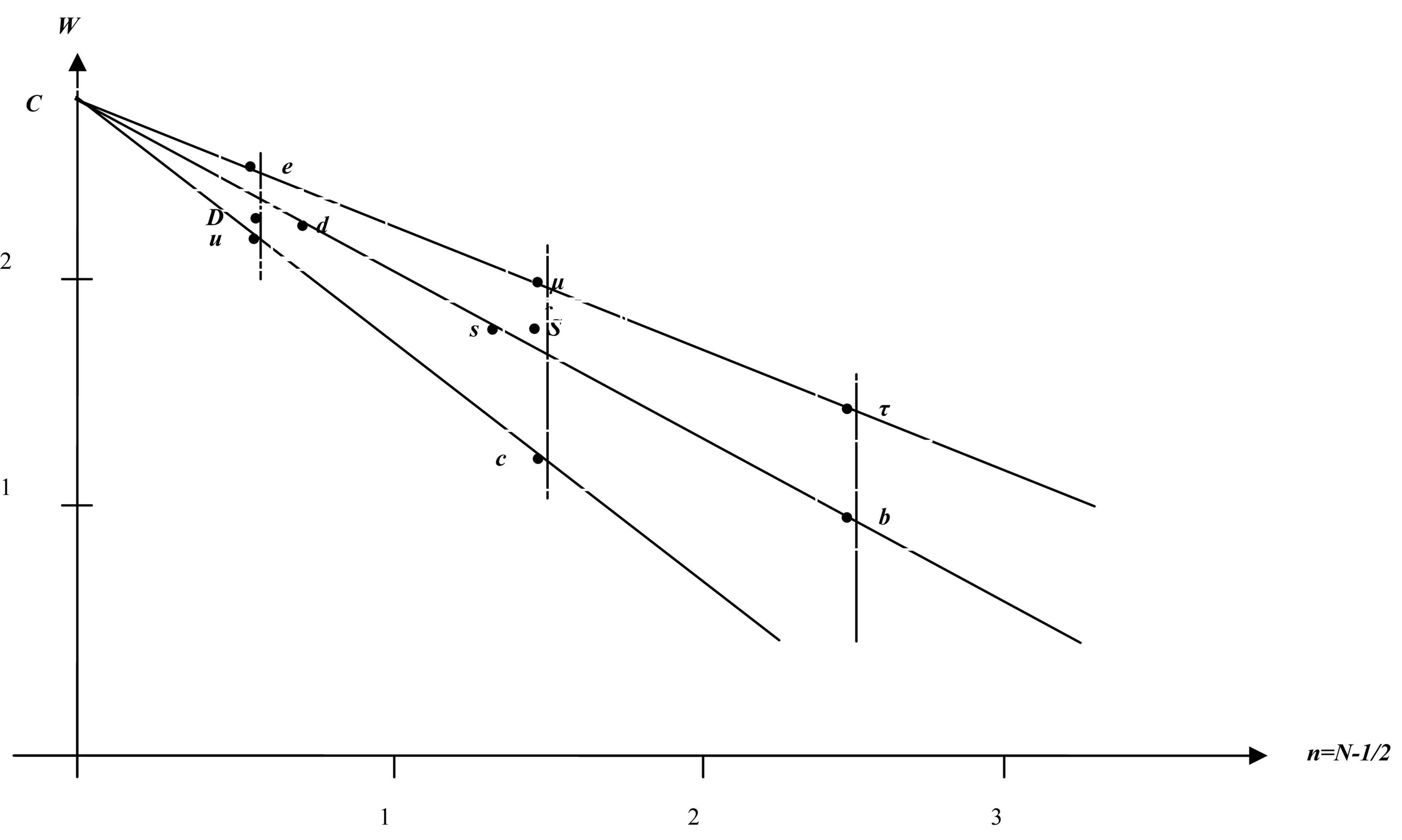
Figure 1. The increments of values 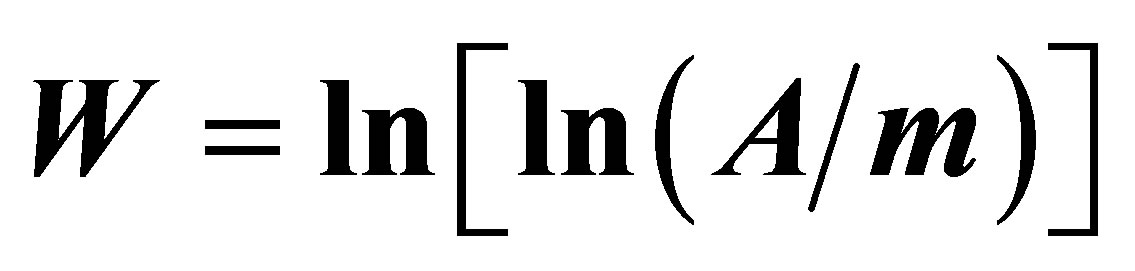 and the generation number N are linearly linked.
and the generation number N are linearly linked.
since mt > A). As can be seen from the Figure 1, the points C and W(n) of the charged leptons are placed on the one straight line, as it should be in accordance with Equation (1). The same is true for C and W(n) of the upper quarks. The points W(n) of the bottom quarks do not get in the right straight line (as a rough approximation it is straight line C-b, where the point b is determined for the tabular value of quark b mass, without taking into account its mixing with the rest of the bottom quarks). In the framework of standard model it is natural to assume that the anomalous position of the points W(n) for the bottom quarks (with respect to the points of the charged leptons and upper quarks) is related to their mixing.
Difference is made between so-called weak quark states D and S, interacting with the intermediate vector bosons, and massive quark states d and s, interacting with the Higgs bosons. From the position of the weak currents-“true particles” are the D and S states. From the position of the masses-true particles are d and s states. The difference between the former and the latter is due to the fact that “the direction in the space of bottom quarks, which is created by their interaction with the charged intermediate vector bosons, does not tally with the direction that came about through the interaction with Higgs bosons” [1]. For this reason, there arises mixing of quarks. For our purpose it is convenient to consider the weak quarks D, S, B as initial fields. In this case massive quarks d, s, b are considered to be linear combinations of the initial fields for which the mass matrix is diagonal. In the most general way, nine coefficients, characterizing the mixing, can be expressed in three Euler angles and a phase factor. When B = b, i.e. if we neglect transitions bu and bc, there remains only Cabibbo angle describing the mixing of quarks D and S:
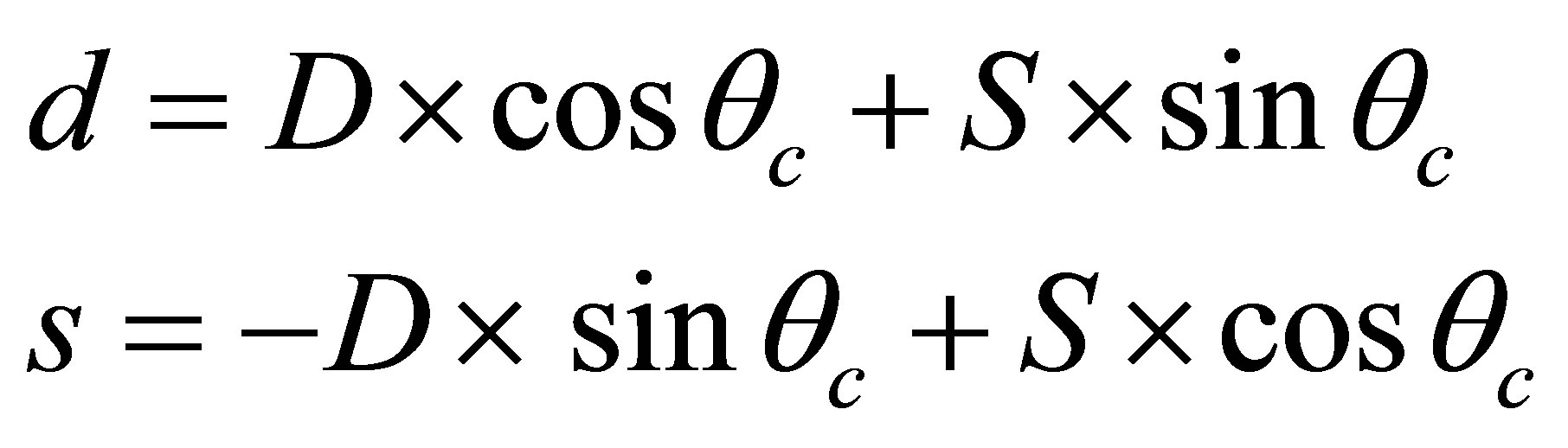 (2)
(2)
What happens to points W(n) when the quarks are “mixed”? The ordinates of the points, shown in the Figure 1, definitely correspond to the masses of particles and, therefore, cannot be modified in any way. This means that the only reason for the failure of points d and s of the quarks to fall on the right straight line may be the wrong choice of their abscissas, i.e. parameters (internal quantum numbers) n = (N − 1/2), characterizing the degree of belonging of each quark to a particular generation of N = 1, 2, 3. Therefore, we assume that the quark mixing means mixing of their quantum numbers n and the latter are described by the same formula, i.e.
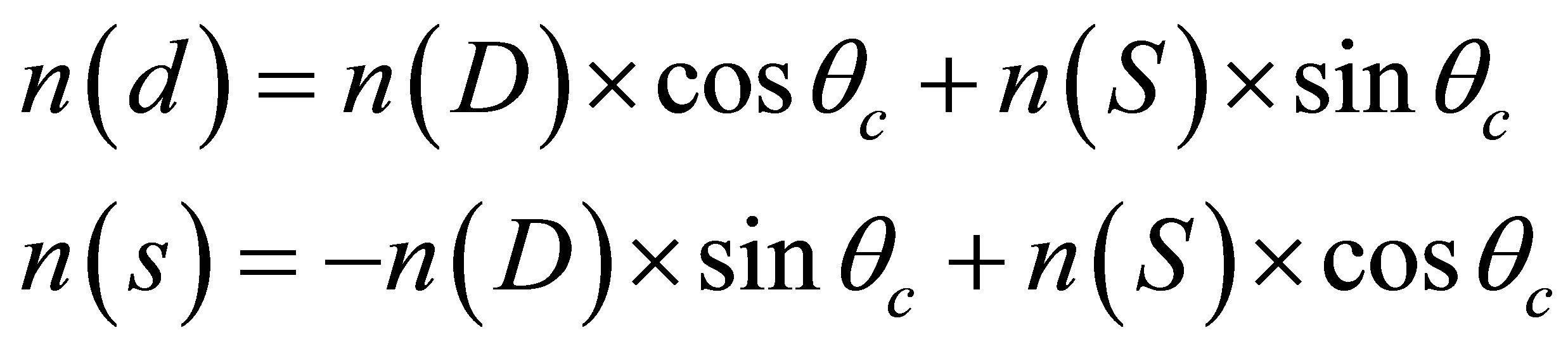 . (3)
. (3)
Using the known from experiments value of Cabibbo angle θc = 13˚, from (3) we find that n(d) = 0.825 and n(s) = 1.349. It can be seen (Figure 1) that taking into account the quark mixing (i.e. the use of fractional values of the quantum number n for d and s quarks, calculated by the Cabibbo angle) ensures for points W(d) and W(s) hitting the straight line c-b and, thus, allows to uniformly describe the masses of all charged fermions.
Now, let us reverse the sequence of the above considerations: assuming, by analogy with the charged leptons and upper quarks, the points W(n) for massive bottom quarks are clearly stationed on a straight line passing through the point C, let us try to calculate the value of the mixing angle of lower quarks.
In the two-dimensional space of bottom quark states (the plane of Figure 2) the vectors are shown of weak D and S and massive d and s states. The state vectors are related to each other by Equations (3). Angle f of each vector (Figure 2), relative to the axis n, associated with the direction of action of the Higgs bosons, is defined as
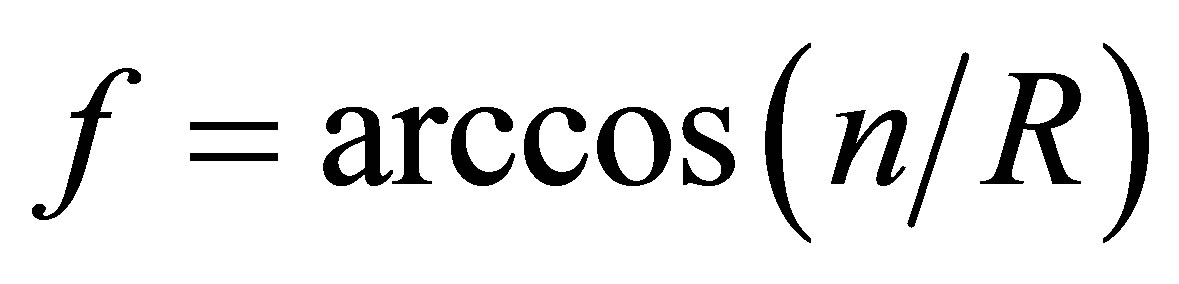 (4)
(4)
Here
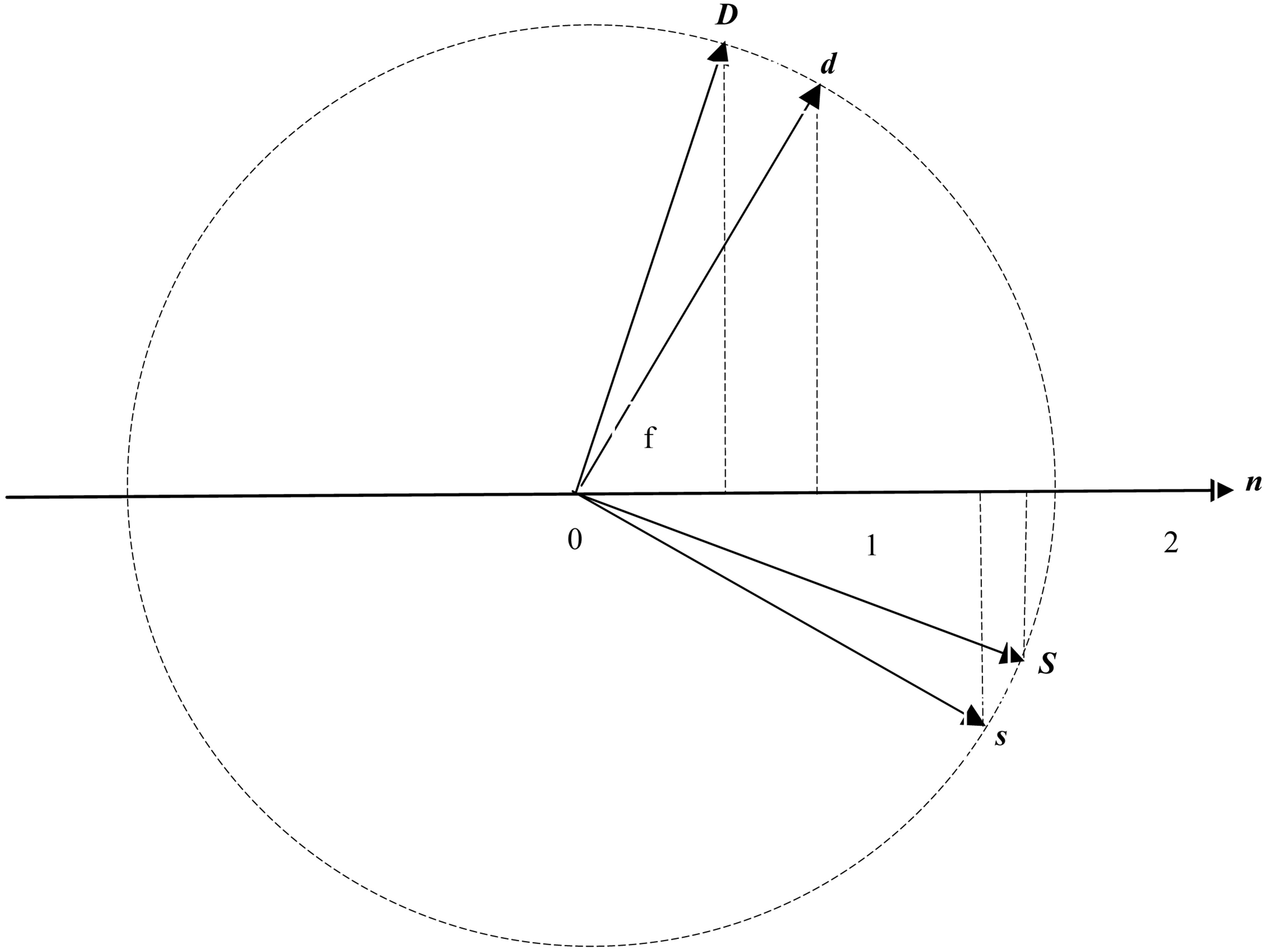
Figure 2. Vectors of weak D and S and massive d and s states.
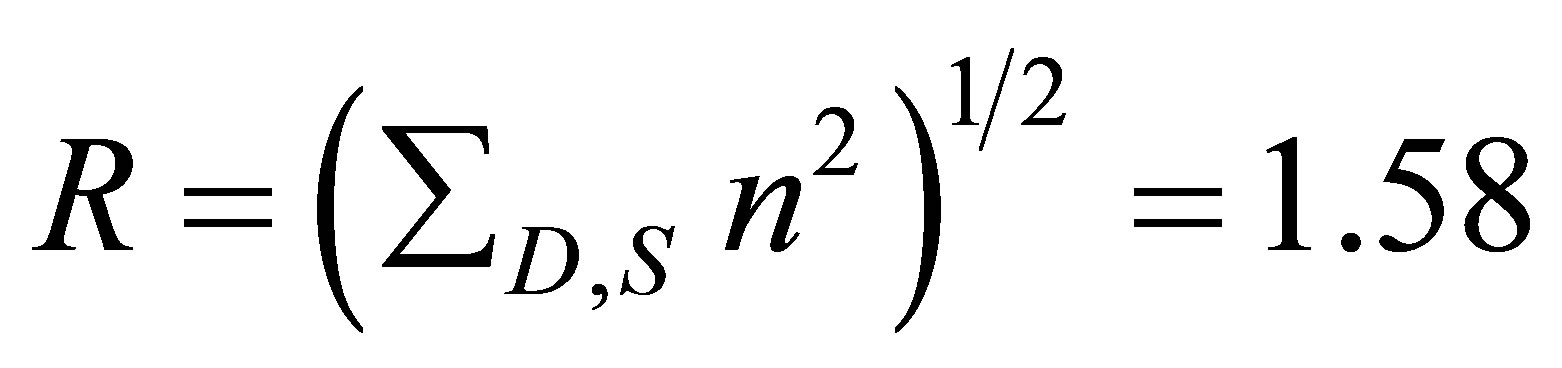 (5)
(5)
For weak states D and S values n are known (½ and 3/2, respectively), so angles f for them are readily determined. It is harder to calculate the angles of the state vectors d and s, as for the latter we do not know the values of n. But, on the other hand, for them we know the masses and, consequently, the values of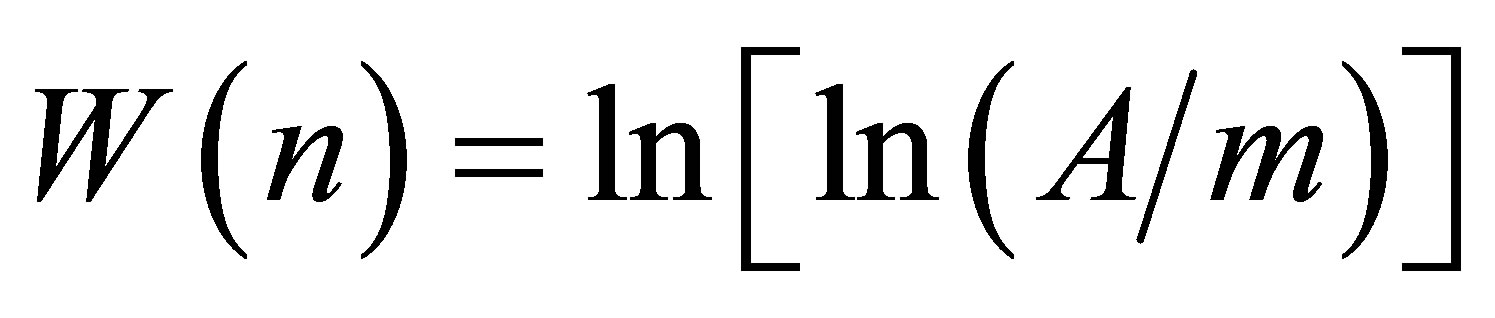 . This allows, using the expression (1), to determine n as
. This allows, using the expression (1), to determine n as
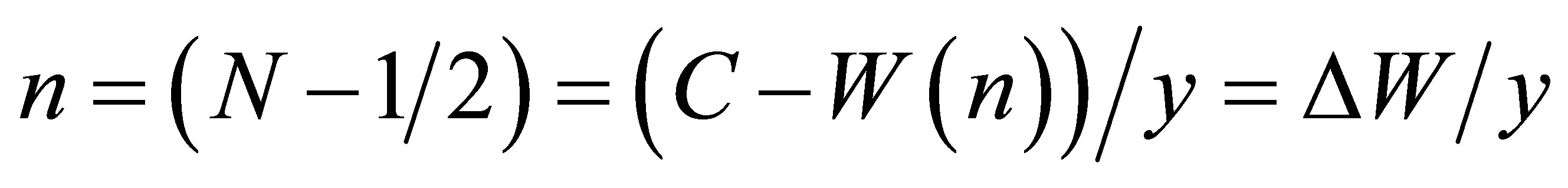 (6)
(6)
Note that the parameter y (the slope of the line in Figure 1), in contrast to the universal values of A and C (see Equation (1)), has different values for the charged leptons, bottom and top quarks.
From the known properties of the mixing matrix it follows that
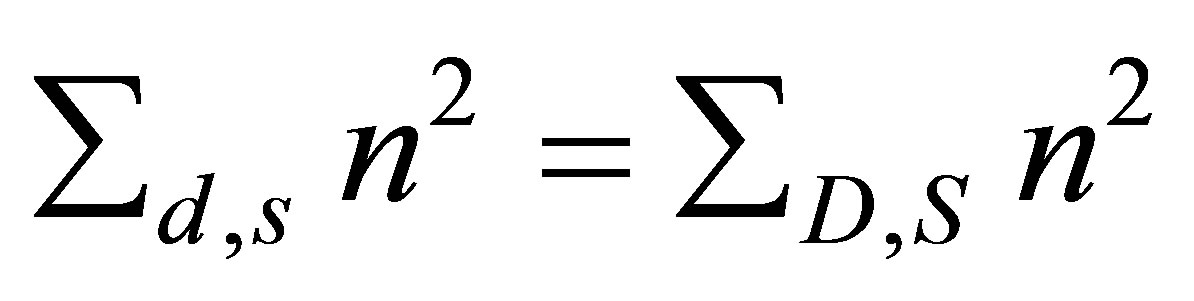 (7)
(7)
Substituting in the left side of the latter expression the equivalent from (6) for n, we obtain
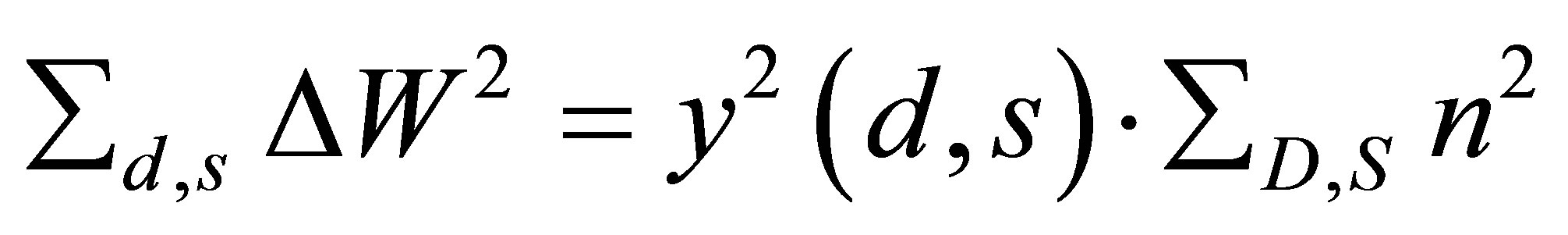 (8)
(8)
whence it follows
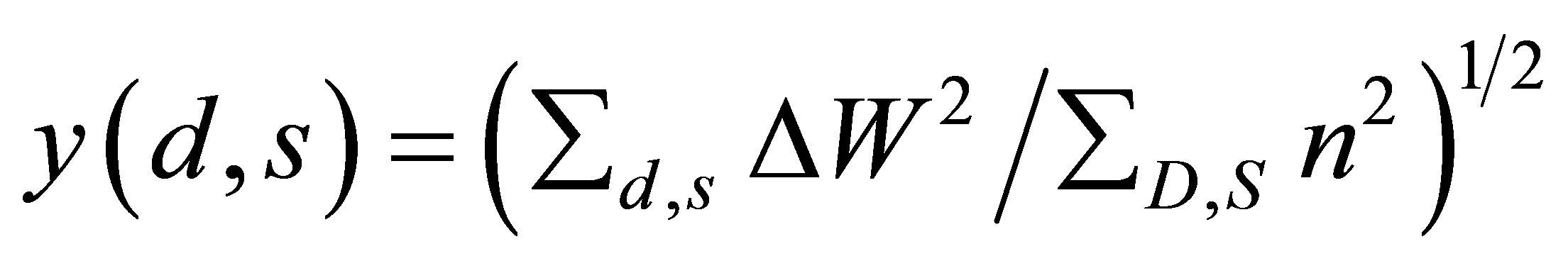 (9)
(9)
and
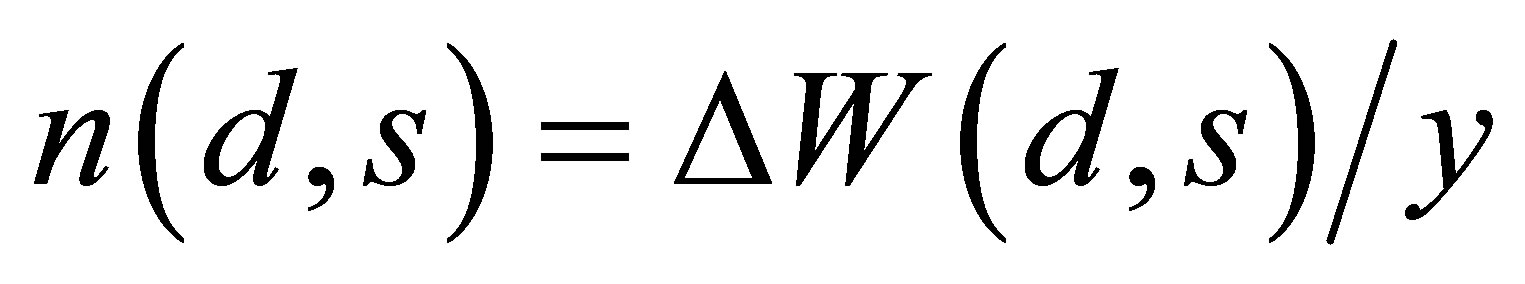 (10)
(10)
All of the known masses of the charged fundamental fermions (except t-quark) are summarized in the Table 1.
Here we find the values of W and ΔW calculated by Formulas (1) and (6). The values of n for d and s (as for u and c) are calculated from the expression (10). The angle
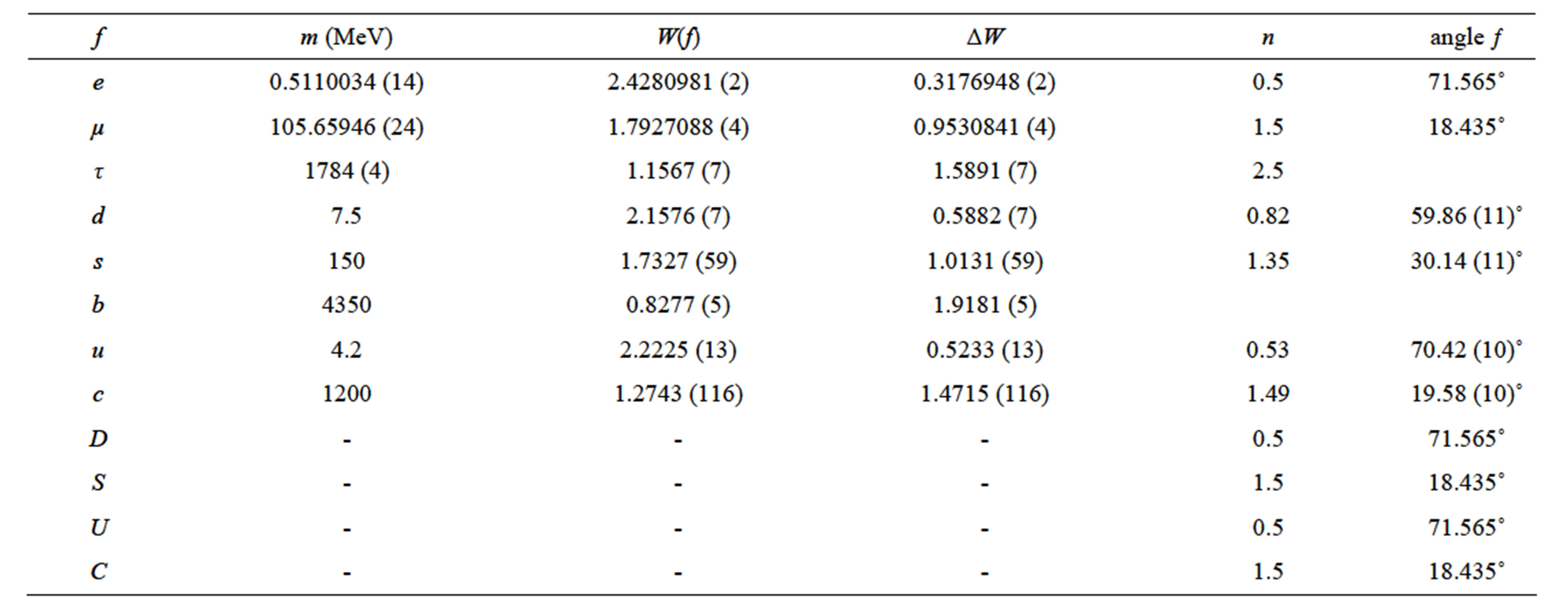
Table 1. Parameters of the charged fundamental fermions.
between the relevant state vector and the line n (Figure 2) is given in the last column. Quite naturally, the state e, D and U vectors with the same value of n = 0.5 have the same angles of slope to the axis n (ƒ = 71.565°). The same is true of the state μ, S and C vectors with n = 1.5 (ƒ = 18.435°).
For quarks in the calculation it is assumed that their masses are in the range: Table 1 value [1] plus or minus 5 in the position, following the last significant digit. For example, m(d) = 7.45 - 7.55 MeV, m(s) = 145 - 155 MeV (the use of modern values of quark masses does not lead to any significant change in the results, which is not surprising, taking into account double logarithmic dependence of W on m).
According to the Table 1, it is easy to determine the mixing angle of bottom quarks: f(D − d) = f(D) − f(d) = 11.70 (11)°. Somewhat surprisingly, this value is slightly less than the conventional value of the Cabibbo angle. But what is really surprising is that, according to the data in the same table, a similar situation also exists for the upper quarks: they also have the rotated states and, consequently, their own mixing angle f(U − u) = ((f(U) − f(u)) = 1.14 (10)°. And the sum of the two angles is practically equal to the known value of Cabibbo angle.
Why is it generally accepted that bottom quarks rotate and the top quarks do not? In [1] the following answer is given: “it is enough to rotate either d and s quarks, or u and c quarks; simultaneous rotation of both does not lead to any new observable phenomena, as the expression for the charged current depends only on the difference between the angles of these rotations”. However, the fact that the parameters of mixing bottom quarks are explicitly expressed in terms of their mass, leads to the conclusion that the bottom quarks are obviously rotating. On the other hand, the link between the mixing parameters and the masses should be universal, i.e. it should exist not only for the bottom quarks, but also for other particles. That is why the independent mixing of the top quarks, so unexpectedly discovered, in fact is not so surprising 0˚.
3. Conclusions
Thus, the existence of the functional connection between the masses of bottom quarks and mixing parameters is established. Only taking into consideration such a connection is possible to give a unified description of the dependence of the masses of all charged fermions (except t-quark—single quark, which “born and die being free” [5]) on the generation number. It turns out that the increments of values 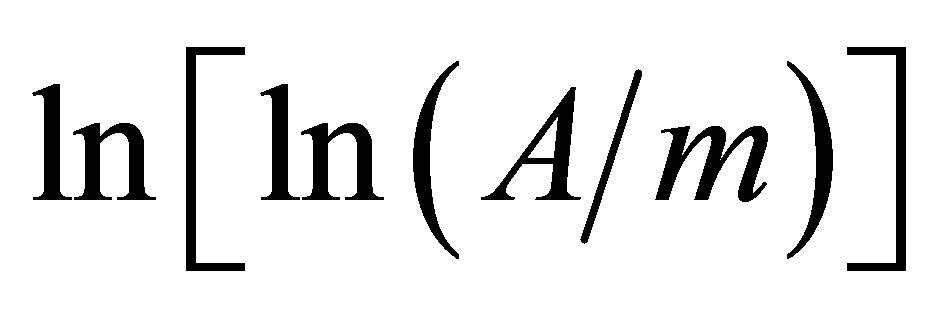 and N are linearly linked.
and N are linearly linked.
It has also been established that the connection between the masses of the quarks and their angle of mixing is universal, i.e., it is not only bottom quarks that are mixing, as it was known up to now, but the top quarks, independently, are mixing too, although to a much lesser extent. Of course, in all experiments with charged currents the value of the angle, equal to the sum of the calculated angles (11.70 (11)˚ + 1.14 (10)˚ = 12.84 (21)˚), is recorded. This value is treated today as the mixing angle of the bottom quarks.
The existence of two independent mixings probably means that the directions of the Higgs bosons in the space of internal symmetry are different for the upper and lower quarks. Therefore, the presence of the two mixings seems to be incompatible with the minimal Higgs model, in which there is only one Higgs boson. Apparently, the more appropriate may be the models with at least two scalar bosons [2,6]. But Higgs mechanism is also responsible for the formation of mass of leptons, at any rate the charged ones. That is why we can assume the existence of not two but a larger number of varieties of Higgs bosons. In this connection, it should be noted that possibly [7] not one but several Higgs bosons were discovered on the LHC.
Of course, there are many questions. How to explain the complete loss of t-quark in the proposed scheme? How to extend this scheme to non-charged leptons? What is the physical meaning of the parameter A? We hope that over time there will be answers.
REFERENCES
- L. B. Okun, “Leptons and Quarks,” Nauka, Moscow, 1990.
- S. V. Troitsky, “Physics-Uspekhi, Vol. 182, 2012.
- M. V. Libanov and E. Y. Nougaev, Journal of High Energy Physics, Vol. 2002, 2002.
- L. S. Sitnikov, “Spectrum of Lepton Masses,” Moscow, 1982. https://sites.google.com/site/leonidsitnikov/spectrum-of-lepton-masses
- L. B. Okun, Physics-Uspekhi, Vol. 41, 1998, pp. 553-557. http://dx.doi.org/10.1070/PU1998v041n06ABEH000403
- K. Grozhan, Physics-Uspekhi, Vol. 177, 2007.
- “There Were a Lot of Higgs Bosons.” http://www.pravda.ru/science/eureka/hypotheses/04-09-2012/1126996-two_higgs-0/

