Journal of Modern Physics
Vol. 4 No. 8A (2013) , Article ID: 36093 , 3 pages DOI:10.4236/jmp.2013.48A008
Doppler’s Effect, Gravity and Cosmology
Central India Research Institute, Nagpur, India
Email: waghsm.ngp@gmail.com
Copyright © 2013 Sanjay M. Wagh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 6, 2013; revised July 13, 2013; accepted August 2, 2013
Keywords: Dopper’s Effect; Implications for Theory of Gravity; Cosmology
ABSTRACT
We first show that Doppler’s effect implies that the time runs identically in the frames of reference of the source of light and the observer. Furthermore, we then show that the frequency shift due to the (assumed) expansion of space, if any, is “indistinguishable” from that due to the motion of the source with respect to the observer; and that the shift does not depend on the distance to the source. Observed frequency shifts of cosmological sources then need to be interpreted as being only due to their motions with respect to us. This has important implications for our ideas in cosmology.
1. Introduction
In 1842, Christian Doppler discovered [1] that whenever a source of light is in motion relative to an observer, the period of the light wave as measured by that observer is different than that it is emitted by the source with. In what follows, we are concerned with the implications of the general explanation of Doppler’s effect, with general- ity of explanation referring here to its applicability for any state of the relative motion of the source and ob- server, whether of uniform velocity or accelerated.
2. Explaining Doppler’s Effect
In its generality, Doppler’s discovery is to be understood [2] as follows. Part (a) of Figure 1 shows a stationary source S of light. Let a light-front reach an observer at O at t = 0. Let observer’s velocity be along OP making an angle θ with OS, as shown. At time t = 0, the light-front immediately following the first one is at point M, which is at distance cT from O. Here, c is the speed of light (in vacuum) and T is the period of the wave emitted by the source. Let the second light-front catch the observer at P along the ray SQP at time T'.
The angle  is tiny when the source S is distant from the observer. Then, MP is good approximation for QP. Thus, we obtain:
is tiny when the source S is distant from the observer. Then, MP is good approximation for QP. Thus, we obtain:
 (1)
(1)
Clearly, only when (OP) = 0 that we have T' = T, that is, the measured period T' of the light wave equals the period T as emitted by the source. Otherwise, the two periods are different, as was Doppler’s discovery.
Moreover, when the observer is moving (away from) (towards) the source we obtain (increase) (decrease) in the measured period T'.
Part (b) of Figure 1 then shows a stationary observer and a source S moving with velocity v along the line SP. From the considerations similar to those of the Part (a) with 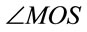 being very tiny, we obtain:
being very tiny, we obtain:
 (2)
(2)
where 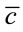 is the speed of light (in vacuum),
is the speed of light (in vacuum), 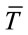 is the period of the wave emitted by the source, and
is the period of the wave emitted by the source, and  is the measured period, all in a new frame of reference.
is the measured period, all in a new frame of reference.
Notice that the observer is shown moving away from the source in Part (a), while the source is shown moving towards the observer in Part (b) of Figure 1; and that accounts for the difference in signs of the cosθ terms of Equations (1) and (2).
Also, notice that we do not have to specify how the observer has traveled distance (OP) in Part (a) or the source has traveled distance (SP) in Part (b) of Figure 1 whether with uniform velocity, uniform acceleration or with variable acceleration.
Furthermore, if Equations (1) and (2) are not identical for (SP) = (OP), the observer will be able to measure self

Figure 1. Geometry of the Doppler effect.
motion using Doppler’s effect. Then, the (general) principle that no observer measures self motion using physical effects requires, in the simplest way, that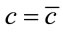 ,
, 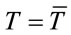 ,
, 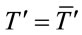 , which we assume, henceforth.
, which we assume, henceforth.
Now, assuming constant acceleration, we may write for distance (OP) as:
 (3)
(3)
where u is the velocity of the observer (source) at t = 0 and v that at time t = T'.
Then, writing  for the measured frequency,
for the measured frequency,  for emitted frequency and using Equation (3) in Equation (1), we obtain a quadratic in
for emitted frequency and using Equation (3) in Equation (1), we obtain a quadratic in  that can be solved to obtain:
that can be solved to obtain:
 (4)
(4)
which yields  when the source and the observer are relatively at rest.
when the source and the observer are relatively at rest.
Now, when the line of motion OP is perpendicular to the line OS, the initial line of sight to the source, we have [3] the transverse Doppler effect as:
 (5)
(5)
Furthermore, when the velocity is uniform, we have:
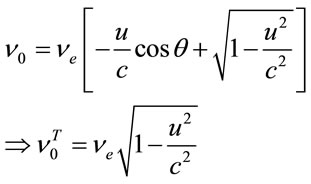 (6)
(6)
The above explanation of Doppler’s effect has following features:
1) It crucially assumes only the constancy of the speed of light for all observers; whether moving with uniform velocity or with uniform or with variable acceleration. Acceleration dependence of the Doppler shift is then an implication of this assumption;
2) The approximation that the distance between the source and the observer is much larger than the wavelength of light is incidental for it;
3) It does not involve the transformation of the time coordinate between the frames of reference: T' or 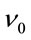 is, and so is T or
is, and so is T or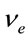 , identical in them. This is required to ensure that the observer does not detect self-motion;
, identical in them. This is required to ensure that the observer does not detect self-motion;
4) Assumed constancy of the acceleration (either of the source or of the observer) should be a good approximation as it is over the period of the light wave.
Then, let us note that Equations (4) through (6) are consistent with all the laboratory experiments [4-6] measuring the Doppler shift.
Notice that, here, the acceleration dependence of the Doppler shift is not an assumption, but an implication of the constancy of the speed of light (in vacuum) for all observers.
An experiment for the acceleration-dependence of the Doppler shift is proposed in [2].
3. Implications for the Theory of Gravity
Now, of importance to our ideas of gravity is the fact that the Doppler effect does not involve the transformation of the time coordinate between the considered two frames of reference. Thus, time runs identically in the two frames of reference, of the source and of the observer, with the following as its immediate implication.
If we consider “space’’ to be expanding (contracting), then also a frequency shift results. This is illustrated in Parts (a) and (b) of Figure 2 using an expanding sphere for the purpose of this illustration.
However, the frequency shift due to the expanding space is, mathematically rigorously, equivalent to the Doppler shift corresponding to appropriate velocity v, of the kind shown in Part (c) of Figure 2, with the “space’’ being Euclidean. That is, Doppler’s effect does not distinguish between the motion of the source/observer (within a Euclidean space) and the expansion of the (assumed curved or not) space.
Notice that the aforementioned is not a necessary conclusion if time runs differently in the frames of reference of the observer and the source of light. In Einstein’s theory of gravity, the expansion of space and the motion of the source influence the frequency differently.
Figure 3 now illustrates Doppler’s effect in a “static’’ curved space, for this illustration as a sphere of radius R. Source S emits waves that travel to the observer at O. As shown, the source then moves to location P on the sphere. Locally, the motion of the source S along the “curve” SP is at an angle θ with respect to the great circle SO. At the observer’s location O, the first wavefront and the wavefront immediately following it are situated in the same manner as shown in Part (b) of Figure 1.
Then, unless the curvature of the space affects the wave propagation over its wavelength, Equations (1) and

Figure 2. Expanding space and the Doppler effect.
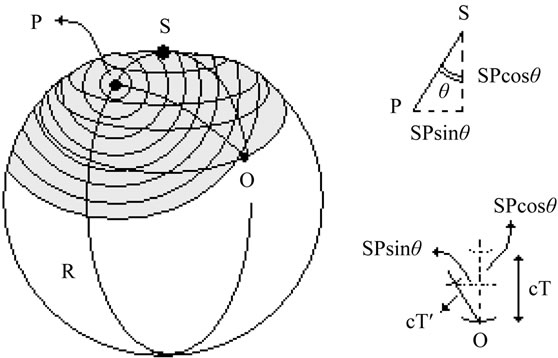
Figure 3. Curved space and the Doppler effect.
(2) hold. Such a strong effect of the curvature of the space is, however, unthinkable for an observer on the Earth. As a consequence, observations of astronomical sources performed at the Earth will obey the formulas that follow from Equations (1) and (2). This will then be the case notwithstanding the situation of the curvature of the space at the location of the source.
Then, the frequency shift does not depend on the distance between the source and the observer even when the space is considered to be curved and expanding. The frequency shift thence depends only on the velocity and the acceleration of the source relative to the observer.
4. Concluding Remarks
From the general explanation of the Doppler effect, the frequency shift is not an indicator of the distance of the source from the observer, but only of its motion relative to that observer.
Of importance is then the fact that the observed frequency shifts of “cosmological” sources do not indicate their distances, therefore.
However, most of the ideas of the present cosmology are based on the red shift being interpreted as an indictor of the distance of a cosmological source.
But, interpreting frequency shift(s) only in terms of the motion(s) of the astronomical source(s) is the only proper interpretation of the frequency shift. Disentangling the effect of the velocity of the source on the frequency shift from that of its acceleration will then be important for our ideas in observational and theoretical cosmology.
REFERENCES
- Relevant Discussion in S. M. Wagh and D. A. Deshpande, “Essentials of Physics,” Vol. 2, Prentice-Hall India, New Delhi, 2013.
- S. M. Wagh, Pramana, 2013, in Press.
- A. Einstein, Annalen der Physik, 1905, p. 17.
- H. E. Ives and G. R. Stilwell, Journal of the Optical Society of America A, Vol. 28, 1938, p. 215. doi:10.1364/JOSA.28.000215
- H. E. Ives and G. R. Stilwell, Journal of the Optical Society of America A, Vol. 31, 1940, p. 369. doi:10.1364/JOSA.31.000369
- D. Hasselkamp, E. Mondry and A. Scharmann, Zeitschrift für Physik, Vol. A289, 1979, p. 151.

