Journal of Modern Physics
Vol.4 No.8(2013), Article ID:35808,8 pages DOI:10.4236/jmp.2013.48146
Quantum Heat Engines; Multiple-State 1D Box System
1Laboratory of Theoretical Physics and Natural Philosophy, Department of Physics, ITS, Surabaya, Indonesia
2Physics Department, State University of Malang, Malang, Indonesia
Email: eny09@mhs.physics.its.ac.id, purwanto@physics.its.ac.id
Copyright © 2013 Eny Latifah, Agus Purwanto. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 20, 2013; revised June 21, 2013; accepted August 1, 2013
Keywords: Quantum Heat Engine; Quantum Thermodynamic Processes; Quantum First Law of Thermodynamic
ABSTRACT
We evaluate quantum Otto, Diesel and Brayton cycles employing multiple-state 1D box system instead of ideal gas filled cylinder. The work and heat are extracted using the change in the expectation of Hamiltonian of the system which leads to the first law of thermodynamics to quantum system. The first law makes available to redefine the force which is in fact not well defined in a quantum mechanical system and then it is applied to define the quantum version of thermodynamic processes, i.e. isobaric, isovolume and adiabatic. As the results, the efficiency of quantum Otto engine depends only on the compression ratio and will be higher than the efficiency of quantum Diesel which can decrease by the widening of expansion under isobaric process. The efficiency of quantum Brayton engine may reach maximum on certain combination between the wide of box under isobaric expansion and compression, under certain conditions. The amount of levels participated in the quantum heat engine system will potentially reduce the performance of the quantum heat cycles consisting isobaric process, but it can be resisted using isobaric process controller.
1. Introduction
Present technology allows for the probing and realization of quantum mechanical systems of mesoscopic and even macroscopic sizes, which can also be restricted to a relatively small number of energy states [1,2]. It is thus important to study these quantum systems directly in relation to the thermodynamics system. The interplay between thermodynamics and quantum physics has been an interesting research topic since 1950s [3,4]. Studies of quantum thermodynamics not only promise important potential applications in technology and quantum information processing, but also bring new insights into some fundamental problems of thermodynamics, such as Maxwell’s demon and the universality of the second law [1,2,4,5]. Among all the studies about quantum thermodynamics, a central concern is to make quantum mechanical extension of classical thermodynamic processes and cycles of quantum heat engines [5-9].
Quantum heat engines produce work using quantum matter as their working substance. The principle conceptual difference between these and conventional heat engine is that in the quantum heat engine one is concerned with the discrete energy levels of particle [8]. Very recently considerable progress has been made in understanding foundational aspects of thermodynamics by addressing a new class of questions: whether there exist additional fundamental limitations on thermal machines, arising specifically due to their size [10,11]. Further, the exotic properties of quantum nature of a working substance can be expected to surpass the maximum limit on the amount of work done by a classical thermodynamics cycle and then improves the efficiency [12-15].
Some studies on quantum heat engine focused on the quantum analogue of classical Carnot engine [6,7]. The quantum Carnot engine, employing a single quantummechanical particle, as a working substance, is confined to a 1D box potential instead of gas filled cylinder. The cycle consists of isothermal and adiabatic quantum processes that are close analogues to the corresponding classical processes. By formulating 2-state quantum system, the efficiency is analogue for the classical Carnot efficiency [6]. The study of n-state of 1D box quantum Carnot engine has explored a phenomenon that the efficiency will be looser as an adding of the number of eigen-states included, but it is possible to resist the loss of efficiency by controlling the expansion of isothermal process [7]. If there are some difficulties to control the amount of eigen-state involved in the arrangement of the state of system of a quantum heat engine, the effort to resist the decreasing of the efficiency could be done by studying its properties.
It is important to characterize how the behavior other multiple-state 1D box heat engines, that is quantum Otto, Diesel and Brayton engines. There is an interesting thing to Diesel and Brayton cycles, they consist of isobaric process, so we must redefine “pressure” (force), which has not been challenged yet to participate in the previous studies of 1D box system quantum engine [6,7,16] and is in fact not well defined in a quantum mechanical system [3,17].
In this paper, as an attempt to have an overview of 1D system of quantum heat engines, we evaluate quantum Otto, Diesel and Brayton engines which classically have an ideal gas as their working substance. Different from the previous papers according to quantum Carnot engine 1D system [6,7] and Otto like cycle for a two-level system [18], here we evaluate the multiple-state 1D system heat engines using the first law of thermodynamic to quantum system defined from statistical interpretation of measurement energy in quantum mechanics. By the first law, the force in the quantum mechanical system can be redefined phenomenologically and some thermodynamic processes, i.e. adiabatic, isobaric and isochoric, to 1D box system can be described well. This paper is organized as follows: In Section 2, we redefined microscopically force for a quantum system through the quantum version of the first law of thermodynamic, and we apply the force and the first law to describe the quantum version of quantum version of adiabatic, isobaric and isovolume processes; In Section 3, we evaluate the quantum Otto, Diesel and Brayton engine, formulate their efficiencies and correspond between them. Section 4 contains the remarks and conclusions.
2. The First Law of Thermodynamics to Quantum System
2.1. 1D Box System
We choose a quantum heat engines system, multiplestate 1D box system instead of ideal gas filled cylinder. 1D case is an interesting object which quantum mechanics textbooks usually start with them to illustrate some non-classical effects of the theory. The simplest onedimensional quantum mechanical system is a particle of mass m in region with potential is zero along L and otherwise is infinite [19]. The Schrodinger Equation is given
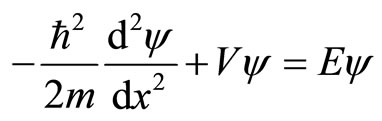 . (1)
. (1)
The potential energy that touches the walls is infinite and  in
in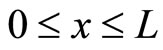 . The infiniteness potential ensures the particle cannot in fact penetrate them and gives the boundary conditions
. The infiniteness potential ensures the particle cannot in fact penetrate them and gives the boundary conditions .
.
The boundary conditions and normalization requirement give us the discrete spectrum of eigenfunctions,
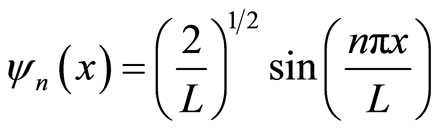 . (2)
. (2)
These eigenfunctions are associated with the eigenenergies
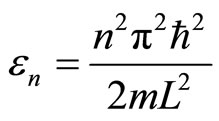 . (3)
. (3)
The state of system, described by a wave function , may be expanded in terms of an eigenfunctions set
, may be expanded in terms of an eigenfunctions set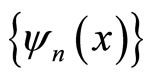 ,
,
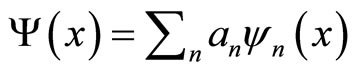 , (4)
, (4)
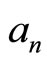 can be called as coefficient expansion. If the states
can be called as coefficient expansion. If the states  and
and 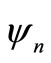 are normalized, the coefficients will have the normalization correction
are normalized, the coefficients will have the normalization correction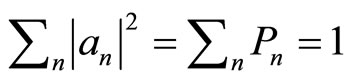 .
.
The quantum mechanical prescription for calculating the average of a dynamical observable in the state 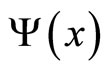 is written in the postulates. Specifically, for the energy we have the expectation value of Hamiltonian. If the probability to finding
is written in the postulates. Specifically, for the energy we have the expectation value of Hamiltonian. If the probability to finding  in a given measurement of energy is
in a given measurement of energy is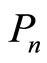 , then the average energy over measurements in the box is given by the expression
, then the average energy over measurements in the box is given by the expression
 . (5)
. (5)
Here we have the interpretation of the square of modulus of coefficient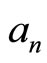 ,
, 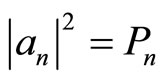 is the probability that measuring energy finds the value
is the probability that measuring energy finds the value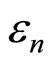 . So the energy of 1D system is
. So the energy of 1D system is
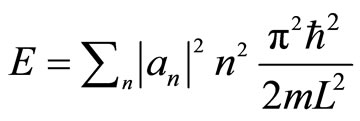 . (6)
. (6)
Here we assume, one of the walls, say the wall at x = L, is allowed to move an infinitesimal amount dL then the wave function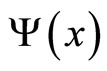 , eigenfunctions
, eigenfunctions 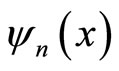 and eigenenergies
and eigenenergies 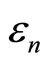 all can vary infinitesimally as function of L. As a consequence, the expectation value of Hamiltonian, Equation (6) also changes infinitesimally.
all can vary infinitesimally as function of L. As a consequence, the expectation value of Hamiltonian, Equation (6) also changes infinitesimally.
2.2. The First Law of Thermodynamics, Force and Energy to Quantum System
Force, in which has not been challenged in the previous studies of 1D box system quantum engine [6,7,17], is in fact not well defined in a quantum mechanical system [3,16]. Here, we redefine the force and energies of the system based on the phenomenological interpretation of the infinitesimally changing of the expectation value of Hamiltonian.
The expectation value of Hamiltonian is the average energy over measurements of all members of the ensemble, it can be just called as the energy of the system. Under an infinitesimal process, the infinitesimally changes in the energy of Equation (5) are given by
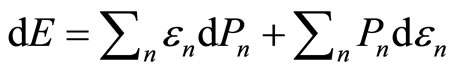 . (7)
. (7)
It is the statement of the first law of thermodynamic to quantum mechanical systems [1-3,16]. The two terms of Equation (7) tell us that there exist two fundamentally different ways of change of the energy of system. The first term represents the change of state occupation or probability 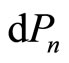 and the second term gives the change of energy levels
and the second term gives the change of energy levels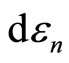 .
.
We evaluate this two terms phenomenologically. At first, under an adiabatic process, the adiabatic theorem is invoked to obtain that energy levels are modified without changing their occupational probability [20], 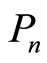 is invariant. The first law in Equation (7) will be
is invariant. The first law in Equation (7) will be
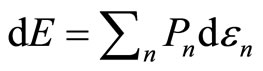 . (8)
. (8)
While classically, this no heat transfer process of adiabatic process will lead to use the change of internal energy only to do work . According to 1D box, the volume decreases slowly from L to L-dL by application of an external force, so
. According to 1D box, the volume decreases slowly from L to L-dL by application of an external force, so
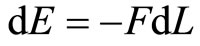 . (9)
. (9)
Substitusion of Equation (8) into Equation (9) gives us the ensemble average of force,
 . (10)
. (10)
The ensemble average of force F is the average of  over all the states represented in the ensemble [15]. It appears to introduce the macroscopic observable quantity of force or “pressure”, i.e., as a function of the microstate. Let amount of heat
over all the states represented in the ensemble [15]. It appears to introduce the macroscopic observable quantity of force or “pressure”, i.e., as a function of the microstate. Let amount of heat 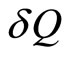 can be supplied to the system, and the system does an amount of work
can be supplied to the system, and the system does an amount of work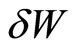 . By the principle of conservation energy, the infinitesimal change of the (internal) energy is then given by the first law as,
. By the principle of conservation energy, the infinitesimal change of the (internal) energy is then given by the first law as,
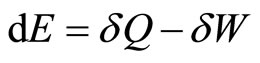 . (11)
. (11)
This change of energy 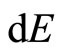 has also been given in Equation (7). It has been defined previously the change of energy levels
has also been given in Equation (7). It has been defined previously the change of energy levels 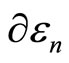 can be with the infinitesimally moving of the wall
can be with the infinitesimally moving of the wall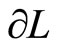 , the term
, the term 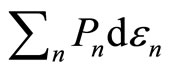 will be related to the work done to the system. In other hand, the rearrangement of the system among the energy levelswhich lead to
will be related to the work done to the system. In other hand, the rearrangement of the system among the energy levelswhich lead to 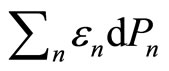 term, must therefore be related to the head supplied into the system,
term, must therefore be related to the head supplied into the system,
 . (12)
. (12)
The situation has also defined been formally using quantum manometer model [16] which has results that the first (term) process of Equation (7) requires an explicit thermodynamic embedding, and the second (term) process has been shown to require what could be called a mechanical embedding.
2.3. Quantum Version of Thermodynamics Processes
Base on the force and the first law of thermodynamics to a quantum mechanics system, we can now describe some processes which are quantum analogues of classical thermodynamic processes.
2.3.1. Adiabatic Process
A classical adiabatic process can be formulated in terms of a microscopic quantum adiabatic process. Because quantum adiabatic processes proceed low enough such that the generic quantum adiabatic condition is satisfied, then the population distributions remain unchanged. There is no heat exchange in the process, but work can still be nonzero according to equation. A classical adiabatic process, however, does not necessarily require the occupation probabilities to be kept invariant. For example, when the process proceeds very fast, and the quantum adiabatic condition is not satisfied, internal excitations will likely occur, but there is no heat exchange between the working substance and the external heat bath. This thermodynamics process is classical adiabatic but not quantum adiabatic [7]. Thus it can be verified that a classical adiabatic process includes, as a subset, a quantum adiabatic process; but the inverse is not valid [6].
In case, the internal energy is converted all into mechanical energy, the first law will be,
 . (13)
. (13)
We use an assumption that the initial state of the system is a linear combination of n-eigen-states as stated in Equation (4). In this process, the size of the potential well changes as the moving wall moves. There is no transition between energy levels, it can be represented the absolute values of the expansion coefficient  is invariant. Using adiabatic process we can construct the force as,
is invariant. Using adiabatic process we can construct the force as,
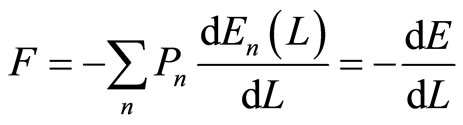 (14)
(14)
Equation (14) has been well used in the previous quantum Carnot engine 1D system [6,7]. This expression of force  is not a general expression of force according to quantum system, it is just special cases according to adiabatic and isothermal processes, and will be only well used for Carnot cycle [6,7].
is not a general expression of force according to quantum system, it is just special cases according to adiabatic and isothermal processes, and will be only well used for Carnot cycle [6,7].
The eigen-states 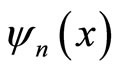 and the corresponding energy levels En, as the wall moves an infinitesimal amount dL, will be varying smoothly. Energy level does not independent to the wide of wall L, as described in Figure 1.
and the corresponding energy levels En, as the wall moves an infinitesimal amount dL, will be varying smoothly. Energy level does not independent to the wide of wall L, as described in Figure 1.
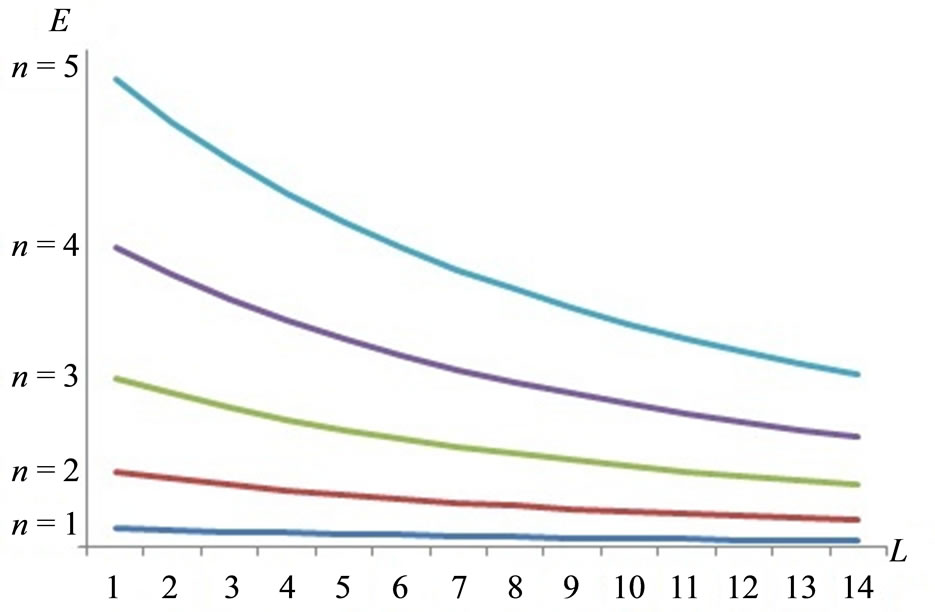
Figure 1. Under an adiabatic process, the energy levels and energy levels spacing decrease as the wall moves out.
Each eigenvalue of energy En decreases as the piston moves out, so from Equations (3) and (5) we have the expectation value of Hamiltonian decreases as
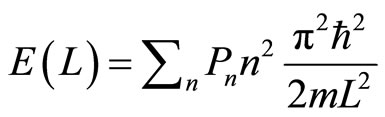 . (15)
. (15)
The force exerted to the moving walls by the system, as stated in Equation (14) is given by
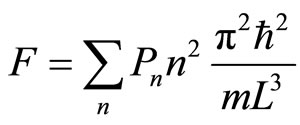 , (16)
, (16)
in accordance with the formulation as shown in Equation (10).
2.3.2. Isobaric Process
Many energy transfer processes are taken place in close system at constant pressure. These processes are said to be an isobaric process. In contact with a heat bath, the first law of thermodynamics is stated in Equation (7) as . The amount of heat input can be predicted with
. The amount of heat input can be predicted with
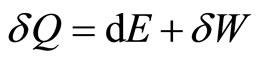 , (17)
, (17)
which is used to change the internal energy and to do work under a constant force.
According to 1D system, the quantity of pressure is played by force, so the force remains constant along the isobaric expansion or compression processes,
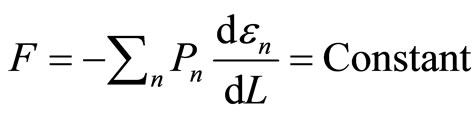 . (18)
. (18)
Let us assume, initially, the system is in ground state,  , and appropriates with the force
, and appropriates with the force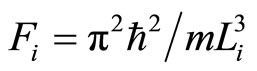 . The heat input blows transitions between states, so the force will be
. The heat input blows transitions between states, so the force will be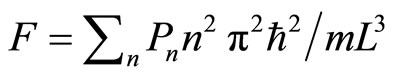 . This constant force, isobaric, gives us information of the wide of wall after isobaric expansion or compression
. This constant force, isobaric, gives us information of the wide of wall after isobaric expansion or compression
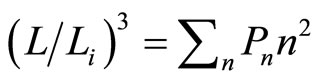 , (19)
, (19)
which will be maximum when all of the eigen-states lay on the highest state, or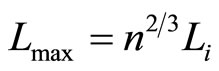 .
.
2.3.3. Isovolume Process
In an isovolume process, the system is placed in contact with a heat bath. Classically, the pressure p and the temperature T are changing along this process. The constant volume assures no work along the process.
A quantum isovolume process has similar properties to that of a classical isovolume process. The occupation probabilities vary along a quantum isovolume process by the heat absorbed or released. The system changes at constant volume, dL = 0 (for 1D system), thus no work is done by or into the system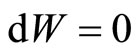 . The heat input all will be used to raise the energy of the system so the first law can be stated as,
. The heat input all will be used to raise the energy of the system so the first law can be stated as,
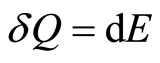 . (20)
. (20)
The internal energy goes up by the heat added into the system.
3. Quantum Heat Engine
To study the conversion of heat into work, we must have at hand a process, or series of processes, by means of which such a conversion may continue indefinitely without involving any resulting changes in the state of the system. The series of processes in which a system is brought back to its initial state, that is, a cycle. Each of the processes that constitute a cycle involves either the performance of work or a flow of heat between the system and its surroundings, which consist of a heat reservoir at a higher temperature than the system and a heat reservoir at a lower temperature than the system [14]. Cyclic heat engines play an extraordinarily large role in technique. A large part of the energy used in daily life is produced in such engines, for example in nuclear power plants, or combustion engines [15].
Starting with a ground-state of 1D system of width L1, the state is
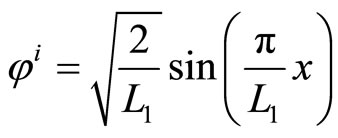 . (21)
. (21)
It associates with the energy,
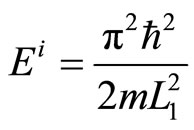 . (22)
. (22)
The initial state and energy Equations (21) and (22) will be changed quasistatically to go through the quantum cycles returning to these state and energy.
In the following study, we apply the quantum version of the first law, force, energy and thermodynamic processes which have been defined in the section 2 to evaluate the behavior of quantum Otto, Diesel and Brayton cycles and formulate their efficiencies. We consider a case of system with n-eigen-states contributed to the wave function in the 1D box.
3.1. Quantum Otto Cycle
Otto engine is sequentially made up adiabatic compression, isovolume, adiabatic expansion and return to its initial state after undergoing the isovolume.
1D box quantum Otto engine operates under a cycle which is a quantum mechanical analogue to the classical Otto cycle [14,15,21,22]. Figure 2 shows the 1D quantum Otto cycle on FL diagram. At first, the wall is compressed adiabatically , the occupation probabilities remain constant. Amount of heat
, the occupation probabilities remain constant. Amount of heat 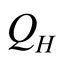 inputs into the system, raising the energy and makes change in the occupation probability and the force goes up while the volume doesn’t change. Next the high force of the system pushes the wall outward
inputs into the system, raising the energy and makes change in the occupation probability and the force goes up while the volume doesn’t change. Next the high force of the system pushes the wall outward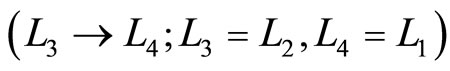 , expanding adiabatically and producing the work. Finally, amount of heat called
, expanding adiabatically and producing the work. Finally, amount of heat called 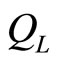 is expelled under isovolume process and the system gets a lowering force, the system expels heat but does not do work until achieves its initial condition (Equations (23) and (24)).
is expelled under isovolume process and the system gets a lowering force, the system expels heat but does not do work until achieves its initial condition (Equations (23) and (24)).
The net work for a cycle is stated as,
 . (23)
. (23)
According to Otto cycle, the net work is rendered by the quantum adiabatic compression and adiabatic expansion
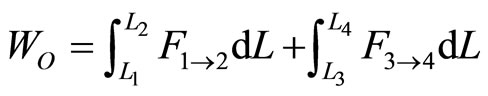 . (24)
. (24)
Substitution Equation (18) into Equation (24) gives us the expression of the Otto cycle net work,
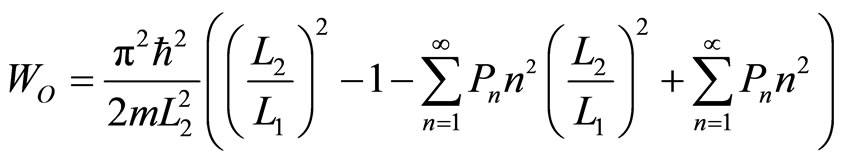 . (25)
. (25)
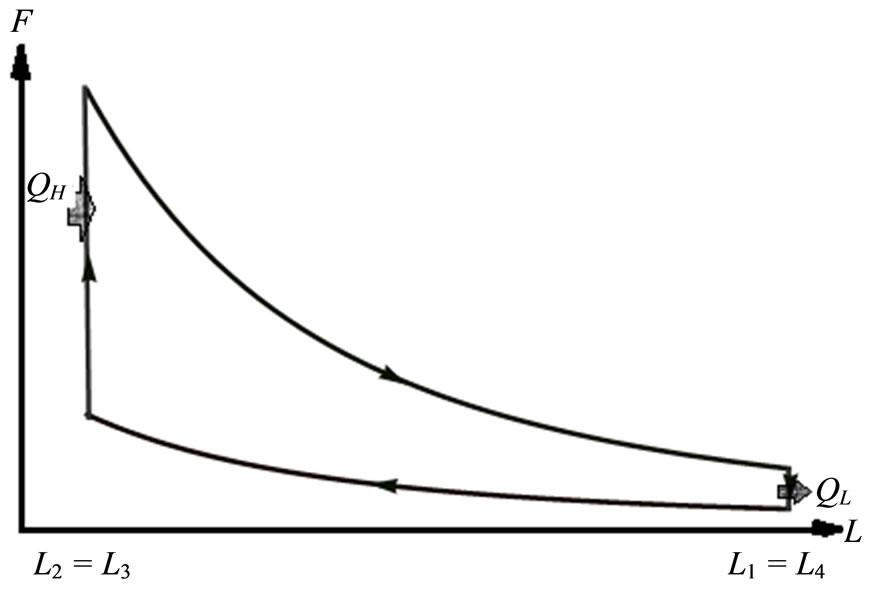
Figure 2. FL diagram 1D box Otto cycle.
The width of 1D box parameter does not vary when the system is in contact with either bath. The parameter varies only during the adiabatic transitions from one bath to the other bath. This cycle may deliver work or receive work for appropriate choice of the parameters.
The heat inputs at a constant volume , and it can be obtained by the first law (Equation (20)),
, and it can be obtained by the first law (Equation (20)),
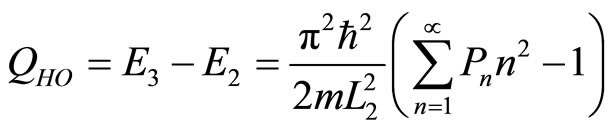 . (26)
. (26)
The efficiency of this quantum Otto engine is the net work producer during the cycle, Equation (25) divided by the heat absorbed during the isovolume of process  Equation (26). Using Equations (25) and (26), we have
Equation (26). Using Equations (25) and (26), we have
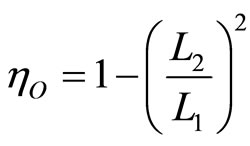 , (27)
, (27)
where 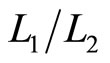 is the compression ratio. We can therefore eliminate the compression in Equation (27) in favor of the energy of system at the ends of either adiabatic process,
is the compression ratio. We can therefore eliminate the compression in Equation (27) in favor of the energy of system at the ends of either adiabatic process,
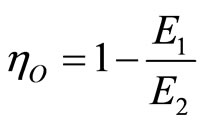 . (28)
. (28)
The obvious way to make the efficiency more efficient would be to use a higher compression ratio. This result corresponds to the classical Otto efficiency which is determined as a temperature ratio of the cold and hot baths 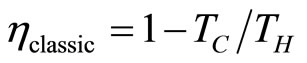 [19].
[19].
3.2. Quantum Diesel Cycle
A Diesel cycle is constructed out of an adiabatic compression and an adiabatic expansion interspersed between an isobaric compression and isovolume. The 1D box system quantum diesel cycle analogue to its classical cycle can be described in FL diagram of Figure 3. Heat flows into the cycle through the expansion under constant force and it flows back out through the isovolume process.
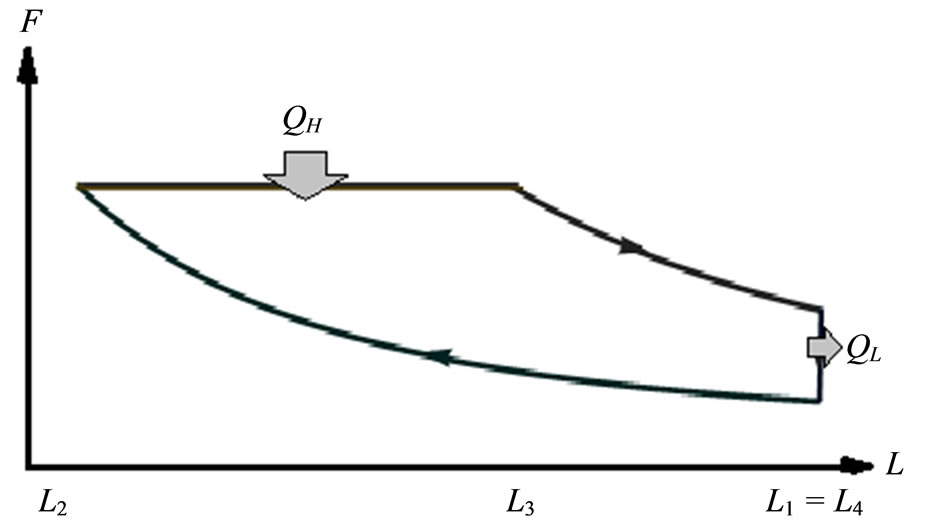
Figure 3. FL diagram of 1D box Diesel cycle.
Applying the first law to the closed system to each of the cycle yields the net work
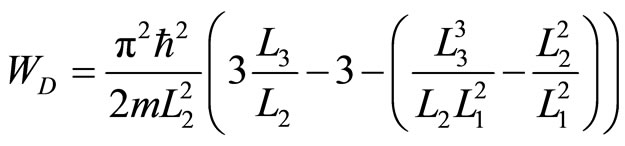 . (29)
. (29)
The amount of heat taken in the system at constant force during process  as given by the first law, Equation (19), is
as given by the first law, Equation (19), is
 (30)
(30)
The diesel efficiency can be obtained from Equations (29) and (30),
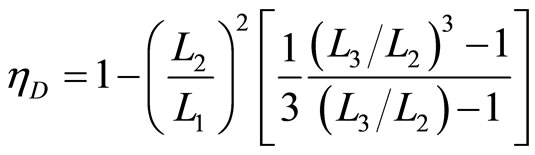 . (31)
. (31)
Equation (31) can be expressed as
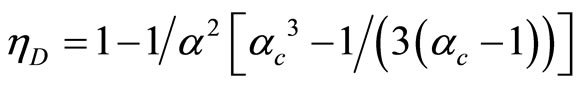
where 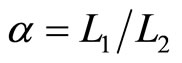 is compression ratio and
is compression ratio and 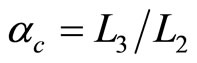 is cut-off ratio. The efficiency of quantum Diesel engine decreases by the larger of cut off ratio [23]. When,
is cut-off ratio. The efficiency of quantum Diesel engine decreases by the larger of cut off ratio [23]. When, 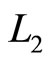 constant, the decreasing of efficiency by the widening of the wall under isobaric expansion can be shown in Figure 4.
constant, the decreasing of efficiency by the widening of the wall under isobaric expansion can be shown in Figure 4.
Our multiple-state system apprises a special character under isobaric process contacting with a reservoir. It is expressed in Equation (21), more eigen-states constructing the state of system, the wall could be dilated more and the cut off ratio will go up. The increasing of cut-off ratio will tend to decrease the efficiency.
A comparison of Diesel efficiency 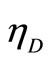 and Otto efficiency
and Otto efficiency 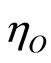 shows that operating at the same compression ratio the Diesel efficiency, Equation (31), is always
shows that operating at the same compression ratio the Diesel efficiency, Equation (31), is always

Figure 4. The Diesel efficiency will decrease by the increasing of the isobaric expansion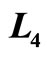 , on the constant of
, on the constant of 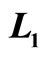 and
and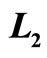 .
.
less than Otto cycle, Equation (27), because the square bracket factor of Equation (31) is always larger than one. This Diesel efficiency will be as close to the quantum Otto efficiency as desired by making the cut off ratio close to one.
3.3. Quantum Brayton Cycle
Brayton engine is constructed with adiabatic compression, isobaric expansion, adiabatic expansion and isobaric compression. The adiabatic processes, as in thermodynamics, are impermeable to heat; heat flows into the loop through the left expanding isobaric process and some of it flows back out through the isovolume process for Brayton. The 1D system Brayton cycle is described in Figure 5.
The force and energy in all stages of the cycle give us the total work,
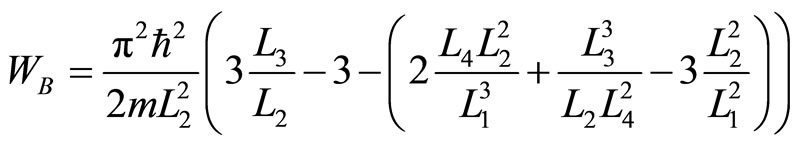 . (32)
. (32)
While, the heat transfered into the system using the first law can be obtained with,
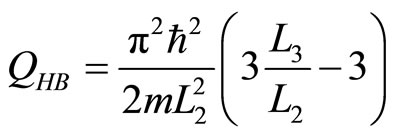 . (33)
. (33)
Then we have the efficiency of the quantum Brayton in
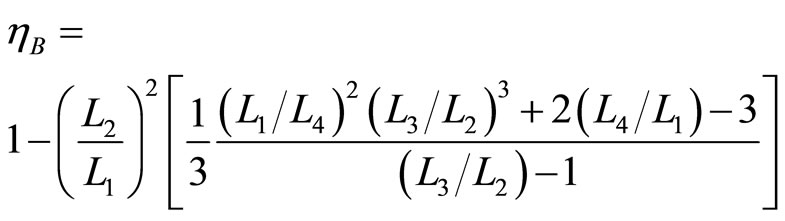 . (34)
. (34)
The efficiency of quantum Brayton engine varies on the compression ratio, and the both of expansion and compression box under isobaric processes. For fixed values of the compression ratio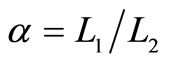 , the behavior of quantum Brayton efficiency can be shown by Figure 6. It reaches maximum on certain combination between the wide of box under isobaric expansion
, the behavior of quantum Brayton efficiency can be shown by Figure 6. It reaches maximum on certain combination between the wide of box under isobaric expansion and adiabatic expansion
and adiabatic expansion . In order to form a cycle process, the ratio
. In order to form a cycle process, the ratio
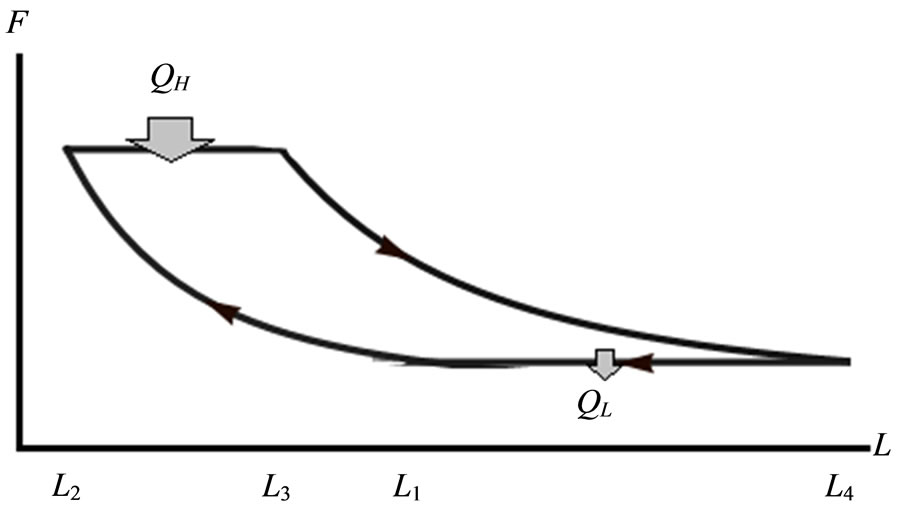
Figure 5. FL diagram of 1D box Brayton cycle.
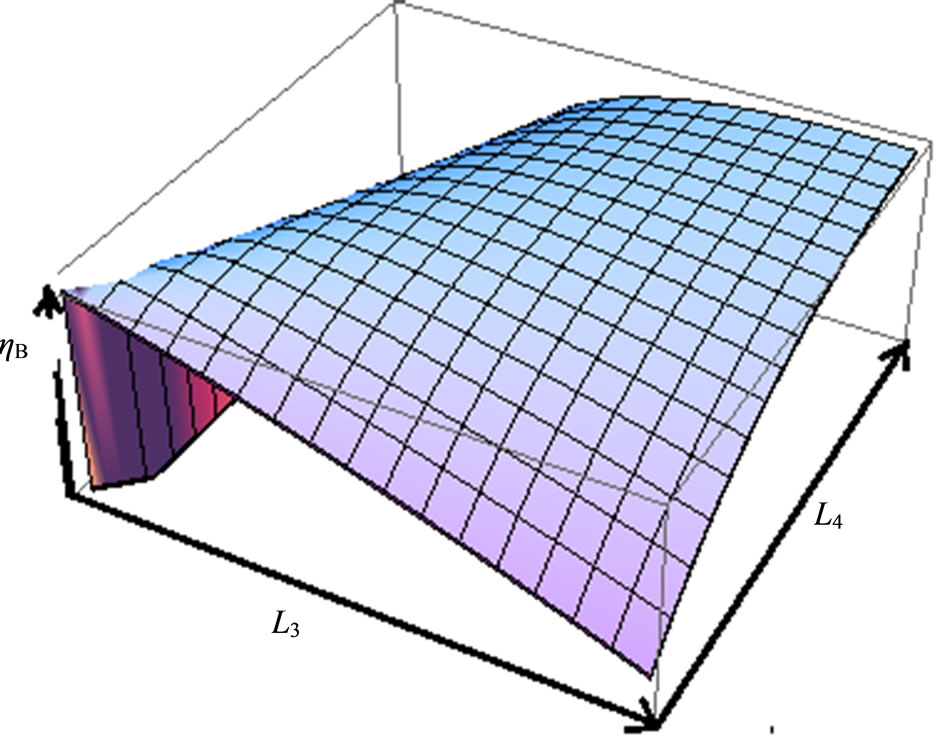
Figure 6. The efficiency of quantum Brayton engine reaches maximum on certain combination of 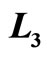 and
and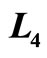 , on the constant of
, on the constant of 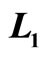 and
and .
.
of isobaric compression 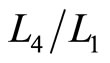 relates to the probability along isobaric expansion process, as stated in Equation (19),
relates to the probability along isobaric expansion process, as stated in Equation (19),
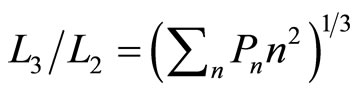 . (35)
. (35)
The amount of levels participated in multiple-state quantum system potentially reduces the performance of our quantum Brayton engine, but it can be resisted using isobaric process controlling.
4. Conclusions and Remark
It has been shown that the efficiencies of 1D quantum heat engines are similar with classical ideal gas heat engines using the expectation value of Hamiltonian, an ensemble average taken over the multiple copies of the system, as the temperature, actually can be measured in energy units [24]. The multiple-state 1D box quantum Otto engine efficiency depends on the compression ratio which is the initial and final internal energy ratio of adiabatic compression. The quantum Diesel efficiency depends on the compression ratio and cut off ratio. It will decrease by the increasing of the cut off ratio which is 1D box elongation ratio under isobaric expansion. Operating at the same compression ratio, the Diesel efficiency is always less than Otto cycle. The work of 1D Brayton engine can be looser not only by elongation under isobaric expansion but also by the contraction of isobaric compression. Operating at the same compression ratio, the quantum Brayton efficiency will be less than Otto and Diesel cycle.
The multiple-state quantum heat engines behave that more eigen-states of the state will reduce the performance of the quantum heat engine. This result presents a confirmation that for the higher state quantum heat engine the work to be looser than that for lower sate system under certain condition [7,9]. The more eigen-states participated in the state can increase the isobaric expansion and vice versa for isobaric compression and it will decrease the efficiency. A controlling of isobaric processes should be done in order to achieve a maximum work, because the system must be brought to execute a reversible cyclic process.
The efficiency enhancement of our multiple-state quantum heat engines can be done by increasing compression ratio and controlling isobaric processes.
5. Acknowledgements
We would like to acknowledge M. F. Rasyid and W. S. Brams D. for their comments on our presentations in Conference on theoretical Physics and Non Linear Phenomena, UGM, Yogyakarta, Sepetember 2012 and Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA, Yogyakarta, Indonesia, June 2012. We would also like to thank to the encouragement of Institut Teknologi Sepuluh Nopember, ITS, via Laboratory of Theoretical Physics and Natural Philosophy (LaFTIFA).
REFERENCES
- T. D. Kieu, “Quantum Heat Engine, the Second Law and Maxwell’s Daemon,” arXiv:quant-ph/0311157v5.
- T. D. Kieu, Physical Review Letters, Vol. 93, 2004, Article ID: 140403
- H. T. Quan, Physical Review E, Vol. 79, 2009, Article ID: 041129. doi:10.1103/PhysRevE.79.041129
- H. E. D. Scovil and E. O. Schulz-DuBois, Physical Review Letters, Vol. 2, 1959, pp. 262-263. doi:10.1103/PhysRevLett.2.262
- H. T. Quan, Y. D. Wang, Y.-X. Liu, C. P. Sun and F. Nori, Physical Review Letter, Vol. 97, 2006, Article ID: 180402.
- C. M. Bender, D. C. Broody and B. K. Meisner, Journal of Physics, Vol. 33, 2000, p. 4427.
- E. Latifah and A. Purwanto, Journal of Modern Physics, Vol. 2, 2011, pp. 1366-1372. doi:10.4236/jmp.2011.211169
- H. T. Quan, Y.-X., Liu, C. P. Sun and F. Nori, Physical Review E, Vol. 76, No. 3, 2007, Article ID: 031105. doi:10.1103/PhysRevE.76.031105
- H. T. Quan, P. Zhang and C. P. Sun, Physical Review E, Vol. 72, 2005, Article ID: 056110.
- G. Mahler, Physics, Vol. 5, 2012. doi:10.1103/Physics.5.55
- N. Linden, S. Popescu and P Skrzypczyk, “The Smallest Possible Heat Engine,” 2010, arXiv:1010.6029v1 [quantph] 28.
- R. Dillenschneider and E. Lutz, “Improving Quantum Carnot Engine with Quantum Correlation,” 2008, arXiv: 0803.4067v1.
- M. O. Scully, Physical Review Letter, Vol. 88, 2002, Article ID: 050602.
- M. W. Zemansky and R. H. Dittman, “Heat and Thermodynamics,” 7 Edition, The McGraw-Hill Companies, Inc., Boston, 1997.
- C. Kittel and H. Kroemer, “Thermal Physics,” W. H. Freedman and Company, 1980.
- C. M. Bender, D. C. Brody and B. K. Meister, Proceedings of the Royal Society, Vol. 458, 2002, pp. 1519-1526. doi:10.1098/rspa.2001.0928
- P. Borowski, J. Gammer and G. Mahler, EPL (Europhysics Letters), Vol. 62, 2003, p. 629. doi:10.1209/epl/i2003-00420-8
- G. P. Baretta, “Quantum Thermodynamis Carnot and OttoLike Cycles for Two-Level System,” 2008, arXiv:quantum-ph/070326v1.
- A. Purwanto and E. Latifah, Open Journal of Microphysics, Vol. 2, 2012, pp. 13-18, doi:10.4236/ojm.2012.22002
- W. O. De Galway and J. Naudts, “Quantum Cooling by Unitary Transformation,” 2011, arXiv:1112.1557v1 [mathph].
- D. V. Schroeder, “An Introduction to Thermal Physics,” Addison Wesley Longman, 2000.
- E. Latifah and A. Purwanto, “Multiple-StateQuantum Otto Engine, 1D Box System,” AIP Conference Proceedings of the 4th International Conference on Mathematics and Natural Sciences (ICMNS), Bandung, 8-9 November 2012.
- E. Latifah and A. Purwanto, “Quantum Mechanical Ideal Diesel Engine,” Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA, Fakultas MIPA, Universitas Negeri Yogyakarta, 2012.
- L. D. Landau and E. M. Lifshitz, “Statistical Physics, Part 1,” 3rd Edition, Pergamon Press, 1980.

