Journal of Modern Physics
Vol.04 No.09(2013), Article ID:36942,6 pages
10.4236/jmp.2013.49162
Particle Horizons in Cosmology
K. Purnachandra Rao
School of Mathematical and Statistical Sciences, Hawassa University, Hawassa, Ethiopia
Email: drkpraocecc@yahoo.co.in
Copyright © 2013 K. Purnachandra Rao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received May 9, 2013; revised June 15, 2013; accepted July 13, 2013
ABSTRACT
The importance of investigating particle horizons in order to interpret a cosmological solution of Einstein’s field equa- tions has been described. We have presented the formula and studied the particle horizons in some of the cosmological models presented in our earlier papers. It is well known that the Friedman-Robertson-Walker (F-R-W) models, the en- ergy density of the free gravitational field denoted by ε, equivalently denoted by MacCallum parameter ξ, vanishes but the particle horizons exist and thus the former has no bearing on the latter. However, we have shown in our models pre- sented herein that ε is related with particle horizons. Further, it is shown that as ε grows, the segment of the correspond- ing particle horizon decreases and thus the radius of the corresponding visible universe decreases.
Keywords:
In Homogeneity; Anisotropy; Cosmology; Particle Horizon
1. Introduction
Cosmology deals with the large scale structure of the universe, which by definition contains everything, viz., both observable and non observable. To understand the physical nature of the universe as a whole, attempts were made during 19th century within the frame work of the Newtonian theory of gravitation. But, these efforts did not fructify since Newtonian gravitation assumed instan- taneous propagation of gravitational interaction for which there had not been any experimental justification.
The progress of modern cosmology has been guided by both theoretical and observational advances. The sub- ject really took off in 1917 with the first cosmological solution given by Albert Einstein based on his general theory of relativity or theory of gravitation. Since then a wide range of cosmological models have been constructed, studied and analyzed with varying objectives.
The Friedman-Robertson-Walker (F-R-W) cosmologi- cal models, derived based on the twin assumptions of spatial isotropy and homogeneity provides a satisfactory description of the observable universe for considerable part of its history. However, the existence of inhomogeneities in the form of galaxies and clusters as well as the anisotropy in the cosmic background radiation could not be explained with the help of these models.
Cosmological models with inhomogeneous density have been studied [1-3]. It has been shown [4-7], that the en- ergy density of the free gravitational field ε is related to
both anisotropy and in homogeneity.
A lot of isotropic and homogeneous cosmological models have appeared in literature but a few models with the characteristics of anisotropy and in homogeneity. An attempt has been made to fill the gap by construction of a wide range of anisotropic and inhomogeneous cosmo- logical models [8-12].
However, in order to interpret a cosmological solution of Einstein’s field equations, one should investigate some special aspects like horizons [13,14]. It has been studied event horizons in cosmology [15]. In the present paper we will describe mathematically and provide graphical representations of particle horizons which exist in some of the models presented in our papers [8-12].
The Eigen value of the conformal Weyl tensor in Pet- rov’s classification [16] is denoted by ε and is known as “the energy density of the free gravitational field” as it always coupled with the material energy density ρ.
In Section 2, following [17,18], we have defined parti- cle horizons and list some properties of the horizons.
In Section 3, we have introduced the most general spherically symmetric space-time metric filled with ani- sotropic fluid. We have given the solutions of Einstein field equations, and expression for the energy density of the free gravitational field represented by ε.
In Section 4, we presented the equations of kinemati- cal quantities, MacCallum quantity ξ, and Raychaudhuri’s equation for the spherically symmetric models.
In Section 5, we have given the formula for particle horizons of the most general spherically symmetric met- ric. We have investigated the existence of particle hori- zons in some of the models discussed in our earlier pa- pers and derived formulae for particle horizons in these models. The diagrammatic representations of the particle horizons studied here have been provided in Figures 1-4. In Section 6, we presented direct comparison between the Event and Particle horizons and graphical representation is provided in Figure 5. In all the figures the radial coor- dinate r is taken along the horizontal axis while the time coordinate t is taken along the vertical axis. The paper ends with concluding remarks in Section 7.
2. Particle Horizons
1) Event horizon
Consider an observer and a photon on its way to the observer along a null geodesic. It can happen that the
Figure 1.Diagrammatic representation of the particle horizon described by (31) of the space-time metric described by (29).
Figure 2. Diagrammatic representation of the particle horizon described by (33) of the space-time metric described by (32).
Figure 3.Diagram showing the particle horizons described by (38) of the space-time metric described by (36) corresponding to  and
and .
.
Figure 4. Diagram showing that the particle horizon of the space-time metric described by (36) is made up of curved segments corresponding to various  values.
values.
space-time is expanding at such a rate that the photon never gets to the observer. As Eddington has put it, “light is then like a runner on an expanding track, with the win- ning post (observer) reseeding from him forever” [18].
In such cases there will be two classes of photons on every null geodesic through the observer: those which reach the observer at a finite time and those who do not. They are separated by the aggregate of photons (light front) that reach exactly at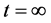 . The light front is called observer’s event horizon. The existence and mo- tion of an event horizon depend on the form of expansion parameter. The event horizons in cosmology have been studied by [15].
. The light front is called observer’s event horizon. The existence and mo- tion of an event horizon depend on the form of expansion parameter. The event horizons in cosmology have been studied by [15].
Figure 5. Diagram showing the direct comparison between Event and Particle horizons of the space-time metric (36) as described in the Section 6. Here we have selected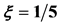 .
.
2) Particle horizon
Suppose that very first photons (light front) emitted by the observer at a “big-bang” event are still around. As this light front sweeps outwards, towards more and more galaxies, the observer at the big-bang and these galaxies see each other for the very first time (cosmic instant). Hence, at any cosmic instant this light front, called the observer’s particle horizon, divides all galaxies into two classes relative to the observer: those already in observer’s view and all others.
3) Some properties of horizons
a) Every galaxy, within A’s event horizon, except A, eventually possess out of it. For if B is such a galaxy, then A’s horizon photon in the direction of AB is within B’s event horizon, and will therefore reach B at a finite cosmic time. That is, when B passes out of A’s event horizon.
b) Every galaxy B within A’s event horizon remains visible forever at A. For, the event horizon itself brings a last view of B. As B approaches A’s event horizon in models with infinite expansion, its history, as seen at A, gets infinitely dilated, and its light infinitely red-shifted. In collapsing models B’s light gets infinitely blue-shifted as B approaches the event horizon.
c) As galaxies are overtaken by A’s particle horizon, they come into view at A with infinite red-shift in big- bang models, and infinite bleu-shift in models with unlim- ited past expansion.
d) If a model possesses no event horizon, every event at every galaxy is seen on every galaxy. For, an invisible event implies the existence of event horizon.
e) If a model possesses no particle horizon, every observer - if necessary by traveling from his original galaxy - can be present at any event at any galaxy. For, in principle, his only travel restriction is his forward light cone at creation; but that would be a particle horizon if all galaxies ware not always within it.
f) If an event horizon exists, two arbitrary events are in general not both knowable to one observer, even if he travels. For, consider two diametrically opposite events outside an event horizon. Their forward light cones can’t intersect. But to now either event means being in its forward light cone.
g) The event and particle horizons, if exist, must cross each other within the life time of the model. For, the par- ticle horizon was and the event horizon will be, at the fundamental particles associated with them.
h) When a model, in which both event and particle ho- rizons exist, is run backward in time (i.e. time reversed), the event horizon becomes the particle horizon and vice- versa.
3. Spherically Symmetric Space-Time Metric
The most general spherically space-time line element can be considered as
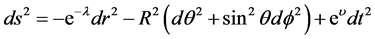 (1)
(1)
where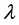 ,
, 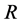 and
and 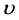 are functions of
are functions of  and
and 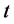 only. We assume that the material source of the gravitational field, filled in the metric, is an anisotropic fluid with the energy momentum tensor
only. We assume that the material source of the gravitational field, filled in the metric, is an anisotropic fluid with the energy momentum tensor
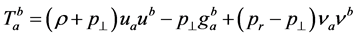 (2)
(2)
where
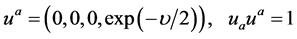 (3)
(3)
 (4)
(4)
and 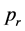 and
and 



After using (1) to (3) we get the following:










Using the directional derivatives 





We now directly write down the equations which govern the evolution of the system as below [19]:







where n denotes the baryon number density and we have written
We may mention here that the energy density of the free gravitational field which is coupled always to the material energy density as well as the cosmological con- stant plays a significant role in describing truly relativis- tic situations. We have taken, for simplicity, the coupling constant as unity. However, in order to raise the contri- bution of 

4. Kinematics of Spherically Symmetric Models
Spherically symmetric solutions can be classified according to their kinematical properties. The assumption of spherical symmetry implies that rotation 










In view of these expression, the anisotropy in the 4-dimensional space-time, denoted by

takes the form

and similarly the Raychaudhuri equation [20]

using (3) can be rewritten as

The quantity 

where the upper and lower signs respectively correspond to expanding and contracting models. It has been sug- gested that a physically meaningful cosmological model should evolve in such a way that 
5. Formula for Horizons
With the coordinates 





In the space-time model, described by [21]

The equation of motion (28) takes the form

In (29), a particle horizon exists, since the condition for which
is satisfied. Thus, the equation of the horizon is given by

and thus the particle 





We have given the diagrammatic representation of this particle horizon in Figure 1.
We now consider the space-time model described by [21]

where 


where 




We now consider the space-time model described by [21]

in which a particle horizon exists and its equation is given by

where 




We now consider a more general metric described by [21]

With the constant 


If the observer 









It appears, from (38), that the evaluation period of the particle horizon is divided into three parts respectively: initial, intermediate and final epochs. As 
1) In the initial epochs, the particle horizons with increasing values of 
2) In the intermediate epochs, the farther horizons are over taken by their preceding ones’ in a systematic man- ner. That is, in the process the nearest horizon over takes all others and becomes the farthest to the observer, while the farthest horizon allows all others to take over it and becomes the nearest and so on.
3) In the final epochs, with the reversed length scales, i.e. larger the distance of horizon from the observer higher the corresponding value of
We have given diagrammatic representation of the particle horizon described by (38) for 

4) Small segments of the horizons of 

We have given a diagram in Figure 4 which demonstrates the property 5).
6. Comparison between the Event and Particle Horizons
In the space-time metric described by (36), both Event and Particle horizons exist. The Event horizon [15] is
described by the equation

graphical representation is shown in Figure 3. Here


parison between the Event and Particle horizon.
Event horizon is a spherical light front converging towards the observer while Particle horizon is that diverging away from the observer, as time progresses. However, Event and Particle horizons are inversely propagating (oppositely travelling) light fronts (spherical) to and from an observer. Graphical comparison, illustrating this fact, is shown in Figure 5.
7. Conclusion
We have derived the equations of particle horizons for some cosmological solutions. Also, we have demonstrated them graphically. It is well known that in F-R-W models ε vanishes but horizons exist and thus the former has no bearing on the latter. However, we have shown in Figure 4 that ε, equivalently ξ, is related with horizons. As ε grows, the corresponding particle horizon increases and thus the radius of the visible universe increases.
8. Acknowledgements
My profound thanks are due to the referee for his valuable and constructive comments and to my colleague Dr. Ayele Taye Goshu for his stimulating discussions.
References
- 1. R. C. Tolman, Proceedings of the National Academy of Sciences of USA, Vol. 20, 1934, p. 69.
- 2. G. C. Omer, The Astrophysical Journal, Vol. 109, 1949, p. 164.
- 3. H. Bondi, Monthly Notices of the Royal Astronomical Society, Vol. 107, 1947, p. 410.
- 4. J. Krishna Rao, Current Science, Vol. 35, 1966, p. 389.
- 5. J. Krishna Rao, General Relativity and Gravitation, Vol. 2, 1971, pp. 385-386. http://dx.doi.org/10.1007/BF00758157
- 6. J. Krishna Rao, Journal of Physics (London), Vol. A5, 1972, p. 479.
- 7. J. Krishna Rao, General Relativity and Gravitation, Vol. 2, 1973, p. 351. doi:10.1007/BF00771004
- 8. J. Krishna Rao, Pramana: Journal of Physics, Vol. 34, 1990, p. 423.
- 9. J. Krishna Rao, Journal of the Institute of Mathematics, Vol. 51, 1995, p. 57.
- 10. K. Purnachandra Rao, Unpublished Ph.D. Thesis, Bhavnagar University, Bhavnagar, 1997.
- 11. K. Purnachandra Rao, et al., Mathematics Today, Vol. 16, 1998, p. 25.
- 12. K. Purnachandra Rao, Mathematics Today, Vol. 17, 1999, p. 29.
- 13. K. Purnachandra Rao, Mathematics Today, Vol. 21, 2005, p. 31.
- 14. K. Purnachandra Rao, Mathematics Today, Vol. 24, 2008, p. 17.
- 15. K. Purnachandra Rao, Mathematics Today, Vol. 25, 2009, p. 34.
- 16. K. Purnachandra Rao, Mathematics Today, Vol. 27, 2011, p. 54.
- 17. M. A. H. MacCallum, In: V. D. Sabbata, Ed., The Origin and Evolution of Galaxies, World Scientific Pub. Co., 1982.
- 18. M. A. H. MacCallum, In: B. R. Iyer, A. Kembhavi, J. V. Narliker and C. V. Vishveshwara, Eds., Highlights in Gravitation and Cosmology, University Press, Cambridge, 1988.
- 19. A. K. Raychaudhuri, Physical Review, Vol. 98, 1955, pp. 1123-1126. doi:10.1103/PhysRev.98.1123
- 20. W. Rindler, Monthly Notices of the Royal Astronomical Society, Vol. 116, 1956, p. 662.
- 21. W. Rindler, “Essential Relativity: Special, General and Cosmological,” Springer-Verlag, 1977.







