Journal of Modern Physics
Vol.4 No.6(2013), Article ID:32991,5 pages DOI:10.4236/jmp.2013.46104
Coupling Effects of Depletion Interactions in Three-Sphere Systems with Different Size Ratio of Largeto Small-Sphere
1Department of Physics and Electronic Engineering, Zhangzhou Normal University, Zhangzhou, China
2Department of Physics, Hunan Normal University, Changsha, China
Email: cmxiao@hunnu.edu.cn
Copyright © 2013 Zhouan Zhou et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 28, 2013; revised April 30, 2013; accepted May 25, 2013
Keywords: Coupling Effects of Depletion Interactions; Three-Sphere Systems; Size Ratio
ABSTRACT
The coupling effects of depletion interactions in three-sphere systems with different size ratio of largeto small-sphere are studied by Monte Carlo simulations in this paper. The numerical results show that this coupling effect is affected by the size ratio of largeto small-sphere: the larger the size ratio is, the larger the coupling effect will be.
1. Introduction
Recently, coupling effects of depletion interaction were reported in the three-sphere system or in the two-sphere system confined by two plates [1-3]. It was pointed out that when a large-sphere is suffered by more than one depletion force, these depletion forces will couple with each other and results in a strengthened depletion force. As a new finding, the coupling effect is a very interesting and significant topic for us to study, since the dynamic behavior of particles and the structure of the colloidal system will be affected by the strengthened depletion interactions. With the aid of the concept of excluded volume, Asakura and Oosawa (AO) suggested that, the mechanism about the depletion force is just related to geometrical factor, therefore it is very simple [4]. However, the coupling effect reminds us that it is not as simple as what they told. Obviously, further investigations on the coupling effects of the depletion forces are needed. For simplicity, in previous studies, the size ratio of largeto small-sphere of these systems is almost unchanged [5- 14]. On the other hand, the coupling effect will be affected by the parameter of size ratio, from which the nucleation of cluster is also affected: the nucleation packing of cluster will be easier to go on if it increases with the increase of size ratio of largeto small-sphere. In this paper, through the three-sphere system schematically illustrated by Figure 1(a), the relation between the coupling effect and size ratio of largeto small-sphere will be taken into consideration. In this system, the large sphere B is placed between the two spheres A and C. Apparently it is suffered two opposite depletion forces from A and C at the same time. However, it was found that, in this three-sphere system, the depletion forces acted on B are larger than that of the two-sphere system described by Figure 1(b), where the sphere C is taken out of from the three-sphere system. To describe this coupling effect of depletion interactions clearly, a parameter should be introduced. According to the definition of three-body interaction, the difference of the depletion forces in the three systems demonstrated by Figures 1 (a)-(c) can be used to describe the coupling effect.
In this paper, the model and theory are presented in Section 2, and the numerical results and a simple discussion will be given in Section 3, finally a summary of our study will be given in Section 4.
2. Theory and Model
It is well known that the hard spheres mixture is characterized by the pair potential of
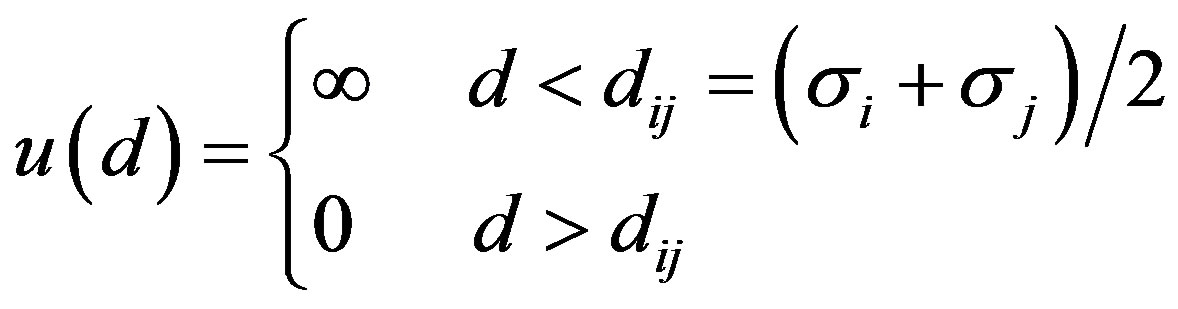 (1)
(1)
where d is the distance between the two spheres in diameters  and
and , respectively. The force exerted on the big sphere of radius R by a small sphere of radius r
, respectively. The force exerted on the big sphere of radius R by a small sphere of radius r
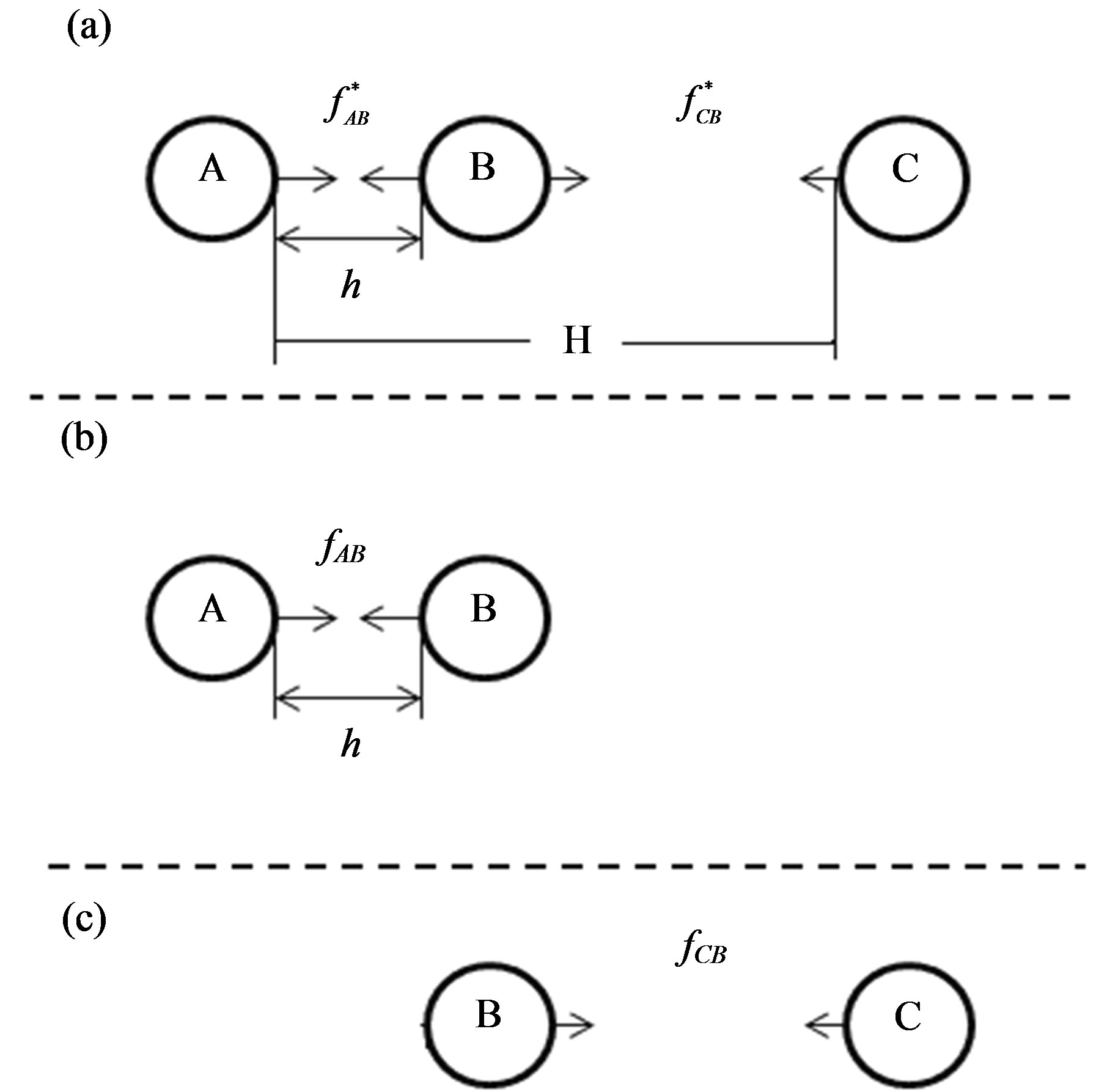
Figure 1. (a) Schematic diagram of the three-sphere system consisting of A, B and C; (b) is the two-sphere system where C is taken out of from (a); (c) is another two-sphere system where A is taken out of from (a). The dashed lines between (a) and (b), (b) and (c), are just used to separate the three systems. h is the separation of spheres A and B, and H the separation of A and C.
can then be written as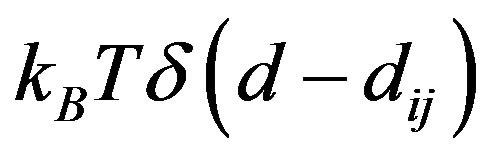 . Consequently, the depletion force is the total force acted on the large sphere from the small spheres, and can be usually determined through the acceptance ratio method (ARM): if the potential and partition function of two systems are
. Consequently, the depletion force is the total force acted on the large sphere from the small spheres, and can be usually determined through the acceptance ratio method (ARM): if the potential and partition function of two systems are  and
and  respectively, where
respectively, where 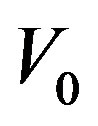 and
and 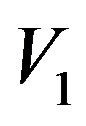 are the external potentials corresponding to the two large spheres located at different positions, the free energy difference between these two systems is given by the following expression [6,11,15],
are the external potentials corresponding to the two large spheres located at different positions, the free energy difference between these two systems is given by the following expression [6,11,15],
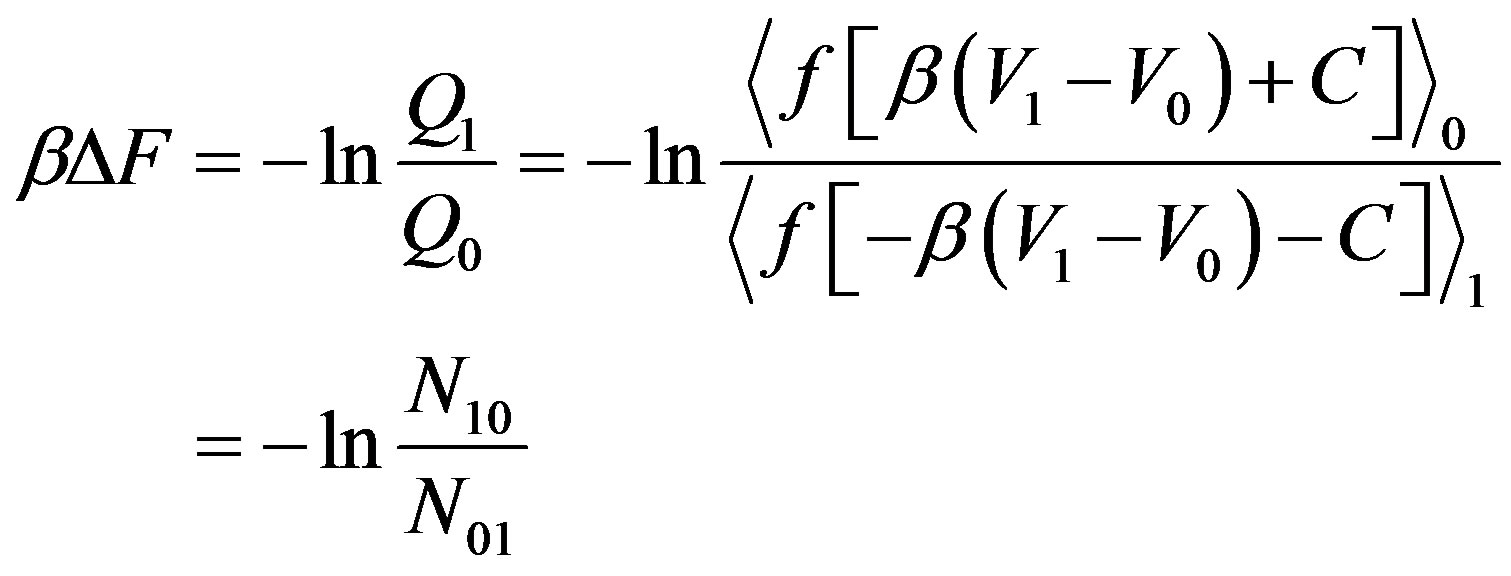 (2)
(2)
where 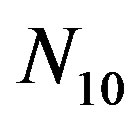 is the number of samples drawn out from
is the number of samples drawn out from  simulated samples, which generated with the potential
simulated samples, which generated with the potential  where
where  is not infinite;
is not infinite; 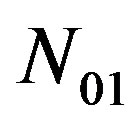 is the number of samples drawn out from
is the number of samples drawn out from 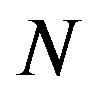 simulated samples, which generated with potential
simulated samples, which generated with potential 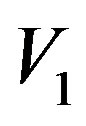 where
where 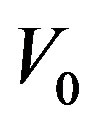 is not infiniteand
is not infiniteand  is the Fermi function, and C is a constant which is usually set to a value of 0 for a hard sphere system.
is the Fermi function, and C is a constant which is usually set to a value of 0 for a hard sphere system.
We note that the depletion force can be determined by the differential of the free energy of the system obtained through Equation (2). Besides, it is important to emphasize that if there are many depletion forces acted on a sphere at the same time, only the resultant force corresponding to the free energy will be determined by ARM.
For the three-sphere system, a parameter is introduced to describe the coupling effect:
 . (3)
. (3)
where f is the resultant force of the three-sphere system described by Figure 1(a), 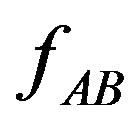 ,
, 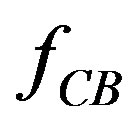 are the two forces acted on large sphere B of the two-sphere systems described by Figures 1(b) and (c) respectively. In fact, in the three-sphere system, due to the presence of large spheres A and C, the two component forces acted on large sphere B are
are the two forces acted on large sphere B of the two-sphere systems described by Figures 1(b) and (c) respectively. In fact, in the three-sphere system, due to the presence of large spheres A and C, the two component forces acted on large sphere B are ,
,  , and the relation between them is,
, and the relation between them is,
 . (4)
. (4)
Obviously, if there is no coupling effect between  and
and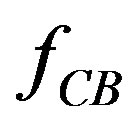 ,
, 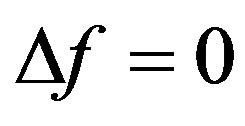 , otherwise
, otherwise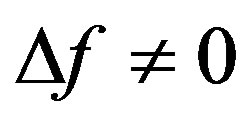 , so
, so 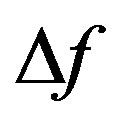 can be used to describe the coupling effect. For the sake of simplicity, we suppose that, in all the systems mentioned above, the positions of spheres A and C are fixed, only B moves from the position of the contact of A to the middle point of A and C, then the depletion forces f,
can be used to describe the coupling effect. For the sake of simplicity, we suppose that, in all the systems mentioned above, the positions of spheres A and C are fixed, only B moves from the position of the contact of A to the middle point of A and C, then the depletion forces f,  ,
, 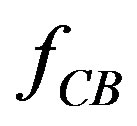 are determined by ARM through the systems described by Figures 1(a)-(c) respectively. The parameter h is the separation of A and B, and H is the separation of A and C.
are determined by ARM through the systems described by Figures 1(a)-(c) respectively. The parameter h is the separation of A and B, and H is the separation of A and C.
3. Results and Discussions
In this section, only the unconfined three-sphere systems and the corresponding two two-sphere systems with size ratio of largeto small-sphere R/r = 3, 5, will be studied, respectively. In the simulations, the two or three large hard spheres are placed along 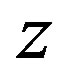 direction of the cell box of size
direction of the cell box of size , but the small spheres are randomly distributed around the macro spheres to form a fluid; the number of micro-ions
, but the small spheres are randomly distributed around the macro spheres to form a fluid; the number of micro-ions  is determined by the given volume fraction
is determined by the given volume fraction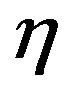 , defined as
, defined as 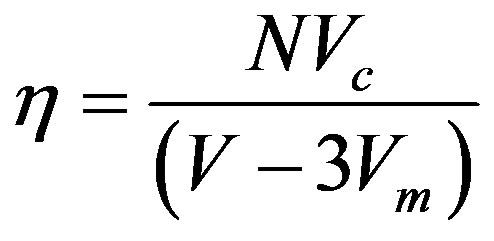 or
or  for the threeor two-sphere system respectively, where
for the threeor two-sphere system respectively, where 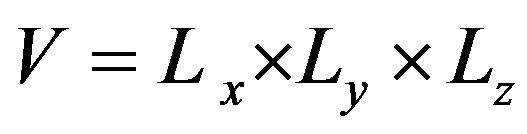 is the total volume of the cell box,
is the total volume of the cell box, 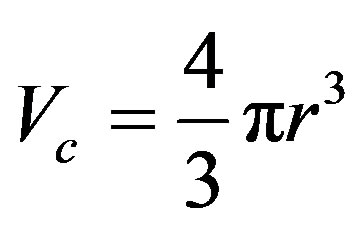 is for the volume of the microsphere,
is for the volume of the microsphere,  denotes the volume of the macrosphere. As unconfined systems, the period boundary condition is applied to all the three directions of X, Y and Z in the Monte Carlo simulations. Then the configurations of the micro-spheres will be sampled according to the Metropolis algorithm [15] with the two macrospheres A and C fixed while B is moved from the contact of A to the middle point of A and C. Each micro-sphere is orderly chosen involving a trial displacement. Except for an overlapping with the macro-spheres and the other micro-spheres, the new position of the micro sphere is randomly accepted. In our simulations,
denotes the volume of the macrosphere. As unconfined systems, the period boundary condition is applied to all the three directions of X, Y and Z in the Monte Carlo simulations. Then the configurations of the micro-spheres will be sampled according to the Metropolis algorithm [15] with the two macrospheres A and C fixed while B is moved from the contact of A to the middle point of A and C. Each micro-sphere is orderly chosen involving a trial displacement. Except for an overlapping with the macro-spheres and the other micro-spheres, the new position of the micro sphere is randomly accepted. In our simulations, 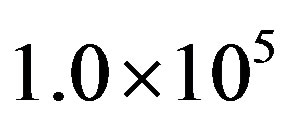 Monte Carlo steps (MCS) are used for the equilibrium of the system and other
Monte Carlo steps (MCS) are used for the equilibrium of the system and other  MCS to collect data, and the depletion potential is set as 0 while the two macrospheres A and B are at contact, i.e., h = 0. In this way, the depletion potentials, then the corresponding depletion forces in the unconfined, twoand three-sphere systems,
MCS to collect data, and the depletion potential is set as 0 while the two macrospheres A and B are at contact, i.e., h = 0. In this way, the depletion potentials, then the corresponding depletion forces in the unconfined, twoand three-sphere systems,  ,
,  , and
, and , are determined by ARM respectively. For the sake of simplicity, the cases corresponding the unconfined three-sphere systems with R/r = 3, 5, and volume fraction
, are determined by ARM respectively. For the sake of simplicity, the cases corresponding the unconfined three-sphere systems with R/r = 3, 5, and volume fraction 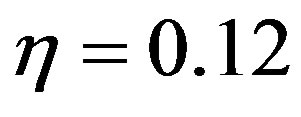 and 0.23, were studied, respectively, and the corresponding depletion forces are shown in Figures 2-5, respectively. In these figures, the depletion force
and 0.23, were studied, respectively, and the corresponding depletion forces are shown in Figures 2-5, respectively. In these figures, the depletion force 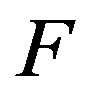 is plotted as a function of
is plotted as a function of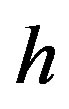 , and the units of F and h are
, and the units of F and h are 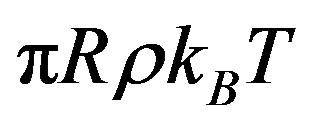 and
and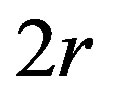 , respectively, where
, respectively, where  is the number density of the small sphere,
is the number density of the small sphere, 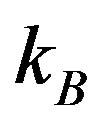 the Boltzmann constant, T the absolute temperature. In Figures 2-5, the short-dashed lines denote the depletion forces of the three-sphere system, the solid and longdashed lines denote the two-sphere systems described by Figures 1(b) and (c), respectively. From Figures 2-5, it’s evident that, 1) no matter the volume fraction is large or small, the depletion force between spheres B and C is almost 0; 2) the depletion force of the three-sphere system is larger than that of the other two-sphere system (consisting of A and B). Furthermore, according to Equation (4), the corresponding depletion force difference of the three-sphere system and the two corresponding two-sphere systems
the Boltzmann constant, T the absolute temperature. In Figures 2-5, the short-dashed lines denote the depletion forces of the three-sphere system, the solid and longdashed lines denote the two-sphere systems described by Figures 1(b) and (c), respectively. From Figures 2-5, it’s evident that, 1) no matter the volume fraction is large or small, the depletion force between spheres B and C is almost 0; 2) the depletion force of the three-sphere system is larger than that of the other two-sphere system (consisting of A and B). Furthermore, according to Equation (4), the corresponding depletion force difference of the three-sphere system and the two corresponding two-sphere systems 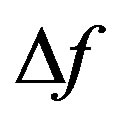 are also determined and theresults for
are also determined and theresults for 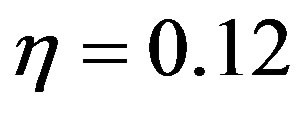 and 0.23 are shown in Figures 6 and 7, in which the dashed and solid lines are for the confined and unconfined systems respectively. From Figures 6 and 7, it is evident that
and 0.23 are shown in Figures 6 and 7, in which the dashed and solid lines are for the confined and unconfined systems respectively. From Figures 6 and 7, it is evident that , so the deple
, so the deple

Figure 2. The depletion forces of the unconfined threesphere system (described by the dotted lines) and of the corresponding two-sphere systems (by the solid and dotdashed lines respectively). The volume fraction is  and the size ratio is R/r = 3.
and the size ratio is R/r = 3.
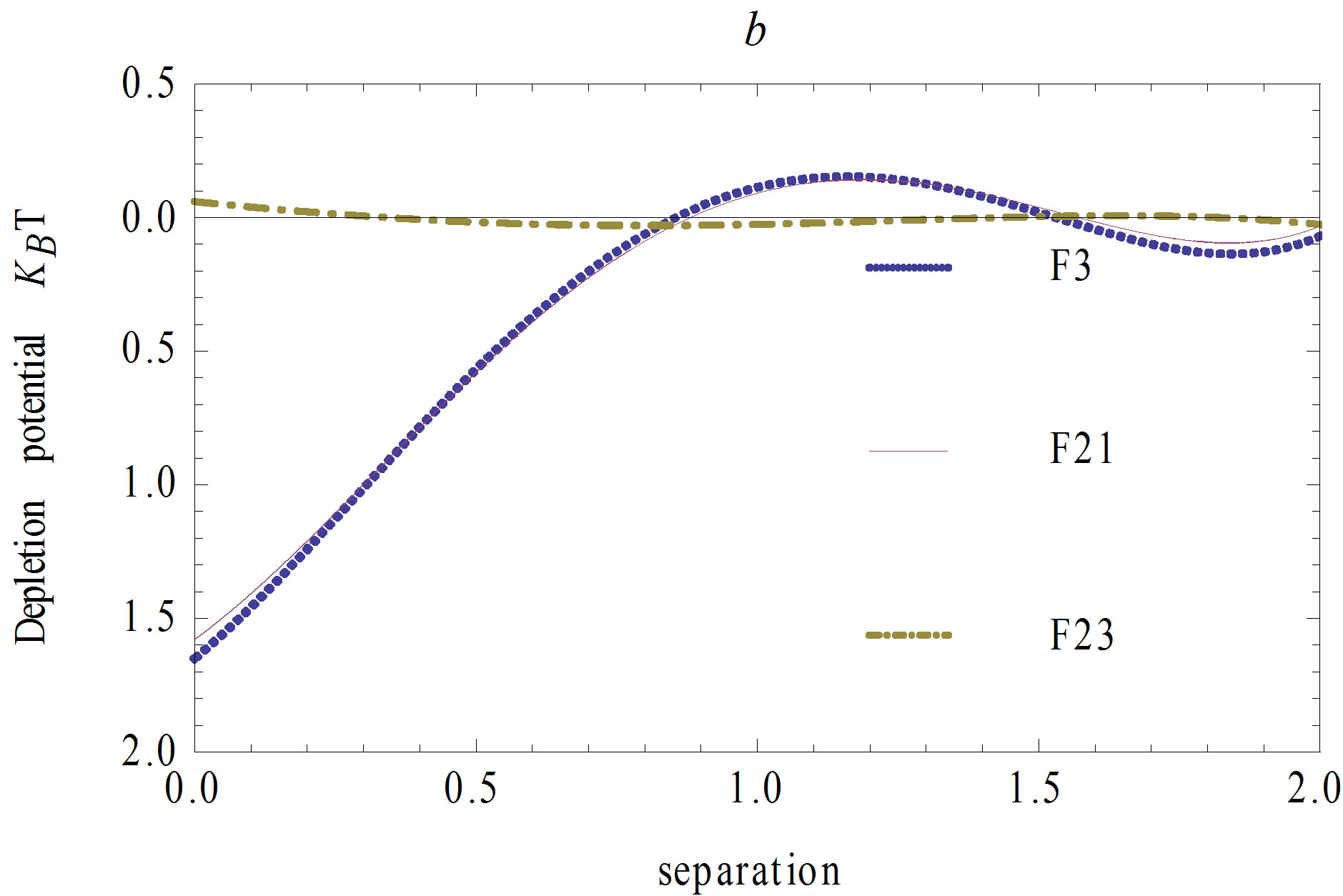
Figure 3. The depletion forces of the unconfined threesphere system (described by the dotted lines) and of the corresponding two-sphere systems (by the solid and dotdashed lines respectively). The volume fraction is 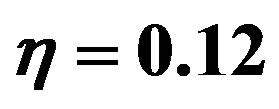 and the size ratio is R/r = 5.
and the size ratio is R/r = 5.
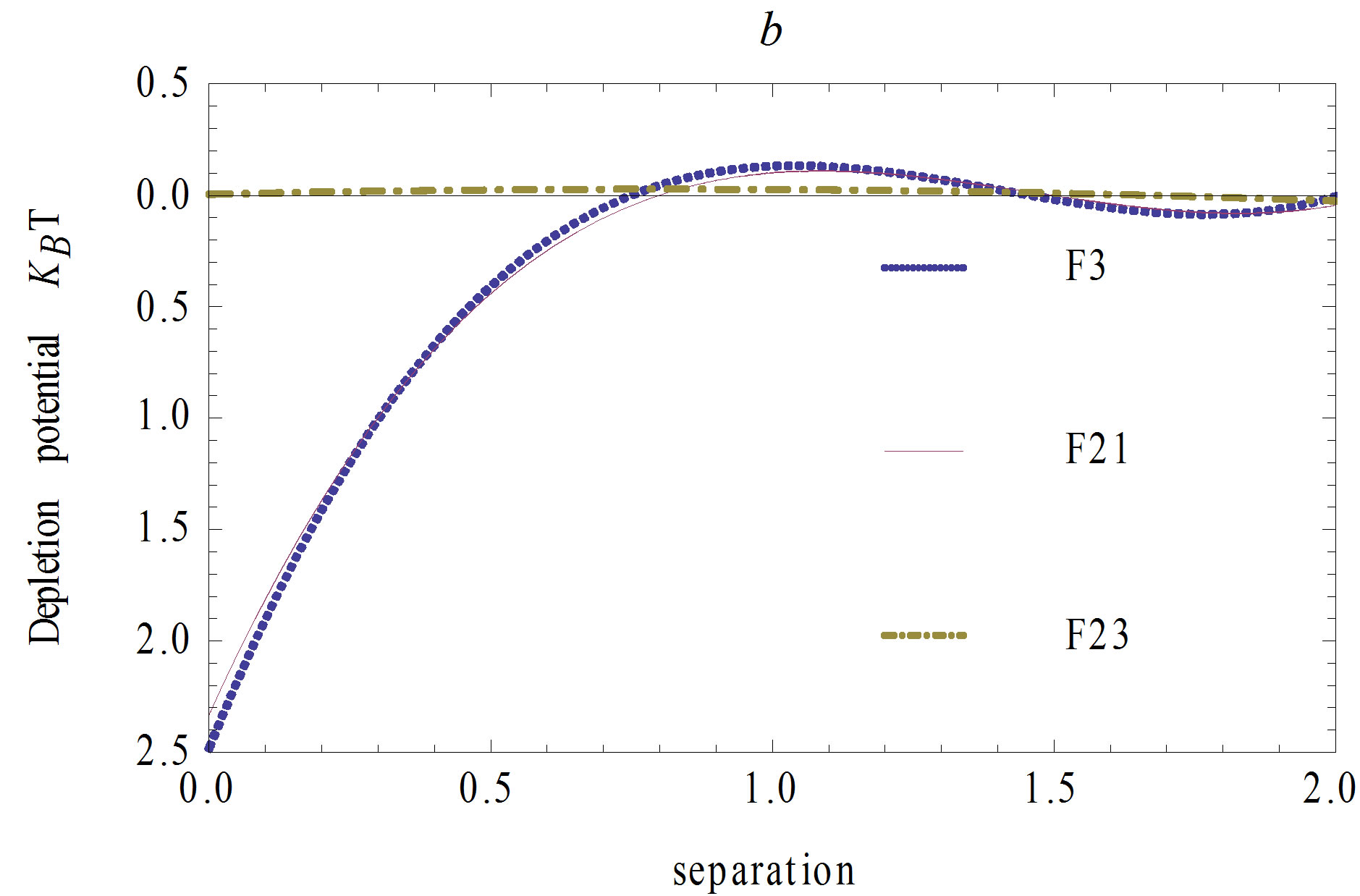
Figure 4. The depletion forces of the unconfined threesphere system (described by the dotted lines) and of the corresponding two-sphere systems (by the solid and dotdashed lines respectively). The volume fraction is 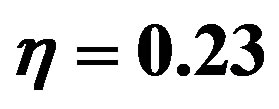 and the size ratio is R/r = 3.
and the size ratio is R/r = 3.

Figure 5. The depletion forces of the unconfined threesphere system (described by the dotted lines) and of the corresponding two-sphere systems (by the solid and dotdashed lines respectively). The volume fraction is  and the size ratio is R/r = 5.
and the size ratio is R/r = 5.
tion interactions acted on the sphere B are coupled with each other. In addition, from Figures 6 and 7 we also find that, 1) 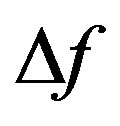 is enlarged when the volume fraction of the system increases from 0.12 to 0.23; 2)
is enlarged when the volume fraction of the system increases from 0.12 to 0.23; 2)  is also enlarged when the size ratio of largeto smallsphere of the system of R/r is increased from 3 to 5. In other words, the larger the volume fraction is, the larger the coupling effect of the depletion interactions will be; the larger the size ratio is, the larger the coupling effect of the depletion interactions will be. This is very important for us to get the physical viewpoint of nucleation. Supposing in a binary colloidal system, free large-spheres are continually pushed together by small-spheres, a cluster consisting of the packed spheres is therefore built up. Furthermore, with the increasing size of the cluster, it will suffer more and more strengthened depletion interactions from the small-spheres, because both the depletion interactionsand the coupling effect of these depletion interactions will increase with the increase of the size ratio of the largeor small sphere to cluster. As a result, the cluster will grow larger and larger, even a nucleation will turn
is also enlarged when the size ratio of largeto smallsphere of the system of R/r is increased from 3 to 5. In other words, the larger the volume fraction is, the larger the coupling effect of the depletion interactions will be; the larger the size ratio is, the larger the coupling effect of the depletion interactions will be. This is very important for us to get the physical viewpoint of nucleation. Supposing in a binary colloidal system, free large-spheres are continually pushed together by small-spheres, a cluster consisting of the packed spheres is therefore built up. Furthermore, with the increasing size of the cluster, it will suffer more and more strengthened depletion interactions from the small-spheres, because both the depletion interactionsand the coupling effect of these depletion interactions will increase with the increase of the size ratio of the largeor small sphere to cluster. As a result, the cluster will grow larger and larger, even a nucleation will turn

Figure 6. The difference of depletion forces of the threesphere systems. The volume fraction is  and the size ratio is R/r = 5, 3 respectively.
and the size ratio is R/r = 5, 3 respectively.
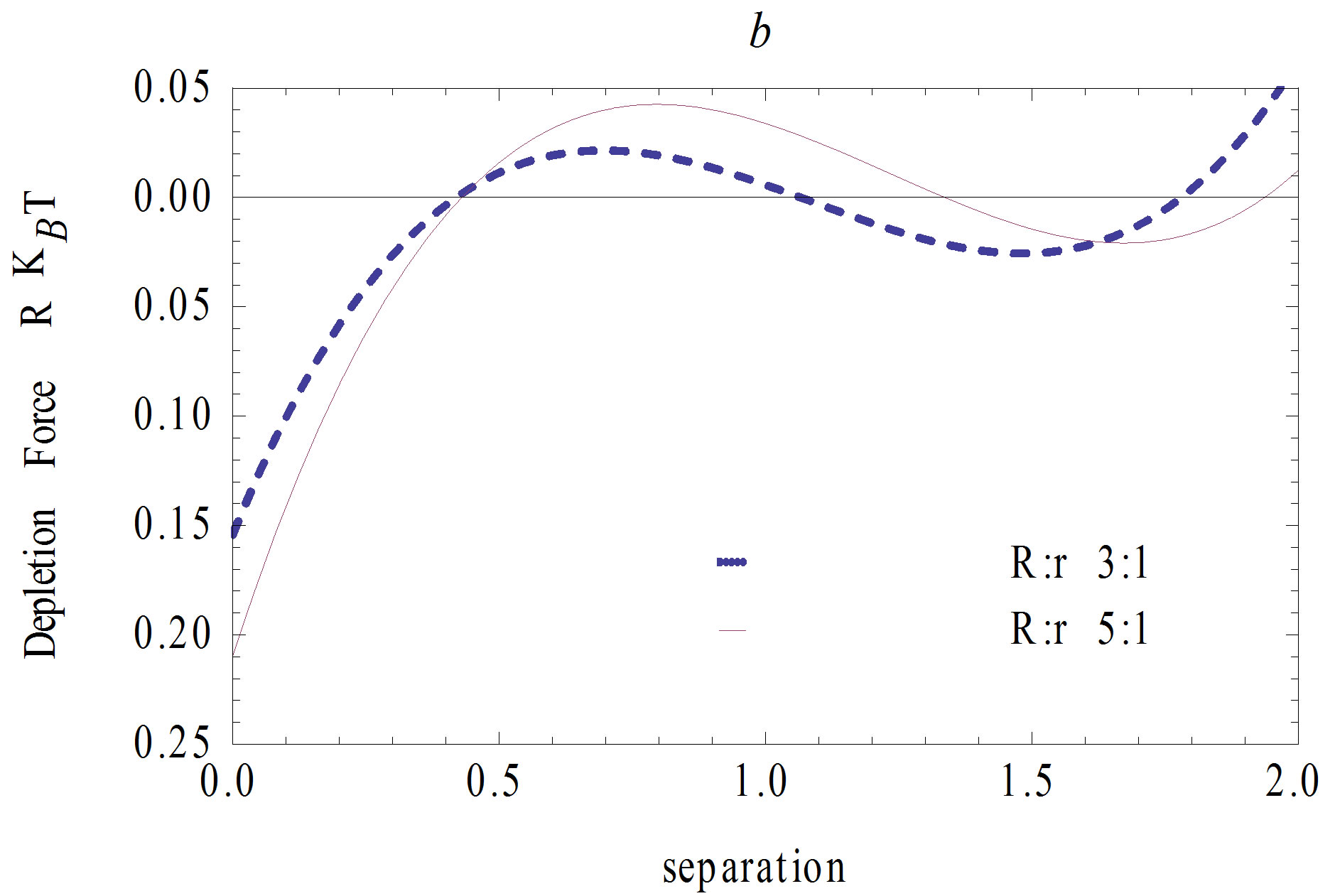
Figure 7. The difference of depletion forces of the threesphere systems. The volume fraction is 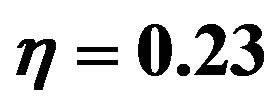 and the size ratio is R/r = 5, 3 respectively.
and the size ratio is R/r = 5, 3 respectively.
out. In other words, the coupling effect of depletion interactions is helpful for the nucleation packing.
4. Conclusion
In conclusion, we have studied the depletion interactions in the unconfined three-sphere systems with different size ration through Monte Carlo simulations. It is found that this coupling effect is clearly and completely described by the parameter of the depletion force difference of the three-sphere system and the two corresponding twosphere systems. It is also found that the coupling effect of depletion force is affected by both the size ratio and the volume fraction of the system.
5. Acknowledgements
Project supported by the Scientific Research Fund of Hunan Provincial Education Department, China (Grant No. 10A075).
REFERENCES
- H. X. Gao, Z. S. Chen, C. S. Li and C. M. Xiao, Journal of Modern Physics, Vol. 3, 2012, pp. 918-922. doi:10.4236/jmp.2012.39119
- L. X. Wang, H. X. Gao and C. M. Xiao, Acta Physica, Vol. 58, 2009, p. 5865.
- C. M. Xiao, J. Y. Guo and P. Hu, Physical Review E, Vol. 73, 2006, Article ID: 061403. doi:10.1103/PhysRevE.73.061403
- S. Asakura and F. J. Oosawa, Journal of Chemical Physics, Vol. 22, 1954, p. 1255.
- B. Götzelmann, R. Evans and S. Dietrich, Physical Review E, Vol. 57, 1998, pp. 6785-6800. doi:10.1103/PhysRevE.57.6785
- C. M. Xiao and J. Y. Guo, Europhysics Letters, Vol. 73, 2006, p. 443. doi:10.1209/epl/i2005-10397-2
- J. Z. Wu, D. Bratko, H. W. Blanch and J. M. Paausnitz, Journal of Chemical Physics, Vol. 113, 2000, p. 3360. doi:10.1063/1.1287173
- D. Goulding and S. Melchionna, Physical Review E, Vol. 64, 2001, Article ID: 011403. doi:10.1103/PhysRevE.64.011403
- J. M. Brader, M. Dijkstra and R. Evans, Physical Review E, Vol. 63, 2001, Article ID: 041405. doi:10.1103/PhysRevE.63.041405
- D. M. Zhu, W. H. Li and H. R. Ma, Journal of Physics: Condensed Matter, Vol. 15, 2003, p. 8281. doi:10.1088/0953-8984/15/49/007
- W. H. Li and H. R. Ma, Physical Review E, Vol. 66, 2002, Article ID: 061407. doi:10.1103/PhysRevE.66.061407
- D. A. Triplett and K. A. Fichthorn, Journal of Chemical Physics, Vol. 133, 2010, Article ID: 144910. doi:10.1063/1.3503975
- H. X. Gao and C. M. Xiao, Physics Letters A, Vol. 362, 2007, pp. 234-238. doi:10.1016/j.physleta.2006.10.019
- C. M. Xiao, J. Y. Guo and P. Hu, Chinese Physics Letters, Vol. 23, 2006, p. 1482. doi:10.1088/0256-307X/23/6/035
- C. H. Bennett, Journal of Computational Physics, Vol. 22, 1976, pp. 245-268. doi:10.1016/0021-9991(76)90078-4

