Journal of Modern Physics
Vol.5 No.12(2014), Article ID:48111,8 pages
DOI:10.4236/jmp.2014.512113
Semimicroscopic Dispersive Analysis of Nuclear-Nuclear Collisions on the Basis of Folding Potential
Abdolmajid Izadpanah1, Marzieh Yousefi2
1Department of Physics, Golestan University, Gorgan, Iran
2Department of Physics, School of Fariman Payame Nor, Fariman, Iran
Email: amjizad@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 16 February 2014; revised 12 March 2014; accepted 7 April 2014
ABSTRACT
A semimicroscopic analysis of a set of experimental data of elastic α + 12C scattering was performed at several laboratory energies. The Woods-Saxon parameters were adjusted to obtain the best χ2 fit to the scattering data. The energy systematics of the positions of Airy minima was constructed, and it was shown that their positions depend linearly on the inverse center of mass energy. The parameters of the model potential have been determined unambiguously. It has been shown that the energy dependence of the volume integrals satisfies the dispersion relation and agrees well with the results obtained within a phenomenological analysis. Also, it has been shown that the found positions of the Airy minima satisfy the rule of the quadratical dependence of the position of the Airy minima on the reduced mass of the colliding nuclei.
Keywords:Nuclear Dispersion Anomaly, Optical Model Potential, Nuclear Rainbow, Airy Minima

1. Introduction
The essence of the potential approach, that has been applied to describe elastic scattering and direct reaction in nucleus-nucleus collisions at energies in the range extending up to 100 MeV per nucleon, is that the system of two interacting nuclei at the given energy in the elastic channel can be described by a model-dependent wave function that is found by solving the single-particle Schrödinger equation with an effective potential [1] . Effective potential is nonlocal, complex-valued and energy-dependent and can be represented as the sum of two components: static component or “mean-field potential” that represents the interaction of nuclei in their ground states and is energy-independent and dynamical component or “dynamical polarization potential” (DPP) that carries information about all possible inelastic channels of the interaction between colliding nuclei.
The new and important point in this work is the calculation of the dispersion relation between the real and imaginary parts of the dynamical polarization potential. This relation is a result of the causality principle: a scattered wave cannot be emitted before the interaction has occurred [2] .
The model wave function may be written in terms of the complete set of internal wave functions of the projectile (a) and target (A) nuclei as [1]
 (1)
(1)
where
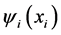 is the internal wave functions of colliding nuclei in their ground states. The problem
is reduced to the single-particle Schrödinger equation for scattering wave
function
is the internal wave functions of colliding nuclei in their ground states. The problem
is reduced to the single-particle Schrödinger equation for scattering wave
function
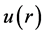 that describes the motion of the particle with reduced mass
that describes the motion of the particle with reduced mass
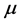 in effective complex potential:
in effective complex potential:
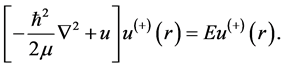 (2)
(2)
This equation is the basis of the optical model formulation that its essence is the construction of the effective potential model can be written
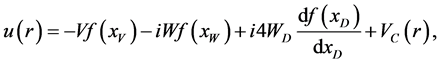 (3)
(3)
where ,
,
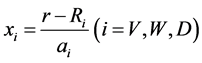 , is the Woods-Saxon form factor. Here
, is the Woods-Saxon form factor. Here
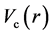 is Coulomb potential. Strength parameters
is Coulomb potential. Strength parameters
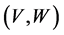 “depths of potential” and geometric parameters (radii and diffuseness) are obtaining
using the analysis of the elastic scattering experimental angular distributions.
The parameters are adjusted to obtain the best
“depths of potential” and geometric parameters (radii and diffuseness) are obtaining
using the analysis of the elastic scattering experimental angular distributions.
The parameters are adjusted to obtain the best
 fit to the scattering data.
fit to the scattering data.
One of the approaches to construction of effective potential is microscopic approach: attempt to understand interaction of two nuclei in terms of the motions of individual nucleons and their interactions. Static component, that is the matrix element of the real effective nucleon-nucleon interaction, is the ground states wave functions of colliding nuclei
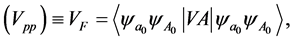 (4)
(4)
In this relation, already, dual nucleon-nucleon interaction,
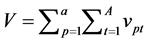 , is describing (t and p are used for target and projectile
nuclei, respectively) in generally this interaction is shown as
, is describing (t and p are used for target and projectile
nuclei, respectively) in generally this interaction is shown as
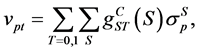 (5)
(5)
where
![]() is vector-radius according to nucleon p in the projectile a, and nucleon t in the
target A.
is vector-radius according to nucleon p in the projectile a, and nucleon t in the
target A.
The radial functions of the central component,
 , spin-orbital component,
, spin-orbital component,
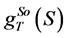 , tensor component,
, tensor component,
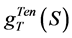 , and Coulomb component,
, and Coulomb component,
 (for protons) are the functions of the distance between
given pair nucleons. Here,
(for protons) are the functions of the distance between
given pair nucleons. Here,
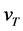 is the isoscalar
is the isoscalar
 and isovector
and isovector
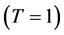 components of the effective nucleonnucleon interaction. The M3Y model of effective
nucleon-nucleon interactions in one of two versions, that which involves the input
Reid-Elliott potential [3] and that which involves
the input Paris potential [4] , is used to calculate
the mean-field potential.
components of the effective nucleonnucleon interaction. The M3Y model of effective
nucleon-nucleon interactions in one of two versions, that which involves the input
Reid-Elliott potential [3] and that which involves
the input Paris potential [4] , is used to calculate
the mean-field potential.
The radial part of the various components of interaction is shown by the sum of the Yukawa’s potentials. But this model of interaction is averaged over the energy and density and is not dependent on them explicitly. Obviously, it is very difficult to abandon the energy and density dependence. The density dependence is included in effective nucleon-nucleon interactions (central direct and exchange components in this case) in the form of a density-dependent factor multiplied by the M3Y model interaction (indices being suppressed):
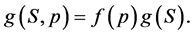 (6)
(6)
In the present study, we use the parametrization
 (7)
(7)
in the CDM3Y6 version, where the parameters involved were fitted to the properties of cold nuclear matter [5] , but in contrast to [5] , here is not introduced additional energy dependence. The single-nucleon knockout exchange (SNKE) between the two ions will be the dominant contribution, especially for light ions, even in the multichannel case. In the approximation of single-nucleon knockout exchange, the mean-field potential can be expressed in terms of folding integrals for the direct and exchange components. Omitting spin variables and spin components, it can written
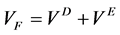 (8)
(8)
where
![]() is the direct component
is the direct component
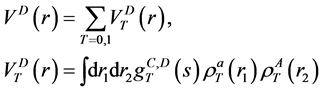 (9)
(9)
and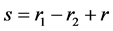 ,
,
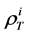 stands for the isoscalar
stands for the isoscalar
 or the isovector
or the isovector
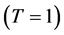 nuclear-density component
nuclear-density component
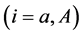 which are related in a standard way to the protonand neutron-density distributions
in each nucleus. The localized exchange component is given by
which are related in a standard way to the protonand neutron-density distributions
in each nucleus. The localized exchange component is given by
 (10)
(10)
Here
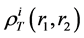 are the corresponding components of the nuclear density matrices. The local momentum
are the corresponding components of the nuclear density matrices. The local momentum
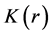 of relative motion is written as
of relative motion is written as
 (11)
(11)
where
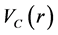 is the Coulomb potential.
is the Coulomb potential.
The density matrix, usually, is made with the aid of the modified Slater approximation (indices are suppressed)
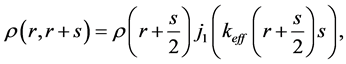 (12)
(12)
where
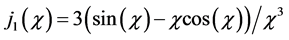 is the exchange correlation function. The effective-momentum components are determined
by an obtained expression from the generalized Thomas-Fermi approximation for the
kinetic-energy density
is the exchange correlation function. The effective-momentum components are determined
by an obtained expression from the generalized Thomas-Fermi approximation for the
kinetic-energy density
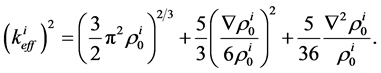 (13)
(13)
It was shown that, in the absence of the density dependence of nucleon-nucleon forces, the result of the calculation with the aid of (12) and (13) is virtually coincident with the result of the exact calculation. The use of the different version of the approximation in (13) leading to a modest distinction. Upon the inclusion of the density dependence, however, the deviation in both versions from the result of the “exact” calculation becomes sizable (smaller for the first, but greater for the second version) especially at low energies. All versions of the calculation of nuclear density matrices are rather cumbersome. In order to simplify the calculations, an approximate representation of the density matrix is used in the form [6]
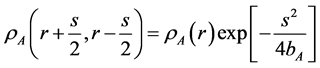 (14)
(14)
where an empirical nuclear density for
 is used and where
is used and where
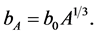 (15)
(15)
For
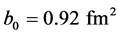 the approximation in (14) for the case of the alpha particle is coincident with
the density matrix calculated within the harmonic oscillator model. Therefore, this
representation was called a pseudooscillator approximation. Clearly, the microscopic
calculation of the dynamical component of the effective potential is difficult problem.
the approximation in (14) for the case of the alpha particle is coincident with
the density matrix calculated within the harmonic oscillator model. Therefore, this
representation was called a pseudooscillator approximation. Clearly, the microscopic
calculation of the dynamical component of the effective potential is difficult problem.
Other approach, that is widely used to construct effective potential, is called dispersion semimicroscopic approach. A semimicroscopic approach combines a microscopic calculation of the mean-field potential and a phenomenological construction of the dynamical polarization potential.
In this model, the dynamical polarization potential is constructed on the basis of physically justified combinations of the volume and surface forms whose geometric parameters are assumed to be independent of energy.
Furthermore, in this model the imaginary part of the central component DPP is represented
as the sum of the volume,
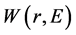 , and the surface,
, and the surface,
 , part and they are shown by the Woods-Saxon form and
its derivative. In this model, the optical model potential (Equation (2)) is represented
in the form
, part and they are shown by the Woods-Saxon form and
its derivative. In this model, the optical model potential (Equation (2)) is represented
in the form
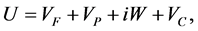 (16)
(16)
where the first term is the mean-field potential being calculated, the second term
is the real part of the phenomenological dynamical polarization potential (dispersive
correction), and the third term is its imaginary (absorptive) part. The absorption
includes the volume
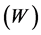 and surface
and surface
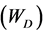 components. Here, they are represented by
components. Here, they are represented by
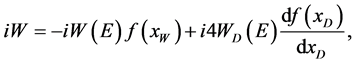 (17)
(17)
where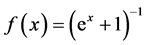 ,
,
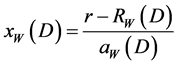 with
with
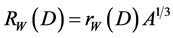 in the Woods-Saxon form factor, and the dispersive correction is given by the expression
in the Woods-Saxon form factor, and the dispersive correction is given by the expression
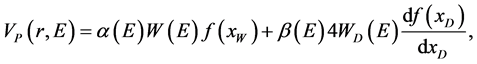 (18)
(18)
(![]() and
and
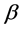 are free parameters) which follows from the dispersion relation if one assumes the
energy independence of geometric parameters (radius and diffuseness of the Woods-Saxon
form).
are free parameters) which follows from the dispersion relation if one assumes the
energy independence of geometric parameters (radius and diffuseness of the Woods-Saxon
form).
In this study, the Coulomb component
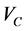 is simulated by the interaction potential of a pointlike charge with a uniformly
charged sphere of radius
is simulated by the interaction potential of a pointlike charge with a uniformly
charged sphere of radius
 that is given by [1]
that is given by [1]
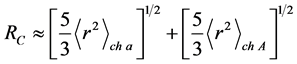 (19)
(19)
Keeping simplicity and convenience of application, such model effectively has smaller number of parameters and allows reducing ambiguity of the analysis.
The dispersive analysis of the volume integrals was performed here on the basis of the difference dispersion relation [7]
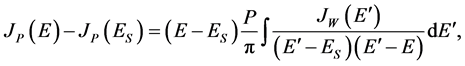 (20)
(20)
where the dependence
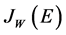 was approximated on the basis of the linear schematic model
[2] . Here, the volume integral of the real part of the potential is
the sum of two terms,
was approximated on the basis of the linear schematic model
[2] . Here, the volume integral of the real part of the potential is
the sum of two terms,
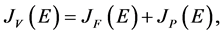 (21)
(21)
corresponding to the mean-field potential and the dispersion correction.
2. Semimicroscopic Dispersive Analysis of Elastic α + 12C Scattering
In order to analysis of experimental data, in this work, we used angular distributions
for elastic
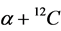 scattering that are available from the NNDC (EXFOR/CSISRS) database (http://www.nndc.bnl.gov/exfor).
An opticalmodel analysis was performed in fixing the geometric parameters
scattering that are available from the NNDC (EXFOR/CSISRS) database (http://www.nndc.bnl.gov/exfor).
An opticalmodel analysis was performed in fixing the geometric parameters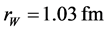 ,
,
 ,
,
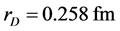 ,
,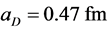 . These parameters were obtained in an individual
analysis involving a search for various combinations of geometric parameters, over
a reasonable interval of their values.
. These parameters were obtained in an individual
analysis involving a search for various combinations of geometric parameters, over
a reasonable interval of their values.
The values found for the remaining parameters and values of
![]() (
( is the number of experimental points in a given angular distribution)
are given in Table 1 for each data set in energy
under consideration. As a rule, the analysis was performed by using a constant experimental
error of 10 percent.
is the number of experimental points in a given angular distribution)
are given in Table 1 for each data set in energy
under consideration. As a rule, the analysis was performed by using a constant experimental
error of 10 percent.
Figure 1 shows the ratios of the experimental and
calculated differential cross sections for elastic
 scattering at various laboratories energies to the respective Rutherford cross sections.
Nuclear rainbow pattern clearly indicated in all energies and so it is possible
to construct energy systematics of the Airy minima positions.
scattering at various laboratories energies to the respective Rutherford cross sections.
Nuclear rainbow pattern clearly indicated in all energies and so it is possible
to construct energy systematics of the Airy minima positions.
In this work, three tests were used to avoid ambiguities in determining the potential: due to of rainbow structure, it is possible to construct energy systematics of the Airy minima positions. This systematics showed and confirmed the inverse-energy law and made it possible to select potential (see Figure 2). In Figure 2, the circles and triangles are indicated experimental Airy minima, while the stars are our calculated Airy minima. Lines 1 and 2 are corresponding to the positions of the first and second Airy minima, respectively. The results of the dispersive analysis using phenomenological approach (squares) and also semimicroscopic approach (circles) are displayed in Figure 3. This is second test. Both two approaches are shown some behaviors.
The curve introduced by Goncharov and Izadpanah [8] , for depending of Airy minima to reduced mass of col

Figure 1. Ratios of the differential cross sections for elastic scattering α + 12C system.
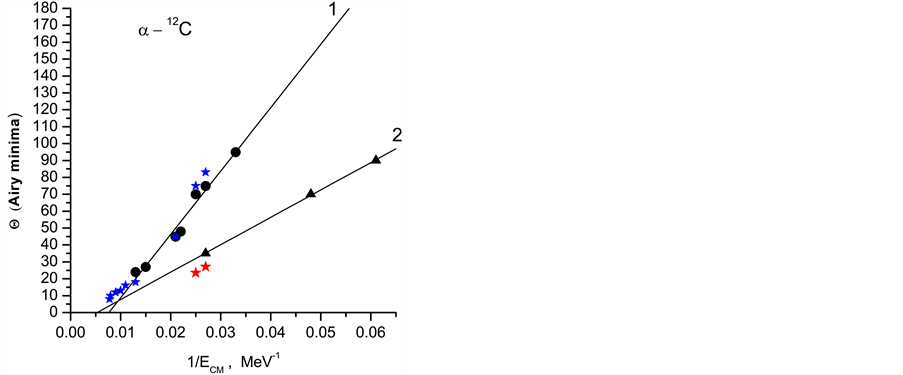
Figure 2. Positions of the Airy minima for α + 12C system.

Figure 3. Dispersion analysis of volume integrals of dispersive potentials for the α + 12C system.
liding nuclei, third test, has been shown in Figure 4. In this figure, the stars showed in the energies (center of mass) of 80 and 120 MeV in first Airy minima are the results that, clearly, are satisfactory.
The farside components calculated by us have been shown in
Figure 5. As we expected, the Airy minima shifts toward small degrees with
increasing energy of projectile. The radial dependence of the calculated total real
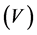 and the total imaginary
and the total imaginary
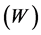 parts of the potentials at various laboratory energies have been shown in Figure 6.
parts of the potentials at various laboratory energies have been shown in Figure 6.
3. Conclusions
A semimicroscopic analysis of a set of experimental data of elastic
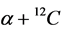 scattering was performed at several
scattering was performed at several
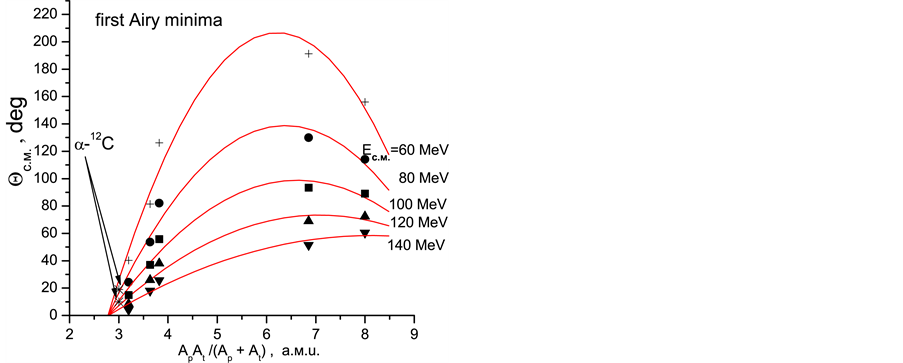
Figure 4. Estimated positions and approximating secondorder polynomials curves of first Airy minima versus the reduced mass.
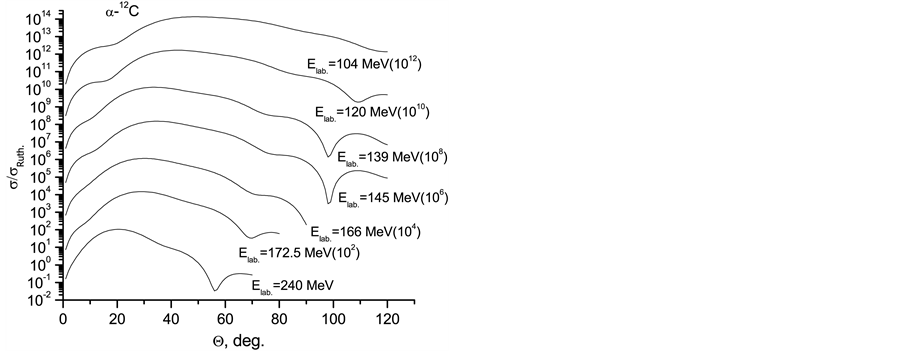
Figure 5. Calculated farsaid components for α + 12C system.
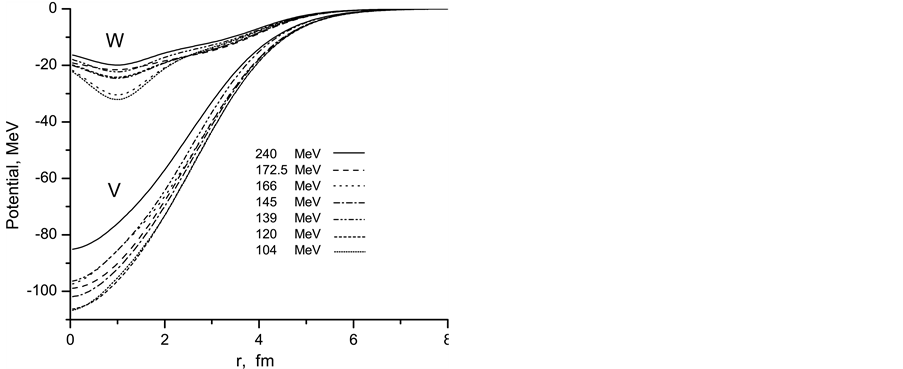
Figure 6. Found radial dependence of the total real and imaginary part of potential for α + 12C system at various laboratory energies.
laboratory energies. In this way, the microscopic calculation of static component of potential combines with the phenomenological calculation of the dynamical component of potential. In this model, the dynamical polarization potential is constructed on the basis of physically justified combinations of the volume and surface forms whose geometric parameters are assumed to be independent of energy.
The energy systematics of the positions of Airy minima was constructed, and it was shown that their positions depend linearly on the inverse center of mass energy. The energy dependence of the volume integrals was performed and has been shown that the dispersion relation is satisfied and agrees well with the results obtained within a phenomenological analysis. Using systematics of the positions of Airy minima with respect to reduced mass of colliding nuclei introduced by Goncharov and Izadpanah, has been shown that the found positions of the Airy minima satisfy the rule of the quadratical dependence of the position of the Airy minima on the reduced mass of colliding nuclei.
Using these three systematics, the parameters of the model potential at various energies have been determined unambiguously.
The obtained imaginary components are shown the meaningness of aberrations from its Woods-Saxon forms obtained using the phenomenological approach. This aberration occurs in the distances about 1 fm and one can be due to ignore of the dependence energy in this study.
Acknowledgments
We are grateful to C.А. Goncharov for enlightening comments and discussions.
References
- Satchler, G.R. (1983) Direct Nuclear Reactions. Clarendon, Oxford, 392.
- Mahaux, C., Ngo, H. and Satchler, G.R. (1986) Nuclear Physics A, 449, 354.http://dx.doi.org/10.1016/0375-9474(86)90009-6
- Bertsch, G., Borysowics, J., McManus, H. and Love, W.G. (1977) Nuclear Physics A, 284, 399.http://dx.doi.org/10.1016/0375-9474(77)90392-X
- Anantaraman, N., Toki, H. and Bertsch, G. (1983) Nuclear Physics A, 398, 269. http://dx.doi.org/10.1016/0375-9474(83)90487-6
- Khoa, D.T., Satchler, G.R. and von Oertzen, W. (1997) Physical Review C, 56, 954.http://dx.doi.org/10.1103/PhysRevC.56.954
- Goncharov, S.A. and Izadpanah, A. (2007) Physics of Atomic Nuclei, 70, 18. http://dx.doi.org/10.1134/S1063778807010036
- Ogloblin, A.A., Goncharov, S.A., Glukhov, Yu.A., et al. (2003) Physics of Atomic Nuclei, 66, 1478.http://dx.doi.org/10.1134/1.1601753
- Goncharov, S.A. and Izadpanah, A. (2007) Physics of Atomic Nuclei, 70, 1491. http://dx.doi.org/10.1134/S1063778807090037


