Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21671,8 pages DOI:10.4236/jmp.2012.38094
Semiclassical Husimi Function of Simple and Chaotic Systems
Departamento de Física e Matemática, Universidade Federal de São João Del Rei, Ouro Branco, Brazil
Email: adelcio@ufsj.edu.br
Received April 10, 2012; revised May 5, 2012; accepted May 31, 2012
Keywords: Classical Limit; Husimi Function; Quantum Chaos
ABSTRACT
We review the semiclassical method proposed in [1], a generalization of this method for n-dimensional system is presented. Using the cited method, we present an analytical method of obtain the semiclassical Husimi Function. The validity of the method is tested using Harmonic Oscillator, Morse Potential and Dikie’s Model as example, we found a good accuracy in the classical limit.
1. Introduction
Since early times of quantum theory, some quantization difficulties of non integrable systems were pointed by Einstein [2,3]. Recently, due to the pioneer discoveries of classically chaotic systems, the subject has yielded many interesting and important results both from the point of view of numerical models and (not as many) analytical proofs [4-6]. Also in this direction, the phenomena of scar [7-11] drew much attention. They showed that the Hamiltonians eigenfunctions of chaotic systems exhibit “scars” around unstable periodic orbit. An question that appears from those analyses is related to chaotic manifestation of classical chaos over the eigenfunctions in terms of quantities that are base independent [12-15]. In opposition, it has been reported that scars can exist in regions where there are no periodic orbits [16]. The search for classical “imprints” than the celebrated phenomena of scars on eigenfunctions of quantum systems with classical analog has also gained a lot of attention.
In the present contribution we begin by generalizing the semiclassical expansion [1] for n-dimensional system. The semiclassical expansion is built in a way that the first order wave function contains the classical dynamics for the system in question as completely as possible, in the sense that the dominant term is given only in terms of classical trajectories. Higher order contributions contain essentially quantum effects and make possible a precise identification of a classical behavior in the quantum dynamics for short times. We use this expansion to obtain the semiclassical Husimi distributions of simple systems.
This paper is organized as follows. In Sections 2 and 3 we present the method, we closely follow ref. [1]. In Section 4 we present a method of determining a semiclassical Husimi function. Section 7 contains conclusions.
2. The Semiclassical Expansion
Let us consider a classical one degree of freedom Hamiltonian of the form
 (1)
(1)
where p stands for the particle momentum and q for its position. We make a change of variables
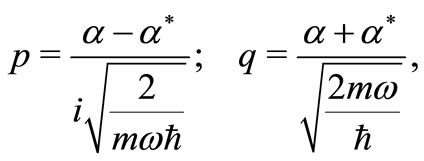 (2)
(2)
where
 (3)
(3)
The Hamiltonian can then be rewritten as
 (4)
(4)
with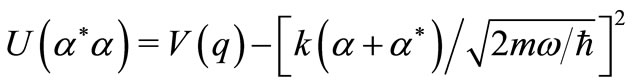 .
.
We can write 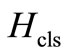 as a Taylor expansion,
as a Taylor expansion,

where .
.
The classical equations of motions are
 (5)
(5)
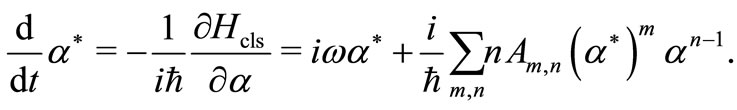 (6)
(6)
We choose the quantum Hamiltonian 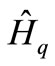 in order to have
in order to have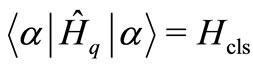 , if
, if 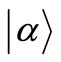 is a coherent field state.
is a coherent field state.
We make our semiclassical expansion around a quantum operator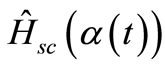 . The difference
. The difference
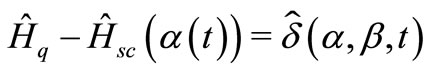
will be considered as a perturbation. We choose the semiclassical Hamiltonian, 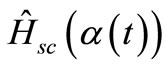 , in a way that for a coherent initial state, all expectation values of point classical observables will be precisely reproduced.
, in a way that for a coherent initial state, all expectation values of point classical observables will be precisely reproduced.
The semiclassical Hamiltonian which satisfies this condition is [1]:
 (7)
(7)
We can write the semiclassical evolution operator for an one degree of freedom, observing that
 (8)
(8)
where  is the well known displacement operator
is the well known displacement operator

and 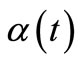 is given by 5, 6 and
is given by 5, 6 and 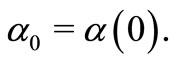
Thus, for the N dimensional case we have
 (9)
(9)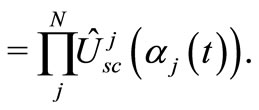
where, 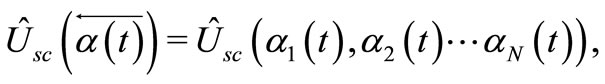 and
and 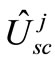 is the semiclassical evolution operator related to the k-th degree of freedom, note that it depends solely on
is the semiclassical evolution operator related to the k-th degree of freedom, note that it depends solely on 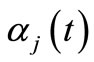 but in general we have
but in general we have
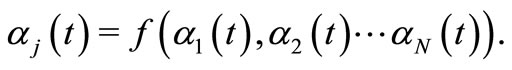
The phase 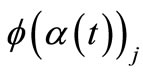 is given by
is given by
 (10)
(10)
where 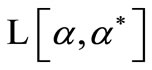 is the classical Lagrangian of the (independent) systems. In equation (9) we chose
is the classical Lagrangian of the (independent) systems. In equation (9) we chose  = 01, what can be done choosing a specific form of the semiclassical Hamiltonian, see [1]. A generalization for SU(2) algebra or for any subspace where coherent states can be included, is immediate. The action of the semiclassical evolution operator over a coherent state can always be written as [17]
= 01, what can be done choosing a specific form of the semiclassical Hamiltonian, see [1]. A generalization for SU(2) algebra or for any subspace where coherent states can be included, is immediate. The action of the semiclassical evolution operator over a coherent state can always be written as [17]
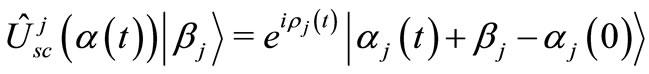 (11)
(11)
where
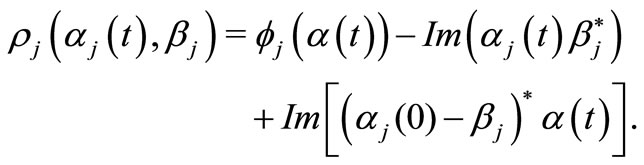
In general 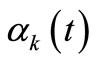 is a function of all
is a function of all . In the next sections we use the fact that the labels of coherent states follow the classical trajectories.
. In the next sections we use the fact that the labels of coherent states follow the classical trajectories.
3. Time Evolution
We consider a two degrees of freedom system, which the complete Hamiltonian is given by
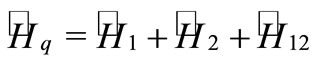 (12)
(12)
where  represent the autonomous dynamics of the degree of freedom 1 (2) and
represent the autonomous dynamics of the degree of freedom 1 (2) and 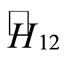 is their interaction. The semiclassical Hamiltonian has the following form2
is their interaction. The semiclassical Hamiltonian has the following form2
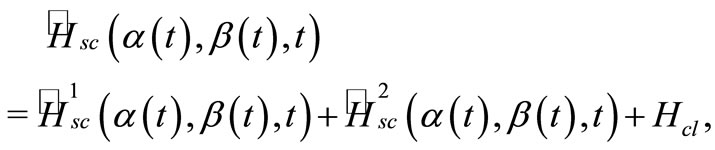 (13)
(13)
and by definition we have

As discussed in section II we rewrite the Hamiltonian (12) in the following form  where
where  . We make a perturbation expansion about
. We make a perturbation expansion about 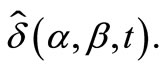 Using Schrödinger’s equation, where we will always use as initial state
Using Schrödinger’s equation, where we will always use as initial state 
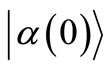 and
and  are coherent states. Thus, after some straightforward algebraic manipulations [1] we get
are coherent states. Thus, after some straightforward algebraic manipulations [1] we get
 (14)
(14)
where 
 The general problem of convergence of the serie (14) is an open problem. The convergence of the method was demonstrated for the quartic oscilator [1] and there is strong evidence of it for chaotic Dikie model [18], then it is reasonable to assume that the method is convergent at least to a group of non-integrable systems.
The general problem of convergence of the serie (14) is an open problem. The convergence of the method was demonstrated for the quartic oscilator [1] and there is strong evidence of it for chaotic Dikie model [18], then it is reasonable to assume that the method is convergent at least to a group of non-integrable systems.
4. Husimi’s Quantum Phase Space Distribution
The Q-function or Husimi’s function is, see refs. [4,19], defined by:
 (15)
(15)
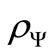 is a density operator, and
is a density operator, and 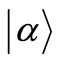 is the harmonic coherent state according to the definitions:
is the harmonic coherent state according to the definitions:
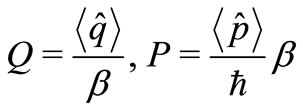 (16)
(16)
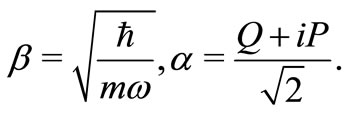 (17)
(17)
q and p are position and momentum operator respectively, and the mean is calculated in the coherent state  From this definition, we are able to write the Husimi function as
From this definition, we are able to write the Husimi function as
 (18)
(18)
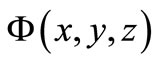 is the system Hamiltonian eigenfunction, and
is the system Hamiltonian eigenfunction, and  is the harmonic coherent state in three dimensions , it is given by
is the harmonic coherent state in three dimensions , it is given by
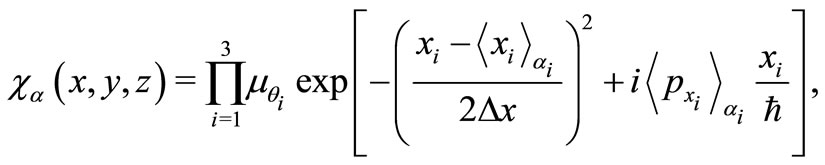 (19)
(19)
where ,
,  ,
, 
 is the momentum related with
is the momentum related with , and
, and
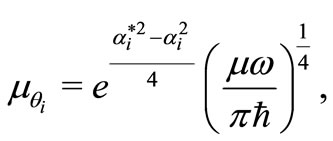 (20)
(20)
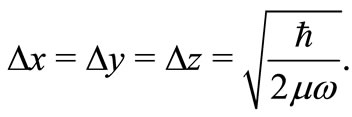 (21)
(21)
For the simplest case of the Harmonic Oscillator, using equation [15], the Husimi Function for an eigenstate, n, can be written as:
 (22)
(22)
In terms of Q and P, we have
 (23)
(23)
4.1. Husimi Function for the Morse Potential
The Morse potential is used to model diatomic molecules, it is defined as :
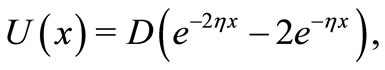 (24)
(24)
where
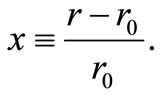 (25)
(25)
The  values are the equilibrium position of the center of mass,
values are the equilibrium position of the center of mass, 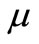 is the reduced mass of the two atoms and r is the distance between the atoms. The constant D defines the minimum value o the potential wich is
is the reduced mass of the two atoms and r is the distance between the atoms. The constant D defines the minimum value o the potential wich is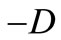 . The constant
. The constant  determines the potential range. The Hamiltonian that describes the center of mass can be written as:
determines the potential range. The Hamiltonian that describes the center of mass can be written as:
 (26)
(26)
where L is the angular momentum. The time independent Schrödinger equation is:
 (27)
(27)
We can write the wavefunction as
 (28)
(28)
where  is the spherical harmonics:
is the spherical harmonics:
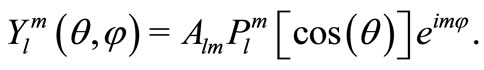 (29)
(29)
For L = 0 case we find the eigenvalues:
 (30)
(30)
where 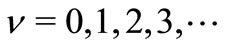
 and
and
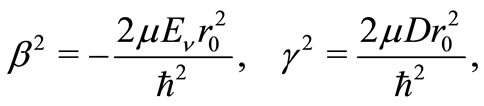 (31)
(31)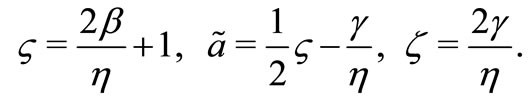
and for the eigenfunctions:
 (32)
(32)
A1 is fixed by normalization, 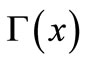 is the gamma function.
is the gamma function.
Following the definition (20), we obtain the Husimi the Function [20] as
 (33)
(33)
where . The exact Husimi function is obtained by numerically integration of (33).
. The exact Husimi function is obtained by numerically integration of (33).
4.2. Semiclassical Husimi’s Function
The semiclassical expansion, as defined above, gives us the time evolution of a quantum state as a perturbative expansion. An eigenstate has only a time dependent phase as its dynamics. The nearest semiclassical scenario we can build is to choose a coherent state with the same energy. The time dependence can be eliminated by a time integration, i.e., a mean in time. This integration can be justified noting that as we are dealing with eigenstates we have not time precision. Under this considerations we may write the semiclassical Husimi function as
 (34)
(34)
The states  and
and  are coherent states of the harmonic oscillator.
are coherent states of the harmonic oscillator. 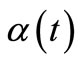 is defined as
is defined as
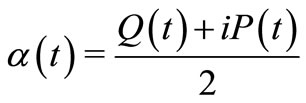 and
and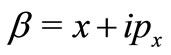 where x and
where x and 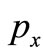 are parameters of the Husimi Function,
are parameters of the Husimi Function, 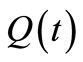 and
and  correspond to the classical canonical conjugate pairs redefined as in Equations (16) and (17). In case of classical mixed dynamics we must perform a mean considering all possible initial condition with the same specific energy. We should also use adequate coherent state base for each algebra. This semiclassical Husimi function is calculated by taking a long time mean, formally we write it as
correspond to the classical canonical conjugate pairs redefined as in Equations (16) and (17). In case of classical mixed dynamics we must perform a mean considering all possible initial condition with the same specific energy. We should also use adequate coherent state base for each algebra. This semiclassical Husimi function is calculated by taking a long time mean, formally we write it as
 (35)
(35)
As we known, classically chaotic systems stay longer times [4] near a stable or unstable periodic orbit. In our numerical calculation it means that this region has a huge contribution in the mean (35) or (34). Easily we can show that
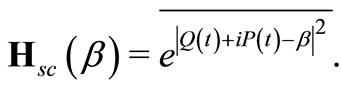 (36)
(36)
The semiclassical Husimi distributions is determined by the classical trajectory solely. In general the semiclassical Husimi function is obtained by numerical methods, it is the case of all chaotic model.
4.2.1. Morse Potential
For the Morse potential, with L = 0, we obtain the classical trajectory [20] as:
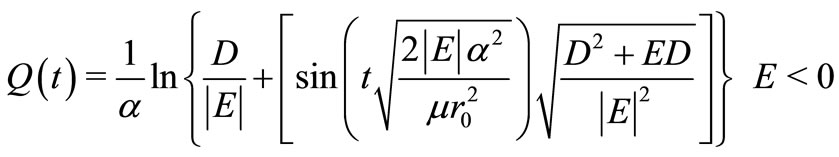 (37)
(37)
We also have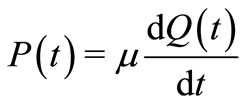 , and we can choose
, and we can choose 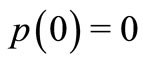 and choosing the energy as
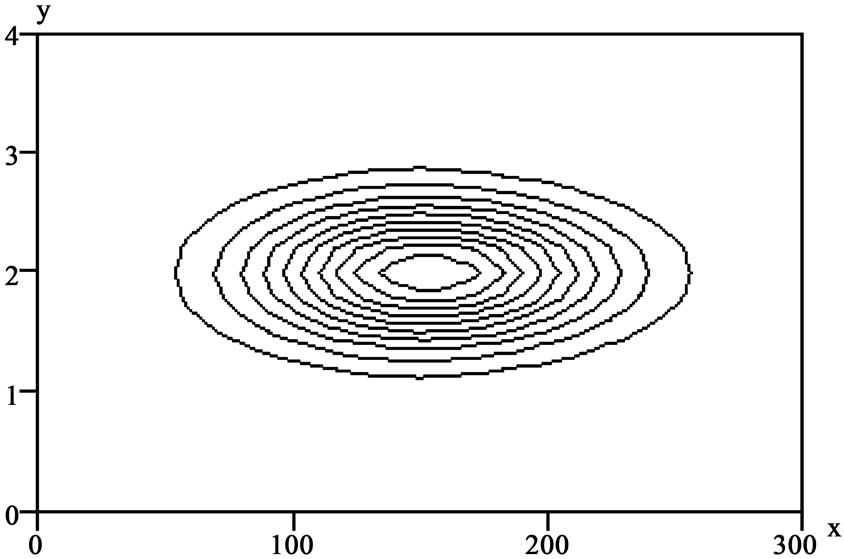
and choosing the energy as 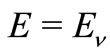 into (36) to obtain the semiclassical Husimi function. The mean (35) is obtained by a numerical integration. In Figure 1 we show the approximated semiclassical Husimi for the Morse potential with the parameters of the
into (36) to obtain the semiclassical Husimi function. The mean (35) is obtained by a numerical integration. In Figure 1 we show the approximated semiclassical Husimi for the Morse potential with the parameters of the 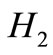 molecule, for
molecule, for . In Figure 2 we have the exact result, Figure 3 shows the semiclassical Husimi function for n = 1 and Figure 4 the exact result, details about exact calculation can be found in ref. [20]. As we can observe in this Figures 1-4, the semiclassical Husimi function does not reproduce exactly the Husimi function, but it regards some similarities. Notice that the main region is located in the same phase space area for the exact and semiclassical Husimi function.
. In Figure 2 we have the exact result, Figure 3 shows the semiclassical Husimi function for n = 1 and Figure 4 the exact result, details about exact calculation can be found in ref. [20]. As we can observe in this Figures 1-4, the semiclassical Husimi function does not reproduce exactly the Husimi function, but it regards some similarities. Notice that the main region is located in the same phase space area for the exact and semiclassical Husimi function.
4.2.2. Harmonic Oscillator
Now consider the Harmonic potential with a natural frequency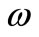 , its classical dynamics is given by
, its classical dynamics is given by

Figure 1. semiclassical Husimi function for the Morse Potential, 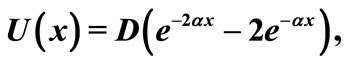 where
where  We have used the experimental hydrogen molecule values,
We have used the experimental hydrogen molecule values,  and
and  The principal quantum number n = 0 and the angular momentum L = 0. The x axis is related to the position, r, as
The principal quantum number n = 0 and the angular momentum L = 0. The x axis is related to the position, r, as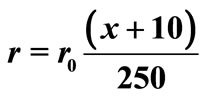 , the momentum p is related to the y axis variable as
, the momentum p is related to the y axis variable as  We have used
We have used 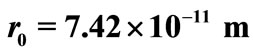 and
and  rad/s.
rad/s.
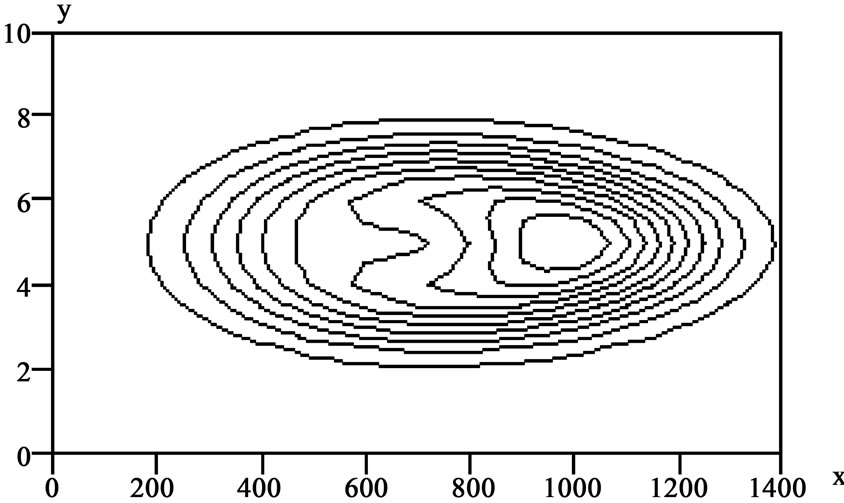
Figure 3. Semiclassical Husimi function for the Morse Potential, 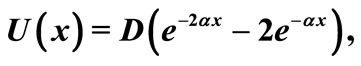 where
where 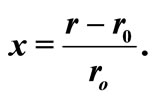 We have used the experimental hydrogen molecule values,
We have used the experimental hydrogen molecule values,  and
and  The principal quantum number n=1 and the angular momentum L = 0. The x axis is related to the position, r, as
The principal quantum number n=1 and the angular momentum L = 0. The x axis is related to the position, r, as  the momentum p is related to the y axis variable as
the momentum p is related to the y axis variable as 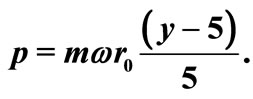 We have used
We have used  and
and  rad/s.
rad/s.
 (38)
(38)
and
 (39)
(39)
We redefined Q and P in a such way that the Hamiltonian can be written as
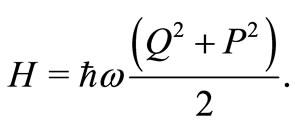 (40)
(40)
Substituting (38) and (39) into (36) we obtain a semiclassical Husimi Function for the Harmonic oscillator with an energy . Without any loss of generality we can use
. Without any loss of generality we can use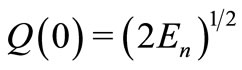 , and
, and . In Figure 5 we show the approximated and exact Husimi function for the Harmonic potential for n = 5. Figure 6 shows the semiclassical and exact Husimi function for n = 100. Again the mean (35) is obtained numerically.
. In Figure 5 we show the approximated and exact Husimi function for the Harmonic potential for n = 5. Figure 6 shows the semiclassical and exact Husimi function for n = 100. Again the mean (35) is obtained numerically.
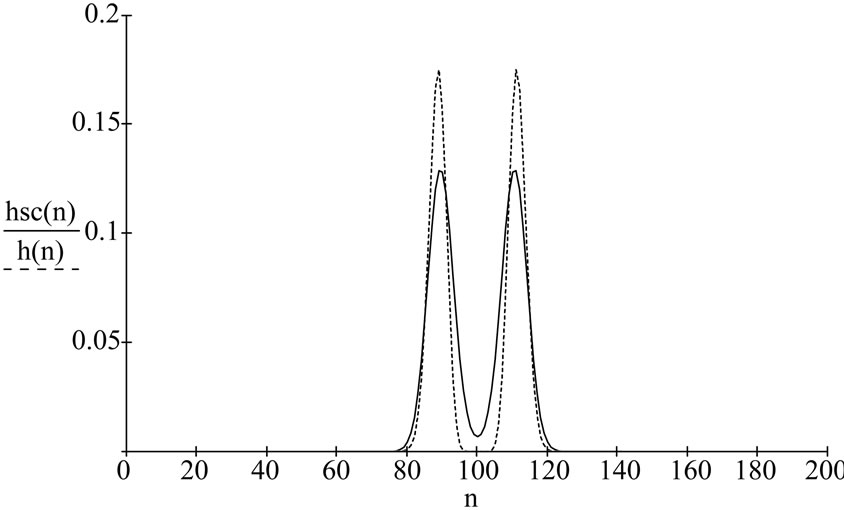
Figure 5. Full line shows a cross section of Husimi function for the harmonic potential for p = 0. The principal quantum number n = 5. The x axis is related to the position. Dotted line, correspondent semiclassical Husimi function.

Figure 6. Full line shows a cross section of Husimi function for the harmonic potential for p = 0. The principal quantum number n = 100. The x axis is related to the position. Dotted line, correspondent semiclassical Husimi function.
4.2.3. Dickie Model
In the Figures 1 to 7 we have used classical integrable models, although that our approach is also useful for non-integrable thus let us take a look in Dikie model [21], his quantum Hamiltonian is
 (41)
(41)
where
 (42)
(42)
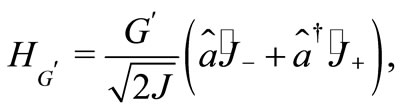 (43)
(43)
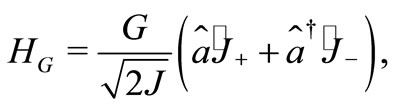 (44)
(44)
 is the harmonic oscillator natural frequency,
is the harmonic oscillator natural frequency,  is precession frequency, G and
is precession frequency, G and 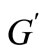 are coupling constants.
are coupling constants.
In the harmonic term of (42) 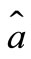 and
and  are bosonic anihilation and creation operators of harmonic oscillator,
are bosonic anihilation and creation operators of harmonic oscillator,  is the angular momentum operator in k direction and
is the angular momentum operator in k direction and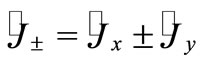 . In order to obtain the Semiclassical Husimi function for the Dickie model we have to integrate numerically the corresponding classical equations of motion and calculate the mean (35).
. In order to obtain the Semiclassical Husimi function for the Dickie model we have to integrate numerically the corresponding classical equations of motion and calculate the mean (35).
In Figure 7 we show the semiclassical Wigner function of ground state of Dickie model [21] in an integrable regime. In Figure 8 we have the semiclassical Wigner function for Dickie model in a non-integrable regime. Comparing with exact Wigner3 function that can be found in ref. [21], we see that semiclassical Husimi function contains the main information about the exact one. A detailed semiclassical analysis of Dickie’s model can be found in [18,22]. In [18] they show a numerical evidence of the expansion convergence for the Dickie’s model.
4.2.4. The Quality of the Approximation
Now we quantify the quality of the approximation using the function , which is defined as
, which is defined as
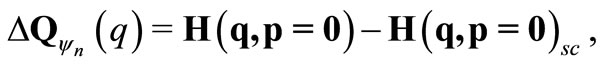 (45)
(45)
where H is the exact Husimi function and Hsc is the semiclassical Husimi function. Due to the symmetry we have chosen p = 0. As we increase the principal quantum number (n), in the classical limit, we hope we have . In order to see the classical limit, let us define the function
. In order to see the classical limit, let us define the function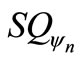 , which is
, which is
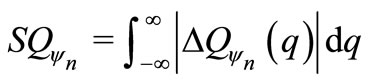 (46)
(46)
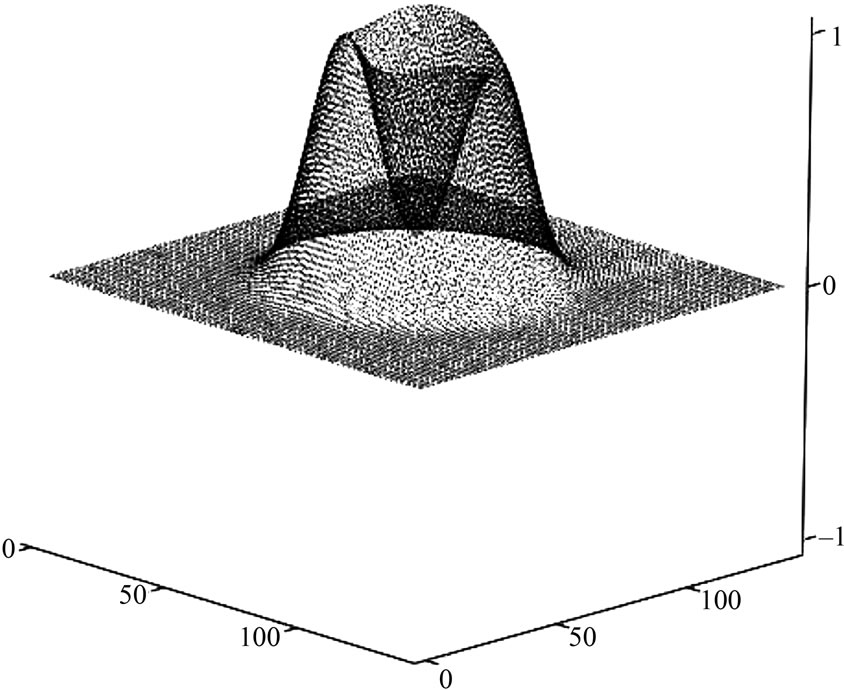
Figure 7. Semiclassical Wigner function for the fundamental state of Dickie model where ,
,  ,
, .
.
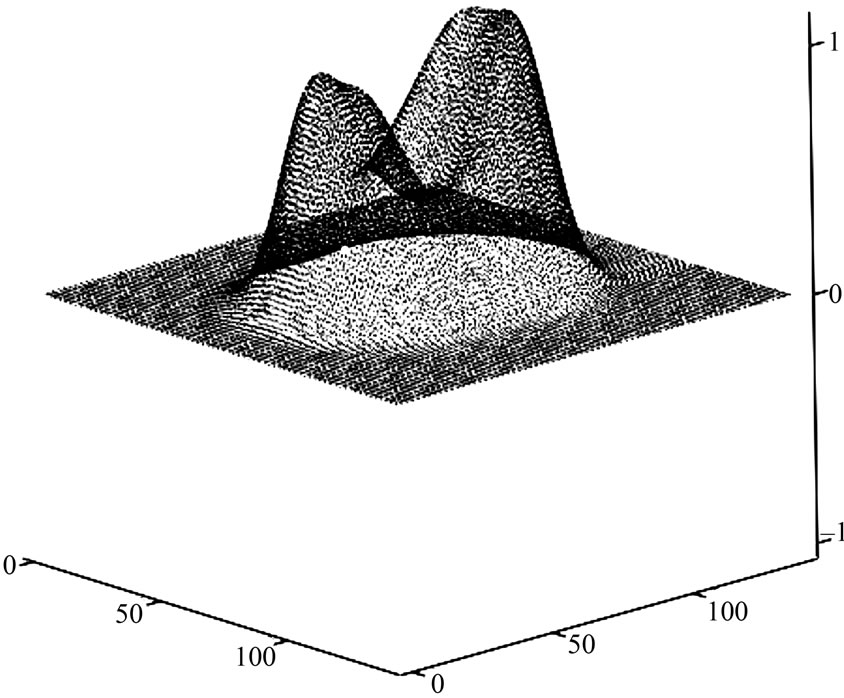
Figure 8. Semiclassical Wigner function for the fundamental state of Dickie model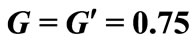 .
.
Suppose we have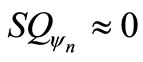 . It means that quantum description of the state
. It means that quantum description of the state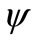 , in the Husimi’s representation, is almost contained in the semiclassical one. In spite of that we can say that the quantum classical difference becomes smaller, as expected. Of course it does not mean that we have no quantum features4, it only means that Husimi is not a good observable for this situation [23]. Figure 9 shows
, in the Husimi’s representation, is almost contained in the semiclassical one. In spite of that we can say that the quantum classical difference becomes smaller, as expected. Of course it does not mean that we have no quantum features4, it only means that Husimi is not a good observable for this situation [23]. Figure 9 shows  say that the approximation works better as we increase the principal quantum number, as expected. From these figures we may conclude that the classical ingredient is very strong on the state formation of regular systems. In other words,those figures suggests that scars are essentially a classical manifestation in the quantum system since the building blocks of the semiclassical Husimi are classical trajectories.
say that the approximation works better as we increase the principal quantum number, as expected. From these figures we may conclude that the classical ingredient is very strong on the state formation of regular systems. In other words,those figures suggests that scars are essentially a classical manifestation in the quantum system since the building blocks of the semiclassical Husimi are classical trajectories.
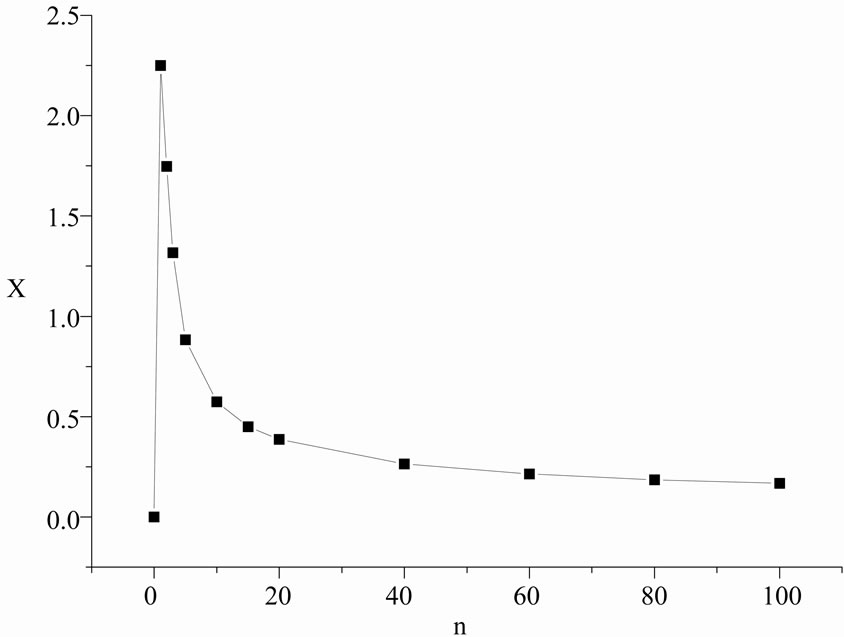
Figure 9. SQ function for the harmonic oscillator. X axis corresponds to the principal quantum number n.
5. Conclusion
We show that the semiclassical Husimi function reproduces the major features of the quantum one, in the particular harmonic case, we show that the first semiclassical term is able to reproduce the Husimi function with a increasing accuracy as we increase the principal quantum number n. We must remark that there is no demonstration that would suggest an existence of the limit procedure which turns quantum corrections less important in terms of the proposed semiclassical expansion. The building blocks of semiclassical Husimi Function are the classical trajectories, then we can conclude that classical periodic orbits (stable or unstable) contribute with higher weight. The fidelity decay rate has a gaussian regime that is only perturbation potential dependent, although its validity is determined by .
.
6. Acknowledgements
The author is grateful to Fapesb for partial financial support. The author also acknowledge, A. R. Bosco de Magalhaes, M. C. Nemes, Fernanda Alves de Oliveira for helpful comments.
REFERENCES
- A. C. Oliveira and M. C. Nemes and K. M. F. Romero, “Quantum Time Scales and the Classical Limit: Analytic Results for Some Simple Systems,” Physical Review E, Vol. 68, No. 3, 2003, Article ID: 036214. doi:10.1103/PhysRevE.68.036214
- A. Einstein, “Zum Quantensatz von Sommerfeld und Epstein on the Quantum Theory of Sommerfeld and Epstein,” Deutsche Physikalische Gesellschaft Verhandlungen, Vol. 19, 1917, p. 82.
- M. A. M. de Aguiar, “Einstein and the quantum chaos theory,” Revista de Ensino de Física, Vol. 27, 2005, p. 101.
- M. C. Gutzwiller, “Chaos in Classical and Quantum Mechanics,” Spring-Verlg, New York, 1990.
- H. J. StockmannHaake, “Quantum Chaos an Introduction,” Cambridge University Press, New York, 1999.
- F. Haake, “Quantum Signatures of Chaos,” SpringerVerlag, Berlin, 2004.
- S. W. McDonald and A. N. Kaufmann, “Spectrum and Eigenfunctions for a Hamiltonian with Stochastic Trajectories,” Physical Review Letters, Vol. 42, No. 18, 1979, pp. 1189-1191. doi:10.1103/PhysRevLett.42.1189
- E. B. Bogomolny, “Fine structure of the wave functions of quantum systems,” JETP Letters, Vol. 44, No. 9, 1986, pp. 561-565.
- E. B. Bogomolny, “Smoothed Wave Functions of Chaotic Quantum Systems,” Physica D, Vol. 31, No. 2, 1988, pp. 169-189. doi:10.1016/0167-2789(88)90075-9
- E. J. Heller, “Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits,” Physical Review Letters, Vol. 53, No. 16, 1984, pp. 1515- 1518. doi:10.1103/PhysRevLett.53.1515
- E. J. Heller, “Quantum Chaos and Statistical Nuclear Physics,” Springer, Berlin, 1983.
- L. Benet and T. H. Seligman and H. A. Weidenmuller, “Quantum signatures of Classical Chaos: Sensitivity of Wave Functions to Perturbations,” Physical Review Letters, Vol. 71, No. 4, 1993, pp. 529-532. doi:10.1103/PhysRevLett.71.529
- M. Srednicki and F. Stiernelof, “Gaussian fluctuations in chaotic eigenstates,” Journal of Physics A, Vol. 29, No. 18, 1996, p. 5817. doi:10.1088/0305-4470/29/18/013
- L. Benet and F. M. Izrailev and T. H. Seligman and A. Suarez-Moreno, “Semiclassical properties of eigenfunctions and Occupation Number Distribution for a model of Two Interacting Particles,” Physics Letters A, Vol. 277, No. 2, 2000, pp. 87-93. doi:10.1016/S0375-9601(00)00692-7
- L. Benet, et al., “Fluctuations of wavefunctions about their classical average,” Journal of Physics A, Vol. 36, No. 5, 2003, p. 1289. doi:10.1088/0305-4470/36/5/307
- P. Bellomo and T. Uzer, “Quantum scars and classical ghosts,” Physical Review A, Vol. 51, No. 2, 1995, pp. 1669-1672. doi:10.1103/PhysRevA.51.1669
- W. Zhang, H. Feng and R. Gilmore, “Coherent states: Theory and some applications,” Reviews of Modern Physics, Vol. 62, No. 4, 1990, pp. 867-927. doi:10.1103/RevModPhys.62.867
- M. Reis and M. C. Nemes and J. G. P. de Faria, “Semiclassical corrections to the large-N limit of Dicke’s model,” Physical Review E, Vol. 78, No. 3, 2008, Article ID: 036220. doi:10.1103/PhysRevE.78.036220
- W. P Scleichr, “Quantum Optics in Pahse Space,” WileyVCC, Berlin, 2001.
- A. C. Oliveira and M. C. Nemes, “Classical Structures in the Husimi Distributions of Stationary States for H2 and HCl Molecules in the Morse Potential,” Physica Scripta, Vol. 64, No. 4, 2001, p. 279. doi:10.1238/Physica.Regular.064a00279
- M. C. Nemes, K. Furuya, G. Q. Pelegrino, A. C. Oliveira, M. Reis and L. SanzM, “Quantum entanglement and fixed point Hopf bifurcation,” Physics Letters A, Vol. 354, No. 1-2, 2006, pp. 60-66. doi:10.1016/j.physleta.2006.01.028
- K. M. F. Romero, M. C. Nemes, J. G. P. de Faria and A. F. R. de T. Piza, “Sensitivity to Initial Conditions in Quantum Dynamics: An Analytical Semiclassical Expansion,” Physics Letters A, Vol. 327, No. 2-3, 2004, pp. 129-137. doi:10.1016/j.physleta.2004.04.070
- A. C. Oliveira and J. G. P. de Faria and M. C. Nemes, “Quantum-Classical Transition of the Open Quartic Oscillator: The role of the environment,” Physical Review E, Vol. 73, No. 4, 2006, Article ID: 046207. doi:10.1103/PhysRevE.73.046207
NOTES
1 refers to j-th system.
refers to j-th system.
2 represents the semiclassical Hamiltonian in the subspace 1, and
represents the semiclassical Hamiltonian in the subspace 1, and  represents the semiclassical Hamiltonian in the subspace 2.
represents the semiclassical Hamiltonian in the subspace 2.
3For stationary states semiclassical Wigner function and semiclassical Hunimi function are identical.
4For example, the Wigner function can be negative at some point while the semiclassical Husimi function and the exact one are almost identical.