Journal of Modern Physics
Vol.3 No.5(2012), Article ID:19267,8 pages DOI:10.4236/jmp.2012.35057
A New Approach to Mesons’ States and Their Dependence on Spin and Isospin: A Mathematical Study
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani1983@yahoo.com
Received November 8, 2011; revised December 1, 2011; accepted February 12, 2012
Keywords: Meson; Spin; Isospin; Quark; Antiquark
ABSTRACT
A meson comprises a quark and an antiquark moving under the impact of a combination of color, oscillating, and confinement potentials. Considering the fact that the quarks are particles with spin 0.5, there is also a spin-spin interaction potential. Moreover, the quarks d and u have isospin; the potentials of isospin-isospin effect and spin-isospin effect should be taken into consideration. Through comparing the obtained meson spectra with the values calculated through this model, it can be determined whether the quark and antiquark constituting mesons are singlet or triplet in terms of spin and isospin. Exploiting this method, the configuration of spin and isospin states relating to each meson can be achieved.
1. Introduction
The mesons are bosons having spin of zero or one, and composed of quark and antiquark that are fermions with spin 0.5. In the mesons, the potential between quark and antiquark can be considered through various methods; however, the best model is a potential including all the properties of quark-antiquark pair. In this paper, the interaction we consider is the interaction of oscillations between these two particles and confinement potential. Furthermore, the color-force potential is created by replacing gluons between quark and antiquark so that each quark is affected by a force applied by another quark. Regarding the above-mentioned descriptions, the central potential is considered as the following form approved by laboratory evidences [1-5]:
 (1)
(1)
where , and
, and  is the distance between quark and antiquark.
is the distance between quark and antiquark.
The short-range potential (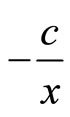 ) is similar to the attractive Coulomb potential, and derived from the interaction between quark and antiquark in short distances; it originates in the color charge. In fact, this term comes from the displacement of gluon. Generally, the color potential is as follows [1-4]:
) is similar to the attractive Coulomb potential, and derived from the interaction between quark and antiquark in short distances; it originates in the color charge. In fact, this term comes from the displacement of gluon. Generally, the color potential is as follows [1-4]:
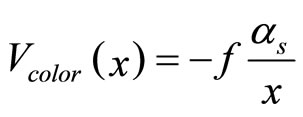 (2)
(2)
where f is the color factor and dependent on the color of interaction’s quarks. It is easily calculated that 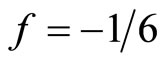 for the color-octet state, and f = 4/3 for the color-singlet state. The strong-coupling coefficient (
for the color-octet state, and f = 4/3 for the color-singlet state. The strong-coupling coefficient ( ) is very small [1-5]. The potential
) is very small [1-5]. The potential 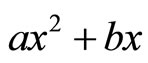 indicates either the role of confinement potential or the role of a quark’s oscillations in relation to another quark in the distance x; actually, this expression is a constraining potential. With regards to the term bx, detaching quarks from hadrons is impossible, and produces new pairs of quark and antiquark (that is why the free quark is never found in nature). It can be assumed that the color field’s lines of force are stretched by the gluon-gluon interaction, and these lines form threadlike bands. The stretching of these threads is related to the potential energy of
indicates either the role of confinement potential or the role of a quark’s oscillations in relation to another quark in the distance x; actually, this expression is a constraining potential. With regards to the term bx, detaching quarks from hadrons is impossible, and produces new pairs of quark and antiquark (that is why the free quark is never found in nature). It can be assumed that the color field’s lines of force are stretched by the gluon-gluon interaction, and these lines form threadlike bands. The stretching of these threads is related to the potential energy of 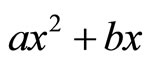 so that increasing the distance causes this energy to grow; finally, it reaches to the extent that is appropriate for producing the pair
so that increasing the distance causes this energy to grow; finally, it reaches to the extent that is appropriate for producing the pair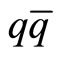 ; accordingly, there are two threads smaller than the first long thread. The potentials of Equation (1) centrally define the interaction between two subjects. In this investigation, the heavy mesons are considered; subsequently, the Schrödinger equation is utilized and the meson system’s wave function is achieved; afterwards, the isospin-spin and isospin-isospin potentials are perturbationally input to the equation, and the contribution of each meson’s spectrum is calculated. Actually, the mass splitting in some hadron layers may be dependent on various factors; hence, the mentioned hyperfine splitting can be highly effective. Therefore, first, the spinspin and isospin-isospin potentials [6-11] can be applied as follows:
; accordingly, there are two threads smaller than the first long thread. The potentials of Equation (1) centrally define the interaction between two subjects. In this investigation, the heavy mesons are considered; subsequently, the Schrödinger equation is utilized and the meson system’s wave function is achieved; afterwards, the isospin-spin and isospin-isospin potentials are perturbationally input to the equation, and the contribution of each meson’s spectrum is calculated. Actually, the mass splitting in some hadron layers may be dependent on various factors; hence, the mentioned hyperfine splitting can be highly effective. Therefore, first, the spinspin and isospin-isospin potentials [6-11] can be applied as follows:
 (3)
(3)
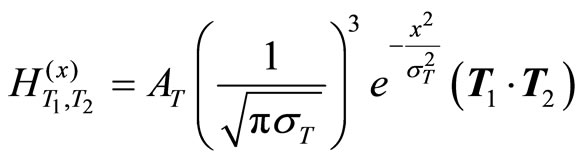 (4)
(4)
Through combining the spin-spin and isospin-isospin interaction potentials, a new spin-isospin interaction potential is obtained. Consequently, considering Equations (3) and (4), the spin-isospin potential can be written as the below form:
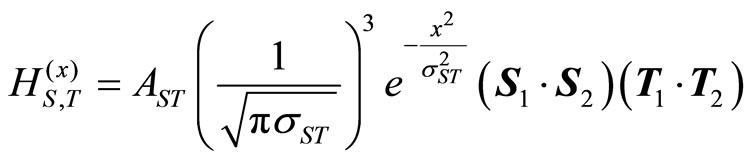 (5)
(5)
where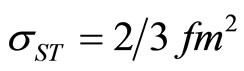 ,
, 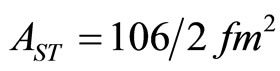 [12-14].
[12-14].
The perturbation potential of equation is the sum of the interaction potentials of Equations (3), (4), and (5). First, the Schrödinger equation is solved for the potential of Equation (1); then, the perturbational potential is considered, and the mesons’ spectrum is obtained. By comparing the mass obtained for each meson, it can be determined whether each meson’s constituent quarks are singlet or triplet. Each meson’s state function can be achieved through this method.
Regarding the interaction potential of Equation (1) and the hyperfine interaction potential of Equations (3) and (4), the interaction potential of a meson containing a quark and an antiquark can be considered as follows [12]:
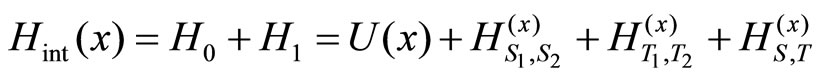 (6)
(6)
where 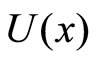 is the potential of Equation (1).
is the potential of Equation (1).
2. The Analytic Solution to the Schrödinger Radial Equation by the Interaction Potential of Equation (1)
To solve the Schrödinger radial equation by the non-perturbational potential  of Equation (1), we propose a method which can be easily exploited for the doublet systems, particularly, such as mesons consisting of a quark
of Equation (1), we propose a method which can be easily exploited for the doublet systems, particularly, such as mesons consisting of a quark 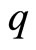 and an antiquark
and an antiquark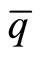 . Hence, such system’s Schrödinger equation is the motion of a particle with regard to another particle:
. Hence, such system’s Schrödinger equation is the motion of a particle with regard to another particle:
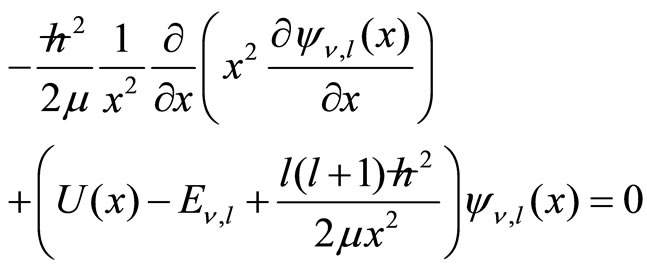 (7)
(7)
where the reduced quark-antiquark mass v is the node number (zero is on the axis) [12], and l is the orbital quantum number of a particle’s motion in relation to another particle. If we select
v is the node number (zero is on the axis) [12], and l is the orbital quantum number of a particle’s motion in relation to another particle. If we select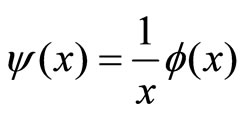 Equation (7) is briefed as follows:
Equation (7) is briefed as follows:
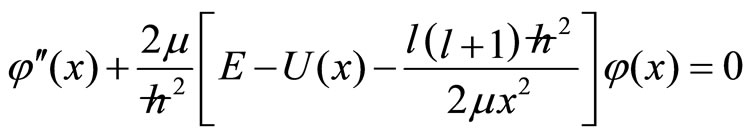 (8)
(8)
 can be obtained through Equation (8). By assuming
can be obtained through Equation (8). By assuming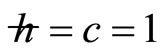 , and proposing
, and proposing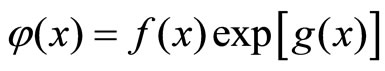 , the computation of
, the computation of 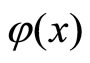 can be pursuit. Herein, the functions
can be pursuit. Herein, the functions 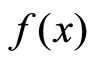 and
and  can be introduced as the following form:
can be introduced as the following form:
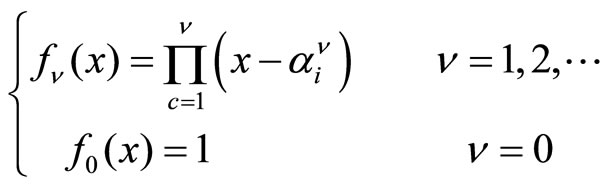 (9)
(9)
where 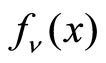 is similar to the Hermite polynomials, and the multiplier
is similar to the Hermite polynomials, and the multiplier 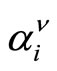 is achieved according to the potential coefficients.
is achieved according to the potential coefficients.
But, the polynomial  is determined with regard to the type of quark-antiquark interaction potential. In this special problem, considering the potential of Equation (1), it is written as follows:
is determined with regard to the type of quark-antiquark interaction potential. In this special problem, considering the potential of Equation (1), it is written as follows:
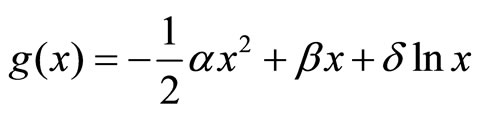 (10)
(10)
Regarding the proposed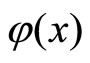 , it is concluded that:
, it is concluded that:
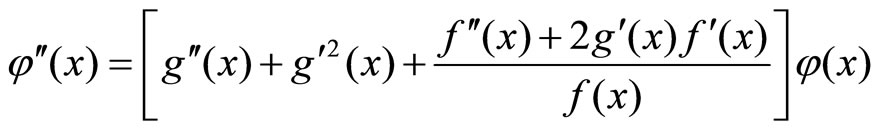 (11)
(11)
The intensity coefficients of interaction potential of Equation (8) equal ,
, 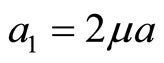 ,
, 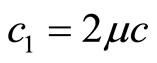 , and
, and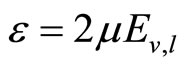 .
.
Now, the problem is solved for 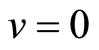 [12]. Using the functions
[12]. Using the functions 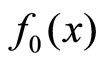 and
and , and the potential
, and the potential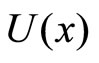 , it is briefly written as follows:
, it is briefly written as follows:
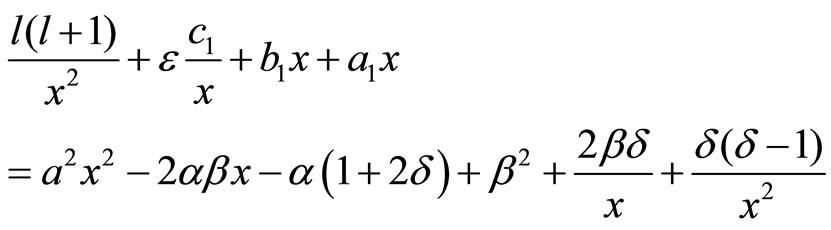 (12)
(12)
By means of Equation (12), through a simple calculation, and considering the fact that the powers of x ( ) are linear independent, the different powers of x can be equaled. Accordingly, an equation of the potential coefficients of
) are linear independent, the different powers of x can be equaled. Accordingly, an equation of the potential coefficients of ,
, 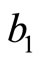 , and
, and 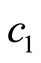 is achieved; furthermore, the equation of the coefficients of potential, energy, and mass of quarks can be acquired [13, 14].
is achieved; furthermore, the equation of the coefficients of potential, energy, and mass of quarks can be acquired [13, 14].
The characteristic value of energy for the state 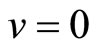 and the momentum l can be obtained as the below form:
and the momentum l can be obtained as the below form:
 (13)
(13)
The non-perturbed wave function for the state  equals:
equals:
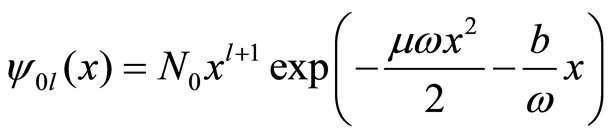 (14)
(14)
Secondly, we have 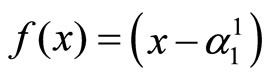 for the state
for the state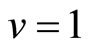 . The function
. The function 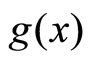 is defined in Equation (10). Now, the energy for the first excited state
is defined in Equation (10). Now, the energy for the first excited state 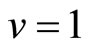 and the angular momentum l equals:
and the angular momentum l equals:
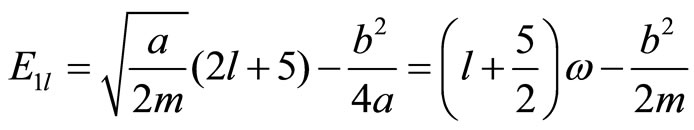 (15)
(15)
The non-perturbed characteristic function for the first excited state is:
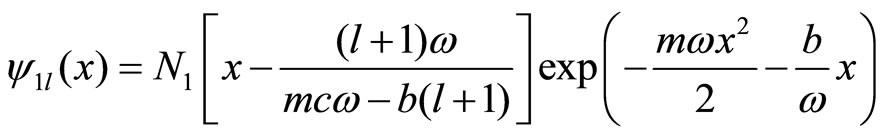 (16)
(16)
Through this method, the characteristic functions of higher states can be achieved. The states of  can be easily obtained. Consequently, the Schrödinger equation, the characteristic values of
can be easily obtained. Consequently, the Schrödinger equation, the characteristic values of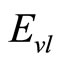 , and the characteristic functions of
, and the characteristic functions of  for the non-perturbed state are accurately and analytically achieved. Now, through selecting the non-confinement potentials of Equation (6) as the perturbational potentials, we can determine whether the existing states of mesons are singlet or triplet. The perturbational wave function is obtained due to the perturbational interaction of Equation (6). In the firstorder approximation, it equals as the following form:
for the non-perturbed state are accurately and analytically achieved. Now, through selecting the non-confinement potentials of Equation (6) as the perturbational potentials, we can determine whether the existing states of mesons are singlet or triplet. The perturbational wave function is obtained due to the perturbational interaction of Equation (6). In the firstorder approximation, it equals as the following form:
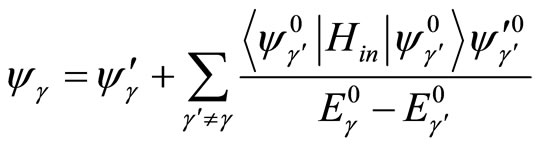 (17)
(17)
By briefing the above result, the perturbational energy levels 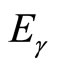 can be acquired. The first-order correction of energy equals
can be acquired. The first-order correction of energy equals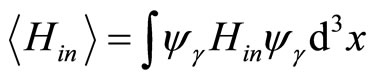 . Also, the higher corrected energy levels can be achieved using the above method. Subsequently, the meson spectrum equals the sum of quark and antiquark masses, the energy of interaction between them, and the perturbational energy of internal interaction
. Also, the higher corrected energy levels can be achieved using the above method. Subsequently, the meson spectrum equals the sum of quark and antiquark masses, the energy of interaction between them, and the perturbational energy of internal interaction 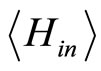 [15-17]:
[15-17]:
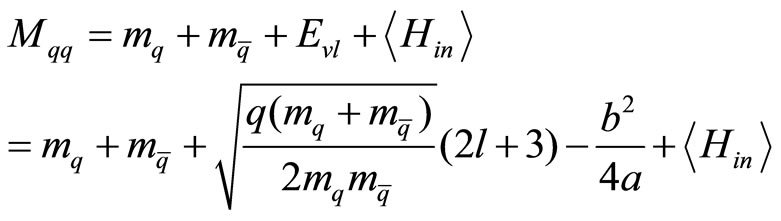 (18)
(18)
Equation (18) indicates that the quark and antiquark masses are dependent on the potential coefficients a and b.
3. The Computation of Perturbational Interactions
3.1. The Effect of Perturbational Energy Resulting from the Effect of Spin-Spin Potential
Since quarks are fermions with spin 0.5, the quarks’ spin effect must be considered to accurately study the interactions. If it is assumed that 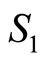 and
and 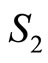 are respectively quark’s spin and antiquark’s spin, the perturbation effect of spin-spin potential can be considered with regards to Equation (3) [18-24]. The mesons’ total spin must be considered as the singlet state (
are respectively quark’s spin and antiquark’s spin, the perturbation effect of spin-spin potential can be considered with regards to Equation (3) [18-24]. The mesons’ total spin must be considered as the singlet state (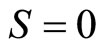 ) or triplet state (
) or triplet state (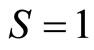 ). In this state, the above potential state is considered as the perturbation. For the ground state (
). In this state, the above potential state is considered as the perturbation. For the ground state (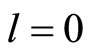 ), with respect to the time-independent perturbation theory, the change in energy for the first order is calculated as follows:
), with respect to the time-independent perturbation theory, the change in energy for the first order is calculated as follows:
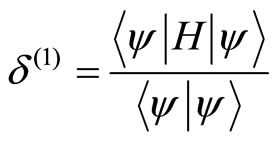 (19)
(19)
then, we have:
 (20)
(20)
where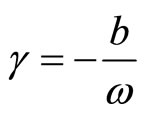 .
.
The analytic solution to the above integral is as the below form:
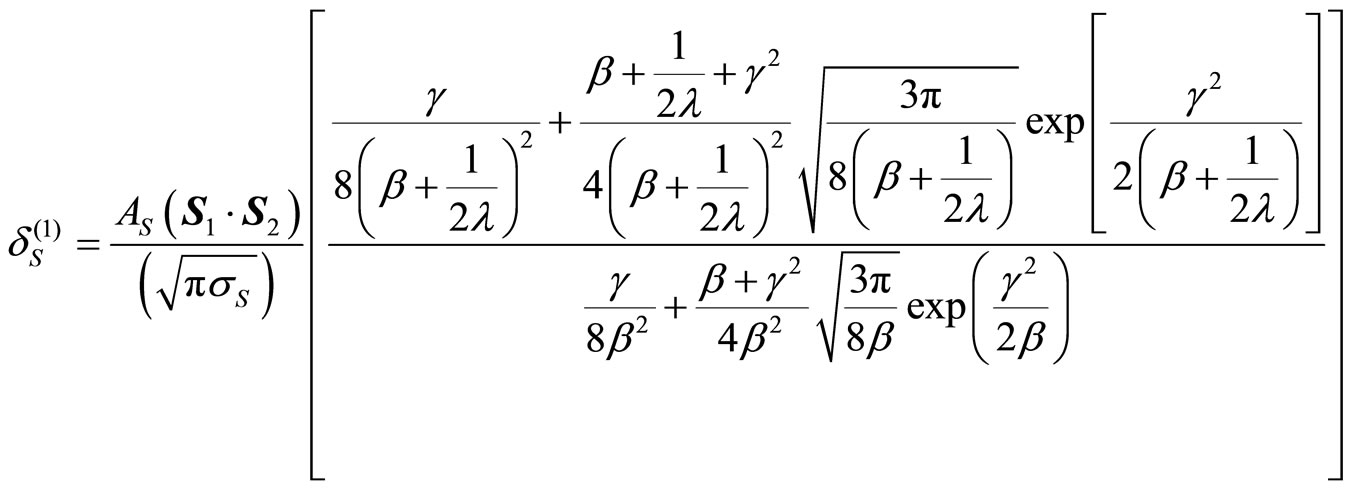 (21)
(21)
where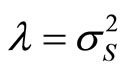 , and
, and 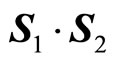 equals
equals 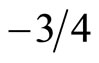 for
for , and
, and 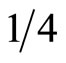 for
for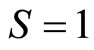 .
.
3.2. The Effect of Perturbational Potential Resulting from the Effect of Isospin-Isospin Interaction
The isospin of quark and antiquark are considered 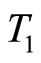 and
and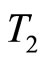 , respectively. When the distance between quark and antiquark is x, the interaction potential caused by isospin is as Equation (4). It should be noted that since merely the quarks d and u have non-zero isospin, the used mesons must possess the above quarks or corresponding antiquarks in order that the perturbation resulting from this potential term is computed. Now, if the change in energy due to the isospin-isospin contribution in the ground state (
, respectively. When the distance between quark and antiquark is x, the interaction potential caused by isospin is as Equation (4). It should be noted that since merely the quarks d and u have non-zero isospin, the used mesons must possess the above quarks or corresponding antiquarks in order that the perturbation resulting from this potential term is computed. Now, if the change in energy due to the isospin-isospin contribution in the ground state (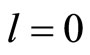 ) equals
) equals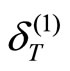 , we have:
, we have:
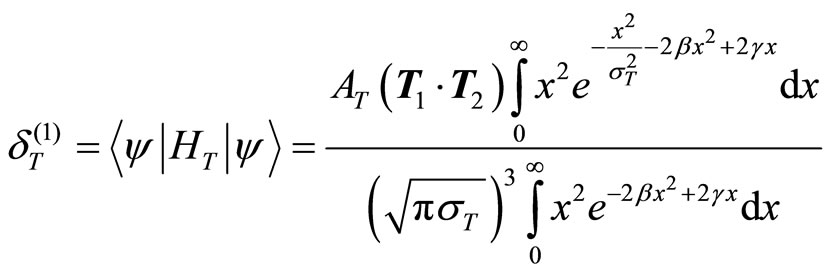 (22)
(22)
By solving the above integral:
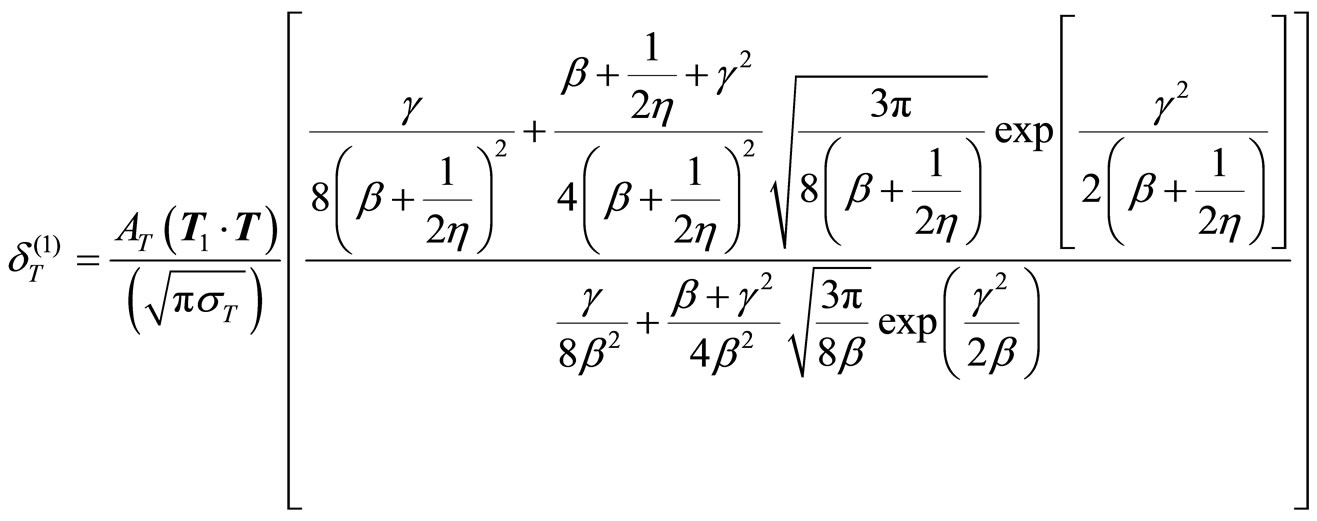 (23)
(23)
where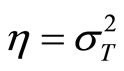 , and
, and 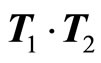 equals
equals 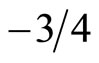 for
for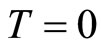 , and
, and  for
for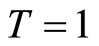 .
.
3.3. The Perturbational Potential Caused by the Effect of Spin-Isospin Interaction
The spin-isospin potential is considered as Equation (5).
The contribution of change in energy resulting from the spin-isospin effect in the ground state (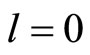 ) is denoted by
) is denoted by 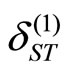 that is as follows:
that is as follows:
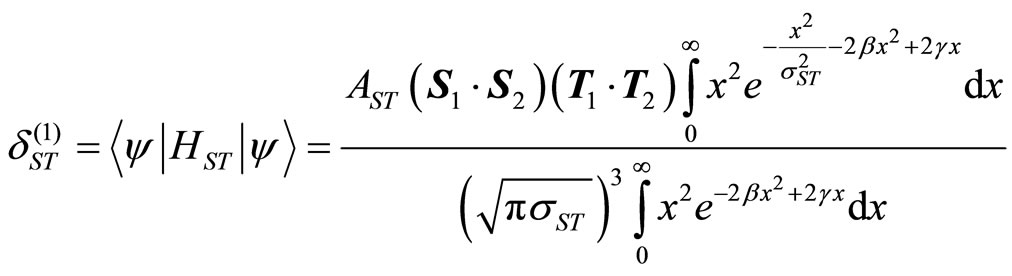 (24)
(24)
Through accurately and analytically solving the above integral:
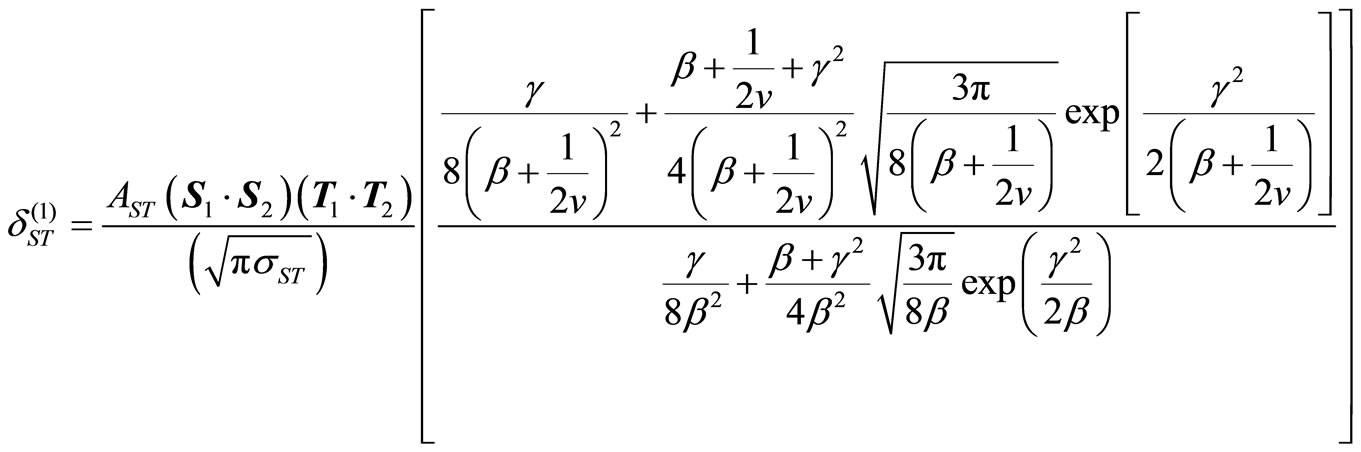 (25)
(25)
where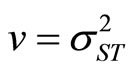 , and
, and 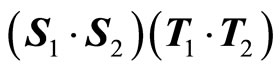 equals 9/19 for
equals 9/19 for 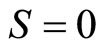 and
and , and 1/16 for
, and 1/16 for  and
and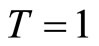 .
.
3.4. The Effects of Interaction Potential as the Perturbation in Meson Energy Commutation in the First Excited State
The mesons’ mass can also be calculated for the first excited state (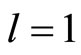 ). In this state, by considering Equations (15) and (16), the wave function and energy function are obtained as follows:
). In this state, by considering Equations (15) and (16), the wave function and energy function are obtained as follows:
 (26)
(26)
 (27)
(27)
Regarding that the mesons’ energy is considered for the first excited state, and considering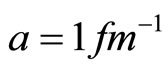 , the values of c, b, γ, β can be calculated for different mesons, and the contribution of spin-spin, isospin-isospin, and spin-isospin potentials to the energy commutation is perturbationally obtained and applied to the computation of mesons’ mass. Herein, the results achieved for the perturbation are slightly different from the ground state’s results.
, the values of c, b, γ, β can be calculated for different mesons, and the contribution of spin-spin, isospin-isospin, and spin-isospin potentials to the energy commutation is perturbationally obtained and applied to the computation of mesons’ mass. Herein, the results achieved for the perturbation are slightly different from the ground state’s results.
Based on the mass-energy equivalence and with regards to the calculated values of perturbational potentials’ terms, the meson mass can be written as follows [25-59]:
 (28)
(28)
where 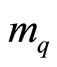 is the quark’s mass,
is the quark’s mass, 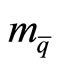 is the antiquark’s mass, and ε is the meson energy.
is the antiquark’s mass, and ε is the meson energy.
Now, through inputting the numbers obtained for the mesons with regard to the problem’s conditions to the above equation, interesting results for some of mesons’ mass in the ground or first excited states can be achieved which are provided in the tables. The theoretical results are nearly consistent with the empirical results.
4. Conclusion
Regarding Tables 1 and 2, it is observed that in what states (singlet or triplet, spin-spin or isospin-isospin) the mesons’ constituent quarks exist. For instance, in Table 1, of the meson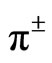 , it is observed that the spin-spin and isospin-isospin interactions are in the singlet state, and the spin-isospin interaction is in the triplet state.
, it is observed that the spin-spin and isospin-isospin interactions are in the singlet state, and the spin-isospin interaction is in the triplet state.
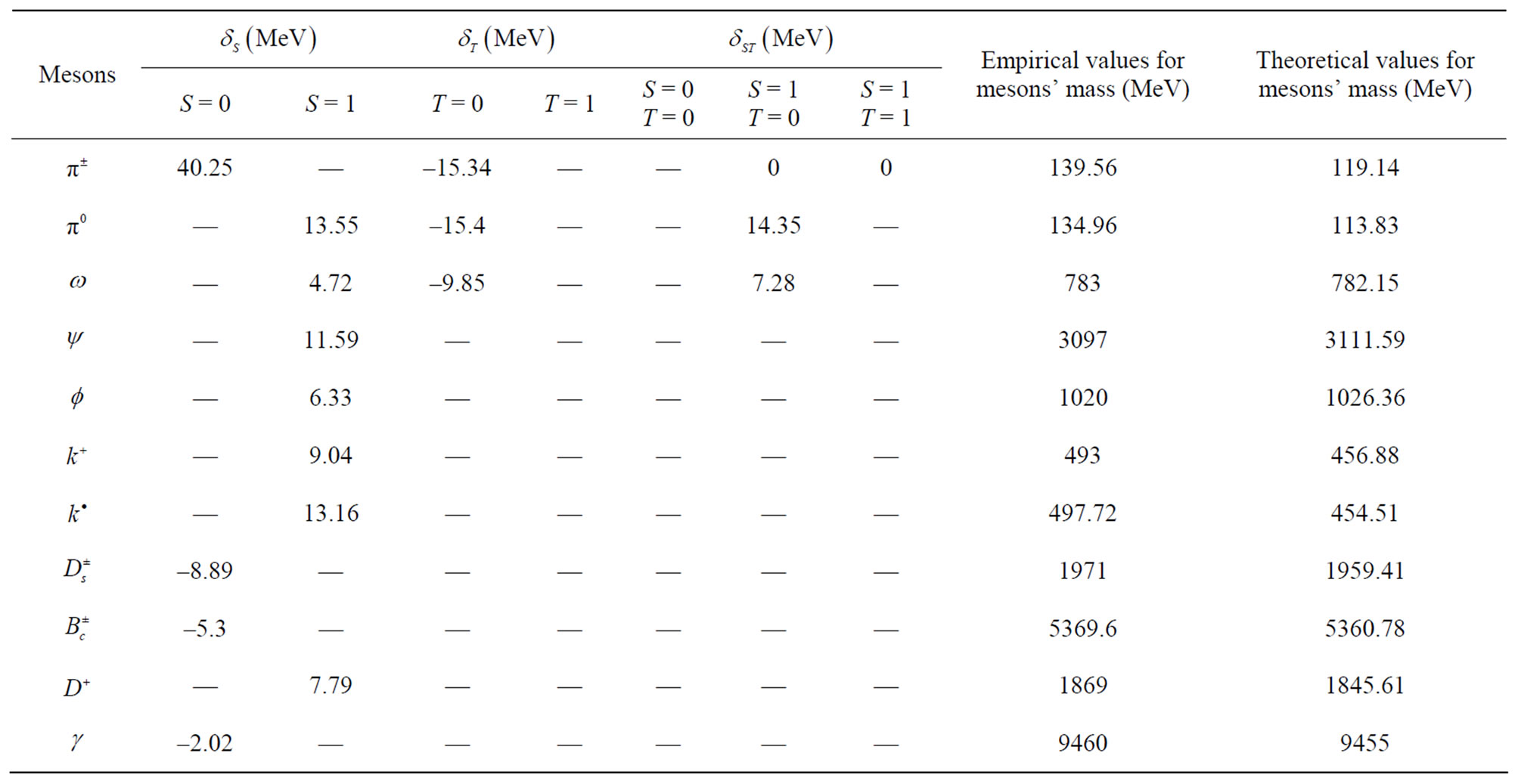
Table 1. The calculated mesons’ masses for the ground state.

Table 2. The calculated mesons’ masses for the first excited state.
5. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- N. Isgur and G. Karl, “P-Wave Baryons in the Quark Model,” Physical Review D, Vol. 18, No. 11, 1978, pp. 4187-4205. doi:10.1103/PhysRevD.18.4187
- N. Isgur, G. Karl and R. Koniuk, “Violations of SU(6) Selection Rules from Quark Hyperfine Interactions,” Physical Review Letters, Vol. 41, No. 19, 1978, pp. 1269- 1272. doi:10.1103/PhysRevLett.41.1269
- N. Isgur and G. Karl, “Symmetry Breaking in Baryons,” Physics Letters B, Vol. 74, No. 4-5, 1978, pp. 353-356. doi:10.1016/0370-2693(78)90676-7
- N. Isgur and G. Karl, “Positive-Parity Excited Baryons in a Quark Model with Hyperfine Interactions,” Physical Review D, Vol. 19, No. 9, 1979, pp. 2653-2677. doi:10.1103/PhysRevD.19.2653
- G. S. Bali, B. Bolder, N. Eicker, T. Lippert, B. Orth, P. Ueberholz, K. Schilling and T. Struckmann, “Static Potentials and Glueball Masses from QCD Simulations with Wilson Sea Quarks,” Physical Review D, Vol. 62, No. 5, 2000, pp. 054503-054515. doi:10.1103/PhysRevD.62.054503
- L. Y. Glozman and D. O. Riska, “The Spectrum of the Nucleons and the Strange Hyperons and Chiral Dynamics,” Physics Reports, Vol. 268, No. 4, 1996, pp. 263-303. doi:10.1016/0370-1573(95)00062-3
- L. Y. Glozman, W. Plessas, K. Varga and R. F. Wagenbrunn, “Unified Description of Lightand Strange-Baryon Spectra,” Physical Review D, Vol. 58, No. 9, 1998, pp. 094030-094033. doi:10.1103/PhysRevD.58.094030
- L. Y. Glozman, Z. Papp, W. Plessas, K. Varga and R. F. Wagenbrunn, “Effective Q-Q Interactions in Constituent Quark Models,” Physical Review C, Vol. 57, No. 6, 1998, pp. 3406-3413. doi:10.1103/PhysRevC.57.3406
- F. Stancu, S. Pepin and L. Y. Glozman, “How the “H Particle” Unravels the Quark Dynamics,” Physical Review D, Vol. 57, No. 7, 1998, pp. 4393-4396. doi:10.1103/PhysRevD.57.4393
- L. Y. Glozman, “Baryons in a Chiral Constituent Quark Model,” High Energy Physics—Phenomenology, Vol. 14, 1999, pp. 109-125.
- L. Y. Glozman, “Baryons, Their Interactions and the Chiral Symmetry of QCD,” Nuclear Physics A, Vol. 629, No. 1-2, 1998, pp. 121-130. doi:10.1016/S0375-9474(97)00675-1
- M. M. Giannini, E. Santopinto and A. Vassallo, “An Overview of the Hypercentral Constituent Quark Model,” Progress in Particle and Nuclear Physics, Vol. 50, No. 2, 2003, pp. 263-272. doi:10.1016/S0146-6410(03)00019-X
- M. Fabre de la Ripelle, “A Confining Potential for Quarks,” Nuclear Physics A, Vol. 497, 1989, pp. 595-602. doi:10.1016/0375-9474(89)90502-2
- M. M. Giannini, E. Santopinto and A. Vassallo, “The Hypercentral Constituent Quark Model,” Nuclear Physics A, Vol. 699, No. 1-2, 2002, pp. 308-311. doi:10.1016/S0375-9474(01)01508-1
- M. Böhm and W. Hollik, “Model Dependence of the Electromagnetic Corrections to Lepton Pair Production in Electron-Positron Collisions,” Zeitschrift für Physik C Particles and Fields, Vol. 23, 1984, pp. 31-38.
- I. M. Barbour and D. K. Ponting, “Spectroscopy and Photoproduction Couplings Using New Baryon Wavefunctions,” Zeitschrift für Physik C Particles and Fields, Vol. 4, 1980, pp. 119-129.
- A. M. Badalyan and D. I. Kitoroage, “Four-Quark States in a Potential Model,” Soviet Journal of Nuclear Physics, 1988, pp. 855-862.
- P. Geiger and N. Isgur, “Strange Hadronic Loops of the Proton: A Quark Model Calculation,” Physical Review D, Vol. 55, No. 1, 1997, pp. 299-310. doi:10.1103/PhysRevD.55.299
- P. Geiger and N. Isgur, “How the Okubo-Zweig-Iizuka Rule Evades Large Loop Corrections,” Physical Review Letters, Vol. 67, No. 9, 1991, pp. 1066-1069. doi:10.1103/PhysRevLett.67.1066
- P. Geiger and N. Isgur, “When Can Hadronic Loops Scuttle the Okubo-Zweig-Iizuka Rule?” Physical Review D, Vol. 47, No. 11, 1993, pp. 5050-5059. doi:10.1103/PhysRevD.47.5050
- P. Geiger and N. Isgur, “Quenched Approximation in the Quark Model,” Physical Review D, Vol. 41, No. 5, 1990, pp. 1595-1605. doi:10.1103/PhysRevD.41.1595
- P. Geiger and N. Isgur, “Reconciling the Okubo-ZweigIizuka Rule with Strong Pair Creation,” Physical Review D, Vol. 44, No. 3, 1991, pp. 799-808. doi:10.1103/PhysRevD.44.799
- G. S. Bali, N. Eicker, T. Lippert, H. Neff, B. Orth, K. Schilling, T. Struckmann and J. Viehoff, “Quark Mass Effects on the Topological Susceptibility in QCD,” Physical Review D, Vol. 64, No. 5, 2001, pp. 054502-054509. doi:10.1103/PhysRevD.64.054502
- G. S. Bali, “QCD Forces and Heavy Quark Bound States,” Physics Reports, Vol. 343, No. 1-2, 2001, pp. 1-136. doi:10.1016/S0370-1573(00)00079-X
- E. Eichten, I. Hinchliffe, K. Lane and C. Quigg, “Supercollider Physics,” Reviews of Modern Physics, Vol. 56, No. 4, 1984, pp. 579-707. doi:10.1103/RevModPhys.56.579
- E. Eichten, K. Gottfried, T. Kinoshita, K. D. Lane and T. M. Yan, “Charmonium: Comparison with Experiment,” Physical Review D, Vol. 21, No. 1, 1980, pp. 203-233. doi:10.1103/PhysRevD.21.203
- E. Eichten and B. Hill, “An Effective Field Theory for the Calculation of Matrix Elements Involving Heavy Quarks,” Physics Letters B, Vol. 234, No. 4, 1990, pp. 511-516. doi:10.1016/0370-2693(90)92049-O
- E. Eichten, K. Gottfried, T. Kinoshita, K. D. Lane and T. M. Yan, “Charmonium: The Model,” Physical Review D, Vol. 17, No. 11, 1978, pp. 3090-3117. doi:10.1103/PhysRevD.17.3090
- E. Eichten and F. Feinberg, “Spin-Dependent Forces in Quantum Chromodynamics,” Physical Review D, Vol. 23, 1981, pp. 2724-2744. doi:10.1103/PhysRevD.23.2724
- E. Eichten and K. Lane, “Dynamical Breaking of Weak Interaction Symmetries,” Physics Letters B, Vol. 90, No. 1-2, 1980, pp. 125-130. doi:10.1016/0370-2693(80)90065-9
- E. Eichten and K. Gottfried, “Heavy Quarks in e+e– Annihilation,” Physics Letters B, Vol. 66, 1977, pp. 286-290. doi:10.1016/0370-2693(77)90882-6
- E. Eichten and F. L. Feinberg, “Spin-Dependent Forces in Heavy-Quark Systems,” Physical Review Letters, Vol. 43, No. 17, 1979, pp. 1205-1208. doi:10.1103/PhysRevLett.43.1205
- E. Eichten and B. Hill, “Static Effective Field Theory: 1/m Corrections,” Physics Letters B, Vol. 243, No. 4, 1990, pp. 427-431. doi:10.1016/0370-2693(90)91408-4
- E. Eichten, K. Gottfried, T. Kinoshita, K. D. Lane and T.- M. Yan, “Interplay of Confinement and Decay in the Spectrum of Charmonium,” Physical Review Letters, Vol. 36, No. 10, 1976, pp. 500-504. doi:10.1103/PhysRevLett.36.500
- E. Eichten, K. Gottfried, T. Kinoshita, J. Kogut, K. D. Lane and T.-M. Yan, “Spectrum of Charmed Quark-Antiquark Bound States,” Physical Review Letters, Vol. 34, No. 6, 1975, pp. 369-372. doi:10.1103/PhysRevLett.34.369
- M. Di Pierro and E. Eichten, “Excited Heavy-Light Systems and Hadronic Transitions,” Physical Review D, Vol. 64, No. 11, 2001, pp. 114004-114023. doi:10.1103/PhysRevD.64.114004
- K. Lane and E. Eichten, “Two-Scale Technicolor,” Physics Letters B, Vol. 222, No. 2, 1989, pp. 274-280. doi:10.1016/0370-2693(89)91265-3
- E. Eichten, I. Hinchliffe, K. D. Lane and C. Quigg, “Signatures for Technicolor,” Physical Review D, Vol. 34, No. 5, 1986, pp. 1547-1566. doi:10.1103/PhysRevD.34.1547
- E. Eichten and K. Lane, “Multiscale Technicolor and Top Production,” Physics Letters B, Vol. 327, No. 1-2, 1994, pp. 129-135. doi:10.1016/0370-2693(94)91540-7
- E. Eichten, “Heavy Quarks on the Lattice,” Nuclear Physics B—Proceedings Supplements, Vol. 4, 1988, pp. 170- 177. doi:10.1016/0920-5632(88)90097-7
- K. Lane and E. Eichten, “Charm Threshold in ElectronPositron Annihilation,” Physical Review Letters, Vol. 37, No. 8, 1976, pp. 477-480. doi:10.1103/PhysRevLett.37.477
- E. Eichten and B. Hill, “Renormalization of Heavy-Light Bilinears and fB for Wilson Fermions,” Physics Letters B, Vol. 240, No. 1-2, 1990, pp. 193-199. doi:10.1016/0370-2693(90)90432-6
- E. Eichten, “ϒ Family of Resonances above Threshold,” Physical Review D, Vol. 22, No. 7, 1980, pp. 1819-1823. doi:10.1103/PhysRevD.22.1819
- E. Eichten and K. Lane, “Low-Scale Technicolor at the Tevatron,” Physics Letters B, Vol. 388, No. 4, 1996, pp. 803-807. doi:10.1016/S0370-2693(96)01211-7
- E. Eichten and J. Preskill, “Chiral Gauge Theories on the Lattice,” Nuclear Physics B, Vol. 268, No. 1, 1986, pp. 179-208. doi:10.1016/0550-3213(86)90207-5
- E. Eichten, S. Godfrey, H. Mahlke and J. L. Rosner, “Quarkonia and Their Transitions,” Reviews of Modern Physics, Vol. 80, No. 3, 2008, pp. 1161-1193. doi:10.1103/RevModPhys.80.1161
- E. Eichten, K. Lane and J. Womersley, “Finding LowScale Technicolor at Hadron Colliders,” Physics Letters B, Vol. 405, No. 3-4, 1997, pp. 305-311. doi:10.1016/S0370-2693(97)00637-0
- V. Baluni and E. Eichten, “Precocious Scaling: Evidence for Field Theory,” Physical Review Letters, Vol. 37, No. 18, 1976, pp. 1181-1184. doi:10.1103/PhysRevLett.37.1181
- E. Eichten, K. Lane and J. Womersley, “Narrow Technihadron Production at the First Muon Collider,” Physical Review Letters, Vol. 80, No. 25, 1998, pp. 5489-5492. doi:10.1103/PhysRevLett.80.5489
- N. Byers and E. E. Eichten, “Ratio of Chargedto Neutral-B-Meson Production at Υ(10580),” Physical Review D, Vol. 42, No. 11, 1990, pp. 3885-3887. doi:10.1103/PhysRevD.42.3885
- E. Eichten, G. Hockney and H. B. Thacker, “Application of Heavy-Light Methods to B Meson Physics,” Nuclear Physics B—Proceedings Supplements, Vol. 17, 1990, pp. 529-532. doi:10.1016/0920-5632(90)90307-G
- E. Eichten, R. D. Peccei, J. Preskill and D. Zeppenfeld, “Chiral Gauge Theories in the 1/N Expansion,” Nuclear Physics B, Vol. 268, 1986, pp. 161-178. doi:10.1016/0550-3213(86)90206-3
- E. Eichten and K. Lane, “Low-Scale Technicolor at the Tevatron and LHC,” Physics Letters B, Vol. 669, 2008, pp. 235-238. doi:10.1016/j.physletb.2008.09.047
- E. Eichten, “B Physics on the Lattice,” Nuclear Physics B —Proceedings Supplements, Vol. 20, 1991, pp. 475-487. doi:10.1016/0920-5632(91)90962-E
- E. Eichten and R. Jackiw, “Failure of the Eikonal Approximation for the Vertex Function in a Boson Field Theory,” Physical Review D, Vol. 4, No. 2, 1971, pp. 439-443. doi:10.1103/PhysRevD.4.439
- V. Baluni and E. Eichten, “Precocious Scaling in Field Theories,” Physical Review D, Vol. 14, No. 11, 1976, pp. 3045-3051. doi:10.1103/PhysRevD.14.3045
- A. Duncan and E. Eichten, “Improved Pseudofermion Approach for All-Point Propagators,” Physical Review D, Vol. 65, No. 11, 2002, pp. 114502-114509. doi:10.1103/PhysRevD.65.114502
- E. Eichten, K. Kang and I. G. Koh, “Anomaly-Free Complex Representations in SU(N),” Journal of Mathematical Physics, Vol. 23, No. 12, 1982, pp. 2529-2536. doi:10.1063/1.525299
- E. Eichten, G. Hockney and H. B. Thacker, “Lattice Calculation of the B-Meson Decay Constant,” Nuclear Physics B—Proceedings Supplements, Vol. 20, 1991, pp. 500-503. doi:10.1016/0920-5632(91)90965-H
NOTES
*Corresponding author.

