Journal of Modern Physics
Vol.3 No.2(2012), Article ID:17697,3 pages DOI:10.4236/jmp.2012.32025
Two Dimensional Representation of the Dirac Equation in Non-Associative Algebra
Department of Physics and Mathematics, Faculty of Sciences, Lebanese University, Beirut, Lebanon
Email: hamiehs@yahoo.fr
Received November 1, 2011; revised December 25, 2011; accepted January 6, 2012
Keywords: Dirac Equation; Non-Associative Algebra
ABSTRACT
In this note a simple extension of the complex algebra to higher dimension is proposed. Using the proposed algebra a two dimensional Dirac equation is formulated and its solution is calculated. It is found that there is a sub-algebra where the associative nature can be recovered.
1. Introduction
The physical motivation of a generalized quantum mechanics is that, although the low-energy effective theories governing the strong, electroweak, and gravitational interactions of elementary particles are believed to be described by local complex quantum field theories, attempts to construct an underlying unifying theory within the same framework have run into difficulties. Perhaps a successful unification of the fundamental forces will require one or more new ingredients at the conceptual level. One possibility, is to sacrifice the assumption of locality or of “point” particles, as is done in string theories. A second possibility, which motivates the present work, is that a successful unification of the fundamental forces will require a generalization beyond complex quantum mechanics [1-3]. The purpose, in the present paper, is to give a description of an algebra which can be used in a possible extension of the local complex quantum field theories. Also, a considerable emphasis is placed on the development of two dimensional Dirac equation. A number of interesting and characteristic features of the non associative algebra will be seen to emerge.
2. Number Systems Used in Quantum Mechanics and the Generalized-C
To determine the allowed structure of the algebra that can be used for a generalized quantum mechanics, Adler [1] introduce a number of assumptions concerning the properties of the modulus function N of the number φ element of the algebra by:
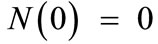 (1)
(1)
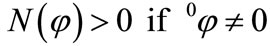 (2)
(2)
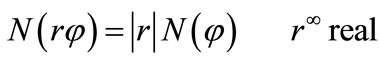 (3)
(3)
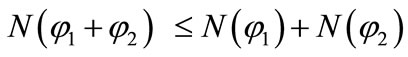 (4)
(4)
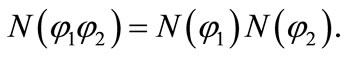 (5)
(5)
The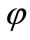 ’s are elements of a general finite dimensional algebra over the real numbers with unit element, of the form
’s are elements of a general finite dimensional algebra over the real numbers with unit element, of the form
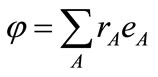
where 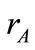 are real numbers and the
are real numbers and the 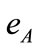 are basis elements of the algebra, obeying the multiplication law
are basis elements of the algebra, obeying the multiplication law
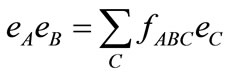
with real-number structure constants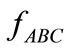 . By using the Albert theorem [4], it is found that the only algebras over the reals, admitting a modulus function N with Adler properties, are the reals R, the complex numbers C, the quaternions or Hamilton numbers H and the octonions or Cayley numbers O. However, from experimental point of view, there is no guarantee that the Adler postulate about the modulus function N will be satisfied in the new energy domains. Perhaps, new physics can emerge. Thus, there should be no restriction on the algebra that can be used for a possible extension of the complex algebra. The only requirement is that the expected extension should verify Adler postulate in its sub-algebra. Moreover, it is more natural, to assume a simple extension, rather than making extension to 4 dimensional or even higher. This idea will be used in our approach. In fact, we propose to use a three dimensional algebra. Our intuitive assumption is based on a geometrical approach as proposed by Descartes in describing the complex number.
. By using the Albert theorem [4], it is found that the only algebras over the reals, admitting a modulus function N with Adler properties, are the reals R, the complex numbers C, the quaternions or Hamilton numbers H and the octonions or Cayley numbers O. However, from experimental point of view, there is no guarantee that the Adler postulate about the modulus function N will be satisfied in the new energy domains. Perhaps, new physics can emerge. Thus, there should be no restriction on the algebra that can be used for a possible extension of the complex algebra. The only requirement is that the expected extension should verify Adler postulate in its sub-algebra. Moreover, it is more natural, to assume a simple extension, rather than making extension to 4 dimensional or even higher. This idea will be used in our approach. In fact, we propose to use a three dimensional algebra. Our intuitive assumption is based on a geometrical approach as proposed by Descartes in describing the complex number.
The proposed approach, is to generalize C algebra to the so-called Generalized-C (GC) algebra which is finitedimensional non division algebra1 containing the real numbers R as a sub-algebra and has the following properties:
A general q number in GC can be written as
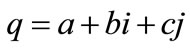
where

and the imaginary GC units, i, j are defined by
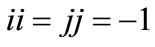
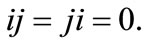
The addition of q1 and q2 in GC defined by

is associative
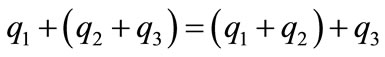
The multiplication defined by is non-associative under multiplication that is (q1 q2) q3 ≠ q1 (q2 q3).
The norm of an element q in GC is defined by
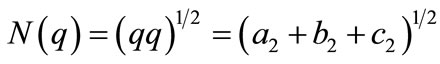
with the GC conjugate q given by
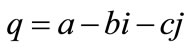 .
.
By using the previous properties of the GC, a generalization of the Euler formula to three dimension can be found. For a q in the GC, one can find the following formula
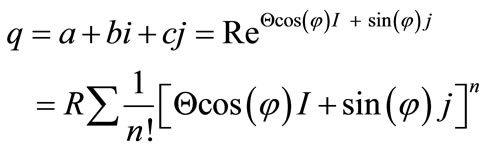
where a =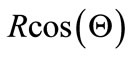 , b =
, b =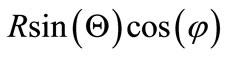 , c =
, c = 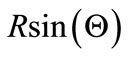
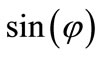 and R, Θ, φ∈R, are the distance from the origin, the polar and the azimuthal angle in the three dimension Euler space, respectively.
and R, Θ, φ∈R, are the distance from the origin, the polar and the azimuthal angle in the three dimension Euler space, respectively.
The commutativity and the non associativity of the multiplication law gives

It is essential to notify as we mention previously, that there exist a sub-algebra of GC where the probability is preserved in quantum mechanics. In this sub-algebra if we assume that the azimuthal phase φ is constant, then the GC will be an associative and division sub-algebra. We call the found sub-algebra as special GC (SGC). Hence any two numbers in this sub-algebra q1 and q2 in this sub-algebra can be written as
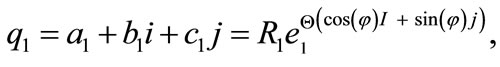
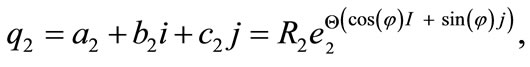
where the phase 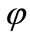 is a free parameter that can be determined from physical properties. Also, in this sub-algebra, the product of two elements have a physical meaning that is a rotation in the Euler space
is a free parameter that can be determined from physical properties. Also, in this sub-algebra, the product of two elements have a physical meaning that is a rotation in the Euler space
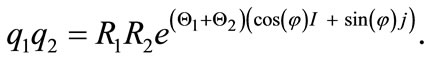
3. Two Dimensional Dirac’s Equation in the Generalized-C
This article does an ab initio development of the Dirac formalism in two dimension using the proposed Generalized-C. We know that, in C, the Dirac’s equation is often given by
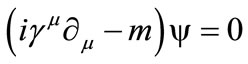
which involves i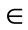 C and thus forces the first decision point in transitioning to another mathematical algebra. For clarity, to avoid the explicit use of i, the most general form (c = ħ = 1) of Dirac’s equation is
C and thus forces the first decision point in transitioning to another mathematical algebra. For clarity, to avoid the explicit use of i, the most general form (c = ħ = 1) of Dirac’s equation is
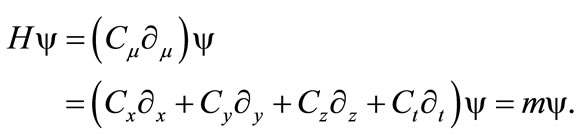 (6)
(6)
To recover the Klein-Gordon equation
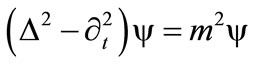 (7)
(7)
the following conditions must hold
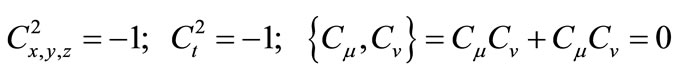 (8)
(8)
where μ ≠ ν and μ, ν = x, y, z, t. Equation (6) can be rewritten as2
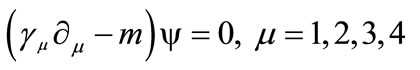 (9)
(9)
by defining
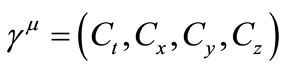
this avoids the explicit use of an imaginary scalar. Using the following Dirac matrices that take into account i, j symmetry, satisfying (8)
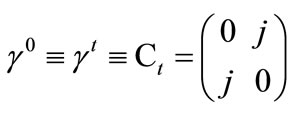
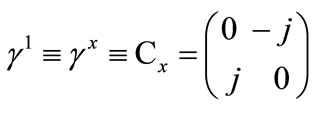
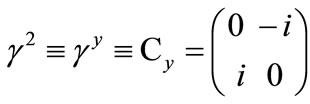
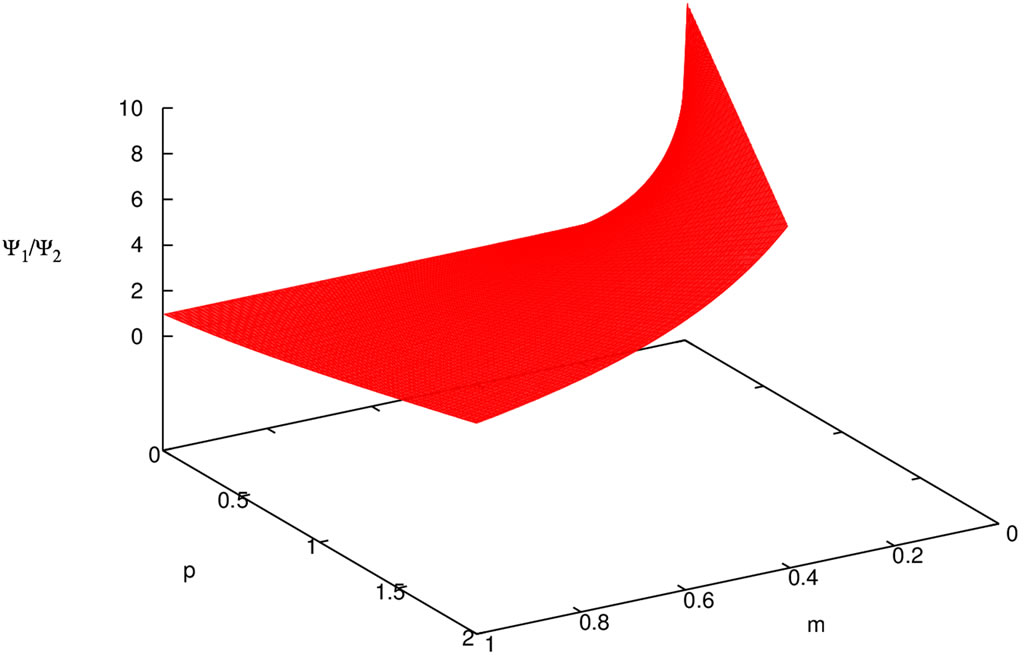
Figure 1. 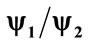 as function of m and p.
as function of m and p.
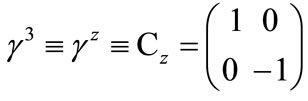
in Equation(9) we obtain
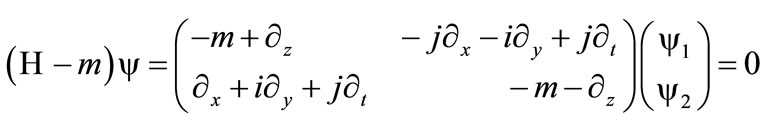 (10)
(10)
The solution to this equation in 1 + 1 dimension, x, t, is given by
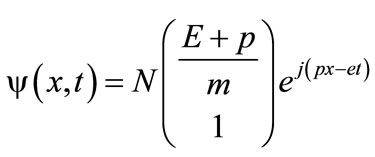 (11)
(11)
where as usual p represent the “momentum”, 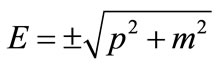 is the “energy” and N is a normalization factor. The ratio of
is the “energy” and N is a normalization factor. The ratio of 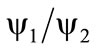 is shown in Figure 1. Discussion about the physical meaning of these results and application to local field theory will be left for future investigation.
is shown in Figure 1. Discussion about the physical meaning of these results and application to local field theory will be left for future investigation.
4. Conclusion
We have developed an algebra that extend quantum theory to new class of theories based on the non associative algebra. Also, we have found a two dimensional representation of the Dirac wave function in the non associative algebra. We believe that such algebra merit to be explored in more physical problem.
REFERENCES
- S. L. Adler, “Quaternion Quantum Mechanics and Quantum Fields,” Oxford University Press, New York, 1995.
- G. Birkhoff and J. Neuman, “The Logic of Quantum Mechanics,” Annals of Mathematics, Vol. 37, No. 4, 1936, pp. 823-843. doi:10.2307/1968621
- D. Finkelstein, J. M. Jauch, S. Schiminovich and D. Speiser, “Foundations of Quaternion Quantum Mechanics,” Journal of Mathematical Physics, Vol. 3, No. 2, 1962, pp. 207- 220. doi:10.1063/1.1703794
- A. A. Albert, “On a Certain Algebra of Quantum Mechanics,” Annals of Mathematics, Vol. 35, No. 1, 1934, pp. 65- 73. doi:10.2307/1968118
NOTES
1A division algebra, is a finite dimensional algebra for which a ≠ 0 and b ≠ 0 implies ab ≠ 0, in other words, which has no nonzero divisors of zero.
2Throughout this work the position of the indices, μ, ν etc. have no significance with respect to covariance or contravariance and are placed for typographical convenience. Repeated indices, however, do indicate summation.

