Journal of Modern Physics
Vol.3 No.6(2012), Article ID:20190,4 pages DOI:10.4236/jmp.2012.36066
Investigation and Study of the Effects of Hyperfine Interaction on the Mass of Baryons N and Δ
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani62@yahoo.com
Received October 27, 2011; revised November 12, 2011; accepted January 10, 2012
Keywords: Baryon; Spin; Isospin; Schrödinger equation; Hyperfine interaction
ABSTRACT
Constantly, providing a complete model to theoretically study baryons’ mass has been of great significance within either the relativistic range or non-relativistic range, and various potentials for theoretically modeling have been proposed. On the other hand, considering the hyperfine interactions lead to interesting results. In this paper, firstly, the hyperfine interaction and the isospin-dependent quark potential are introduced; then, the eigenfunctions and eigenvalues are nonrelativistically obtained. The results achieved for describing baryons spectrum are appropriately consistent with empirical results. The outstanding property of the model provided in this paper is that the holding potential is composed of not only a holding term with long range but also another short-range term which is a coulomb potential, and dependent on barong.
1. Introduction
Since any convincing empirical evidence for the existence of free quarks has not been observed yet, suggesting a model for theoretically investigating quarks’ mass is of great interest. The first and simplest model provided for theoretically modeling baryons’ mass is a model in which the baryon is considered to be composed of three immobile particles; and solely, the spin interaction is considered [1]. If the symmetry is full, all the octet baryons will possess an identical mass. However, as we know, the symmetry is not full. The reason is that the quark s is heavier than the quarks u and d. Also, we know that the species Σ and Δ have a relatively same mass; the mass of baryons Δ is near the proton’s mass.
The spin-spin interaction (hyperfine structure) is of great importance in the computation of baryons’ mass that its contribution to calculating baryons’ mass is considered as follows:
 (1)
(1)
where  is obtained through an appropriate processing.
is obtained through an appropriate processing.
In another model provided by Dalitz in 1967 and modified and improved by Feynman in 1968, three mobile particles with oscillating interactions are considered. Consequently, the corresponding Hamiltonian includes [2,3]:
 (2)
(2)
where , and
, and  is the relative distance between particles. Introducing the Jacobi coordinates [4-6], and not considering the particles’ rest mass, the Hamiltonian is transformed into the below form:
is the relative distance between particles. Introducing the Jacobi coordinates [4-6], and not considering the particles’ rest mass, the Hamiltonian is transformed into the below form:
 (3)
(3)
that indicates two separate oscillators with oscillation frequency of . The system’s total energy is achieved through
. The system’s total energy is achieved through  in which
in which  is the ground-state energy,
is the ground-state energy,  , and
, and [2,3]. The total angular momentum is
[2,3]. The total angular momentum is  in which
in which , and
, and . Also in this state, the parity is obtained by
. Also in this state, the parity is obtained by . The frequency
. The frequency  is achieved through the difference between the empirical masses of
is achieved through the difference between the empirical masses of  and the lowest negative parity state, and comparing it with the average mass of nucleon and
and the lowest negative parity state, and comparing it with the average mass of nucleon and . The shell P demonstrates several state of
. The shell P demonstrates several state of  with the average mass of
with the average mass of that possessing spins of
that possessing spins of ,
,  , and
, and . For the nucleon and Δ, we have
. For the nucleon and Δ, we have , and
, and ; The system’s wave function is
; The system’s wave function is [7]. Afterwardsa model has been proposed by the RGG group in 1975 [8] that are based on the below hypotheses: first, the investigation is non-relativistically performed, and there is the flavor-spin symmetry of SU (6). Second, the same as flavor, the bifurcation occurs merely through quarks’ mass. Third, the existence of holder forces with long range is independent of flavor and spin. Finally, it is assumed that the flavor-and-spin-dependent interactions with short range are only a part of the interchange of a gluon between quarks. The hyperfine interaction is considered as the below form [8]:
[7]. Afterwardsa model has been proposed by the RGG group in 1975 [8] that are based on the below hypotheses: first, the investigation is non-relativistically performed, and there is the flavor-spin symmetry of SU (6). Second, the same as flavor, the bifurcation occurs merely through quarks’ mass. Third, the existence of holder forces with long range is independent of flavor and spin. Finally, it is assumed that the flavor-and-spin-dependent interactions with short range are only a part of the interchange of a gluon between quarks. The hyperfine interaction is considered as the below form [8]:
 (4)
(4)
In this state, the baryons’ mass is as follows:
 (5)
(5)
The subtraction of nucleon’s mass from the mass of particle Δ is:
 (6)
(6)
Now, the model proposed by Isgur-Karl is considered [9]. In this Hamiltonian model, the system is defined as below:
 (7)
(7)
where
 (8)
(8)
The Isgur-Karl model’s key success in phenomenology is that the spin-orbit interaction is removed, and the spin-spin terms solely remain. When the angular momentum is zero, only, the spin-spin interaction remains in the pair of quarks; the tensor term operates when the angular momentum of quark pair is non-zero. In this state, for N = 2, there is a quintet wagon in SU (3). In fact, the elimination of the spin-orbit interaction’s term causes the baryons resonance spectrum to more approach towards empirical results to a certain extent. Despite the fact that the Isgur-Karl model desirably describes the baryons spectrum as being systematic, there are also considerable exceptions. On the other hand, it should be borne in mind that the Isgur-Karl model’s phenomenological part relates to the Isgur-Karl model of baryons lacking quark s. These results are achieved from the results of pion-nucleon scattering and investigation of properties of particles synthesized in this scattering. The Isgur-Karl model predicts more states in comparison to what is really observed.
2. The Precise Solution to the Radial Schrödinger Equation for Determining Baryons’ Mass
Using the hyperspherical coordinates, the kinetic energy operator for a three-body ensemble is written as the below form ( ) [10].
) [10].
 (9)
(9)
The eigenfunctions of  are hyperspherical harmonics that are as follows:
are hyperspherical harmonics that are as follows:
 (10)
(10)
The eigenvalue of large angular momentum (γ) equals  where
where . Moreover,
. Moreover,  and
and  are the corresponding momentum of
are the corresponding momentum of  and
and  quantities, respectively. On the other hand, every threebody state can be expanded according to hyperspherical harmonics.
quantities, respectively. On the other hand, every threebody state can be expanded according to hyperspherical harmonics.
 (11)
(11)
The hyper-radial wave function 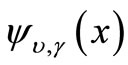 is a solution of the below radial Schrödinger equation:
is a solution of the below radial Schrödinger equation:
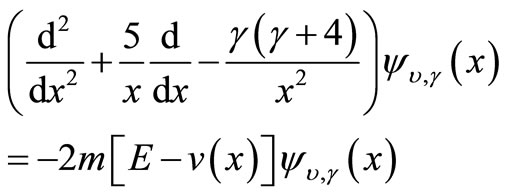 (12)
(12)
Now, the hyper-radial Schrödinger equation is solved for the three-body interaction potential. In this regard, the below transform is considered:
 (13)
(13)
After lengthy calculations for , the eigenvalues and eigenfunctions are obtained as the following forms [11]:
, the eigenvalues and eigenfunctions are obtained as the following forms [11]:
 (14)
(14)
 (15)
(15)
and for , the eigenvalues and eigenfunctions are as follows [11]:
, the eigenvalues and eigenfunctions are as follows [11]:
 (16)
(16)
 (17)
(17)
Therefore, each baryon’s energy is achieved through the equation obtained for  which is a function of a, b, and
which is a function of a, b, and . In this stage, the potential corresponding to hyperfine interactions
. In this stage, the potential corresponding to hyperfine interactions  is considered as perturbation [12]. The perturbed wave function
is considered as perturbation [12]. The perturbed wave function  for all the states can be written as below:
for all the states can be written as below:
 (18)
(18)
and the contribution of hyperfine-interactions potential is acquired using the following equation:
 (19)
(19)
Certainly, the higher orders of this energy contribution can be computed through utilizing this method. The baryon’s mass is written as follows [13]:
 (20)
(20)
This dependency for constitutive-quarks model is dependent upon quark’s mass ( ), and the coefficients of potential a and b.
), and the coefficients of potential a and b.  and
and  are the angular momentum and counter of radial wave function
are the angular momentum and counter of radial wave function , respectively. The masses considered for quarks include md = 360 (Mev), mu = 257 (Mev), and ms = 501.5 (Mev).
, respectively. The masses considered for quarks include md = 360 (Mev), mu = 257 (Mev), and ms = 501.5 (Mev).
The information on baryons Ʌ and Δ containing either short ranges or long ranges are utilized to achieve the coefficients of potential. For this purpose, Ʌ (1232) and Δ(1672) are used as inputs for determining the coefficients of potential a, b, and c. In this state, ,
, ,
, ,
, . Based on this model and considering hyperfine effects, the theoretical and empirical values of baryons’ mass are mentioned in Tables 1 and 2.
. Based on this model and considering hyperfine effects, the theoretical and empirical values of baryons’ mass are mentioned in Tables 1 and 2.
3. Conclusion
Many theoretical efforts to calculate baryons’ mass in the presence of a holding potential have been made, and most of baryonic spectrum is described through different constituent quark models (CQM). Nevertheless, the accuracy of constituent quark model (CQM) to describe hadrons’ masses is a controversial issue. However, within

Table 1. The empirical and theoretical masses of family N.

Table 2. The empirical and theoretical masses of family Δ.
within the range this model is valid, exploiting it brings about acceptable results. The outstanding feature of the model provided in this paper is that the holding potential is composed of not only a holding term with long range but also another short-range term which is a coulomb potential, and dependent on barong. On the other hand, the interquark potentials are dependent on flavor, and contain the terms depending on spin , isospin
, isospin , and spin-isospin
, and spin-isospin  that are of great importance. In this paper, these terms’ effects are computed in the framework of the proposed model.
that are of great importance. In this paper, these terms’ effects are computed in the framework of the proposed model.
4. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- A. B. Volkov, “Equilibrium Deformation Calculations of the Ground State Energies of 1p Shell Nuclei,” Nuclear Physics, Vol. 74, No. 1, 1965, pp. 33-58. doi:10.1016/0029-5582(65)90244-0
- R. P. Feynman, “Very High-Energy Collisions of Hadrons,” Physical Review Letters, Vol. 23, No. 24, 1969, pp. 1415-1417. doi:10.1103/PhysRevLett.23.1415
- R. P. Feynman, “Photon-Hadron Interactions,” Addison-Wesley, New York, 1972.
- A. J. Dragt, “Classification of Three—Particle States According to SU3,” Journal of Mathematical Physics, Vol. 6, No. 4, 1965, pp. 533-553. doi:10.1063/1.1704306
- A. J. Dragt, “Relativistic Three—Particle SU3 States,” Journal of Mathematical Physics, Vol. 6, No. 11, 1965, pp. 1621-1625. doi:10.1063/1.1704703
- J. L. Ballot, M. Fabre de la Ripelle and J. S. Levinger, “Coupled Adiabatic Approximation in the Three-Body Problem,” Physical Review C, Vol. 26, No. 5, 1982, pp. 2301-2309. doi:10.1103/PhysRevC.26.2301
- T. R. Schneider, “Convergence of Generalized Spherical Harmonic Expansions in the Three Nucleon Bound State,” Physics Letters B, Vol. 40, No. 4, 1972, pp. 439- 442. doi:10.1016/0370-2693(72)90545-X
- A. W. Thomas and W. Weise, “The Structure of the Nucleon,” WILEY-VCH Verlag Berlin GmbH, Berlin, 2005.
- A. De Rújula, H. Georgi and S. L. Glashow, “Hadron Masses in a Gauge Theory,” Physical Review D, Vol. 12, No. 1, 1975, pp. 147-162. doi:10.1103/PhysRevD.12.147
- H. Leeb, H. Fiedeldey, S. A. Sofianos, R. Lipperheide and M. F. de la Ripelle, “Nonrelativistic Quark-Antiquark Potential for Mesons,” Nuclear Physics A, 1990, Vol. 508, pp. 365-370. doi:10.1016/0375-9474(90)90499-C
- N. Isgur and G. Karl, “P-Wave Baryons in the Quark Model,” Physical Review D, Vol. 18, No. 11, 1978, pp. 4187-4205. doi:10.1103/PhysRevD.18.4187
- M. F. de la Ripelle, “A Confining Potential for Quarks,” Nuclear Physics A, Vol. 497, 1989, pp. 595-602. doi:10.1016/0375-9474(89)90502-2
- M. M. Giannini, E. Santopinto and A. Vassallo, “An Overview of the Hypercentral Constituent Quark Model,” Progress in Particle and Nuclear Physics, Vol. 50, No. 2, 2003, pp. 263-272. doi:10.1016/S0146-6410(03)00019-X
NOTES
*Corresponding author.

